认知无线电线性自信号消除带内频谱感知方法

刘 超,孙雁飞

(1.南京邮电大学 信息网络技术研究所,南京 210003;2.江苏大学电气信息工程学院,江苏 镇江 212013)

1 引 言

认知无线电(Cognitive Radio,CR)通过无线环境感知已经固定分配给授权用户(首要用户)的频段以及其它空闲频段[1]。根据感知目的的不同,对主用户信号检测可以分为两种类型:带外检测和带内检测[2]。带内检测需要避免来自自身网络内部通信的干扰,目前主要有两种方法[3]:一是基于静默期的带内检测,通过抑制网络中所有用户在带内检测期间的发射活动来避免网络自身通信的干扰,但静默期将导致通信的短暂中断,引入了额外的开销;二是基于动态跳频的带内检测,以其它空闲信道为中介,将当前工作频段调整到空闲信道,实现从带内感知到带外感知的转化。该方法在一定程度上可以保持通信的连续性,但需要借助于额外的信道,造成无线资源的浪费。针对上述已有带内检测方法的不足,文献[4]提出了基于信道估计的带内感知算法,借助信道估计的结果和解调信号对接收到的自身信号进行重建,再将接收到的信号减去重建后的信号,从而实现自信号抑制。但是该方法实现复杂度相对较高,性能受信道估计和误码率影响明显。

本文提出了一种基于线性自信号消除的带内信号检测方法。该方法利用了无线衰落信道AR模型,通过对相邻接收符号进行线性加权,消除接收信号中的自信号。同时给出了奈曼-皮尔逊准则下最优检测器,用于在自信号消除后的剩余信号上进行频谱感知。对算法进行了性能分析,仿真表明,本文方法能够达到和利用静默期的能量检测相近的性能,满足IEEE 802.22系统的检测要求。

2 系统模型

传统的频谱感知方法中,由于静默期的存在,检测器接收到的信号中不包含次用户自身网络的信号。当主用户信号出现时,接收信号y(n)可以表示为

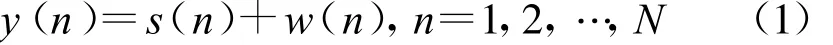
式中,n表示第n个接收信号的样点,s(n)表示接收到的主用户信号,主用户信号受到本地的零均值复高斯加性白噪声w(n)的干扰。假设w(n)的方差为 δ2w,噪声过程是平稳的,文献[5]表明,当s(n)信号样点间存在相关性时,如多径信道的记忆效应,可以获得更好的检测性能。

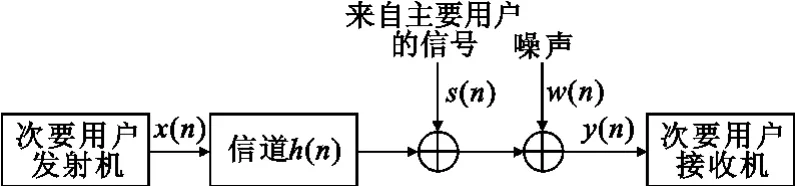
图1 系统模型Fig.1 System model

如图1所示,这里考虑认知无线电网络中的一对次用户的发射机和接收机。当检测过程中不存在静默期时,公式(1)所示的接收信号y(n)将进一步混叠自信号。平坦衰落信道下,有:

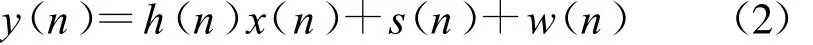
式中,h(n)x(n)为自信号,h(n)为信道增益。为了保证不对主用户造成干扰,次用户必须能够检测极弱的主用户信号。如在IEEE 802.22无线区域网中,要求能够检测到-116dBm(SNR=-22dB)的电视信号[6,7]。鉴于低信噪比下信号检测的要求,这里假设主用户信号s(n)要低于噪声w(n)。因此认为次用户可以通过解调获得x(n)的值,而当x(n)是前导序列时,其取值也是已知的。

根据是否出现主用户的信号,公式(2)下的主用户信号检测问题可以表示为以下二元假设检验:

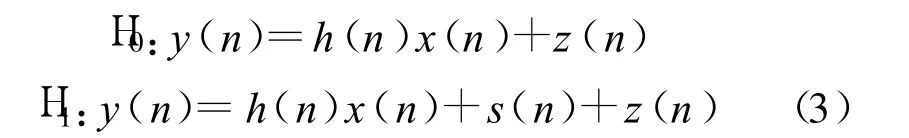
式中,Η0表示主用户不存在,Η1则表示存在主用户的情况。

如果直接运用传统的检测方法,次用户自信号h(n)x(n)的存在会对检测性能造成负面的影响,检测性能随次用户信号功率的提高而恶化。后续的仿真结果说明了该问题。

3 基于信道特征的线性自信号消除

利用自信号消除的方法消去自信号时,自信号消除后的残差信号可以由另一个复高斯随机变量r(n)表示。经历自信号消除后,假设检验变为

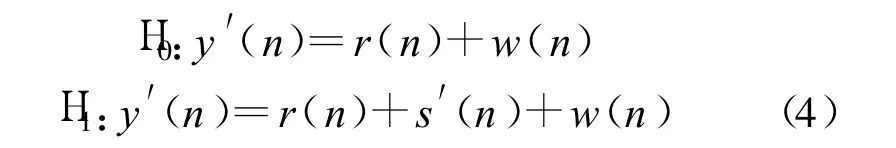
一般意义上可以认为r(n)越小,自信号消除的效果越好,自信号消除后的残余信号对检测性能的影响就越小。

3.1 线性自信号消除

考虑到信道因相关性引入的记忆效应,衰落信道模型可以由一阶AR模型表示[8]:

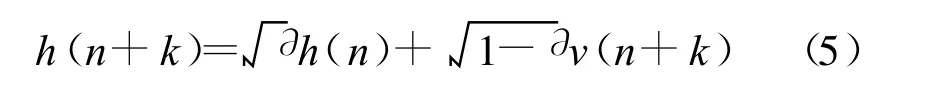
式中,v(n+k)是与h(n)独立同分布的零均值复高斯随机变量,各样点对应的v(n+k)也是相互独立的。上式中,由陆地移动衰落信道的Jakes模型[9]得到

式中,JO(·)表示第一类零修正阶贝塞尔函数;f=fdTs,其中fd表示最大多普勒频移,Ts为采样周期。

由公式(5)可知,样点间距越小其信道相关性越强。公式(7)给出了本文提出的基于相邻样点符号的线性加权自信号消除(LSSE)的表达式:

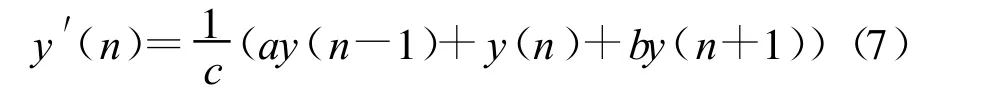
注意到w(n-1)、w(n)和w(n+1)为独立同分布复高斯随机变量,公式(7)括号中的部分依概率可表示为

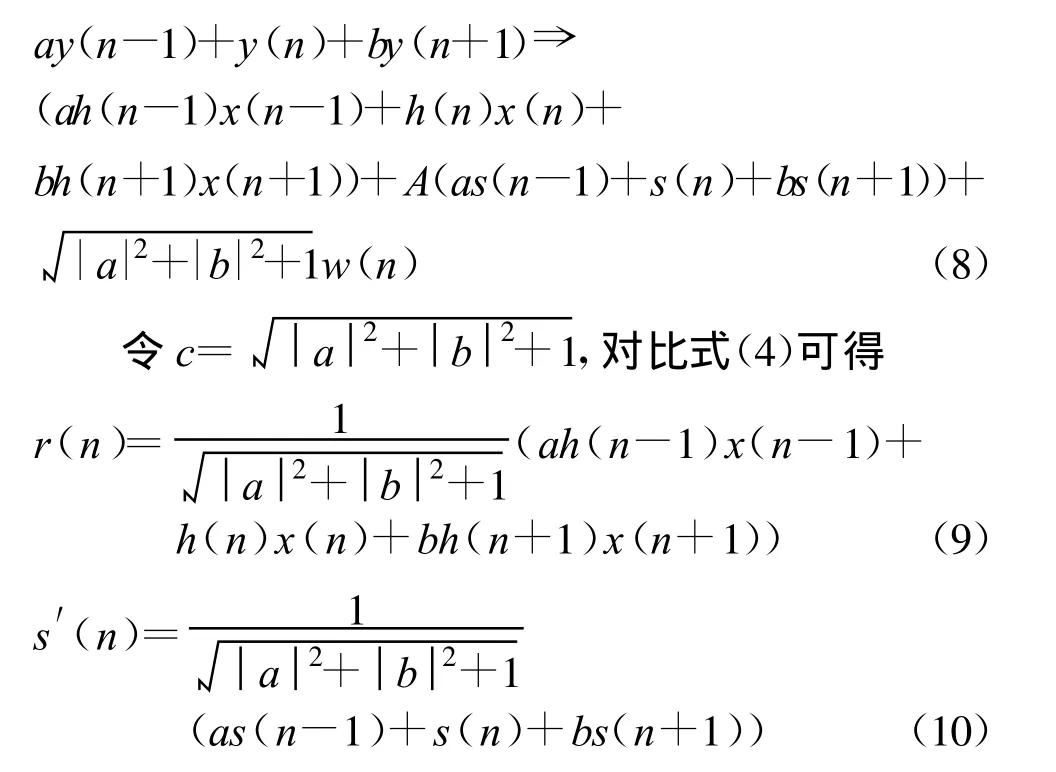
将公式(5)的对应关系代入到公式(9)中,求解a和b,令r(n)方差最小,即残差的自信号的能量最小。通过推导可得

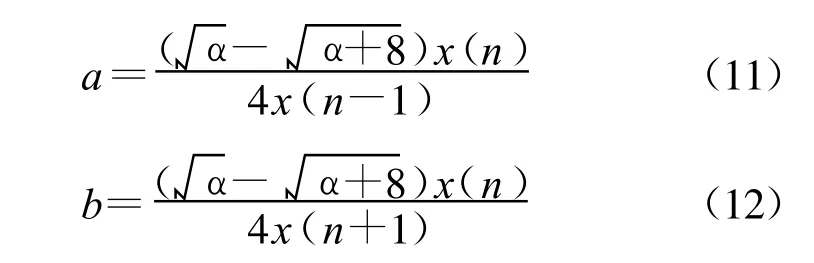
最终,得到的线性加权自信号消除方法为

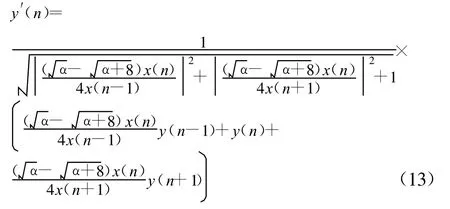
3.2 最佳检测器

将公式(4)的假设检验表示为矢量形式:

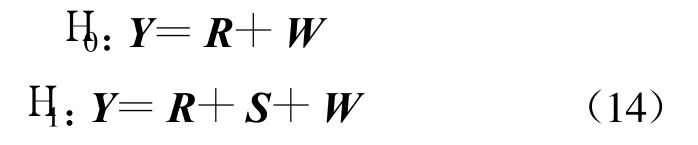
式中,Y=[y′(1),…,y′(N)]T,R=[r(1),…,r(N)]T,W=[w(1),…,w(N)]T和 S=[s′(1),…,s′(N)]T。噪声 W的协方差矩阵为同时假设H(X)=[h(1)x(1),…,h(N)x(N)]T的协方差矩阵为CX,则可以根据公式(9)计算 CR。理想情况下,即相邻符号间信道不发生变化的情况,CR=0,可将自信号完全消除。

在Bayes(贝叶斯)准则下,通常难以为各种决策确定相应的代价,因此在实际的检测过程中将采用奈曼-皮尔逊准则。基于检验假设公式(14),线性自信号消除为基础的最优检测器由以下似然比表示为

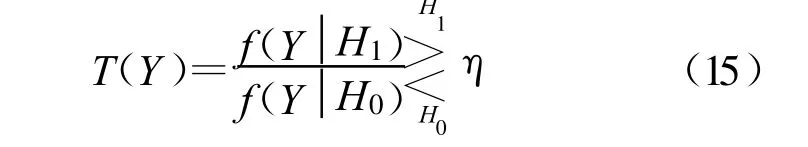
判决符号左侧为似然比,右侧为根据虚警概率Pf确定的最优判决门限η。

当s(n)未知时,经历衰落信道后主用户信号s(n)可以视为独立同分布复高斯随机变量。S的协方差矩阵可以表示为CS,此时:

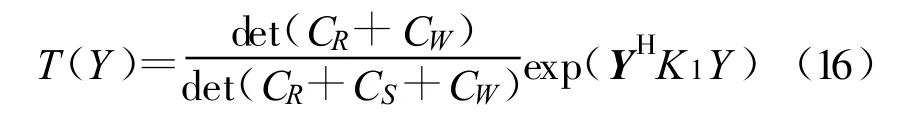
其中K1=(CR+CW)-1-(CR+CS+CW)-1。

根据公式(15),两端取自然对数并整理,似然比可以表示为

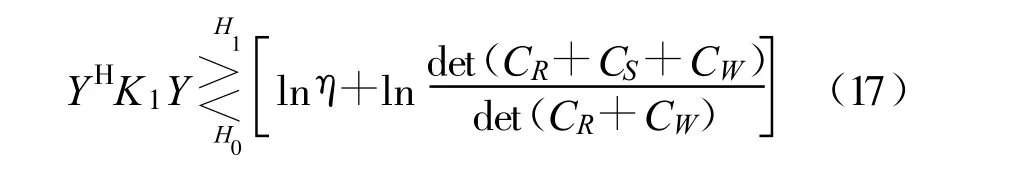
YHY表示向量Y的能量,因此YHK1Y可视作加权能量,其中 K1为加权矩阵。该检测器的性能难以给出解析表达。当s(n)已知时,

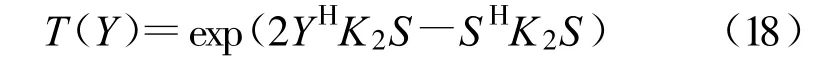
其中K2=(CR+CW)-1。根据公式(15),两端取自然对数并整理,似然比可以表示为

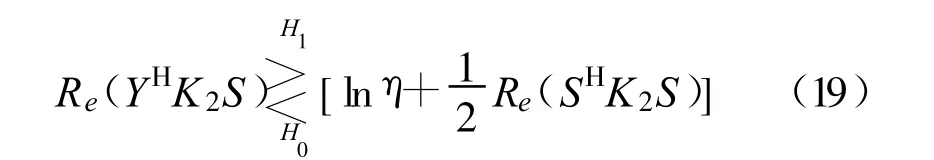
3.3 算法总结

以上讨论了基于线性自信号消除的带内频谱感知方法的主要内容及分析,算法流程具体描述如下:

(1)接收N+2个连续符号y(0),y(1),…,y(N+1);

(2)利用公式(13)进行自信号消除,获得消除后信号矢量为 Y=[y′(1),y′(2),…,y′(N)]T;

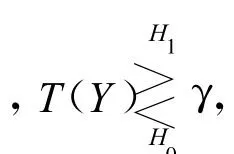
4 性能仿真

通过仿真对本文提出的基于线性自信号消除的频谱感知方法的性能进行衡量。仿真中,信道使用了IEEE 802.22无线区域网标准工作组所定义的信道模型[9],如表1所示。采样速率为6×8/7MHz。

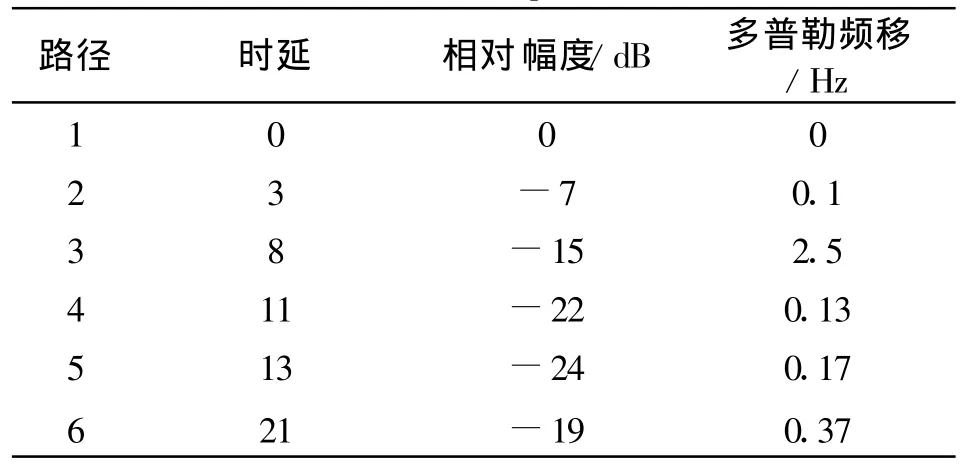
表1 信道参数表Table 1 Channel parameters

为方便叙述,定义信噪比(SNR)和干噪比(INR)如下:

进行1000次蒙特卡洛仿真。除本节提出的LSSE方法外,同时给出了采用文献[10]中基于互补符号对(Complementary Symbol Couples,CSC)的自信号消除方法和不采用自信号消除的能量检测(Without LSSE ED)的性能曲线。LSSE ED为本文方法 s(n)未知时的检测性能曲线,LSSE MD为s(n)已知时的性能曲线。

4.1 INR对检测性能的影响

接收机工作特性曲线(ROC)是奈曼皮尔逊准则下衡量检测性能的常用方法。图2给出了SNR=10dB时不同INR下的ROC对比。从图2中可以看出,INR对检测性能有很大的影响,LSSE在s(n)已知时的性能明显优于其它3种情况,而LSSE ED的性能与文献[10]中所示方法基本相当。INR为-16dB、虚警概率 Pf为0.1的情况下,检测概率Pd均大于0.85。

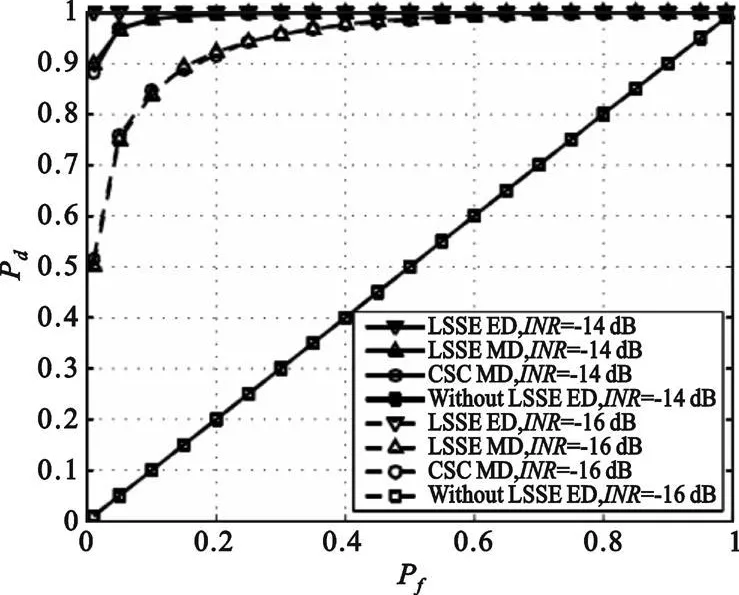
图2 不同INR下检测性能对比Fig.2 Detection performance comparison of different INR

4.2 SNR对检测性能的影响

受信道变化影响,自信号消除并不能完全消除自身信号,因此信号残差也与自信号有关。图3给出了自信号功率对检测性能的影响,其中点线和实线给出了SNR=10dB和SNR=20dB时的ROC性能曲线。可以看出在不同的SNR情况下,两种曲线基本重合,也就是说次用户自信号对检测性能影响很小。因此本文方法是一种性能较稳定的主用户信号检测方法。

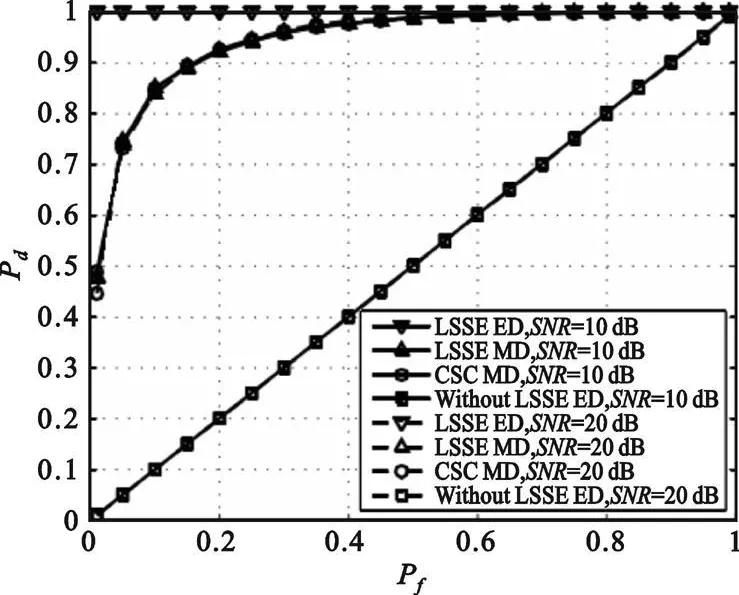
图3 不同SNR下检测性能的对比Fig.3 Detection performance comparison of different SNR

4.3 信道相关性对检测性能的影响

公式(6)中,α由多普勒频移决定,因此多普勒频移越小,相应的自信号消除的性能越好。在IEEE 802.22无线区域网环境下多普勒频移较小,因此本文方法的性能与CSC方法具有相近的检测性能,如图2和图3所示。由于自信号消除后的残差与信道相关系数α有关,在图4的分析中,我们将展示在具有较大多普勒频移(α较小)的情况下,本文方法要优于CSC方法。

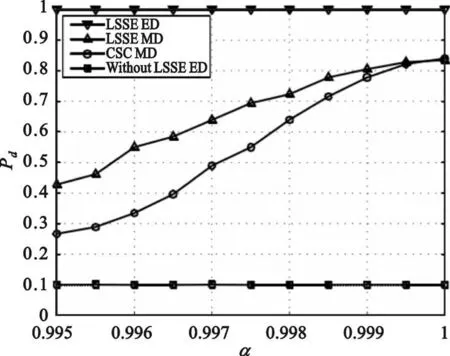
图4 α对检测性能的影响Fig.4 Impaction of αon the detection performance

图4给出了不同 α下的采用检测的性能曲线。仿真中INR=-16dB,SNR=10dB,并且保持虚警概率Pf=0.1。由图4可以看出,本文所提出的自信号消除方法在已知s(n)和未知s(n)时在相同 α下的性能均优于文献[10]中方法,而s(n)已知情况下的检测性能要优于s(n)未知时的检测性能,符合检测理论常识。

5 结束语

本文提出了一种基于线性自信号消除的认知无线电带内频谱感知方法。该方法利用无线衰落信道AR模型,通过对相邻接收符号进行线性加权,消除接收信号中的自信号。同时给出了奈曼-皮尔逊准则下最优检测器,用于对自信号消除后的剩余信号进行频谱感知。仿真结果表明,本文提出的方法在多普勒频移较大时优于已有的无静默期带内频谱感知方法。

[1] Kolodzy P J.Interference temperature:a metric for dynamic spectrum utilization[J].International Journal of Network Management,2006,16(2):103-113.

[2] William Krenik,Anuj Batra.Cognitive radio techniques for wide area network[C]//Proceedings of the 42nd Annual Design Automation Conference.New York,USA:ACM,2005:409-412.

[3] IEEE P802.221.22TM/D0.1,Draft Standard for Wireless Regional Area Networks Part 22:Cognitive Wireless RAN Medium Access Control(MAC)and Physical Layer(PHY)specifications:Policies and procedures for operation in the TV Bands[S].

[4] Ji Baowei,Din Yingong,Mazzarese D.Channel sensing based on self-signal suppression(SSS)[EB/OL].2006-07-14[2011-04-26].http://www.ieee802.org/22/Meetingdocuments/2006/July/22-06-0120-00-0000SamsungSSS-BasedChannelSensing.doc.

[5] Tang H.Some physical layer issues of wide-band cognitive radio systems[C]//Proceedings of the First IEEE International Symposium on New Frontiers in dynamic Spectrum Access Networks.Baltimore,MD,USA:IEEE,2005:151-159.

[6] IEEE std.802.22-06/0088r0,Numerical spectrum sensing requirements[S].

[7] IEEE std.802.22-05/0007r46,Functional requirements for the 802.22wran standard[S].

[8] Peel C,Swindlehurst A.Effective SNR for space-time modulation over a time-varying rician channel[J].IEEE Transactions on Communications,2008,52(1):17-23.

[9] Jakes W C,Cox D C.Microwave mobile communications[M].New York:Wiley,1974:225-226.

[10] Chen D,Li J,Ma J.In-band sensing without quiet period in cognitive radio[C]//Proceedings of 2008 IEEE International Conference on Wireless Communications and Networking.LasVegas,NA:IEEE,2008:723-728.