无网格局部Petrov-Galerkin法分析板弯曲的剪切自锁问题

夏 平,胡玮军,程玉兰

(1.湖南工程学院机械工程学院,湘潭 411101;2.邵阳学院机械与能源工程系,邵阳 422000)

无网格局部Petrov-Galerkin法分析板弯曲的剪切自锁问题

夏 平1,胡玮军2,程玉兰1

(1.湖南工程学院机械工程学院,湘潭 411101;2.邵阳学院机械与能源工程系,邵阳 422000)

用径向基函数构造无网格局部Petrov-Galerkin方法的形函数,插值函数具有Kronecker delta函数性质,因此可以很方便地施加本质边界条件.分析了板弯曲时剪切自锁现象产生的原因,利用无网格局部Petrov-Galerkin方法对两对边固支另对边简支中厚板的弯曲进行了分析和计算.发现无网格方法相对于有限元法等传统数值方法能更好地避免剪切锁死现象,并提出了避免剪切自锁现象发生的有效措施.

无网格局部Petrov-Galerkin方法;径向基函数;弯曲问题;剪切自锁

0 引 言

无网格方法是一类在有限元法等传统数值方法基础上,针对其网格单元存在的问题而提出的一类新的数值方法.无网格方法目前已有数十种之多[1,2],其中无网格Garlerkin法[3]和无网格Petrov-Garlerkin法[4]是最常用的两种无网格方法.

无网格方法是基于节点信息而不是基于单元或网格信息,因此有利于避免剪切自锁问题.用有限元法求解薄板问题时,常常会在板很薄的情况下发生剪切锁死现象,于是采用一系列的方法来避免剪切自锁现象的发生,如缩减积分法和假设剪切应变方法等[5].本文通过用无网格局部Petrov-Garlerkin法对中厚板的弯曲进行计算来对剪切自锁问题进行分析.

1 中厚板的基本方程

在图1所示笛卡尔坐标系中,取 xy为板的中面,取z轴与xy面垂直向下,设板厚度为h,x和y方向的长度分别为a,b.板内任一点在变形后沿 x,y,z轴方向的位移分量记为u,v和w,用三个广义位移 θx(x,y),θy(x,y),w(x,y)来表示三个位移分量,存在关系

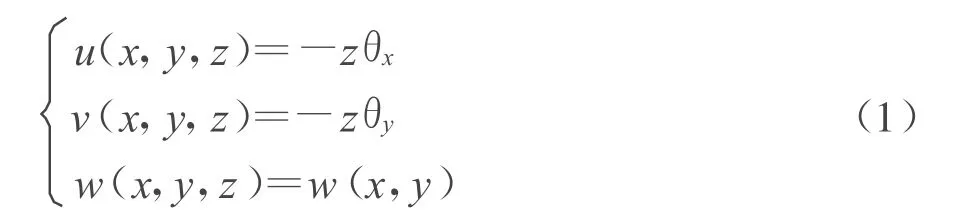
其中θx、θy分别是垂直中面的直法线在xz和yz平面内的转角,w(x,y)为中面挠度.轴向位移和角位移的正方向如图1所示.

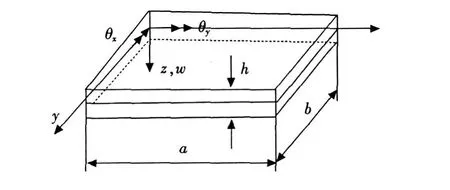
图1 矩形板

对于各向同性板,广义内力与广义应变之间的关系形式上可以表示为

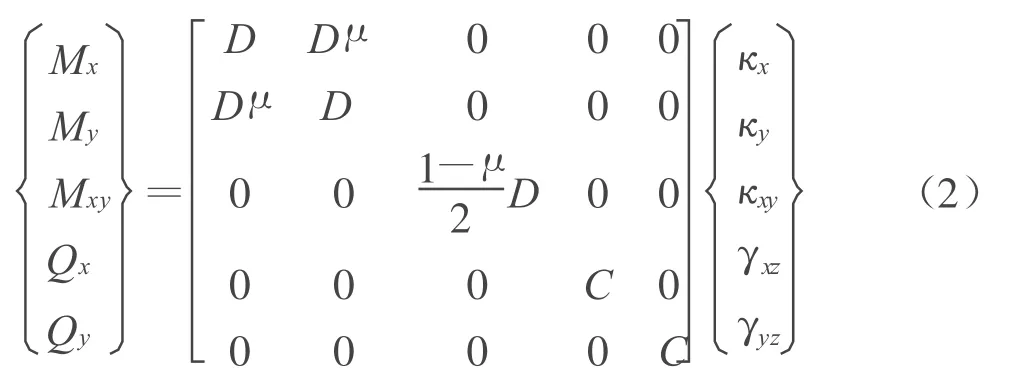
或

式中,σ为广义内力向量

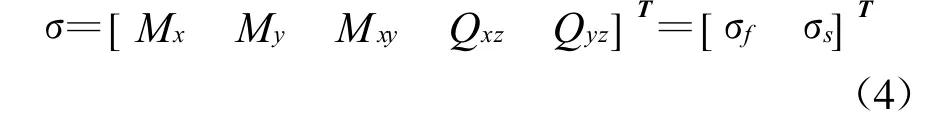
ε为广义应变向量

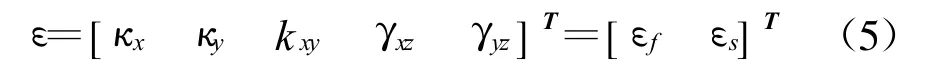
其中,εf为弯曲应变向量,εs为剪切应变向量

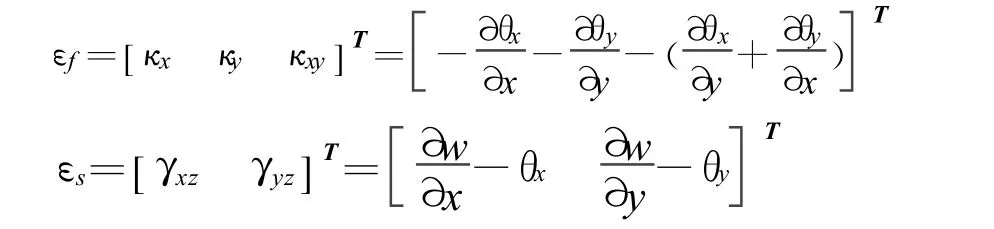
在式(3)中,D为板材料的弹性矩阵

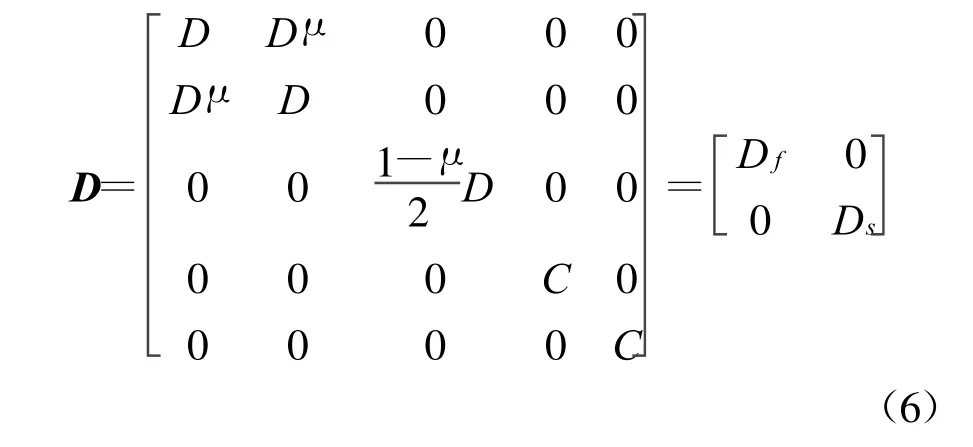
其中D为板的弯曲刚度,C为板的剪切刚度.

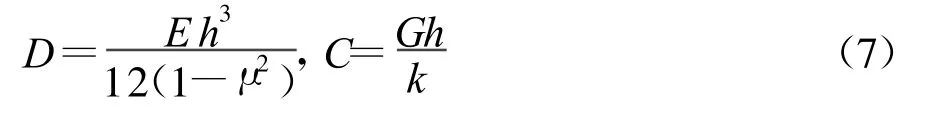
式中,E、G和μ分别为板材料的弹性模量、剪切模量和泊松比.

2 剪切自锁产生的原因

中厚板的应变能包括弯曲应变能和剪切应变能两部分.由中厚板的虚功原理,即弯曲虚应变能和剪切虚应变能之和等于外载荷的虚功可得

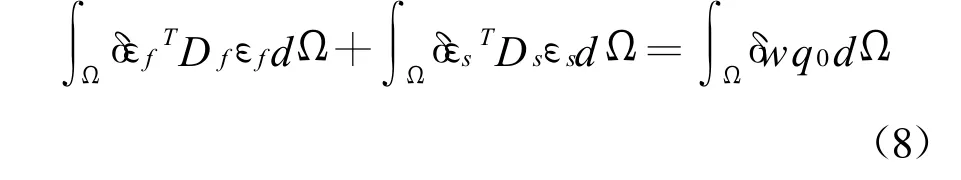
当板变得比较薄的时候,方程(8)左边的第二项即与剪切应变相关的剪切应变能项可能变得比与第一项弯曲应变相关的弯曲应变能大.在数值模拟中,都使用同阶多项式函数近似位移变量w、θx和θy,因此当板变得很薄时,第二项会变得比第一项大很多,这样就会导致出现错误的结果,这种现象称为剪切自锁.有限元法中一般使用线性函数来插值位移变量 w 、θx和θy,由于 ∂w/∂x与 ∂w/∂y和 θy与 的阶次不协调,剪切应变能比弯曲应变能大很多,这时就很容易导致剪切自锁现象的发生.

3 避免剪切自锁现象的有效措施

3.1 采用高次多项式基函数

在无网格局部Petrov-Garlerkin法中,采用径向基函数耦合多项式基函数来构造形函数,通过提高多项式基函数的阶数,可以很容易构造任意阶次的形函数,因此能有效的避免剪切自锁现象的发生.

为检验高次多项式基函数能够有效的避免剪切自锁现象,在此考虑对边固支另对边简支中厚方板,取边长为a=1 m,弹性模量E=200 GPa,泊松比μ=0.3,受均布面载荷ε0=1MPa.利用MQ径向基函数附加二次多项式进行插值近似计算.板上布置225(15×15)个规则离散节点,具体计算方法和步骤参考文献[6,7].假设板厚跨比为0.001,其中点挠度的级数解[8]为wmax=0.00192q0a4/Q.三个位移变量w、θx和θy使用相同的插值函数进行插值,插值函数使用不同阶次的多项式基函数进行构造.图2给出了沿x轴方向(两固支边中点连线上)在不同阶数多项式基函数的情况下挠度的变化曲线.从图中可以看出使用一阶多项式基函数时(m=3),即线性多项式时,发生明显的剪切自锁现象.当使用二次多项式基函数时(m=6),基本上消除了剪切自锁现象.但是,当多项式基函数的项数取值继续增大时,则需要更多的节点来插值位移变量,因此影响域的大小要明显增大,这样会增大计算量.

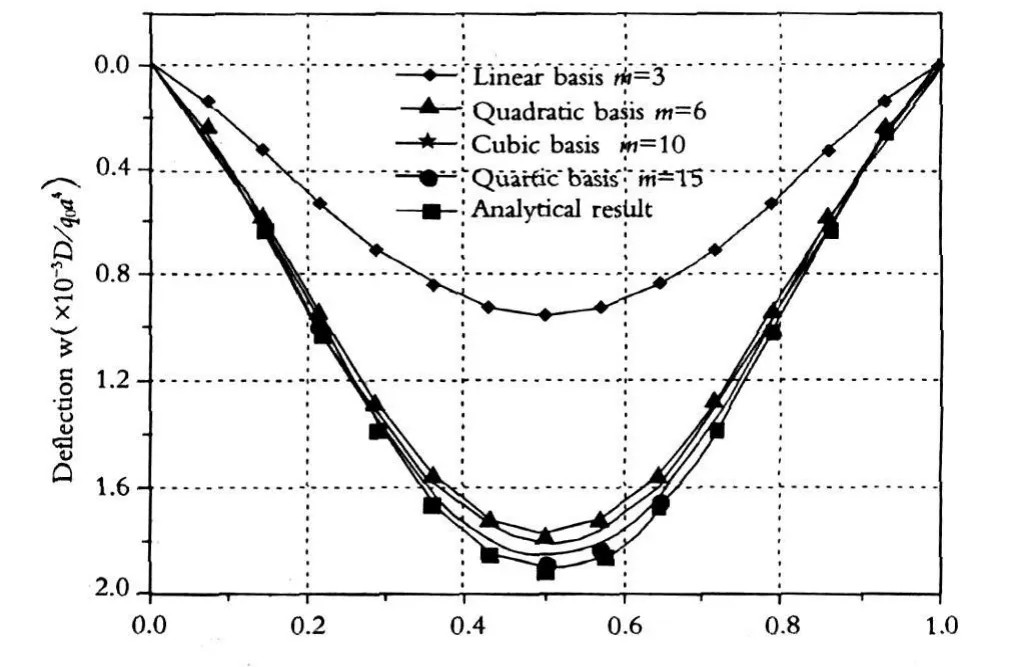
图2 不同阶数多项式基函数下挠度的变化曲线

3.2 位移变量分别插值

另一种避免剪切自锁现象的有效方法是对三个位移变量采用不同阶次的形函数进行插值,即转角采用比挠度低一阶的插值函数.由于w的连续性要求比θx和θy高一个阶次,因此可以采用如下插值方式

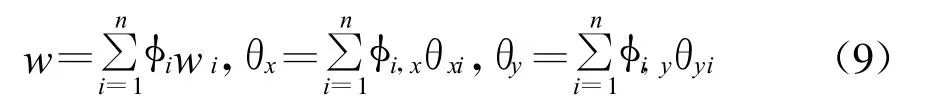
该方法能够有效地消除剪切自锁现象的发生.对于上面的算例,表1列出了在不同阶数多项式基函数和不同厚跨比时,位于板中点的最大挠度值.

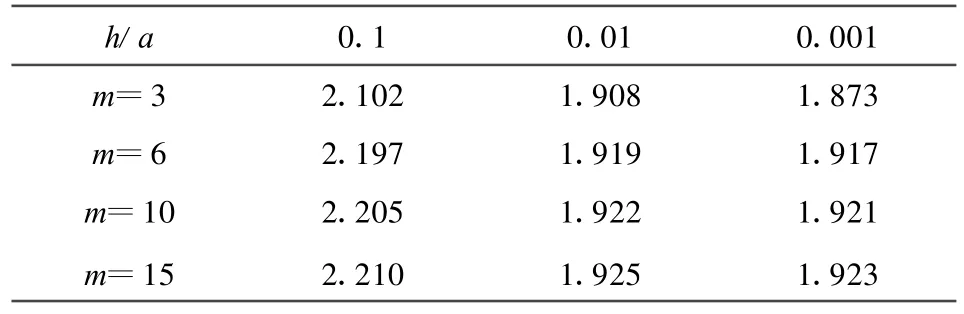
表1 分别插值时板中点的最大挠度值w(×10-3D/q0a4)

从表1中可以看出对挠度变量和两个转角变量采用不同阶次的形函数进行分别插值时,即使使用线性多项式基函数(m=3)也能够有效的避免剪切自锁现象的发生.

剪切自锁现象能得到有效地避免,就能提高求解板壳问题的效率并增强求解方法的通用性.

4 结 论

用无网格局部Petrov-Garlerkin法分析中厚板弯曲时的剪切自锁问题可以得到如下结论:

(1)在板的厚跨比大于0.01的情况下,即使使用线性多项式基函数(m=3)也不会出现剪切自锁现象.但通常选择二阶多项式基函数(m=6)可以获得更加精确的结果.

(2)使用高阶多项式基函数,如二阶多项式基函数(m=6)或二阶以上的多项式基函数时,即使板的厚跨比变得很小,也可以基本上消除剪切自锁.

(3)如果挠度和转角分别使用不同阶次的形函数进行插值,即转角采用比挠度低一阶的插值函数,则完全能够避免剪切自锁现象的发生.

[1]曹国金,姜泓道.无单元法研究和应用现状及动态[J].力学进展,2002,32(4):526-534.

[2]张 雄,宋康祖,陆明万.无网格法研究进展及其应用[J].计算力学学报,2003,20(6):730-742.

[3]Lu Y Y.,Belytschko T,Gu L.A New Implementation of the Element-free Galerkin Method[J].Comput.Methods in Appl.Mech.and Engrg.,1994,113:397-414.

[4]龙述尧.弹性力学问题的局部Petrov-Galerkin方法[J].力学学报,2001,33(4):508-518.

[5]王勖成,邵 敏.有限单元法基本原理和数值方法(第2版)[M].清华大学出版社,1997.

[6]夏 平,龙述尧,崔洪雪.用无网格局部径向点插值法分析中厚板的弯曲问题[J].应用力学学报,2009,26(2):383-388.

[7]Xia P,Long SY,Cui HX,et al.The Static and Free Vibration Analysis for the Nonhomogeneous Moderately Thick Plate by the Meshless Local Radial Point Interpolation Method[J],Engineering Analysis with Boundary Elements,2009,33(6):770-777.

[8]S.铁摩辛柯,S.沃诺斯基.板壳理论[M].北京:科学出版社,1977.

Shear Locking Analysis of Plate Bending Problem by Using Meshless Local Petrov-Galerkin Method

XIA Ping1,HU Wei-jun2,CHENG Yu-lan1
(1.College of Mechanical Engineering,Hunan Institute of Engineering,Xiangtan 411101,China;2.Department of Mechanical and Energy Engineering,Shaoyang Institute,Shaoyang 422000,China)

The shape function of the meshless local Petrov-Galerkin method is constructed by using the radial basis functions and possesses Kronecker Delta function properties.Therefore,the essential boundary conditions can be easily imposed.Causation of shear locking occurring in plate bending is analyzed.Bending problems for plate with two sides simply supported,the other two sides clamped boundary conditions,are analyzed by the meshless local Petrov-Galerkin method in this paper.It is found that the shear locking is easier to avoid in the meshless method than in the finite element method,and the measures of avoiding the shear locking are presented.

meshless local Petrov-Galerkin method;radial basis function;bending problem;shear locking

TU457

A

1671-119X(2011)01-0025-03

2010-09-07

湖南省自然科学基金资助项目(10JJ3036);湖南省教育厅科研资助项目(09C880)

夏 平(1968-),男,工学博士,副教授,研究方向:计算固体力学及其应用.