基于拟蒙特卡洛方法的动态测量不确定度评定

汉泽西，邢靖虹(西安石油大学 电子工程学院，陕西 西安710065 )

0 引言

不确定度是对测量精度的定量表征[1]。当测量系统的特性随时间发生变化时，测量系统不确定度将伴随着工作时间的延续而发生变化与漂移。目前，国内外对不确定度的表征与评定均依据1993年ISO公布的《测量不确定度指南》（简称GUM）。而我国也为了便于国际交流，于1999年发布了JJF059-1999《测量不确定度评定与表示》[2]。但二者均回避了关于动态不确定度的问题。随着动态测量在整个测试领域里的比重日益增加，动态测量不确定度的评定与应用问题已成为现代不确定度理论的核心，关于动态不确定度的问题有待深入研究。

本文提出的动态测量不确定度评定方法，注重改进了随机数的产生方法，在随机过程理论以及应用蒙特卡洛方法评定测量不确定度的基础之上，采用拟蒙特卡洛方法根据动态测量数据的特征，得到随机变量的概率分布，产生空间分布更加均匀的拟随机数，得到符合该随机变量概率分布特性的随机数值序列，作为动态测量系统的输入进行仿真，并结合GUM阐述的不确定度评定方法，完成了动态测量的不确定度评定。该方法具备较高的计算精度，稳定性和效率。

1 蒙特卡洛方法与拟蒙特卡洛方法

1.1 蒙特卡洛方法

蒙特卡洛（Monte Carlo，简称MC）方法，是一种统计试验方法，它是采用基于“随机数”的计算机随机模拟方法。其基本思想是：当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。但是，其生成算法具有确定性，这样生成的序列在本质上不是随机的，通常称之为伪随机数。

伪随机数的产生原理如下：首先基于一定方法，如线性同余法、乘同余法、逆同余法等，产生的服从均匀分布的随机数，再根据相应的数学变换得到其他分布的随机数。上述各方法均存在一定的不足，如高维不均匀性和长周期相关性现象，会导致仿真收敛速度慢及结果波动大等一系列问题。引起上述问题的一个主要原因是蒙特卡洛方法使用的伪随机数随机性过强而均匀性不足。利用蒙特卡洛方法解题主要步骤如图1所示。

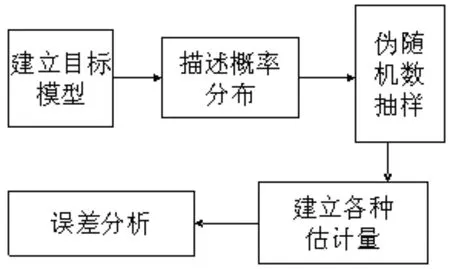
图1 蒙特卡洛方法解题步骤

1.2 拟蒙特卡洛方法

传统蒙特卡洛方法采样往往会形成“空隙和簇”的现象，造成对采样空间的搜索不充分。为了获得分布更加均匀的采样序列，人们提出了多种形式的确定性采样方法，通常称之为拟蒙特卡洛（Quasi-Monte-Carlo，简称QMC）方法。

拟蒙特卡洛方法是用精选的确定性的样本点来代替蒙特卡洛采样中的随机性样本点，其中确定性的样本点是由比伪随机数更加均匀地充满采样空间的低偏差序列通过某种变换而得的。拟蒙特卡洛方法计算的准确性及收敛速度主要取决于偏差。偏差用来度量点列在函数域上的均匀分布程度，点列分布越均匀，偏差就越小，收敛速度就加快，波动也就相应地减小，计算精度也随之提高[3]。这里用Koksma-Hlawka不等式[4-5]给出拟蒙特卡洛方法的计算误差：

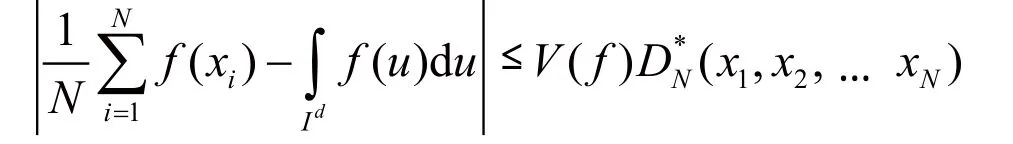
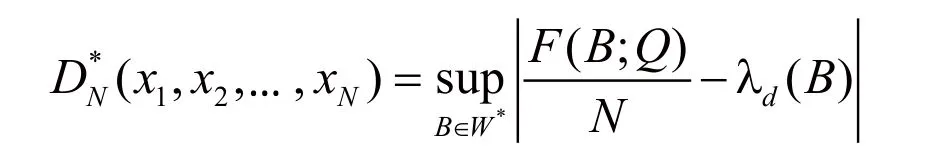
式中：Q是空间 Id中包含的点集 x1, x2,… ,xN；对于任意属于空间 Id的子集B， W*是Id上具有形式的所有子区间的集合；是d维勒贝格测度。

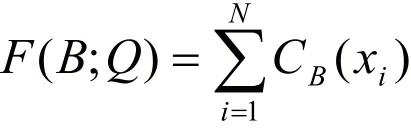
式中：CB是B的特征函数，F(B;Q)是计算满足xi∈B(1≤i≤N)的那些点的个数的函数。

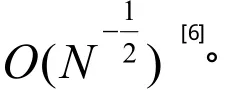
2 基于拟蒙特卡洛方法的动态测量不确定度评定

2.1 动态测量不确定度原理

为了解决传统误差评定方法的不足，人们引入不确定度的概念。结合1993年《测量不确定度指南》（GUM），将动态测量不确定度定义为：表征在相同的测量条件下（相对零时刻）合理地赋予被测量值的分散性，与测量结果相联系的参数。动态测量不确定度是对测量结果的质量的动态评价，具有时变性、随机性、关联性、动态性等特点。当实际测量系统的特性随时间发生变化时，不但会使测量结果的估计值与被测量真值的差异逐渐增大，而且一系列随机因素和未知因素对系统测量不确定性的影响增强，使测量标准差随时间发生变化，即s=s(t)，则由测量标准差所决定的测量不确定度的量值随时间延续不断增大。从而，总不确定度也是一个随时间变化的量，即测量不确定度 U= U(t)。图2所示为被测量的估计值漂移及测量不确定度随时间的变化趋势[7]。

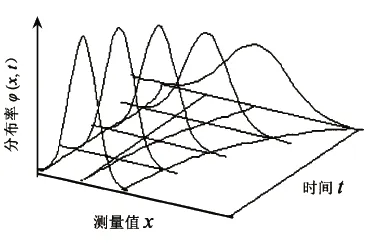
图2 测量结果漂移和测量标准差变化图

动态测量不确定度的评定通过不断引入新数据，除去旧数据，跟踪测量不确定度的变化规律，从而实现动态测量不确定度分析。

2.2 低偏差点集

低偏差点集的生成致力于点集的均匀性，伪随机数序列侧重于点集的随机性。目前统计学家已经提出了各种不同的低偏差点集，虽然构造点集的方法有差异，但这些点集序列都比伪随机数序列在单位超立方体中分布更均匀。本文采用基于Halton序列的拟随机数产生算法[8-9]：

若q为一质数，则任意自然数k均有唯一的q进制表示：

对于 有 ai∈ {0 ,1,…, q −1}，并且qr≤≤k≤≤qr+1。对任何可用下式表示的整数，且k≥1，令：

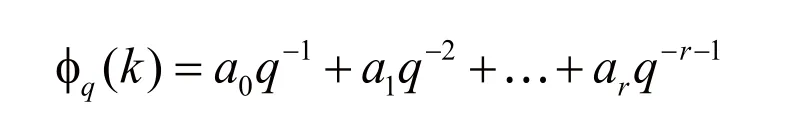
则q( k ) ∈ [ 0 , 1 ] 称为k关于基q的根式逆运算。

令pi(1≤i≤m)为m个互不相同的质数，则点集：

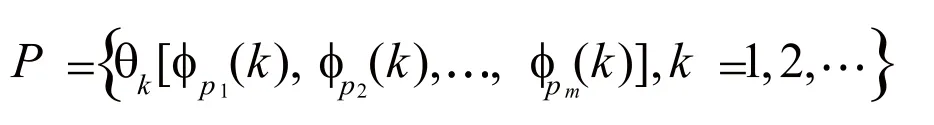
称为Halton序列。

图3和图4分别表示伪随机数序列与Halton序列抽样点同为200时在单位面积上的分布。

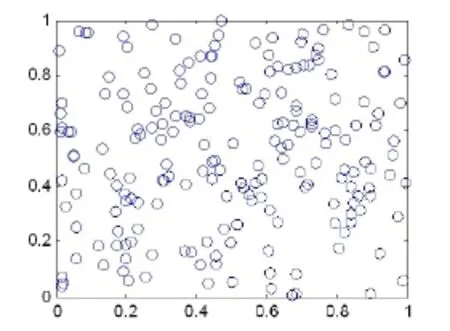
图3 单位面积上的伪随机数序列

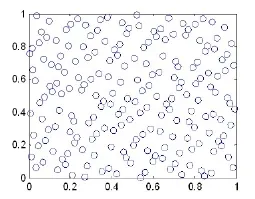
图4 单位面积上的Halton序列

由图3和图4可以看出，Halton序列抽样点的分布更加均匀，伪随机数序列分布明显有密集区和大的空白区，因此要填满整个空间就需要抽取大量的样本点，降低了计算效率。而低偏差序列在概率空间上分布较为规整，这使得拟蒙特卡洛方法比蒙特卡洛方法收敛速度更快且稳定性更高。

2.3 评定步骤

本文提出的基于拟蒙特卡洛方法的动态测量不确定度评定步骤如下：

（1）建立动态测量过程的模型方程 ；

（2）确定m时刻动态测量序列不确定度分量的概率密度函数 ；

（3）对各分量概率分布进行抽样，确定抽样样本容量M。产生满足指定概率密度函数 的拟随机数；

（5）求得m时刻标准不确定度

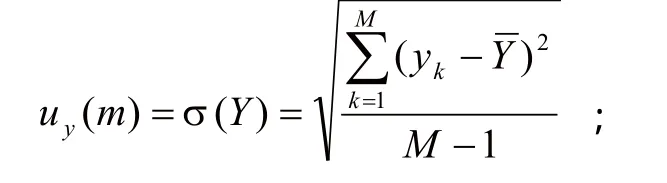
重复执行（2）～（5）步，得到系统动态测量不确定度。

由上述步骤可见，动态不确定度评定的QMC方法和MC法的根本区别就在于第（3）步中以各种不同低偏差点集取代伪随机数序列，这样不但继承了MC方法程序容易实现的优点，而且以其高精度和确定性的特点改进了传统方法的缺陷，节省了大量计算成本。

3 应用实例分析

用相同测量条件下，30次惯性陀螺的1s采样原始输出脉冲数测量值为例，计算测量数据的动态不确定度，将蒙特卡洛方法与拟蒙特卡洛方法进行了分析对比。本次实验暂不考虑环境、噪声及系统内部因素等对测量结果产生的影响，旨在突出随机数产生方法改变后，拟蒙特卡洛方法与蒙特卡洛方法用于动态测量不确定度评定的不同效果。原始测量数据见表1。

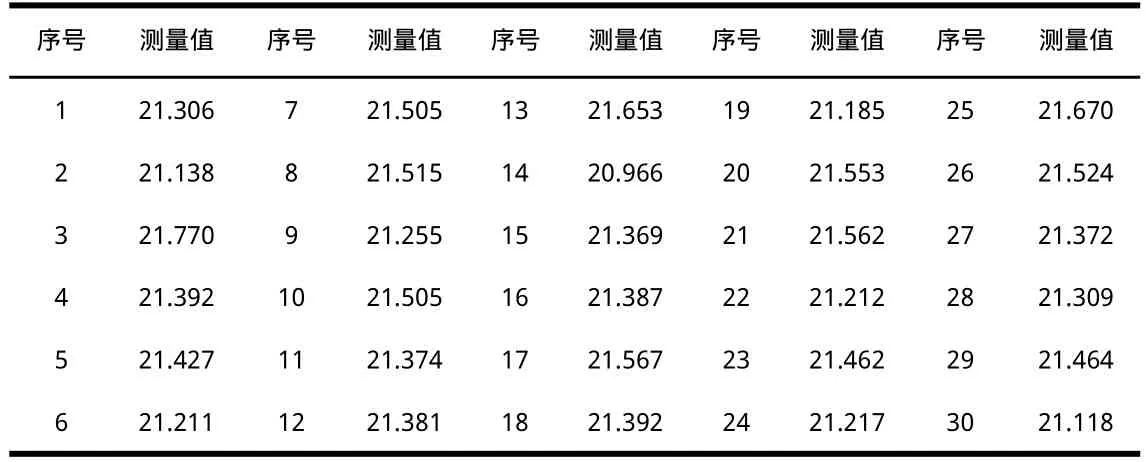
表1 惯性陀螺的1s采样原始脉冲测量数据（单位：脉冲/秒）

现取动态测量序列长度为20，即第一次计算取表1中序号为1~20的数据，第二次取表1中序号为2~21的数据，以此类推。表2为任意选取一组动态测量序列，进行不同样本容量下的仿真计算结果和相应不确定度。表3给出传统蒙特卡洛方法和本文方法计算得到的测量结果及相应不确定度。

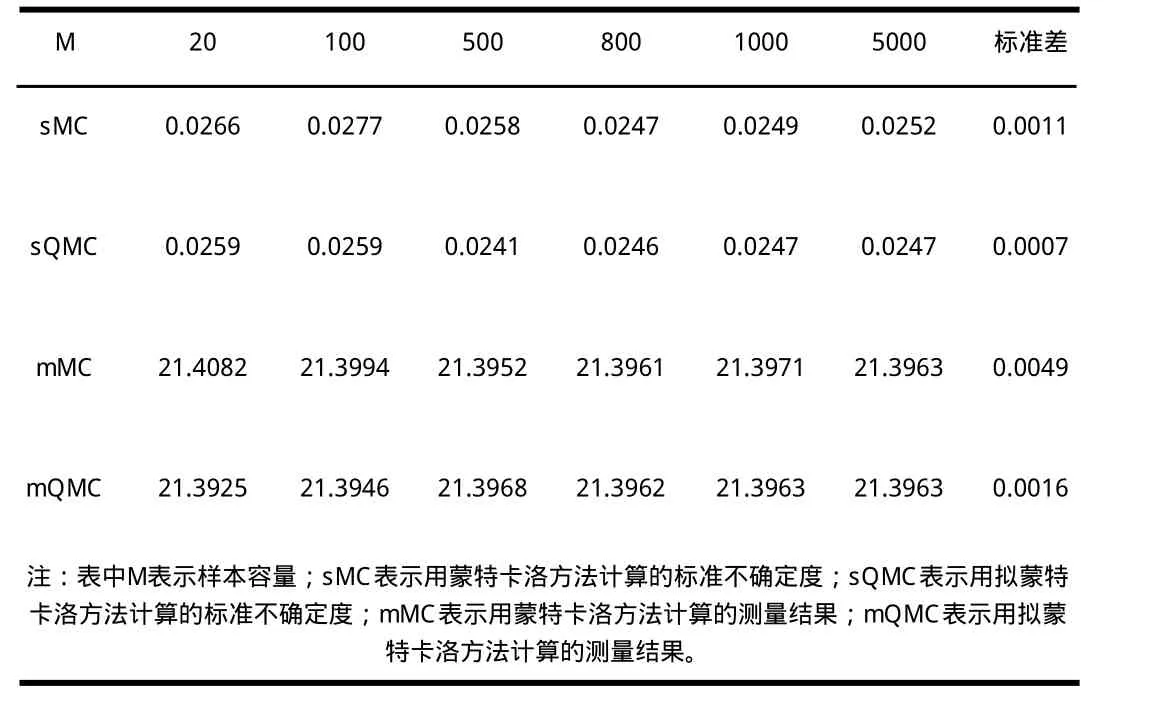
表2 不同样本容量的仿真结果

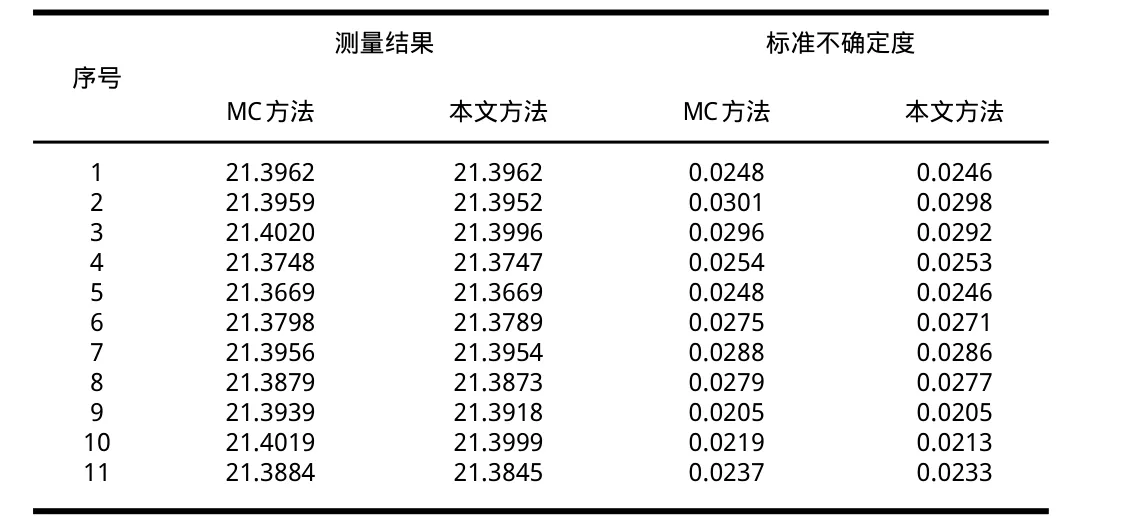
表3 不同方法得到的测量结果及标准不确定度

由表2中的数据可分析得出，当在不同样本容量情况下进行仿真时，蒙特卡洛方法收敛速度比拟蒙特卡洛方法慢，且计算结果也不如拟蒙特卡洛方法稳定。从表3中数据可以看出，本文方法评定的动态测量不确定度的精度优于蒙特卡洛方法。

4 结束语

将数论网格中的低偏差点集引入到动态不确定度分析领域，结合测量不确定度评定指南《GUM》形成了动态测量不确定度评定的拟蒙特卡洛方法，并以惯性陀螺原始脉冲数为例，进行了数值算例分析。实验结果表明，该方法的计算精度和效率优于传统的基于蒙特卡洛方法的不确定度评定方法，而且能够提供确定的误差估计，从而有效改善蒙特卡洛方法的缺陷。对于复杂动态系统的动态不确定度评定，拟蒙特卡洛方法能够减少大量的有限元分析次数，从而大幅度提高计算效率，可得到优于伪随机数更好的结果，收敛速度快，结果稳定，适用性强，为动态系统的不确定度评定提供了一条新思路。

[1] 高玉英,陈晓怀.应用蒙特卡罗方法计算动态测量的不确定度[J].黑龙江科技学院学报,2006,16(6).

[2] 汉泽西,肖志红,董浩.现代测试技术[M].北京:机械工业出版社,2006:169-171.

[3] 戴鸿哲,王伟.结构可靠性分析的拟蒙特卡罗方法[J].航空学报,2009,30(4):2-5.

[4] 张艳林,朱丽莎,张义民,等.机械强度可靠性灵敏度分析的拟蒙特卡罗法[J].东北大学学报,2010,31(11):2-4.

[5] Ronald Kleiss,Achilleas Lazopoulos.Error in Monte Carlo,quasi-error in Quasi-Monte Carlo[J].Computer Physics Communications,2006,175:93-115.

[6] 孟轲.拟蒙特卡罗方法在Variance-Gamma模型里的应用[D].北京:清华大学,2009:11-12.

[7] 谢少锋,陈晓怀,张勇斌.测量系统不确定度分析及其动态性研究[J].计量学报,2002,23(3):1-2.

[8] B IPM/JCGM.Evaluation of measurement data-supp lement 1 to the‘guide to the expression of uncertainty in measurement’- propagation of distributions using a monte carlo method[J].D raft Supp lement 1,2006:4-12.

[9] Xavier Legrand.A Quasi-Monte Carlo Integration Method Applied to the Computation of the Pollaczek Integral[J].IEEE Transactions On Power Delivery,2008,23(3):3-8.