胎儿瞬时心率信号的非线性分析

王立媛，杨立平，魏凤云

(1.哈尔滨工程大学 理学院，哈尔滨 150001；2.哈尔滨工程大学 能源与动力工程学院，哈尔滨 150001；3.长春师范学院 历史学院，长春 130032)

胎儿心脏受到血液运行状态变化和激素的影响，受脑中枢神经系统的支配[1]。胎儿的健康状况和储备能力都可以由胎儿心率的变化反映出来。故监测胎儿心率并分析其心率变异是诊治胎儿状况的一种基本方法[2]。目前，临床上普遍采用超生多普勒的方法来对处在围产期的胎儿进行监护，即在母体腹部放置超声探头来获得胎儿心跳信号。尽管获得的胎儿信号中含有母体信号和其它的噪声信号，然而通过自相关处理技术能够获得精确的胎儿心率信号[3]。以往，人们主要利用线性方法来分析胎儿心率变异性，分析结果并不令人满意。近年来，许多心脏系统生理学研究指出心率数值序列包含着不规则性，具有典型的非线性行为。胎儿心率变异性和貌似不规则性被解释成混沌动力学的复杂时间演化特征[4]，而混沌是指发生在确定性系统中的貌似随机的不规则运动，是一种始终限于有限区域、轨道永不重复、形态复杂的运动，具有对初值极端敏感性、分数维等特点。生理系统出现了混沌已经得到证明，一个正常的成年人的心脏波动是混沌的，当混沌特征减少时人开始生病，混沌消失时系统就稳定了，这时人也就死亡了[5]，并且推断变异性减少、周期增强意味着系统的疾病和老化。

因此，本文选择了非线性方法来分析健康FHR时间序列，这能够了解FHR变异性的动力学特性，给出关于健康胎儿状况的非线性评价指标。

1 研究内容

以年龄为25～32周岁、妊娠周期在37～41周的孕妇为研究对象，利用一台超声多普勒监护仪测得胎儿心率信号。首先，由超声传感器发出超声脉冲，再将通过母体腹部反射的脉冲回声通过高频放大器放大，最后通过带通滤波解调就可得到胎儿的心跳信号。胎儿瞬时心率是由公式 60/T计算得到，心率单位是每分钟心脏搏动的次数，通常表示成bpm，T是通过自相关技术找到解调的两个相邻心跳信号的时间间隔。监护仪利用串口与计算机相连接，将采集的FHR信号传输并存储到计算机中。计算机采样频率是2Hz，这85例健康信号的采集时间是20～40min，相应的数据点是从2353～6898。

本文从监测的信号中选择了85例健康信号进行非线性分析，而健康的胎儿是指排出下列情况：a.多胎；b.孕妇有高血压，心脏病和甲状腺；c.孕妇吸毒，酗酒；d.死胎或缺氧；e.宫内生长受限。

2 研究方法

非线性方法是描述生理系统动力学特性的一种有效途径，该方法可以用于研究各种心率变异性。通过对胎儿心率信号进行相空间重构[6]，混沌判定特征量关联维和最大 Lyapunov指数的计算以及替代数据分析的方法对胎儿心率信号所表征的系统动力学行为进行分析。

2.1 吸引子的重构

分析一个系统动力学特性的第一步是进行相空间重构，本文利用时间延迟法对吸引子进行重构，其原理是通过合理选择延迟量 和嵌入维数 m，对一维时间序列进行重构，得到系统在相空间的吸引子，文中用x(i)代表所采集到的FHR信号数值：

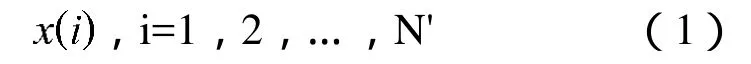
产生一组m维向量：

2.2 最大Lyapunov指数(LLE)

一个混沌系统具有整体稳定性和内在不稳定性。内在不稳定性导致系统对初始条件极其敏感。刻画混沌系统的内在不稳定性的一种方法是计算LLE，LLE能够充分的刻画混沌系统的特征，应用最为广泛。对LLE的计算基于Rosenstein[7]等提出的算法。在重构吸引子后，算法在轨道上搜索每个相点的最临近点，并假设第j对最临近点按照最大LLE的速度分离：

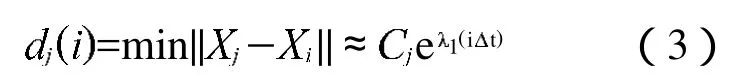
在式(3)两边取对数可以得到

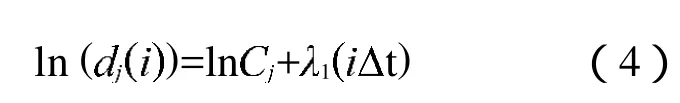
方程(4)是一系列近似平行的直线(j=1，2，…，N)，每个直线的斜率近似的与成比例。最大LLE使用最小二乘拟合平均直线的方法来定义

2.3 关联维

胎儿心脏是一个非常复杂的动力学系统，关联维是描述相空间中状态矢量分布的复杂性指标。利用文献[8]提出的算法来计算 FHR信号的关联维，首先利用坐标延迟法将实测的 FHR时间序列重构到一个维的相空间中，然后计算：

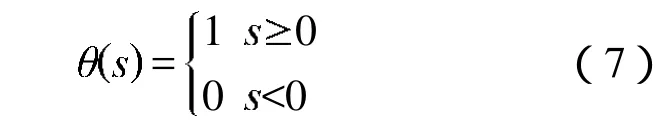
3 结果分析

3.1 吸引子重构图

图1是一例妊娠周期为39周的健康胎儿的FHR时间序列图，图中显示胎儿瞬时心率信号呈现一定的周期性，又类似噪声的背景；图2是由三维相空间重构得到的吸引子，由图可见，这是一个集中在有限区域、不断扭曲、缠绕的非常复杂的吸引子。

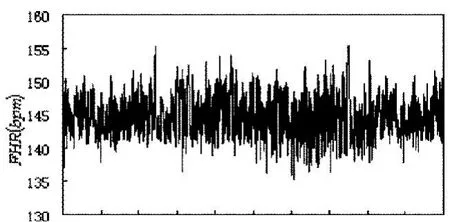
图1 FHR信号时间序列Fig.1 Time series of FHR signal

图2 FHR信号嵌入到三维相空间的重构吸引子Fig.2 Reconstructed attractor of FHR in 3-dimensional phase space

3.2 关联维计算结果

以一例妊娠周期为39周的健康胎儿为例，计算得出健康的FHR信号在嵌入维m从1至30情况下ln 随ln变化关系，如图3所示，图中两条虚线之间部分是一段很好的线性区域，对于每个嵌入维m这段线性区域的斜率就是对应的关联维2(m)；关联维2随着嵌入维m的变化关系如图4所示，由图中可以看出，随着嵌入维 的增加关联维2也在增加，当 m为19时关联维2达到了饱和，这个饱和值5.83就是这例健康FHR信号的关联维。采用同样的方法对85例健康的FHR信号进行了关联维2计算，结果为5.68±0.34(平均值±标准偏差)。

3.3 最大Lyapunov指数计算结果

以一例妊娠周期为39周的健康胎儿为例，计算出这例健康胎儿的最大 Lyapunov值，图5是拉伸因子的对数随迭代步数的变化关系，由图可见，图中有两条虚线，随着嵌入维的增加曲线在线性部分的斜率趋于恒定。通过计算每条曲线在虚线之间线性部分的斜率得到不同嵌入维时的最大Lyapunov指数，最终得到最大Lyapunov指数值是0.987。依据同样方法对85条健康的FHR信号进行了最大Lyapunov指数计算，得到Lyapunov指数值为0.11±0.04(平均值±标准偏差)。

图3 健康的FHR信号随ln变化关系Fig.3 Plot ofversus ln for health FHR signal

图4 健康FHR信号关联维2随嵌入维 变化关系Fig.4 Plot of2versus or health FHR signal

图5 拉伸因子的对数随迭代步数的变化Fig.5 Logarithm of the stretching factor versus number of iteration

3.4 非线性特征验证

在对时间序列分析(尤其是混沌特性分析)中，通常是通过直接计算 Lyapunov指数和关联维数等特征量来研究，但这要求所研究的时间序列的数据量N很大(即希望N→∞)，而对短数据量的时间序列往往会出现一些虚假结果，而替代数据测试能够克服由于噪声和短期数据这些因素给计算结果带来的不利影响，所以进行了替代数据测试。文中通过振幅调节傅里叶变换法(AAFT方法)产生替代数据，对85例健康FHR信号中的每一例原数据都相应产生了19组替代数据，对每一条原数据与其产生的替代数据集进行了关联维和LLE的计算，图6和图7是以一例妊娠周期为39周的健康胎儿为例计算得出的替代数据集和原数据的关联维和LLE，图中显示替代数据集与原数据有明显差别，说明这例 FHR信号具有非线性特征，依照同样的方法对85例健康的FHR信号进行了替代数据分析，计算结果表明85例FHR信号与其产生的替代数据集都有显著差别，拒绝虚假设，说明 FHR信号以95%的置信度被认为具有非线性特征。

图6 原数据及替代数据的2随重构维m的变化Fig.6 Plot of 2versus m for original data and surrogate data

图7 原数据与替代数据的LLE随m的变化Fig.7 Plot of LLE versus m for original data and surrogate data

4 讨论

本文利用非线性分析方法对妊娠周期为37～41周的85例健康的FHR信号进行分析，分析结果表明：

(1)健康的FHR信号重构的三维相图中运动轨线被吸引到一个有限区域内，这是一个不同于周期和噪声的非常复杂的奇怪吸引子。

(2)健康 FHR信号的关联维是分数维，为5.68±0.34，最大Lyapunov指数大于0，为0.11±0.04，说明信号具有对初始条件的敏感依赖性，这说明健康胎儿FHR信号描述的是一个高维混沌系统。

(3)以关联维和最大Lyapunov指数为统计量进行替代数据测试，结果表明 FHR信号与替代数据集有显著区别，说明 FHR信号以95%的置信度被认为具有非线性特征。

[1]Kamath M V，Fallen E L.Power spectral analysis of heart rate variability：a noninvasive signature ofcardiac autonomic function[J].Crit Rev Biomed Eng，1993，21(3)：245-311.

[2]Ilse J M，Eduard J H，David J.Fetal heart rate in relation to its variation in normal and growth retarded fetuses[J].Euro Obs，2000，89(1)：27-33.

[3]Xiao H，Luo K Q，Zhang Z X.A new algorithm for detecting fetal heart rate using ultrasound Doppler signals[J].Ultrasonic，2005，43(6)：399-403.

[4]Papadimitriou S，Bezerianos A.Nonlinear analysis of the performance and reliability of wavelet singularity detection based denoising for Doppler ultrasound fetal heartrate signals[J].Int J Med Inform，1999，53：43-60.

[5]Goldberger A L，West B J.Chaos and fractals in human physiology[J].Sci Am，1990，262：43-49.

[6]Takens F.Detecting strange attractors in fluid turbulence[M].Berlin：Springer，1981：366-381.

[7]Rosenstein M T，Collins J J，Luca C J.Visualizing the effects of filtering chaotic signals[J].Comput，Graphics 1994(18)：587-592.

[8]Harikrishnan K P，Ambika R G，Kembhavi A K.A non subjective approach to the GP algorithm for analyzing noisy time series[J].Physica D，2006，215：137-145.