基于GA-ANFIS的边坡稳定性评价
2011-03-15林咸志
林咸志,薛 涛,余 鹏,陈 青
(1.浙江华光潭水力发电公司,浙江 临安 311322;2.河海大学土木工程学院,南京 210098)
基于GA-ANFIS的边坡稳定性评价
林咸志1,薛 涛2,余 鹏2,陈 青2
(1.浙江华光潭水力发电公司,浙江 临安 311322;2.河海大学土木工程学院,南京 210098)
自适应神经模糊推理系统将模糊推理的可解释性和神经网络的自适应、自学习的能力结合起来,克服了边坡岩体的不确定性问题带给边坡稳定性分析的巨大困难,同时针对模糊推理系统内部参数设定的合理性问题,建立了基于遗传算法的自适应模糊推理评判模型。结果表明,GA-ANFIS评判模型结果与现场监测情况吻合,从而使其成为边坡稳定性评价的一种有效方法。
GA-ANFIS模型;评价指标;不确定性;边坡稳定性评价
1 前言
边坡稳定性评价是一项较为复杂的综合性工作,其最基本的评价指标是极限平衡方程的解。传统的方法是采用以安全系数为度量指标的定值法,这种方法经过长期的实践证明是一种有效的工程实用方法,但却存在计算结果与实测结果不一致的缺陷[1]。这是因为边坡系统是一个开放复杂的系统,边坡岩体是性质极其复杂的地质介质,其力学参数、结构面分布规律、工程性质等复杂多变,具有强烈的不确定性。这些不确定性的客观存在给边坡稳定性分析带来了很大的困难。因此应用模糊数学,采用不确定的方法分析边坡稳定性已经成为许多专家学者的研究对象。如李彰明针对边坡稳定性的普遍问题,遵循重要性、独立性和易测性原则,建立了边坡稳定性分析的模糊综合评价模型,并构造了相关因素边界值矩阵[2]。汪益敏、洪海春等在考虑影响边坡稳定性因素模糊性的基础上采用多指标因素模糊综合评价方法,对边坡岩体稳定质量进行了多级模糊综合评判研究[3,4]。徐卫亚等通过对边坡稳定性分析中模糊因素的研究,提出了一种新的边坡模糊稳定性分析方法,建立了边坡稳定性分析的模糊数学模型,并给出相应的求解方法[5]。杨建贵等将模糊随机可靠度理论应用于边坡的稳定分析,建立基于几何法计算广义可靠指标的数学模型,并根据模型的特点,引入加速遗传算法寻找最小可靠指标,导出计算边坡稳定的模糊随机可靠度算法[6]。考虑到在模糊推理系统建立的过程中,其内部参数(如训练次数、聚类影响范围、接受率、拒绝率、学习方法等)取值的合理性会影响最终结果的精度,因此,采用基于遗传算法优化自适应模糊推理系统(GAANFIS)的方法对华光潭一级水电站厂房后边坡滑坡体进行了预测。通过与现场实测结果对比,结论可靠。
2 概况
2.1 工程概况
华光潭一级水电站位于浙江省临安市昌化江上游的巨溪河段,两岸及谷底基岩裸露,河流纵坡大。发电厂厂区位于河道右岸,主厂房、副厂房和升压站依次从河道的上游往下游呈“一”字形排列。厂区地坪高程230 m,厂房后山坡高程232~600 m,调压井井口高程471.98 m。工程于2002年4月开工建设,2005年6月下闸蓄水,2005年12月基本建成。
2.2 厂房后边坡工程地质特性
根据一级水电站厂房后边坡构造发育性质及发电引水隧洞揭露的地质现象,厂房区NW向小断裂发育,上坡外侧自现有上坡线向山内延伸长约80 m范围内岩石风化较强,一般呈全—强风化状。从平硐揭露情况看,深度约50 m范围内岩石中走向290°—320°的裂隙极其发育,多数充填次生粘土及碎石,一般厚0.5~2 cm,较厚者达20 cm,局部地段遇有空洞现象。马道上钻孔揭露全—强风化岩石分布厚度11~16 m,多种迹象表明,一级水电站厂房后山坡岩石的风化及破碎程度与构造及变形相关性很强。
2.3 厂房后边坡破坏特征
2008年6月,在厂房后边坡坡脚挡墙上发现5 cm左右的拉裂缝(见图1),后通过现场踏勘和调查发现:边坡中下部已发生明显的水平位移和沉降;边坡中部的截水沟浆砌块石已严重开裂、错位;中上部发育有多条被腐殖层和土壤层覆盖的、开度可达20~40 cm的拉裂面(见图2)。从钻孔岩芯可见缓倾角软弱结构面,而且缓倾角结构面上铁锰渲染严重,水迹特征明显。

图1 边坡挡墙开裂状况Fig.1 Cracking status of slope retaining wall

图2 坡面开裂状况Fig.2 Status of slope cracking
鉴于此,厂房后边坡的整体稳定问题非常突出,因此查清该边坡的变形破坏机理、合理地评价其稳定性、科学地预测其在运营期间可能发生的变化显得尤为重要。
3 GA-ANFIS模型的建立
模糊推理[7]本质上就是将一个给定输入空间通过模糊逻辑的方法映射到一个特定输出空间的计算过程,具有万能逼近性。人工神经网络[8]具有强大的自学习、自适应和非线性映射能力,模糊推理不具备自学习功能,但能很好地模拟人脑的推理功能。自适应神经模糊推理系统(adaptive neuro-fuzzy inference system,ANFIS)[9]充分利用了两者的优点,利用神经网络中一些行之有效的算法从经验数据中获取模糊规则和确定隶属函数,并可利用神经网络结构来实现模糊推理,将模糊推理的可解释性和神经网络的自适应、自学习能力进行有机结合。
应用模糊数学解决不确定的问题有其优越性,然而在模糊推理系统建立的过程中,其内部参数(如训练次数、聚类影响范围、接受率、拒绝率、学习方法等)设定的是否合理,会影响最终结果的精度。由于对神经模糊推理系统内部参数的调整是一个优化组合问题,而优化组合正是遗传算法之所长。在此,利用遗传算法优化自适应模糊推理系统的参数。
3.1 ANFIS 参数设置
ANFIS参数设置:a.将训练次数、聚类影响范围、压缩系数、接收率、拒绝率、训练算法确定为需要优化的参数;b.训练次数选定为37~100,采用6位二进制编码;c.聚类影响范围选定为0.2~0.5,采用2位二进制编码;d.压缩系数选定0.8~1.5,采用3位二进制编码;e.接收率选定0.2~0.5,采用2位二进制编码;f.拒绝率选定0.1~0.4,采用2位二进制编码;g.训练算法共两种,采用1位二进制编码。最后按以上顺序将编码进行串联组合得到16位二进制码作为一个个体。
3.2 遗传算法参数设置
设定生成10个样本(每个样本为16位二进制码)作为初始种群;训练代数为30代;代沟为0.9;变异概率为0.043;选择方式为随机遍历抽样;交叉方式为单点交叉。
3.3 适应度值函数
一般取均方根误差作为适应度值评价函数。

式(1)中,di为实测值与预测值之差;n为数据序列长度。
4 基于GA-ANFIS的边坡稳定性评价
4.1 边坡稳定性复合指标参数的确定
已有研究表明,边坡岩体稳定性是多种非线性耦合作用的结果[10,11]。其中岩石强度、岩体结构和风化情况是影响边坡稳定性的内在因素;水的作用、施工方法等则是影响边坡稳定性的触发因素。CSMR 分类体系[12]是 RMR -SMR 系统[13]的一种应用,它是在RMR-SMR体系的基础上,引入高度修正系数和结构面修正系数而提出的一种用于边坡岩体质量评价的方法,具体表达式见式(2):
CSMR= ξRMR-λ(F1×F2×F3)+F4(2)式(2)中,ξ为坡高修正系数;RMR为地质力学围岩分类;λ为结构面修正系数;F1为不利结构面与坡面倾向之间平行程度的调整因子;F2为平面破坏中结构面倾角调整因子;F3为坡角与结构面倾角之间关系的调整因子;F4为开挖方法调整因子。
由于华光潭一级水电站厂房后边坡的滑动力学特征为牵引式滑动,即由边坡下部的滑动带动上部边坡的变形破坏,所以边坡下部的稳定至关重要,故选取下级滑面作为优势不连续面进行深入研究。
已有勘查资料显示:边坡下滑面附近的岩石为强风化状态,呈碎块状;钻孔ZK201在滑面附近的RQD为0,钻孔ZK202在滑面附近的RQD为50%,钻孔ZK203在滑面附近的RQD为0% ~50%,钻孔ZK205在滑面附近的RQD为20%;滑面附近节理较发育,节理面粗糙,其内充填软性粘土及泥浆,厚度为1~5 cm;正常情况下底滑面与地下水位较接近,在持续降雨时则低于地下水位。沿滑面多为砾包泥状的破碎岩石。下级滑坡后缘高程为310 m,前缘高程为232 m,因此坡高为78 m,边坡产状为45°∠35°,滑面产状40°∠10°,边坡开挖方式为预裂爆破。
综上所述,可确定所需的5个参数值。
1)坡高修正系数ξ见式(3)。

式(3)中,Hr=80 m;H为边坡高度。因此可得ξ=1.01。
2)RMR综合了岩石强度、RQD、不连续面间距、不连续面状态、地下水状况等因素来反映岩体质量的指标。边坡岩体各影响因素相应的得分情况见表1。

表1 RMR值影响因素得分情况Table 1 Scores situation of RMR in different factors
由表1可得:RMR=4+3+15+7+4=33。
3)结构面修正系数λ。根据表2,结构面修正系数λ=1。

表2 结构面修正系数λTable 2 Correction factor λ of structural surface
4)边坡结构系数 SSC。将 F1、F2、F3整合为边坡结构系数SSC,其表达式见式(4):

式(4)中,F1为结构面倾向与坡面倾向的关系;F2为结构面倾角的影响;F3为坡角与结构面倾角的关系。根据平面滑动的标准判断,可知F1=0.85,F2=0.15,F3= -60,故 SSC= -7.65。
5)施工方法影响系数F4。根据表3,F4=10。

表3 施工方法影响系数Table 3 Influence coefficient of construction method
4.2 边坡稳定性评价的GA-ANFIS模型实现
选取国内已建水电工程边坡的22个工程实例[14]作为学习和检验样本,样本的输入参数可见表4。经过遗传算法对训练参数进行30代进化,可以得到经过优化的ANFIS内部参数(见表5)。通过对学习样本和检验样本的输出结果分析可知,GAANFIS具有较高的预测精度,学习样本的误差全部为0,而检验样本的预测误差均在10%以下,已建立起边坡影响参数与安全系数之间的模糊隶属关系,可以用来预测影响条件复杂的边坡岩土体。从预测华光潭一级水电站厂房后边坡下级滑动面安全系数的情况看,在持续降雨的情况下,边坡的安全系数为0.96,处于失稳状态。

表4 学习、检验和预测样本参数表Table 4 Parameter table of learning,testing and forecast sample

表5 优化的ANFIS内部参数表Table 5 Internal parameter table for ANFIS after optimized
4.3 对比与分析
华光潭一级水电站厂房后边坡安全监测工作始于2008年11月初。利用已有勘探钻孔,布置了渗压计、多点位移计及测斜仪观测孔。2009年1月初,又根据现场揭露的地表拉裂缝分布情况,布置了多个测缝计。为了验证上述模型的可靠性,选取2009年2月到6月期间个别测点实时监测数据进行对比。
图3为250高程上深度28.5 m水平位移观测孔面向上游临空面的变形趋势,图中线条为位移曲线。图中显示,至2009年6月25日,水平位移相对于2009年2月13日增大18.13 mm,而且主要表现为整体前移。
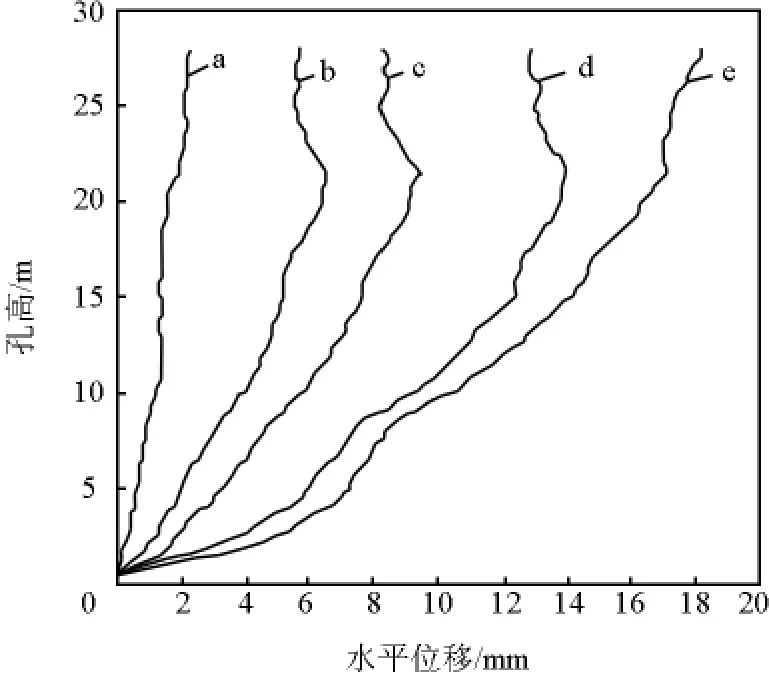
图3 水平位移随深度变化图Fig.3 Relation graph between horizontal displacement and depth
图4为310高程三向测缝计的实测结果,采样频率每月3次。图4显示,从2009年2月25日17:00至6月25日6:00,测点A的地表拉裂缝张开度增长7.8 mm,测点B所测裂缝两壁沉降差增长-17.27 mm(即拉裂缝的后壁较前壁下沉17.27 mm)。测点 C的地表拉裂缝张开度增长1.5 mm。

图4 地表拉裂缝张开度变化时程曲线Fig.4 The time history curve of joint opening degree of tension crack in the surface
图3和图4均显示,在2009年2月16日到3月10日期间,边坡变形量较大。而该段时间正是当地持续降雨过程。鉴于此,可以认为基于GAANFIS的边坡稳定性预测模型的结论可靠。适用于预测本质上复杂、多变,且具有强烈不确定性岩土体的安全状态。
5 结语
1)华光潭一级水电站厂房后边坡的变形破坏,是斜坡表部岩体蠕动—滑移—拉裂变形长期发展的结果。伴随着坡体临空面的产生,原岩产生差异卸荷回弹,导致浅表部岩体破碎,厚大的覆盖层增大了坡体的自重,坡体在自重应力场的长期作用下发生剪切蠕动,边坡的下部失稳导致了坡体中上部失去阻滑力,引起大范围的滑动变形。
2)华光潭梯级水电站为III等工程,引水发电系统和发电厂房为三级建筑物,因此一级厂房后边坡的稳定安全系数需达到 1.15 ~1.25[15]。而持续降雨条件下的预测结果却不能达到规范要求,故需治理以提高其安全系数。
3)从对比分析可以看出,华光潭一级水电站厂房后边坡稳定性预测结果与实测结果一致,说明基于模糊理论的自适应神经模糊推理系统适用于预测本质上复杂、多变,且具有强烈不确定性岩土体的安全状态。
[1]姚爱军,薛延河.复杂边坡稳定性评价方法与工程实践[M].北京:科学出版社,2008.
[2]李彰明.模糊分析在边坡稳定性评价中的应用[J].岩石力学与工程学报,1997,16(5):490 -495.
[3]汪益敏.边坡岩体稳定质量的模糊评判[J].华南理工大学学报,1997,15(4):110 -115.
[4]洪海春,徐卫亚,叶明亮.基于模糊综合评判的边坡稳定性分析[J].河海大学学报,2005,33(5):557 -562.
[5]徐卫亚,蒋中明,石安池.基于模糊集理论的边坡稳定性分析[J].岩土工程学报,2003,25(4):409 -413.
[6]杨建贵,蔡 新,张永乐.边坡稳定的模糊随机可靠性分析[J].河海大学学报,2002,30(1):58 -62.
[7]吴望名.模糊推理的原理和方法[M].贵州:贵州科技出版社,1994.
[8]Martin T Hagan,Howard B Demuth,Mark H Beale.神经网络设计[M].北京:机械工业出版社,2002.
[9]吴晓莉,林哲辉.MATLAB辅助模糊系统设计[M].西安:西安电子科技大学出版社,2002.
[10]谷德振.岩体工程地质力学基础[M].北京:科学出版社,1979.
[11]Hoek E,Bray J W.岩石边坡工程[M].北京:冶金工业出版社,1981.
[12]葛 华,吉 峰,石豫川,等.岩体质量分级方法——CSMR法的修正及其应用[J].地质灾害与环境保护,2006,17(1):90-94.
[13]Romana M.SMR classification[C]//Proceedings of the 7thInternational Congress in Rock Mechanics.Beijing:International Society for Rock Mechanics(ISRM),1992.
[14]陈昌彦,王思敬,沈小克.边坡岩体稳定性的人工神经网络预测模型[J].岩土工程学报,2001,23(2):157-161.
[15]张发明.地质工程设计[M].北京:中国水利水电出版社,2008.
Evaluation of slope stability based on GA-ANFIS
Lin Xianzhi1,Xue Tao2,Yu Peng2,Chen Qing2
(1.Zhejiang Huaguangtan Hydropower Co.,Ltd.,Lin’an,Zhejiang 311322,China;2.College of Civil Engineering,Hohai University,Nanjing 210098,China)
Adaptive neuro-fuzzy inference system combines the interpretability of fuzzy reasoning and the ability of adaptability and self-learning of neural network,overcoming the enormous difficulties for slope stability analysis caused by the uncertainty of rock slope.At the same time,for the reasonable of parameter setting in fuzzy inference system,evaluation model of adaptive neuro-fuzzy inference based on genetic algorithm is established.It was shown that the results of GA-ANFIS model are consistent with field condition,which makes it be an effective method for slope stability evaluation.
GA-ANFIS model;evaluation index;uncertainty;slope stability evaluation
TU457
A
1009-1742(2011)03-0077-05
2009-07-15
国家重点基础研究发展规划973项目(2002CB412707)
林咸志(1966—),男,浙江临海市人,高级工程师,主要从事边坡稳定性分析研究;E-mail:85359941@163.com
