含VSC-MTDC的交直流混合系统的改进潮流算法

叶 芳，卫志农，孙国强

(河海大学能源与电气学院，江苏南京 210098)

随着电网建设的发展，直流输电在电力系统的研究和电网的实际运行中扮演着越来越重要的角色[1-2].以全控型开关器件和电压源换流器(voltage souce converter，VSC)为基础的新一代高压直流(high voltage direct current，HVDC)输电，相比于基于晶闸管的直流输电，具有直接向孤立的远距离负荷供电、更经济地向负荷中心送电、运行控制方式灵活多变等优点.因此基于VSC的HVDC(VSC-HVDC)的研究成为近年的研究热点[3-6].与两端直流输电相比，多端直流(multi-terminal direct current，MTDC)输电的输电能力更强，运行方式也更灵活，是今后直流输电的一个发展方向[7-8].含VSC-MTDC的交直流混合系统的潮流计算是分析VSCMTDC的稳态特性以及研究其稳态控制运行方式的必要条件，也是分析其暂态特性和相应的控制保护技术的重要基础.因此含VSC-MTDC的交直流混合系统的潮流计算研究具有重要的理论价值和实际意义.

目前采用的交直流混合系统的潮流计算方法大部分是在交流潮流计算方法的基础上扩展形成的，主要分为统一迭代求解法(简称统一法)和交替迭代求解法(简称交替法)两类[9-13].统一法是以极坐标形式下的牛顿-拉夫逊法为基础，将交流系统中的节点电压的幅值和相位与直流系统中的直流电流、直流电压以及脉宽调制(pulse width modulation，PWM)的控制变量进行统一迭代求解.该算法收敛性好，但对原有的纯交流程序继承性差，代码编制工作量大.交替法是在迭代计算过程中通过假设条件，对交直流系统方程分别进行处理，实现了交流潮流解和直流潮流解的分开迭代，对原有纯交流程序具有较好的继承性，但正是由于迭代过程中没有考虑交流变量和直流变量之间的耦合，因此收敛性不佳，精度低.

本文首先确定VSC-MTDC的稳态模型，然后导出含VSC-MTDC的交直流混合系统潮流计算的数学模型，在此基础上针对统一法和交替法存在的不足，提出改进交替迭代求解法，最后通过算例验证所提模型和算法的有效性.

1 VSC-MTDC潮流计算的数学模型

1.1 VSC-MTDC的稳态模型

在VSC-MTDC输电系统中，各VSC之间通过直流输电网络连接，对于第 i个VSC，其单相示意图如图1所示.

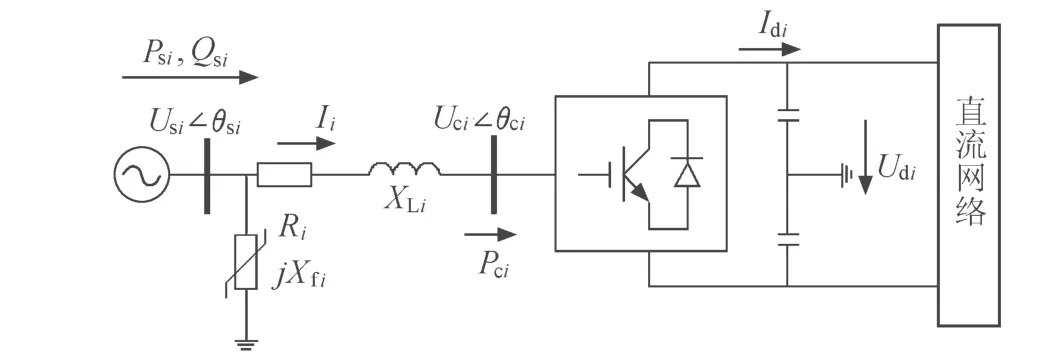
图1 单相VSC-MTDC示意图Fig.1 Schematic diagram of single-phase VSC-MTDC

假设第i个VSC输出基波电压的相量为Uci∠θci，与交流系统连接处的电压相量为Usi∠θsi，直流电压为Udi，直流电流为Idi，换流变压器阻抗为jXLi，交流滤波器阻抗为jXfi，换流器内部损耗和换流变压器损耗的等效电阻为Ri，交流系统流入换流变压器的有功功率和无功功率分别为Psi和Qsi，流入换流桥的有功功率和无功功率分别为Pci和Qci，流过换流变压器的电流为﹒Ii，假设方向如图1所示.忽略换流器的等效电阻，可得

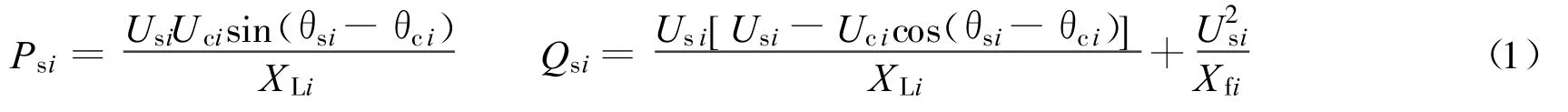
同理可推导得到

由于VSC的换流桥臂的损耗已经由Ri等效，所以直流功率Pdi应该与Pci相等，因此可得

1.2 VSC-MTDC的基本控制方式

目前，通常采用PWM技术对VSC进行控制，由式(1)可见，可以通过控制δ来间接地控制Ps，通过控制M来间接地控制Qs，从而达到对有功功率和无功功率灵活、独立控制的目的.

VSC-MTDC中，直流电压的稳定与否直接关系着系统能否正常运行以及交流侧输出电压的稳定性.如果有功发送端的VSC从该端交流系统吸收的有功功率大于接收端VSC发送到对应端交流系统的有功功率，则直流电压升高，反之降低.因此为了实现这种功率平衡，其中一端VSC必须采用定直流电压控制.另外，若直流电压恒定，则直流电流的变化量正比于有功功率的不平衡量，定直流电流控制和定有功功率控制是等效的.综合以上分析，VSC-MTDC中VSC可以选择的控制方式有以下4种:定直流电压、定无功功率控制;定直流电压、定交流电压控制;定有功功率、定无功功率控制;定有功功率、定交流电压控制.

1.3 含VSC-MTDC的交直流混合系统的潮流计算方程

按照节点是否接有换流变压器，可将节点分为直流节点和纯交流节点.设系统节点总数为n，其中VSC的个数为nc，则直流节点数为nc，纯交流节点数为na=n-nc.下面为了行文方便，假设交直流混合系统的节点编号顺序为:1～na节点为纯交流节点，其中有1个平衡节点;na+1～n节点为直流节点.

1.3.1 交流系统的潮流计算方程

对于系统中的纯交流节点(用下标a表示)，其潮流计算方程与传统的潮流计算方程相同，为

式中:U，θ——节点电压幅值和相角;G，B——节点导纳矩阵的实部和虚部;i——节点;j——与节点i直接相连的所有节点(公式中用j∈i表示)，Psai，Qsai——节点i的给定有功功率、无功功率.

而对于直流节点(用下标t表示)，其潮流计算方程为

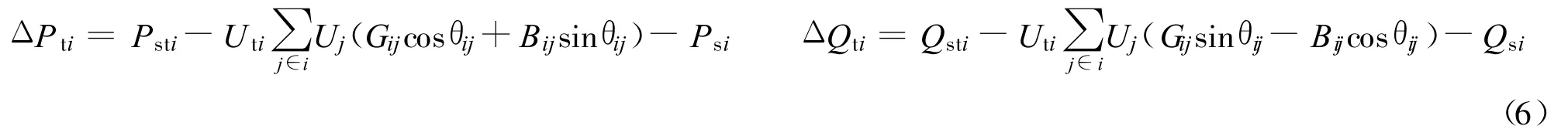
1.3.2 直流系统的潮流计算方程

根据推导建立的VSC-MTDC的稳态模型，以及直流网络方程，可得到直流系统的潮流计算方程为

式中gdij为直流网络节点电导矩阵的元素.

2 改进交替迭代求解法

对于上述建立的含VSC-MTDC的交直流混合系统的潮流计算模型，目前的算法主要有统一法和交替法2类.本文针对这2种算法存在的不足，提出了改进交替迭代求解法，具体推导过程如下:

由式(5)(6)(7)联立可得含VSC-MTDC的交直流混合系统潮流的计算方程，描述为

对式(8)进行泰勒级数展开，并忽略二阶及以上高阶项，可得牛顿-拉夫逊法的修正方程:

由此，雅可比矩阵JN的形式如下:

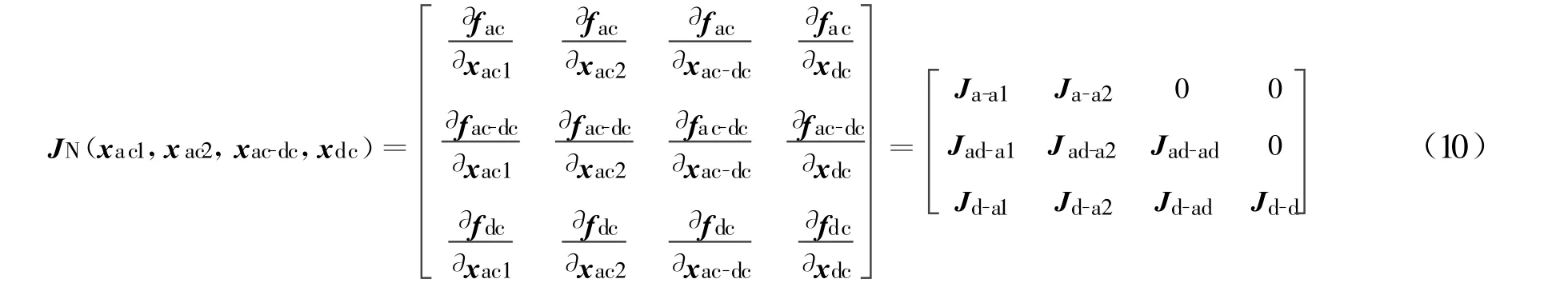
将含VSC-MTDC的交直流潮流计算方程写为

对于一个含有nc个电压源换流器的n节点系统，式(11)共有2(n-1)+4nc个方程、2(n-1)+6nc个变量，根据控制方式可以消去2nc个变量，由此可见式(11)可解.又f1为2(na-1)维矩阵，Δx1也为2(na-1)维矩阵，故J11的逆矩阵存在;f2为6nc维矩阵，Δx2为8nc维矩阵，Δx2根据控制方式可以消去2nc维，故J22的逆矩阵也存在.

将式(11)展开，即

求解式(12)得到改进交替迭代求解法(简称改进法)的形式为

从推导过程可以看出，该算法没有进行任何假设，在迭代求解的过程中完全计及了交直流系统间的相互影响，只是从数学表达形式上严格解除了交流变量和直流变量之间的耦合关系，因此，理论上它应该具有与统一法一致的精度和收敛性;同时矩阵J11，J12可以通过已有的纯交流程序计算获得，因此可以高效利用已有的纯交流系统潮流求解程序，程序编制工作量不大.

3 算例分析

为了验证本文算法的有效性，分别对IEEE-14，IEEE-30，IEEE-57节点的标准算例进行了仿真计算(电压和功率均为标幺值).图2为修改后的IEEE-14节点交直流混合系统，其中VSC1，VSC2和VSC3分别连接于节点12，13和14上，参数为:XL=0.15，R=0.006，直流电阻Rd=0.03，Xf=0.01.VSC1采用定直流电压(Ud1，ref= 2.0000)、定交流无功功率(Qs1，ref=0.2099)控制;VSC2采用定交流有功功率(Ps2，ref=-0.3601)、定交流无功功率(Qs2，ref=0.018 7)控制;VSC3采用定交流有功功率(Ps3，ref=-0.866 3)、定交流无功功率(Qs3，ref= -0.0864)控制.

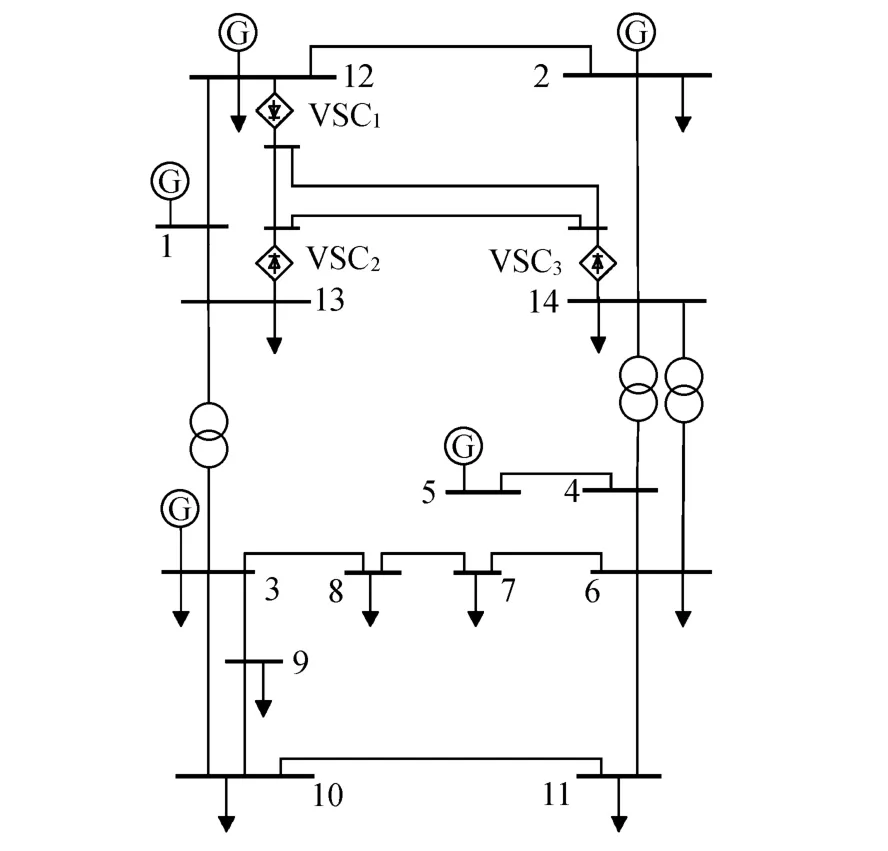
图2 修改后的IEEE-14节点交直流混合系统Fig.2 Modified IEEE-14-bus AC-DC system

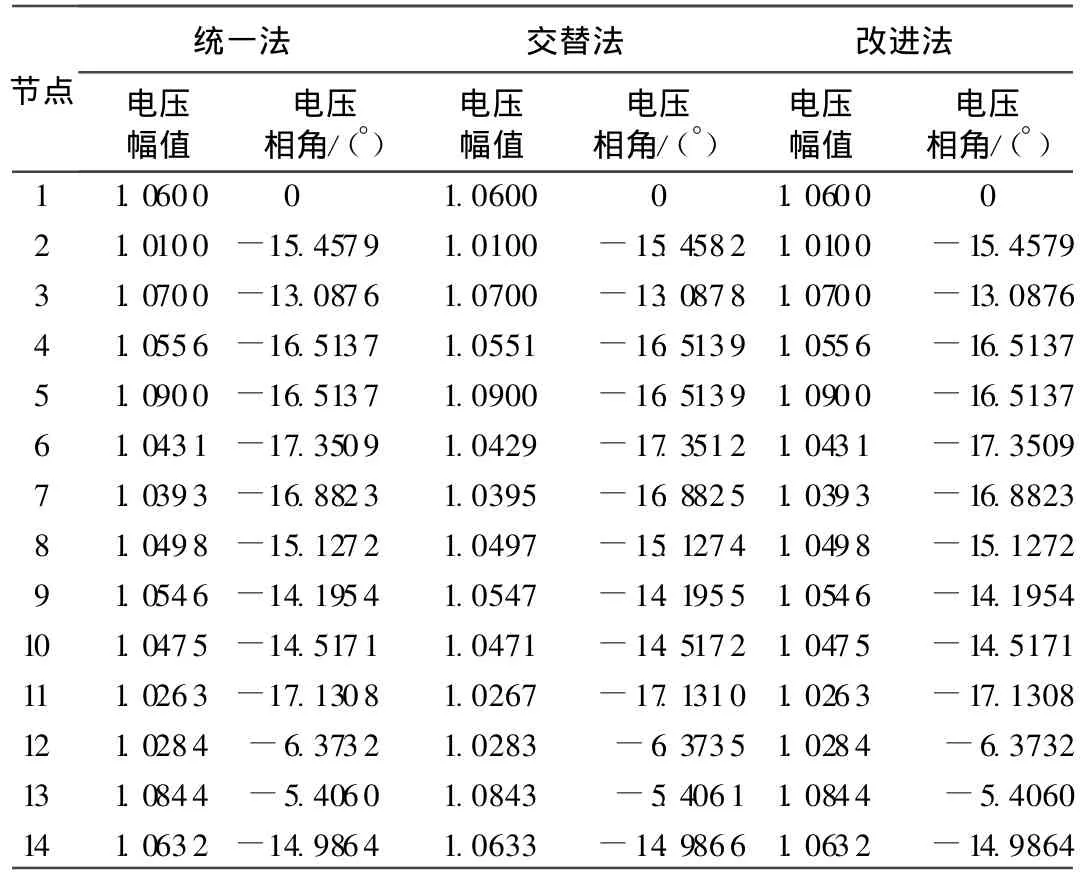
表1 交流系统潮流计算结果Table 1 Results of power flows of AC system

表1、表2分别列出了3种方法的交流系统、直流系统潮流计算结果，从中可以看出改进法与统一法的计算结果一致，这是由于改进法完全计及了交直流系统间的相互影响，从数学表达形式上严格解除了交直流变量之间的耦合关系，因此从理论上讲，它应该具有与统一法相同的计算精度.同时，由于交替法迭代过程中没有考虑交直流变量之间的耦合，导致该算法的精度不及统一法和改进法，表中结果也说明了这一点.另外，由表2可见，改进法可收敛于各VSC的控制目标.VSC1和VSC2，VSC3输出电压相角分别滞后和超前相应节点的交流母线电压相角，从而使得VSC1从交流电网吸收有功功率，VSC2，VSC3则向交流电网注入有功功率.

保持其余控制参数不变，只改变VSC2的有功功率设定值，通过改进法求得的VSC-MTDC各直流变量以及控制变量的变化曲线如图3所示.从图3可以看出，直流系统通过直流输电线路两端的电压差来传输有功功率;同时由于直流输电线路的电阻较小，在传输不同有功功率的情况下两端直流电压差均较小，有功功率的变化量主要体现在直流电流相应的增量上.另外从结果可以看出，输送有功功率的变化主要由控制量中的δ进行控制，而M基本保持不变，这个与前面得到的VSC-MTDC的运行特性相一致，也从另外一个侧面验证了改进法的有效性.

表2 直流系统潮流计算结果Table 2 Results of power flows of DC system

图3 不同Ps2，ref下VSC-MTDC各变量的变化曲线Fig.3 Curves for variables of VSC-MTDC under different P s2，ref

保持其余控制参数不变，只改变VSC2的无功功率设定值，通过改进法求得的VSC-MTDC各直流变量以及控制变量的变化曲线如图4所示.由于有功功率设定值不变，因此两端直流电压和直流电流基本保持不变，无功功率的变化主要通过调节相应交流侧节点的电压幅值得以实现，所以主要由控制量中的M进行控制，但是从表2也可以看出，由于无功功率和 δ还是存在一定的耦合作用，因此无功功率的变化也在一定程度上影响了δ.

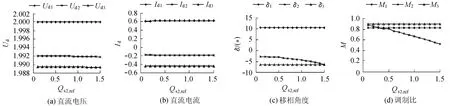
图4 不同Qs2，ref下VSC-MTDC各变量的变化曲线Fig.4 Curves for variables of VSC-MTDC under different Qs2，ref

由于VSC3有功功率和无功功率的设定值不变，所以其直流变量以及控制变量的值基本保持不变，与图3、图4结果一致.图3和图4从另一个角度说明了改进法对于不同的控制目标均有良好的收敛性.

本文还对经过修改的IEEE-30，IEEE-57节点交直流混合系统进行了潮流计算.表3给出了3个算例的3种潮流算法的计算性能比较，从计算时间上来看，改进法与其他2种算法处于同等数量级，且随着网络规模的增大，改进法依然是有效的，同时它的迭代次数没有受到明显的影响，因此改进法具有较强的实际应用价值，且程序的运行效率可满足在线实时计算的要求.

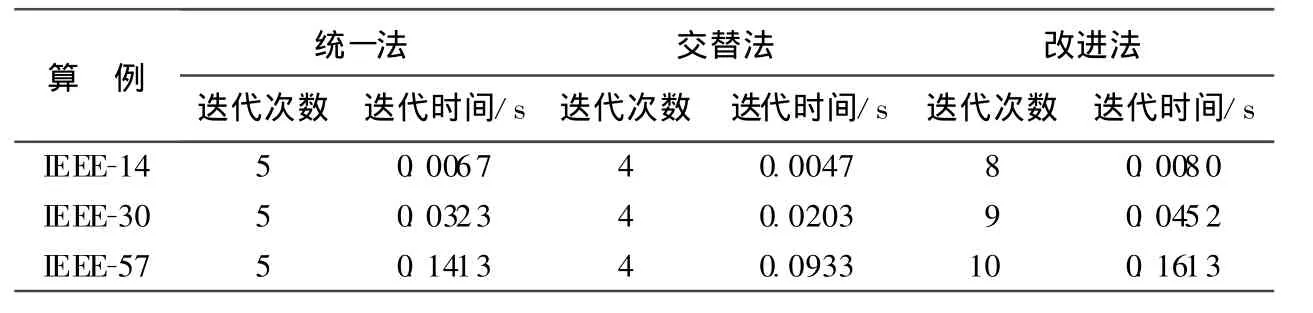
表3 3个算例下潮流算法的性能比较Table 3 Comparison of performances among three kinds of power flow algorithms

4 结 语

本文首先确定了VSC-MTDC的稳态模型，然后建立了含VSC-MTDC的交直流混合系统潮流计算的数学模型，并针对统一法和交替法存在的不足，提出了改进算法.改进算法从数学表达形式上严格解除了交流变量和直流变量之间的耦合关系，具有与统一法相当的精度和良好的收敛性.同时，改进算法可以高效利用已有的纯交流系统潮流求解程序，大大降低了程序编制难度.测试结果表明，改进算法对于不同的控制目标、不同的控制方式组合以及不同的网络规模均是正确有效的.

[1]杨勇.高压直流输电技术发展与应用前景[J].电力自动化设备，2001，21(9):58-60.(YANG Yong.High voltage DC transmission technique and its future application[J].Electric Power Automation Equipment，2001，21(9):58-60.(in Chinese))

[2]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社，2004:1-25.

[3]SCHETTLER F，HUANG H，CHRISTL N.HVDC transmission systems using voltage sourced converters design and applications[C]// IEEE PES Summer Meeting:Vol.2.Alberta，Canada:IEEE，2000:715-720.

[4]PILOTTOL A S，BIANCO A，WATANABE EH，et al.Back-to-back VSC devices:a new solution for the interconnection of asynchronous AC systems[C]//Cigre Session.Paris:[s.n.]，2000:14-203.

[5]李庚银，吕鹏飞，李广凯，等.轻型高压直流输电技术的发展与展望[J].电力系统自动化，2003，27(4):71-81.(LI Geng-yin，LV Peng-fei，LI Guang-kai，et al.Development and prospects for HVDC light[J].Automation of Electric Power Systems，2003，27(4):71 -81.(in Chinese))

[6]汤广福，贺之渊，滕乐天，等.电压源换流器高压直流输电技术最新研究进展[J].电网技术，2008，32(22):39-44.(TANG Guang-fu，HE Zhi-yuan，TENG Le-tian，et al.New progress on HVDC technology based on voltage source converter[J].Power System Technology，2008，32(22):39-44.(in Chinese))

[7]袁旭峰，程时杰.多端直流输电技术及其发展[J].继电器，2006，34(19):61-67.(YUAN Xu-feng，CHENG Shi-jie.Multi-terminal HVDC transmission technology and its development[J].Relay，2006，34(19):61-67.(in Chinese))

[8]张欢，刘天琪，李兴源，等.新型直流多端输电技术研究[J].四川电力技术，2007，30(6):1-5.(ZHANG Huan，LIU Tian-qi，LI Xing-yuan，et al.Study on novel multi-terminalDC transmission technology[J].Sichuan Electric Power Technology，2007，30(6):1-5.(in Chinese))

[9]ZHANG Xiao-ping.Multi-terminal voltage-sourced converter-basedHVDC models for power flow analysis[J].IEEETransactions on Power Systems，2004，19(4):1877-1884.

[10]LI Geng-yin，ZHOU Ming，HE Jie，et al.Power flow calculation of power systems incorporating VSC-HVDC[C].International Conference on Power System Technology:Vol.2.Singapore:IEEE，2004:1562-1566.

[11]郑超，盛灿辉.含VSC-HVDC的交直流混合系统潮流统一迭代求解算法[J].中国电力，2007，40(7):65-69.(ZHENG Chao，SHENG Can-hui.Uniform iterative power flow algorithm for systems equippedwith VSC-HVDCs[J].Electric Power，2007，40(7):65-69. (in Chinese))

[12]郑超，周孝信，李若梅，等.VSC-HVDC稳态特性与潮流算法的研究[J].中国电机工程学报，2005，25(6):1-5.(ZHENG Chao，ZHOU Xiao-xin，LI Ruo-mei，et al.Study on the steady characteristics and algorithm of power flow for VSC-HVDC[J].Proceedingsof the CSEE，2005，25(6):1-5.(in Chinese))

[13]陈谦，唐国庆，王浔.多端VSC-HVDC系统交直流潮流计算[J].电力自动化设备，2005，25(6):1-6.(CHEN Qian，TANG Guoqing，WANG Xun.AC-DC power flow algorithm for multi-terminal VSC-HVDC systems[J].Electric Power Automation Equipment，2005，25(6):1-6.(in Chinese))