基于频域滤波数字均衡器的设计

李倩然，周 南

（电子科技大学 电子工程学院，四川 成都 610054）

在音频处理中，均衡器可以改变音频信号的频响特性，从而弥补信号在传输过程中的缺陷或是达到特定的声音处理效果。通常情况下，均衡器将音频处理信号（20～20 K）按一定的规律分为10段，15段，25段或31段来进行调节。

常采用的均衡器算法是使用IIR或者FIR滤波器滤波的设计方法。这种方法有几个不足之处：IIR滤波器具有反馈回路，会出现相位偏差；FIR滤波器会造成很大的时间延迟，这对于实时滤波是非常不利的。另外，如果使用IIR或者FIR滤波器，所调节的频段越多，增加的滤波器的个数也越多，运算量也明显增大。而通过傅里叶变换[1]设计均衡器，不但在滤波的过程中具有很大的优越性，不存在相位误差、时间延迟这些问题，对调节多段均衡程序运算量上也有明显的减少。另外，这段程序是在TMS320DM642上进行的，该芯片的特点就是可以进行快速的乘法运算，因此，卷积等运算可以在芯片上高速的运行[2－3]。

1 设计原理

均衡器的基本功能就是调节信号各段频率的强弱，从而弥补信号在传输过程中的缺陷或是达到特定的声音处理效果。因此为了达到这个目的，调节信号的各段频率可以将输入的信号进行以下处理：

1）对输入的信号进行快速傅里叶变换，使得各个频段的信号分开；

2）对需要变化的频点及其周围的频点进行相应的处理；

3）将处理后的信号进行傅里叶反变换，得到最后需要的信号。

2 傅里叶变换

快速傅里叶变换[4－5]的时域抽取方法是将输入的信号按奇偶分开，打乱原来的顺序，之后进行蝶形运算，以保证输出的序列是按着时间顺序排列的。分解过程遵循两条规则：1）对时间进行偶奇分解，即码位倒置；2）对频率进行前后分解，即蝶形运算。

2.1 码位倒置

将长度为N的时域序列x（n）按n的奇偶分为两组，变成两个N/2序列

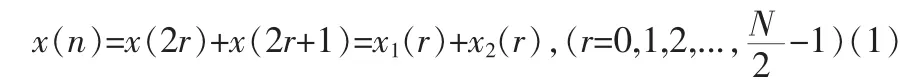
码位倒置可以将输入数据依照奇偶分开，如表1所示。

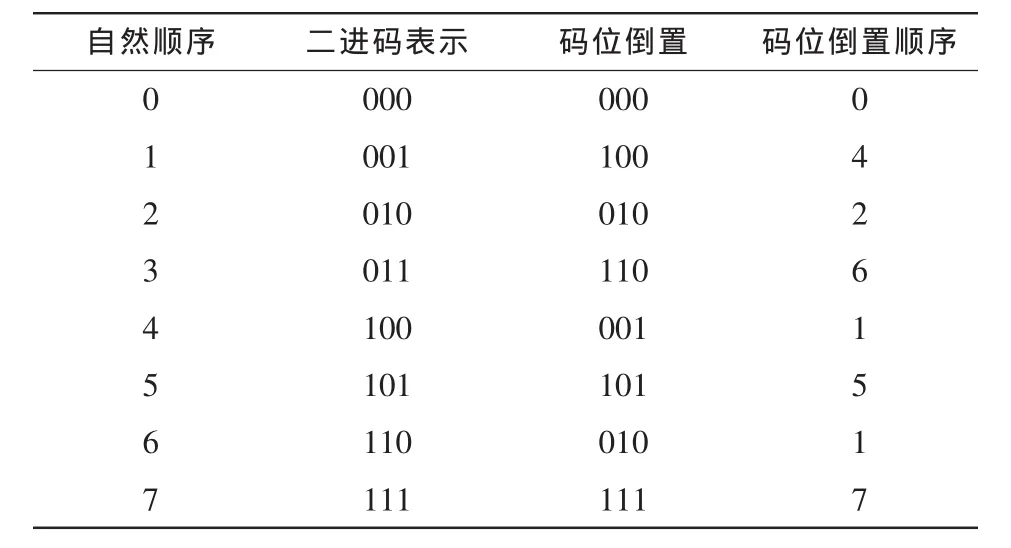
表1 码位倒置Tab.1 Code bit inversion

2.2 蝶形运算

2.2.1 蝶形运算的原理

蝶形变换是将处理的信号进行分级处理，逐次进行DFT变换，以减少复数的乘法减少运算次数。对于输入x（n）序列奇偶按分开的两个序列的DFT运算分别是

一个序列的DFT为

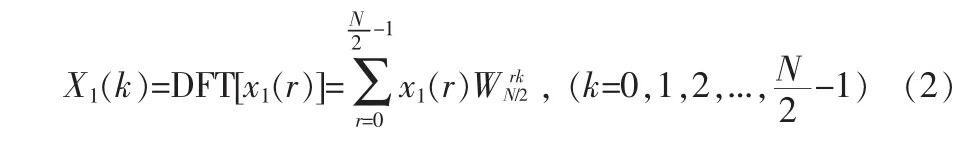
另一个序列的DFT为

蝶形运算的输入和输出：

2.2.2 蝶形运算的算法

蝶形运算是逐级运算累加实现的，在传统的蝶形运算中，旋转因子的N是保持一个固定的值而k是不断变化的，第一级到第级中，k的变化是以2为底的幂指数的变化，而到第级时，k 的变化则是 0,1，…，（N/2）－1。如果依照k的这种变化规律，在第级时，就很难继续依照前级进行变化。因此，根据以上分析，采用另外一种思路来对蝶形运算进行重新的整理。在旋转因子中，N是每个蝶形单元输入数据的个数，k的变化规律是0,1，…，（N/2）－1，采用这种方法就可以有效的缩短代码的长度，提高运行速度。图1为蝶形运算流程图。

2.3 快速傅里叶变换的实现

图1 蝶形运算流程图Fig.1 Flow chart of butterfly operation

Block=1；

for （BlockSize=2； BlockSize ＜=NumSamples； BlockSize＜＜=1） {

double delta_angle=angle_numerator/BlockSize；

s2=sin（－2*delta_angle）；

s1=sin（－delta_angle）；

c2=cos（－2*delta_angle）；

c1=cos（－delta_angle）；

w=2*cm1；

for（I=0； I＜ NumSamples； I+=BlockSize） {

r2=c2；

r1=c1；

i2=s2；

i1=s1；

for（j=I,n=0；n＜ BlockEnd；j++,n++）{

r0=w*r1– r2；

r2=r1；

r1=r0；

i0=w*i1– i2；

i2=i1；

i1=i0；

k=j+Block；

re=r0*RealOutData[k]– i0*ImagOutData[k]；

im=r0*ImagOutData[k]+i0*RealOutData[k]；

RealOutData[k]=RealOutData[j]– re；

ImagOutData[k]=ImagOutData[j]– im；

RealOutData[j]+=re；

ImagOutData[j]+=im；

}

}

BlockEnd=BlockSize；

}其中，Block是每一个蝶形单元输入个数的一半即N/2，r0和i0分别是旋转因子的实部和虚部。

3 均衡处理

对于频点的调节是调节频点周围这一段的频率幅度的大小，以最终达到调节频率的目的[6]。为了防止在抽取频点时，因某一点的调节范围过大而使这一段的声音听起来不和谐，在对频点进行调节时，采用的方法是调节该频点及其附近的频点以达到最终的调节效果。

算法的实现：取频率点周围的点，将所取的点调节的范围是该点与对应频率点的距离的反比，这样就避免该点频率的影响太强烈。算法流程如图2所示。针对某一个频点的处理的程序如下：

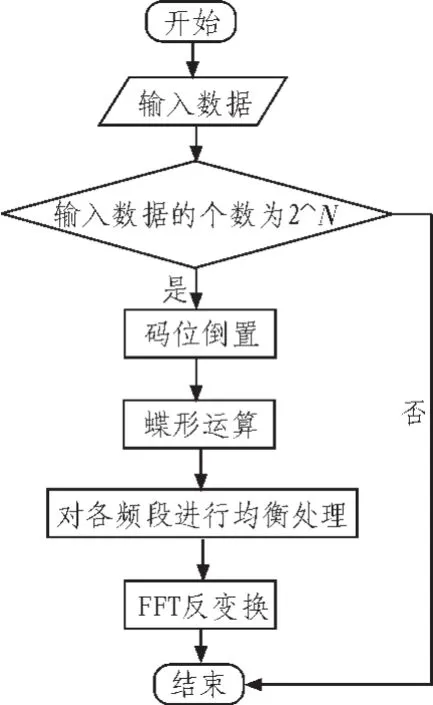
图2 算法流程图Fig.2 Flow chart of algorithm

a1=Mid-(i-1)；

a2=i-Mid；

RealOutData[i-1]=d*a2*RealOutData[i-1]；

ImagOutData[i-1]=d*a2*ImagOutData[i-1]；

RealOutData[i]=d*a1*RealOutData[i-1]；

ImagOutData[i]=d*a1*ImagOutData[i-1]；

Mid为调节频点对应的频率轴的位置，i为Mid相邻近的后面的点。

4 结束语

本文提出的采用频率滤波器对均衡器进行设计的方法，区别于其他的均衡器的实时滤波器的设计，既避免了IIR滤波器相位偏移的现象，又避免了FIR滤波器的延迟，因此对频率滤波具有很好的效果。另外，由于处理采用频域滤波，在处理音频信号时可以只经过一次傅里叶变换，就能处理各个频段的信号，大大减少了数据的运算量，因此使用频域滤波器可以更快捷、更高效地对数据进行处理。在使用该种方法进行滤波处理时，应注意采样点个数的选取，可以根据处理器缓存的大小决定采样点的个数，从而可达到更好的处理效果。

[1] 胡广书.数字信号处理[M].北京：清华大学出版社，2003:171-180.

[2] Texas Instruments.TMS320C6000 DSP Cache User’s Guide[EB/OL].2003.http://focus.ti.com/lit/ug/spru656a/spru656a.pdf.

[3] 王兴国，蒋伟峰，刘济林.使用TI专用音频DSP设计实时声效处理系统[J].电子技术应用， 1999，25（10）39-41.WANG Xing-guo， JIANG Wei-feng， LIU Ji-lin.Audio DSP design using the TI-specific real-time sound processing system [J].Application of Electronic Technique， 1999，25（10）:39-41.

[4] 称佩青.数字信号处理教程[M].2版.北京：清华大学出版社，2001:185-199.

[5] 董志，张羿猛，黄芝平，等.基于FFT流水线的快速实现方法与技术[J].测试技术学报，2009，23（5）:9-13.DONG Zhi， ZHANG Yi-meng， HUANG Zhi-ping， et al.Theory and application of FFT based on pipelined stream[J].Journal of Test and Measurement Technology，2009， 23（5）:9-13.

[6] 肖正安.基于Matlab的数字均衡器的设计[J].湖北第二师范学院学报，2008，25（8）:15-19.XIAO Zheng-an.The design of Matlab-based equalizer[J].Journal ofHubeiUniversity ofEducation，2008，25 （8）:15-19.