基于GSP拍卖和粒子群优化的AODV协议

张恒，郭超平

（1.陕西省商贸学校计算机教研室，陕西西安710065；2.西安通信学院陕西西安710106）

WMN（Wireless Mesh Networks）是一种给用户提供更好服务的无线网络，包含有两种节点：路由器（Mesh Router）和客户端（Mesh Client）。其中，路由器为客户端的业务进行路由转发；客户端除了要和其它客户端通信之外，还要转发其它客户端的业务。然而，转发其它客户端的业务需要消耗资源，如带宽和能量，付出一定的代价。因此，自私的客户端不情愿转发其它客户端的业务。在路由协议方面，文献[1-3]提出在WMN中使用修改的AODV路由协议，没有考虑到客户端的资源消耗情况。如何设计WMN的AODV路由协议，激励自私客户端参与业务转发，实现WMN的带宽与路由分配，仍是一个挑战。

针对上述问题，本文分析了WMN网络中自私客户端的理性行为，并将其建模为GSP拍卖模型，然后提出了基于GSP拍卖和粒子群优化的AODV路由协议，最后进行了总结。

1 相关工作

1.1 拍卖理论简述

拍卖机制（auction mechanism）是一组在非协作，竞争环境下对稀缺资源的分配规则：拍卖方（auctioneer）根据竞争者（bidder）对资源的出价（bid）决定他能获取的资源份额以及相关的支付（payment）。Vickery拍卖（也叫第二价格拍卖，second price auction）和GSP（generalized second price）拍卖是其中的两种。在Vickery拍卖中，胜利竞争者而造成的其他竞争者的代价差异决定了对他的支付。与Vickery拍卖相比，GSP拍卖只考虑仅次于考虑胜利竞争者的下一个竞争者的代价，它已被谷歌和雅虎用于因特网的广告拍卖[4]中。文献[2]指出Vickery拍卖能够保证竞争者的诚实性（Truth-telling），而GSP拍卖不能保证节点的诚实性。

拍卖已经被广泛地应用到自私多跳网络的路由：文献[5]提出在自私网络的路由时使用VCG拍卖进行带宽分配；文献[6]提出使用Vickery拍卖与自私行为斗争并促进网络间的合作；文献[7]首先提出了基于VCG拍卖的路由协议并指出VCG拍卖存在的overpayment问题，然后提出了基于第一价格拍卖的路由协议，其并没有给出两个参数和是如何取值的；文献[8]提出使用GSP拍卖实现多径多跳网络的路由，并没有给出保证节点诚实性的分配比例的取值方法。

1.2 自私节点代价函数的定义

在定义节点代价函数的时候，考虑到WMN中节点对哪些资源的消耗更为关注。文献[9]指出：路由器对于移动性和功率有效性基本没有限制，而客户端支持一定的移动性，需要支持功率有效性的路由协议。而客户端参与转发时最主要的是消耗自己的能量，这严重影响了它的寿命。为了激励自私客户端节点参与转发，源客户端支付给他一定的电子货币，每个客户端可用赚取的电子货币支付给转发自己业务的客户端。客户端主要任务是发送自己的业务，而不是赚取电子货币。在不同电子货币数量和能量时一个客户端转发其他客户端的倾向性是不同的：

1）当客户端的电子货币较多而能量较少时，转发其他客户端业务的代价较高，它不是很愿意转发其它客户端的业务；当客户端的电子货币较多而能量较多时，转发其它客户端业务的代价较低，它非常愿意转发其它客户端的业务。

2）当客户端的电子货币较少而能量较少时，转发其它客户端业务的代价非常高，它很不愿意转发其它客户端的业务；当客户端的电子货币较少而能量较多时，转发其它客户端业务的代价较高，它不很愿意转发其它客户端的业务。

总之，能量的重要性远大于电子货币。借鉴文献[6]的思想，代价函数的定义如下：

定义1当一个客户端vi在具有电子货币Ci和能量Ei的条件下，转发其它很业务量q而付出的代价与当前的能量Ei成反比，与当前电子货币Ci的对数和业务量q成正比，即：

这里，η为常量，作为一个参数在电子货币和能量之间的平衡因子，为了实现能量消耗均匀取值为16。在某一时间段内或某一时刻，可以认

1.3 粒子群算法综述

在粒子群算法[10]中，每个个体称为一个“粒子”，代表着一个潜在的解。例如，在一个H维的目标搜索空间中，每个粒子看成是空间的一个点。设群内由K个粒子构成。K也被称为群体规模。设γk=（γk1，γk2，…，γkH）为第k个粒子（k=1，2，…，K）的H维位置矢量，根据事先设定的适应值（与要解决的问题有关）计算γk当前的适应值，即可衡量粒子的位置优劣；λk=（λk1，λk2，…，λkH）为粒子的飞行速度，即粒子移动的距离；ρk=（ρk1，ρk2，…，ρkH）为粒子迄今为止搜索到的最优位置；ζk=（ζk1，ζk2，…，ζkH）为粒子迄今为止搜索到的最优位置。

在每次迭代中，粒子根据以下式子更新速度和位置：

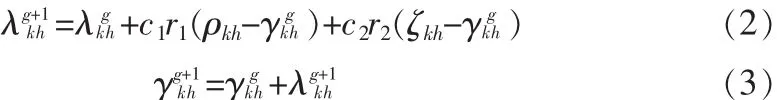
其中h=1，2，…，H，g是迭代次数，r1和r2为[0，1]之间的随机数，c1和c2为学习因子，使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点和群体最优点靠近。粒子根据它上一次迭代的速度、当前的位置和自身最好经验与群体最好经验之间的距离来更新速度；然后粒子根据式（3）飞向新的位置。为了改善粒子群的收敛性能，Shi和Eberhart引入惯性权式中[11]，即：

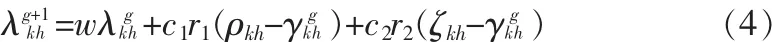
惯性权重起到权衡局部最优和全局最优能力的作用。其中，wmax为初始权重；wmin为最终权重，itermax为最大迭代次数。这样，粒子群算法在刚开始的时候倾向于开掘，然后逐渐转向开拓，从而在局部区域调整解。

2 AODV路由协议

2.1 系统模型

假设WMN由有限个节点组成，表示为G=（V，E），其中V=（v1，v2，…，vn）是n个节点组成，节点有两种类型：路由器和客户端；E=（e1，e2，…，el）是l条链路的集合。假设任意两个客户端或任意客户端－路由器对是可达的（即它们之间至少存在一条通信路径）。假设客户端是自私，理性而非串谋的，期望自己在转发其它客户端的业务时付出的代价尽可能小。

AODV路由协议是一个用于移动Ad hoc网络的主动式路由协议，并不能直接应用到WMN中，需要稍微修改即可。当源客户端S和目的客户端/路由器D（客户端和路由器通信的目的是希望和Internet等通信）之间有一个带宽为q的业务请求，它广播路由请求分组RREQ（Route Request Packet）。每个收到RREQ的中间客户端/路由器，如果收到的RREQ不是前面收到的RREQ的复制，在增加跳数之后广播这个RREQ。当目的客户端/路由器D收到这个RREQ后，产生一个路由应答分组RREP（Route Reply Packet）并按来时路由单播回去，一直到S。在返回RREP的过程中，中间客户端vi将系数fi和可用带宽bi加密后一起添加RREP中，而中间路由器ri添加自己的可用带宽bi（其代价函数为0）。对于客户端vi，代价函数fi和可用带宽bi构成了vi的类型ti=＜fi，bi＞。假设经过路由发现之后，S和D之间不相交的每条路径包含客户端的路径集合为P={P1，P2，…，Pm}，不相交的每条路径上节点全为包含路由器的路径集合为P={P1，P2，…，Pd}。

S要给予中间客户端一定的支付以激励它们参与业务的转发，并且这个支付要大于它付出的代价。在这个博弈中，每个vi选择一个行动ai，这个行动是宣布它的当前可用带宽和代价函数。因此，参与人的行动决定了代价函数fi（zi）和支付函数pi。因此，vi的效用函数是：

每个中间客户端的目标是最大化自己的效用函数，而源客户端S的目标是通过在这m条路径之间合理地分配带宽和路由使总的代价最小化。令P和P’中路径Pj可用带宽为Bj=min{bi|vi∈Pj∪ri∈Pj}，P’总的可用带宽中路径Pj的代价函数Pj的带宽为zj。假设q＞BP′，需要P中路径提供的带宽为（q－BP′）。这样的系统模型为拍卖模型，表示为：

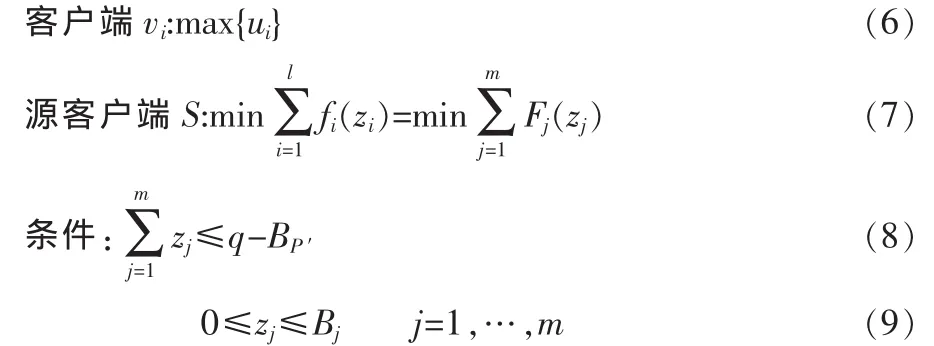
2.1.1 给予中间mesh客户端vMCi的支付

S要给予vi一定的支付以激励它们参与业务的转发。本文采用GSP拍卖，在S收到所有RREP以后，计算出P中每条路径的代价并按照从小到大的顺序进行排序，集合P变为LCP={PLCP1，PLCP2，…，PLCPm}（对于s≤t，那么Fs≤Ft）。如果客户端vi位于PLCPj，那么给予客户端vi的支付为：

2.1.2 附加约束条件

为了保证参与客户端的诚实性，参与带宽分配的路径数和每条路径分配的带宽必须满足一定的条件[8]：

1）P中参与带宽分配的路径数小于P的路径总数，假设有m个（m′＜m）路径参与带宽分配。

2）每条路径分配的带宽占P中所有参与带宽分配的路径的分配带宽总和的比例满足以下限制，对于任意s＜t，（Fs+1－

对上述不等式的两边同乘Fs）zt，从而系统模型变为GSP拍卖模型，即：

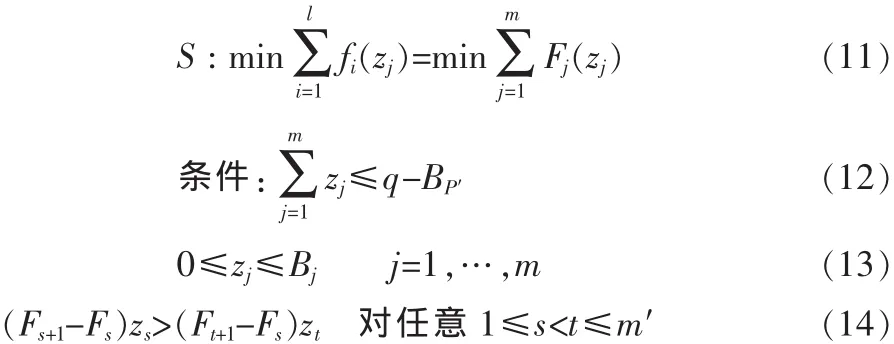
式（14）是模型的诚实性保证。显然式（11）～（14）为一凸优化问题，直接用凸优化的方法进行求解可获得带宽和路由分配的结果，但是这样会带来大量的计算，尤其是（14）式。采用粒子群算法对上述的问题求解进行优化，可快速找到最佳分配结果。

2.2 基于GSP拍卖和粒子群优化的AODV路由分配算法

源客户端S在收到所有RREP后，运行基于GSP拍卖和粒子群优化的AODV路由分配算法。利用粒子群优化算法，可以快速找到满足限制条件的最优解，加快算法的收敛速度。

算法描述如下：源客户端首先将从S到D的所有路径分为两个集合P和P′，计算P′中每条路径的可用带宽及其和BP′。然后S判断P′中各条路径的可用带宽之和BP′是否大于等于q，如果是，算法结束，否则算法继续。接着，计算P中每条路径的代价函数和可用带宽，并对P中每条路路径按照路径代价从小到大的顺序进行排序，得到最小代价路径集合LCP。然后，选出LCP中的前面m′条路径，可用带宽之和大于等于（q－BP′）。最后，S利用粒子群优化算法对式（11）～（12）求解；如果无解，将m′加1，重新求解，这样一直到求得最优解。算法的伪代码如下：

算法1利用粒子算法求解的基于GSP拍卖的路由分配算法

输入：P中每条路径的所有节点的可用带宽和代价函数，P′中每条路径的所有节点的可用带宽。

输出：P和P′中每条路径的分配的带宽以及所有节点的的支付。

步骤2：计算P中路径Pj的代价Fj，按照Fj从小到大的顺序将P中的路径排序，得到LCP；从LCP中选取前面m′条路径，使其可用带宽之和满足不小于（q-BP′）。

步骤3：c1=c2=2；wmax=0.9，wmin=0.4，max_gen=100，初始化

步骤5：如m′加1，返回步骤4；否则输出这m′条路径以及步骤1中分配的结果。

3 结论

本文分析了自私WMN网络中mesh客户端的理性行为，并将其建模为GSP拍卖模型。然后提出了基于GSP拍卖和粒子群优化的AODV路由协议。此算法收敛速度较快，可以直接在客户端侧实现，协议简单，可对AODV协议稍微修改就可应用到WMN中去。

[1]KONG Peng-yong，WANG Hai-guang，GE Yu，et al.A performance comparision of routing protocols for maritime wireless mesh networks[C]//IEEE.WCNC 2008，2008:2170－2175.

[2]XIAN Xiao-dong，FU Yun-qing，WANG Song-jian，et al.A routing protocol based on combinative metric for wireless mesh networks[C]//IEEE.ICNS 2009，2009:803－806.

[3]Pirzada A A，Wishart R，Portmann M.Multi-linked AODV routing for wireless mesh networks[C]//IEEE.Globecom 2007，2007:4925－4930.

[4]Edelman B，Ostrovsky M，Schwarz M.Internet advertising and the generalized second price auction:selling billions of dollars worth of keywords，american economic review No.1917[R].Stanford：Stanford Graduate School of Business，2007.

[5]WU Fan，ZHONG Sheng，LIU Ji-qiang，et al.Cost-effective traffic assignment for multipath routing in selfsih networks[C]//IEEE.GLOBECOM 2007，2007:453－457.

[6]Demir C，Comaniciu C.An auction based AODV protocol for mobile ad hoc networks with selfish nodes[C]//IEEE.ICC 2007，2007:3351－3356.

[7]WANG Yu，WANG Weizhao，Dahlberg T A.Truthful routing for wireless hybrid networks[C]//IEEE.GLOBECOM 2005，2005:3461–3465.

[8]Xueyuan S，Chan S，Peng G.Auction in multi-path multihop routing[J].IEEE Communications Letters，2009，13（2）:154-156.

[9]Ian F.Akyildiz，Xudong W.A survey on wireless mesh networks[J].IEEE Communications Magazine，2005，43（9）:523-530.

[10]Kennedy J，Eberbart R C.Particle swarm optimization[C]//IEEE.Proceeding of IEEE International Conference on Neural Networks，1995:1942-1948.

[11]Shi Y，Eberbart R C.A modified particle swarm optimizer[C]//IEEE.Proceeding of IEEE International Conference on Evolutionary Computation，Anchorage.1998:69-73.