一种柔性曲柄滑块机构的解耦控制方法

党小宝，张建花，王沙威

（中国飞行试验研究院陕西西安710089）

柔性连杆机构运动时，长径比较大的构件会发生显著的弹性变形和剧烈的弹性振动。对机构的运行精度和使用寿命都有很大影响。应用于航天飞机上的机械臂、空间站上的大型可展天线、太阳能帆板等系统，其变形对于定位、操作及运动稳定性都有严重的影响。所以，考虑机构中的柔性影响并利用控制方法抑制其影响成为一个被广泛关注的领域。

柔性机构的控制主要分为以下4类[1-4]：1）基于运动学模型的控制策略，该策略假设末端执行器位移的微小变化与驱动器位移的微小变化呈线性关系.根据运动学方程计算出与机构输出位移微小增量相对应的驱动器位移连续的微小增量，但这类控制策略并未考虑并联机构的强耦合、非线性的动力学特性，只适合速度和精度要求不高的应用场合；2）基于动力学模型的控制策略，该类控制策略根据机构运动输出的要求，依靠动力学逆模型的求解得到驱动力的控制向量作为开环控制量，这类控制策略的弱点是不能在有效载荷发生变化时改变反馈增益，并且求解柔性逆动力学存在着解的存在性和唯一性不能满足、计算效率低等问题；3）基于性能的控制策略，这类控制不需要依赖于精确的被控对象模型及负载参数，而是通过控制器的设计技巧来获得良好的控制效果以及鲁棒性，这类控制器包括自适应控制，变结构控制和鲁棒控制等；4）冗余驱动控制，可以改善甚至消除工作空间中的奇异位形，解决奇异点导致的运动精度降低、刚度减小和驱动关节无法实施控制等问题，但由于冗余驱动力的存在同样使得逆动力学方程的唯一性无法保证，增加了控制难度。

针对含柔性体的机构特点，即目标运动由快变的弹性小变形和慢变的刚体大范围运动组成，本文提出了一种基于解耦的控制方法，这种方法有效利用了模型信息，将反馈划分为由刚性和柔性影响产生的运动两路反馈，通过两组不同的控制器分别计算各自的输出量，并在控制器输出端叠加输出。

文章针对曲柄滑块机构进行了柔性动力学建模并实施了轨迹跟踪仿真。与同样基于动力学模型的计算力矩法进行了对比，证明本方法获得了良好的效果。

1 曲柄滑块动力学模型建立

曲柄滑块机构在机械和航空工程中得到广泛的应用，所以它的动力学建模的准确性有很重要的意义。通常情况下，曲柄滑块机构的曲柄被设计为短而粗的构件，所以可以被看作刚体处理。而连杆一般根据需要被设计为一个刚度较小的细直杆，所以应该考虑柔性对整个机构运动的影响。曲柄滑块机构如图1所示。

20世纪90年代后期至今，有关连杆柔性的建模中文献[5-7]，大多采用了KED（运动弹性动力学）方法进行建模，由于没有考虑弹性和刚体位移之间的耦合，所以建立的数学模型不够精确。文献[8]中，考虑了弹性位移和刚体位移间的耦合，并考虑了运动副摩擦。文中将连杆看作为弹性梁，根据模态截断准则取连杆的前二阶模态函数描述变形，最后通过Lagrange第二方程导出曲柄滑块机构的动力学数学模型。然而它的不足是：首先，由于柔性多体系统是非线性变结构系统，各部件经历高速运动时，部件和系统的近似特征频谱和模态都将是时变的，模态截断的准则还有待于研究，不能简单取前N阶模态；其次，由于仅取了前二阶模态，所以在精确性上还可以提高。

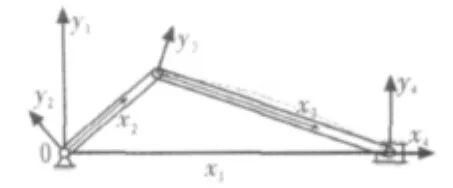
图1 曲柄滑块机构Fig.1Crank-slider

基于此，本文同样将曲柄和滑块视作刚体，而将连杆看作弹性梁，使用有限单元法对弹性变形进行离散化，而根据所需精度的要求划分单元数。最后，通过拉格朗日第二方程建立了曲柄滑块机构的动力学数学模型，所得到的数学模型能够准确的描述曲柄滑块机构的真实动力学行为。

为了简化方程推导，本文将连杆作为一个梁单元处理。

根据运动及变形特点，选取未变形时连杆的两端点A、B的连线为动坐标系的X轴，建立Y轴构成右手坐标系，如图2所示。

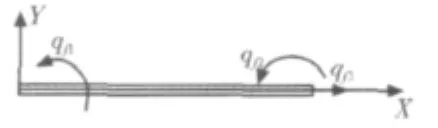
图2 弹性连杆Fig.2Elastic rod

于是连杆相对于动坐标系的弹性变形运动相当于一个简支梁的振动，其形函数为：

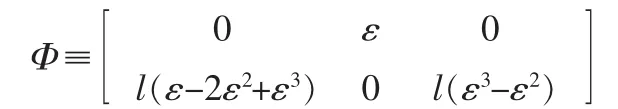
令描述相对于动坐标系变形的广义坐标为qf=[qf1qf2qf3]T，其中，qf1为A点处的转角，qf2为B点处的x方向位移，qf3为B点处转角。

设曲柄OA相对于x1轴的角坐标为θ，于是描述系统的广义坐标共有4个，即：

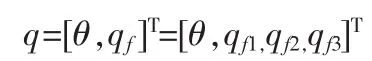
采用拉格朗日第二方程：

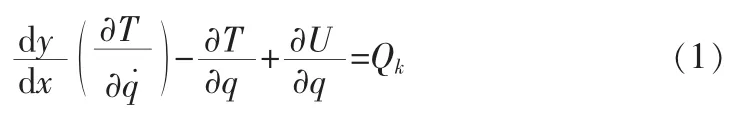
来建立机构的动力学数学模型。

为此，先构造出动能：

其中T1为曲柄动能，T2为连杆动能，T3为滑块动能。

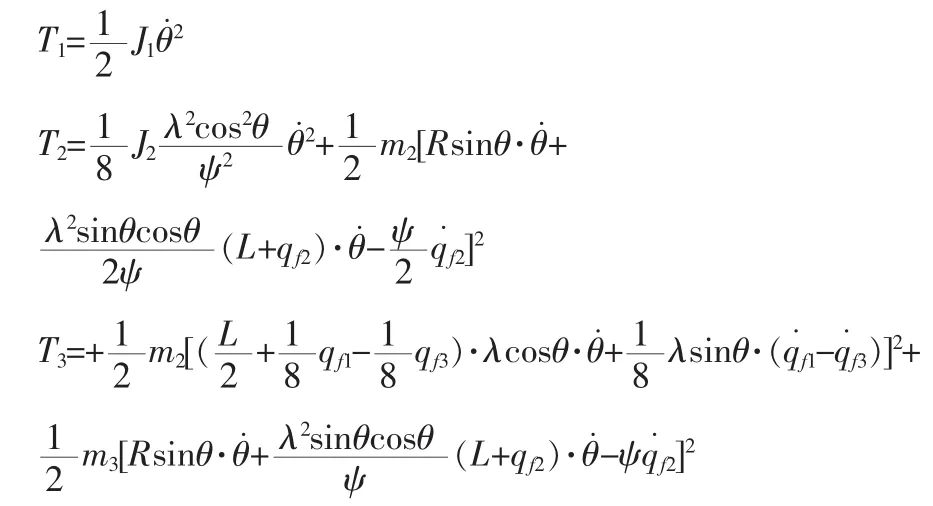
势能由弹性势能和重力势能两部分组成：

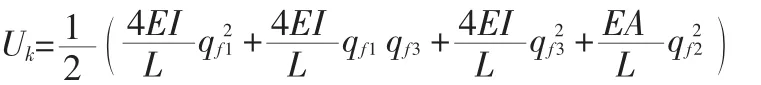
Qk为非保守力对应的广义力，本例中取电机的驱动力矩τ。将式（2），（3）代入式（1），得到二阶微分方程组：

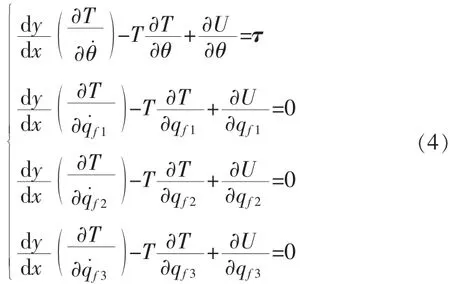
方程（4）就是考虑连杆柔性情况下所建立的曲柄滑块的动力学方程，在得到该方程的基础上，结合运动的初始条件，用数值方法（纽马克β法）求解该方程，则可得到机构的运动响应。

2 解耦PID控制方法

以往的多柔体机构控制研究中，经常选取主动件的运动作为控制目标。在曲柄滑块机构中，即选取曲柄作为控制对象，使其角位移、角速度、角加速度满足理想的轨迹要求。但在实际应用中，往往我们需要的是从动件满足某种特定的轨迹运动。在曲柄滑块机构中，工程中经常以滑块的运动速度为目标，要求其匀速稳定运动或是满足平稳启动及平稳停止。这时，因为主动件和从动件间并不是由刚体而是由柔性体相连接，柔体的特性如振动和相位滞后等将使机构的控制难度增加。

柔性体上任一点P的位置向量为

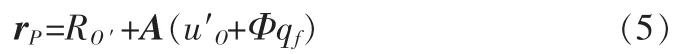
其中A为主动旋转变换矩阵，RO′为动坐标系位置向量，u′O为P点在动坐标系的位置向量，Φ为形函数，qf为描述变形的广义坐标。

于是P点的速度向量为：

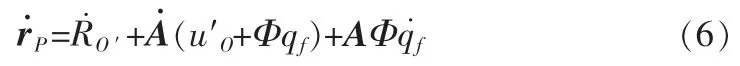
考虑柔性体的运动可以看作是由快变的弹性变形和慢变的刚体运动组成，如果简单的使用一个控制器，由于调节频率和幅度相互影响，会使控制结果或趋于不稳定，或者达不到抑制柔性振动的效果。

如果能够将主动件和从动件间的相互运动分解为低频的刚性运动和高频的柔性运动，那么分别使用两个不同的PID控制器去分别控制慢变的刚体大范围运动和快变的弹性小变形运动，这样，两个控制器的控制效果都将满足各自要求，而在输出端，我们只须将两者的控制输出信号叠加，即可得到需要的控制力矩。

将P点位置分解为

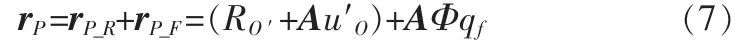
其中rP_R=（RO′+Au′O），不含与描述弹性变形的广义坐标qf有关的向量，并且从数值上与多刚体动力学模型中的对应项相同，所以被认为是柔性体运动中描述刚性运动的部分。rP_F=AΦqf，则是柔性体运动中除去刚性运动的部分，显然，它与描述弹性变形的广义坐标qf相关，所以被近似认为是描述柔性的部分。

在实际的应用中，由rP_F=rP-rP_R，而rP_R可以由刚体运动学方程简单的计算出，使得认为区分刚性和柔性成为可能。

当既可以获得主动件的运动反馈，又可获得从动件的运动反馈，基于简单的多刚体的动力学模型，可以按照上面的分解方法分别得到两个控制器的反馈输出。

从另一个角度看，刚柔分离的实质是建立在浮动坐标系的理论基础上，刚性部分是描述目标点随浮动坐标系的运动，而柔性部分描述的是目标点在浮动坐标系内的变形运动。然而可以看到，柔性部分因为含有主动旋转变换矩阵A，而A是θ的函数，所以这种分解并未达到刚柔的完全解耦。但是从仿真结果可以看出，其控制精度已经满足要求。

针对曲柄滑块机构而言，由于滑块和曲柄是由柔性体连杆连接的则可以将滑块位移分为

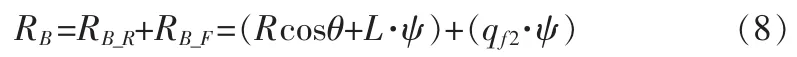
使用两个简单的PID控制器来处理此问题。令控制器方程为：

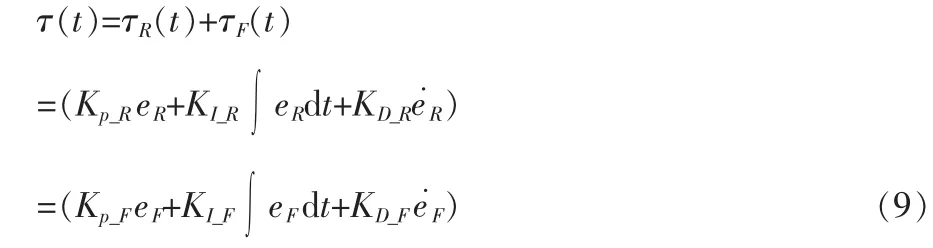
RP_R控制器的误差反馈，其中为理想轨迹。eF=－rP_F为柔性控制的误差反馈。控制流程如图3所示。

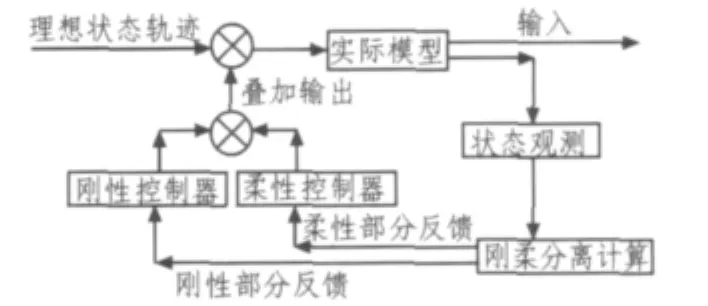
图3 控制流程图Fig.3Flow chart of control

文献[10]中，利用李亚普诺夫方法，对于机构的PID控制稳定性有系统详细的论述。并得到稳定性定理：

对于一个输入的角位移θ，机构的动能应当是有界的正实数，动能对于广义坐标的微分应当是有界的，势能也应当是有界的，即满足存在4个正常数a1，a2，a3，u，满足：

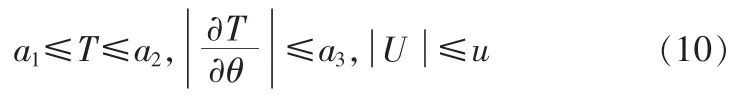
假设理想速度和加速度是有界的，即存在两个正常数

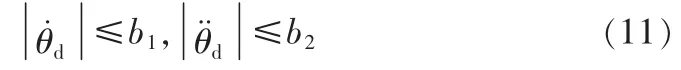
若kp和kd以及常数ε满足以下条件：

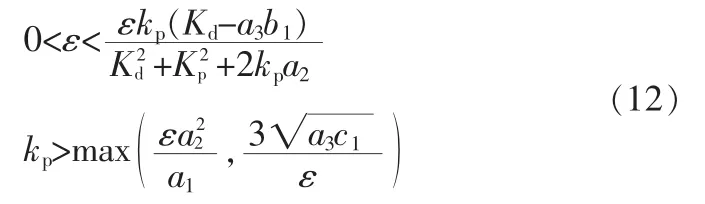
则，轨迹跟踪误差可以被限制在：

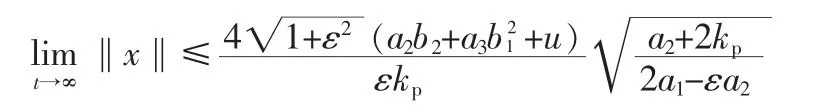
所以，PID控制虽然不能达到渐近稳定，但是在一定条件下可以将误差控制在一定范围内。这对控制器的参数的选取提出了相应要求。在这里使用优化的方法，以PID控制器的3个参数kp，ki，kd为设计变量，跟踪轨迹与理想轨迹的RMS为目标函数，上面定理中的各条件（10），（11），（12）为约束条件进行优化，即可以得到最优的控制参数值。

3 仿真

为了验证这种控制方法的有效性，将曲柄滑块机构作为研究对象，通过MATLAB进行了数值仿真。

如图1所示的曲柄滑块机构中r=0.5 m，L=1 m，m1=3.51 kg，m2=1.86 kg，m3=5.5 kg，I=6.75×10－8m4，g=9.8 m/s2，E=1 GPa。

机构的初始条件为：

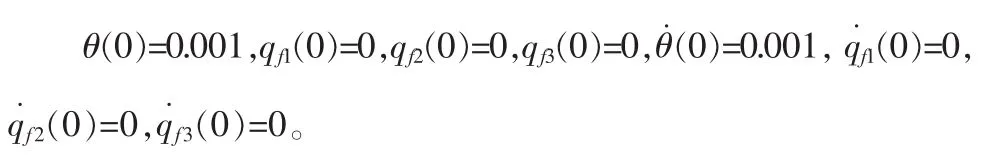
位置控制要求滑块满足匀速运动，即在4 s内使滑块从初始位置RB（0）=1.5匀速运动至RB（4）=0.7处。理想曲线如图4中虚线表示。

控制器参数取为：

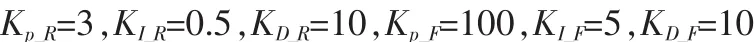
作为对比，应用计算力矩法进行仿真，其外层控制器参数取：

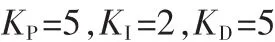
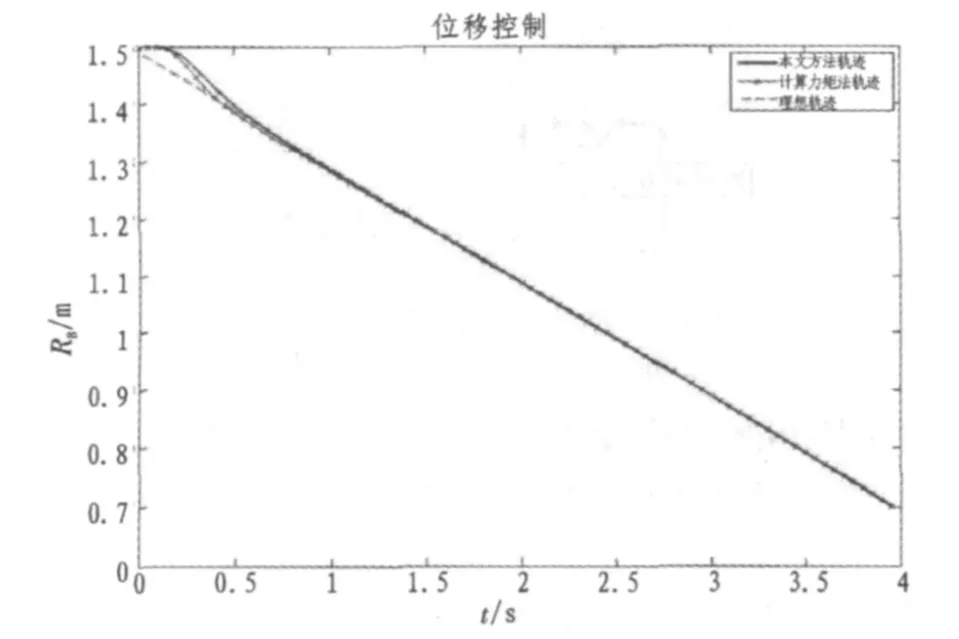
图4 控制效果Fig.4Control effect

图4中，带十字标记的为应用计算力矩法得到的轨迹跟踪曲线，粗实线表示应用本文方法得到的轨迹曲线。可以看到，在仿真时间等于0.7 s时本文方法的控制输出达到要求，并且有较好的稳态效果。但相对于计算力矩法的稳定时间（0.5 s）较长。

图5是本文方法中涉及柔性部分的控制效果，可以看到，通过柔性控制器的作用，把柔性产生的误差控制在了0.5×10-6m范围内，达到了很好的抑制振动的效果。

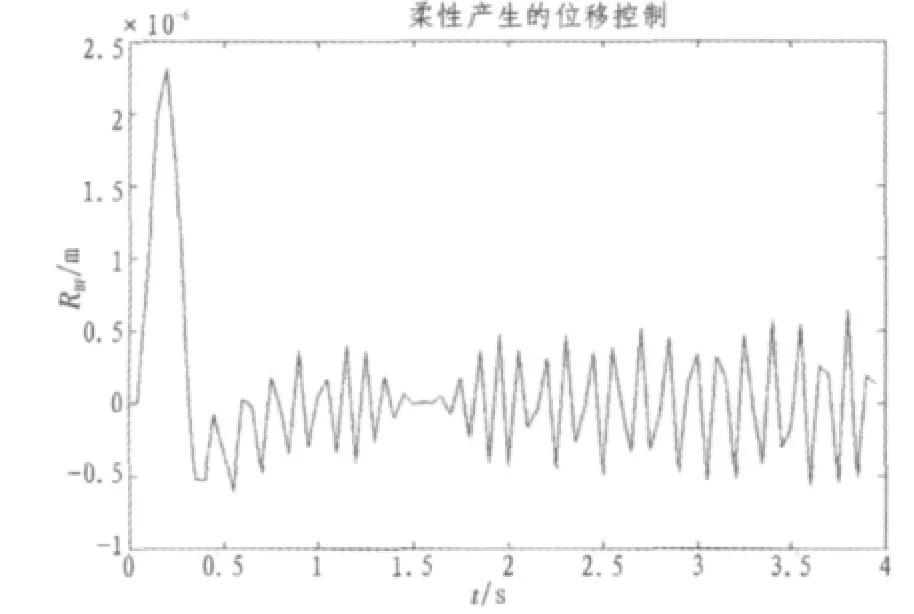
图5 振动抑制效果Fig.5Vibration suppression effect

图6，图7为跟踪正弦曲线的效果图。

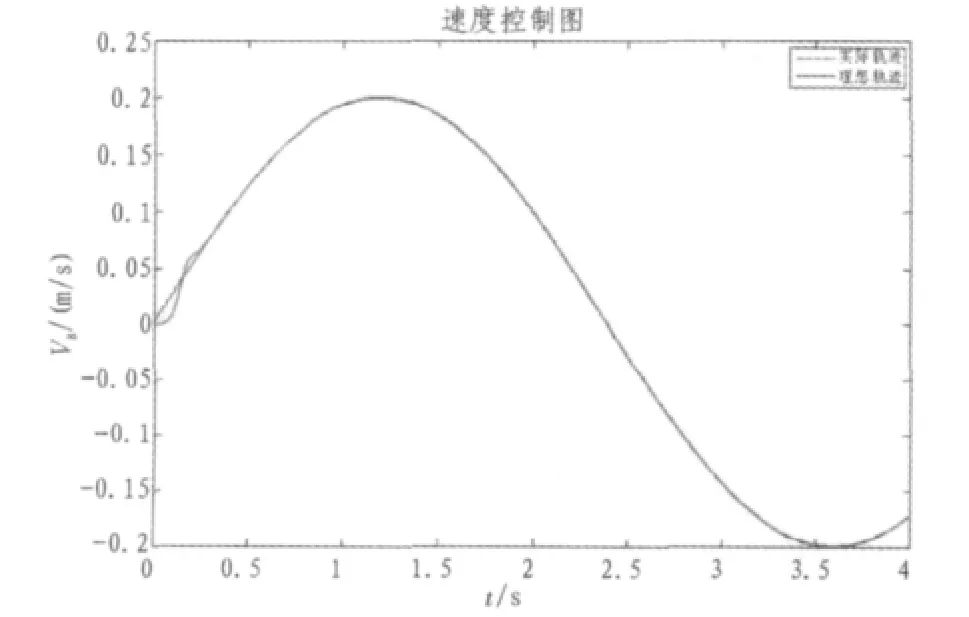
图6 跟踪正弦曲线Fig.6Sinusoidal tracking

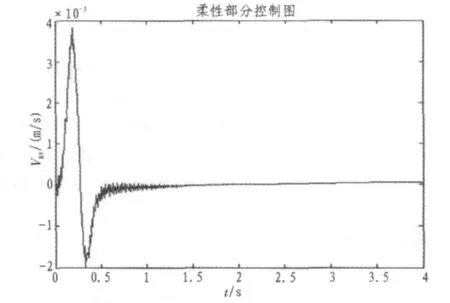
图7 振动抑制效果Fig.7Vibration suppression effect

4 结论

本文基于对柔性运动学和动力学模型的分析与分解，提出了一种针对柔性曲柄滑块机构的解耦控制方法，针对曲柄滑块机构进行位置跟踪控制，获得良好的效果。与同样基于动力学模型的计算力矩法进行对比发现，在控制效果相近的情况下，本文方法避免了计算力矩法中计算柔性体逆动力学会遇到的各种问题，大大提高了效率。

虽然该方法获得了较好的控制效果，但并未从完全对目标运动进行解耦，这也将是下一步我们将深入研究的问题。

[1]LI S J，FENG Z，FANG H.Variable structure control for 6-6parallelmanipulatorsbasedoncascadedCMAC[C]//Proceedings of the 4thWorld Congress on Intelligent Control and Automation，Shanghai:IEEE，2002：1939-1943.

[2]Kock S，Schumacher W.A parallel x-y manipulator with actuation redundancy for high-speed and active-stiffness application[C]//Proceedings of the 1998 IEEE International Conference on Robotics and Automation.Leuven:IEEE，1998:2295-2300.

[3]Marquet F，Krut S，Pierrot F.Enhancing parallel robots accuracy with redundant sensors[C]//Proceedings of 2002 IEEE International Conference on Robotics and Automation，Washington DC:IEEE，2002：4114-4119.

[4]罗磊，莫锦秋，王石刚，等.并联机构动力学建模和控制方法分析[J].上海交通大学学报，2005，39（1）:274-276.LUO Lei，MO Jin-qiu，WANG Shi-gang，et al.Parallel manipulator dynamics modeling and control[J].Shanghai Jiaotong University，2005，39（1）:274-276.

[5]Fallahi B，Lai S，Venkat C.A finite element formulation of a flexible slider-crank mechanism using local coordinate[J].ASME J of Dynamic Systems，Measurement&Control，1995，117（3）:329-338.

[6]Lieh J.Separated-form equations of motion of controlled flexible multibody systems[J].ASME J of Dynamic Systems，Measurement&Control，1994，116（4）:702－712.

[7]Chu S C.Dynamic response of a high-speed slider-crank mechanism with an elastic connecting rod[J].ASME J of Engineering for Industry，1975（97B）:542－550.

[8]张劲夫，许庆余，张陵.考虑连杆柔性和运动副粘性摩擦的曲柄滑块机构的动力学建模及计算[J].航空学报，2001，22（3）:75－78.ZHANG Jin-fu，XU Qing-yu，ZHANG Ling.Vice-link flexible and take into account viscous friction of the crank motion slider mechanism of dynamic modeling and calculation of aviation 2001，22（3）:75－78.

[9]Asada H，Ma Z D.Inverse dynamics of flexible robots——modeling and recursive computation using virtual rigid link coordinate systems[C]//American Control Conference，USA:Pittsburgh，1989:2352－2359.

[10]WU F X，ZHANG W J，LI Q.Ouyang integrates design and PD control of high-speed closed-loop mechanisms[J].ASME J of Dynamic Systems，Measurement&Control，2002，124（1）:522－528.