基于Gardner算法的抗载波偏差的一种改进算法

杨帆，林平分

（北京工业大学嵌入式重点实验室，北京100124）

在数字通信系统中，接收端设备为了保持采样时钟与接收到的信号互相同步，必须计算采样时间与信号上的最佳采样点之间的时间差，即采样时钟偏差τ，并且跟踪这个τ，使得τ保持在足够小的范围内。TED（Timing Error Detector）就是计算采样时钟偏差τ的模块。TED模块只负责计算出这个采样时钟偏差τ，然后由PLL等模块负责把该时钟偏差纠正过来，从而实现发送和接收的同步采样。

Gardner算法[1]是数字通信接受端上被广泛使用的一种TED（Timing Error Detector）算法，它拥有实现简单、硬件消耗较小、精确度高、对相位偏差不敏感的特点。但是这个算法的可行性有一定的前提：即假设每个采样值的相位偏差不变，也就是说没有载波偏差。当假设条件不满足时，算法的性能将会受到影响，可能无法达到系统的性能要求。为了解决这个问题，本文提出了一种基于Gardner算法的改进算法，该算法可以在载波偏差存在的情况下工作，并且表现出接近无载波偏差时的性能，提高了原算法的可靠性和准确度。此外还对改进的算法进行了仿真和验证，并列出了仿真结果，仿真结果证明改进后的算法在载波偏差处于一定范围时，可以提高原算法的精确度30%~93%。

1 原理描述与数学证明

Gardner算法在每个符号周期T内只需要采样2次。改进算法只增加了一个计算模块和一个乘法器，如图1所示。

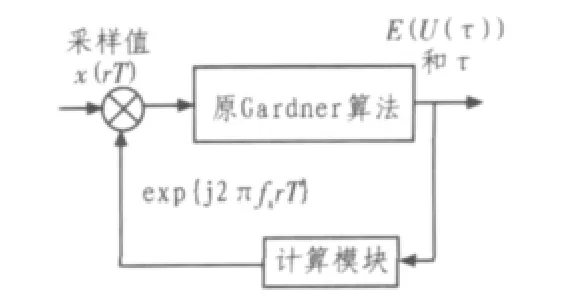
图1 改进后的算法结构Fig.1The improved algorithm’sstructure

图1中，{x（rT）}是采样后的信号，如果{x（rT）}不带有载波偏差，经过原Gardner算法模块，输出是{E（U（τ））}值，在采样信号平均功率既定的条件下，{E（U（τ））}与τ满足确定的对应关系，由这个关系函数可以计算出τ的值，再把τ输出给纠正采样时钟偏差的模块，完成纠正任务，同时TED会不断重复计算{E（U（τ））}的值来跟踪τ的变化。如果{x（rT）}带有载波偏差，{E（U（τ））}与τ的对应关系改变。改变后的对应关系没有使{E（U（τ））}失去计算出τ的能力，而是使得{E（U（τ））}计算出τ的精确度变差。精确度变差会影响TED跟踪τ值的能力。为了在载波偏差存在的情况下得到较好的精确度，改进后的算法给采样信号乘上一个辐角随序列号r线性增加的函数，如图1中的exp{j2πfarT}，这个乘法相当于给采样信号做了一个跨度为fa的频谱搬移。载波偏差的增加对Gardner算法精确度的影响不是线性增加的，也就是说并非载波偏差越大，对精确度的影响就越大。载波偏差的增加对Gardner算法的精确度的影响是周期变化的，后文会证明出这个周期是，所以当载波偏差是的倍数时，Gardner算法的精确度会表现得接近于没有载波偏差，不需要计算出载波偏差本身，只需要计算出载波偏差与最临近的的倍数的差值，再把采样信号在频域上搬移这个差值，这样相当于把载波偏差搬移到对精确度影响最小的区间。这样就使得在载波偏差存在的情况下，τ的计算拥有更好的精确度。

计算模块的任务是由图1中的{E（U（τ））}序列和τ序列计算出搬移距离fa的中间变量，乘法器的任务是把采样信号做跨度为fa的搬移。

采样之前的信号中，每一个符号所持续的时间T内有一个最佳采样点，Gardner算法要求在每个预计的最佳采样点上采样，并且在每两个最佳采样点之间的时间段的正中央采样，每个符号周期内采样2次[2]。预计的最佳采样点与真实的最佳采样点之间的时间差即为采样时钟偏差τ。

用r代表符号序列，用{x1（rT）}和{xQ（rT）}来表示在第r个符号周期内最佳采样点上的采样

之间的时间段的正中央的采样值。其中{x1（rT）}、{xQ（rT）}，（r∈N）即采样得到的数字信号，将被TED以外的其他模块所使用。据。Gardner算法的表达式是：

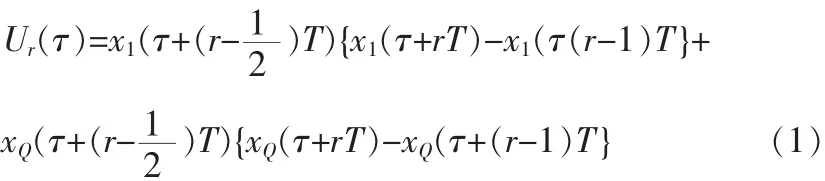
当采样时钟偏差为零，即τ=0时，有：

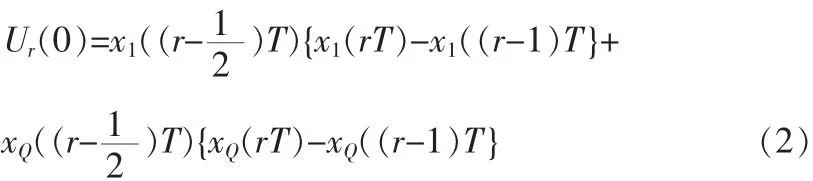
为了论述简洁，不妨只针对路信号论述，

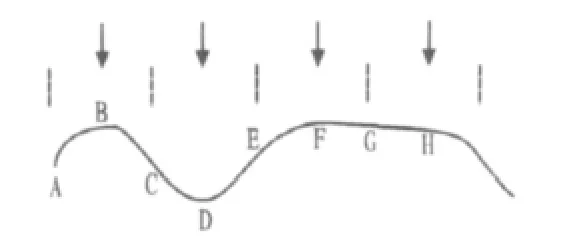
图2 信号的采样时间Fig.2Sample time on the signal

图2摘自文献[2]。图2中黑色箭头所指的位置：B点、D、F、H点表示最佳采样点，即{x1（rT）}，（r∈N）；黑色竖线所指的位置：A、C、E、G点表号大小的单位时，不妨认为x1（B）=1，x1（D）=1，x1（F）=x1（H）=1，x1（A）=x1（C）=x1（E）=0显然可得:

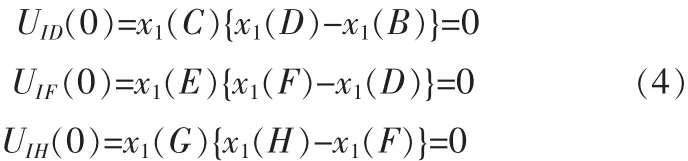
即在信号由1翻转为-1、由-1翻转为1、不翻转这3种情况下{UIr（0）}的值都是0。这个结论也适用于{UIQ（0）}，即在τ=0的情况下有Ur（0）=UIr（0）+UQr（0）=0。在τ偏离0的时候，{Ur（0）}也偏离0，偏离大小随翻转情况不同而不同。由于信号翻转情况的概率服从既定的分布率的[3]，{Ur（0）}的统计均值{E（Ur（0））}在τ偏离0时的值是可以确定的。Gardner的论文[1]中已经详尽证明，在相位偏差不变、经过接收机滤波后的符号脉冲为偶函数、信号带宽超过采样频率40~100%的条件下，

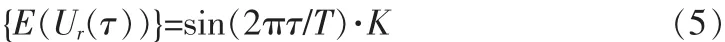
由于{E（Ur（0））}是统计均值，已经与具体的符号序列无关，所以略去脚标r。K是由采样频率、符号脉冲在频域的形状所决定的一个值[4-6]，在符号脉冲和采样频率确定时，K可以视为常量。所以得到{E（Ur（τ））}随τ变化的函数图形如图3所示。

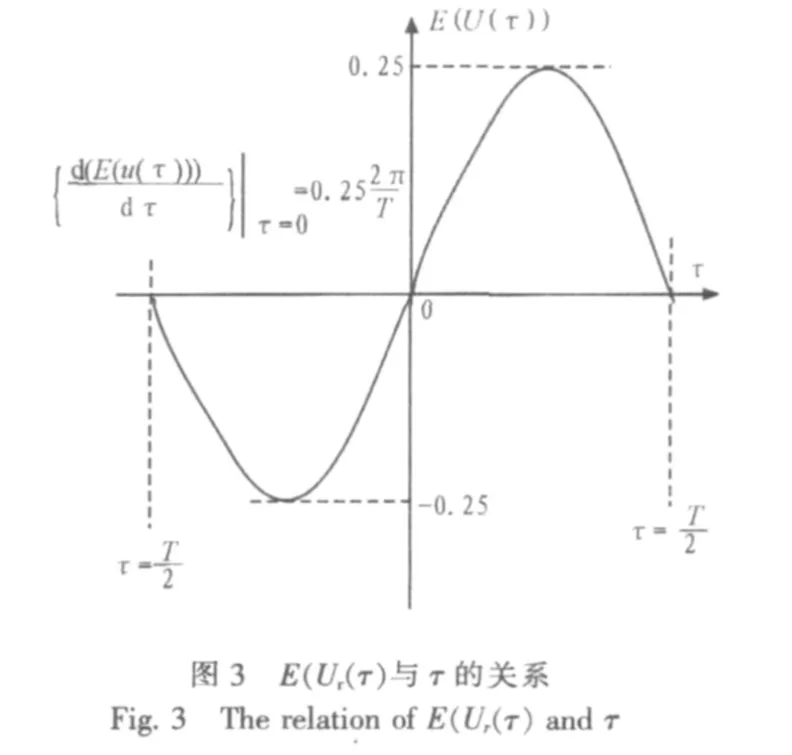
由于{E（Ur（τ））}显然是周期为T的周期函数，图3中只给最佳采样点的采样值的能量归一化为1时，{E（U（τ））}函数图形在τ=0处的斜率最大值0.25，最小值-0.25。{E（U（τ））}函数在τ=0处的导数代表了这个TED算法的精确度。因为TED模块是用{E（U（τ））}的值来估计τ的值的，在信噪比一定的情况下，TED模块可分辨{E（U（τ））}的值的精度就是一定的，设这个精度值是Δ{E（U（τ））}，确定Δ{E（U（τ））}的值在τ=0附近对应的Δτ也是确定的。TED模块可以分辨的最小的Δτ可以这样计算出来：

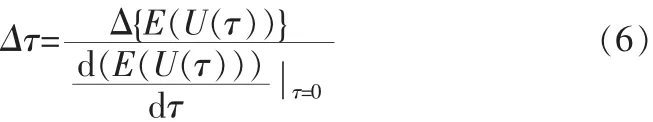
所以，信噪比一定的情况下，{E（U（τ））}函数在τ=0处的导数越大，TED模块可分辨的最小值Δτ越小，精确度也就越好。

Gardner算法的成立条件大多是容易满足的，只有假设相位偏差恒定这一条不容易满足[7]。如果有载波偏差存在，相响，在载波偏差Δf与符号周期T之间满足等近于0，Δτ趋近于无穷大，TED模块的精确度也就趋近于无穷差。现在证明这一点：

设有载波偏差的信号y（t）=x（t）·exp（j2πΔft），x（t）此时为没有载波偏差的理想信号，有

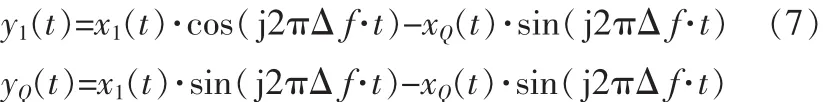
假设可以对x（t）进行直接采样，令对x（t）进行直接采样得到的Gardner算法表达式是Ur（τ）ideat。y（t）对采样得到的Gardner算法表达式是Ur（τ）offset，有：

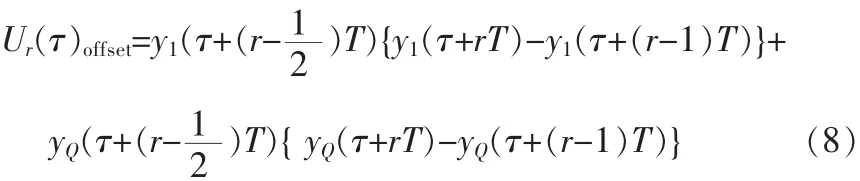
把式（9）代入式（10）中，合并同类项后得到：

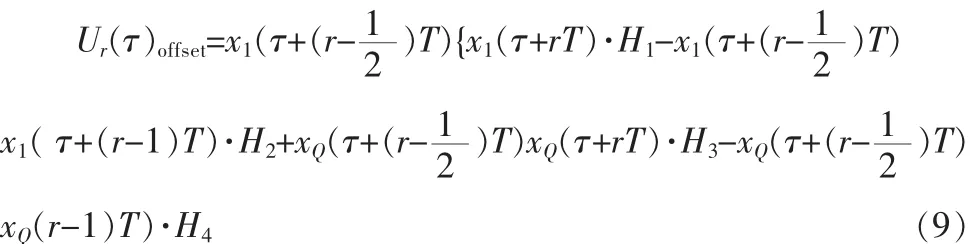
其中H1、H2、H3和H4分别代表一个关于Δf和τ的三角函数：

运用三角公式，有：

对于H3和H4情况做同样的推导，可得：

将式（14）代入式（11）可以得到：

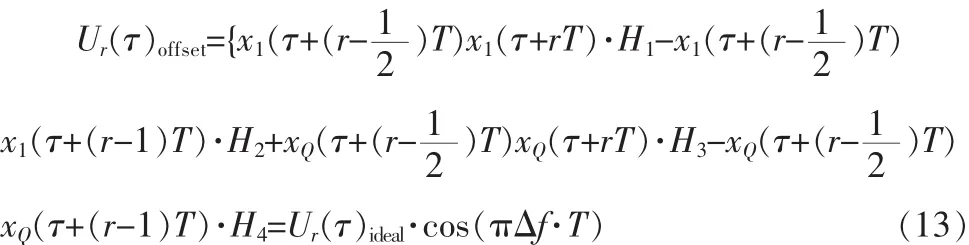
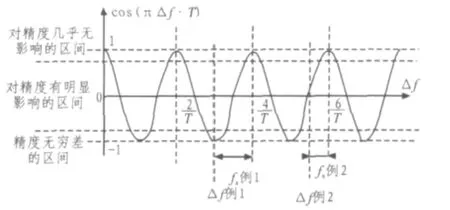
图4 Δf对精度的周期影响Fig.4Δf’s periodical impact on the accuracy

对于解决这个问题，只需对有载波偏差的信号做一个跨度为fa的频谱搬移，使得{fa+Δf}的值处于对TED精度几乎没有影响的区间上。fa的值可以在不求得Δf的情况下得到。因为cos（πΔf·T）的值可得，所以可以得的最大的整数，如图4所示。cos（πΔ·fT）的值是由式（14）得到的。块的工作原理并非一劳永逸地计算出一个不变τ的值，而是始终不断地计算{E（Ur（τ））}的值来跟踪τ值的变化[8]，所以TED会反复计算出τ=0附近的多个{E（Ur（τ））}的值，只需要把这些值存储下在TED内，并不断更新，就能计算出于在信号平均功率、采样周期、脉冲形状既定的情况据式（14），cos（πΔf·T）也可以得出，从而得出fa：

得到fa后只需用y（τ+rT）·exp（j2πfa·rT），（r∈N）和y（τ+可得到几乎不受Δf影响的接近{E（Ur（τ）ideal）}的{E（Ur（τ））}值，从而在有载波偏差的情况下得到高精度的τ。

2 仿真结果

原算法和改进后的算法使用matlab7.0做了对比仿真，图5中的左右两个图都是由仿真得到。图5中纵轴是把接收信号采样点的平均功率归一化为1后，Gardner表达式的值，横轴是用2 000个离散的时间代表一个周期τ内的连续时间。由结果可以清晰看到，改进后的算法可以对每一个Δf都能给出在τ=0附近有较大斜率的曲线，也就是说：对仿真中使用的每一个Δf的值，改进后的算法都不受影响，能给出接近理想的精度。仿真使用的是QPSK信号，符号函数使用的是滚降系数是0.5的升余弦函数，AWGN信道。图5是输入信号信噪比为30 dB的仿真结果。

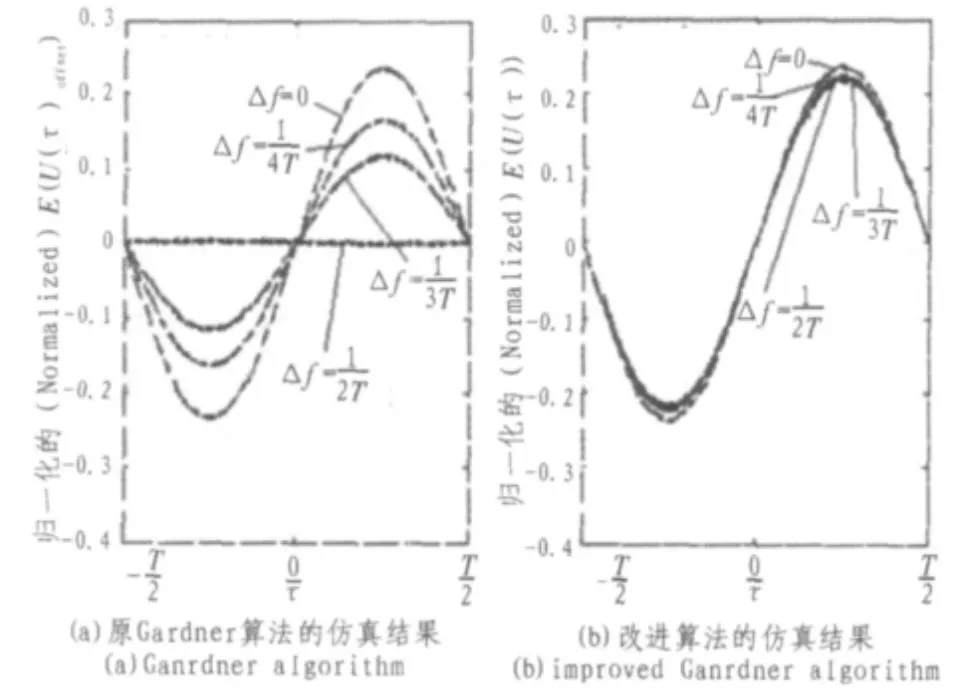
图5 对比仿真结果Fig.5Simulation results in contrast

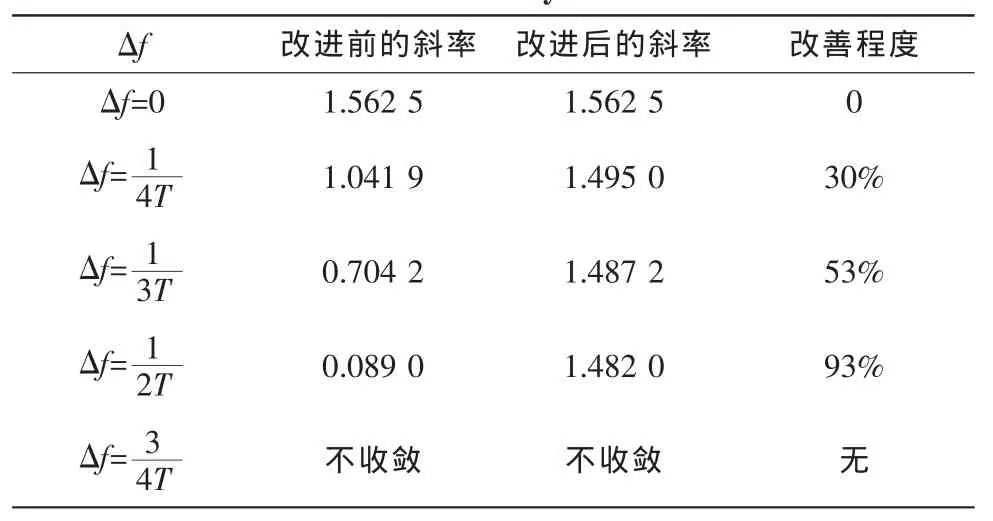
表1 改善前后精确度对比Tab.1Accuracy contrast

3 结论

本文提出了一种对数字通信中的TED模块Gardner算法的改进，并给出了改进算法的数学证明和仿真结果。改进后的算法增强了Gardner算法可能对抗波偏差的性能，同时继承了Gardner算法的实现简单、硬件消耗较小、精确度高、对相位偏差不敏感的特点。同Gardner算法一样，改进后的算法适用于BPSK、QPSK的带限信号和AWGN信道，对QAM信号和严重的多径信道表现欠佳。

[1]GARDNER F M.A BPSK/QPSK timing error detector for sampled receiver[J].IEEE Trans.On Comm，1986，34（5）:423-429.

[2]PELET E R，SALT J E.On economical timing-error detectors for QAM receivers[J].IET Communications，2007，1（4）:618-622.

[3]LOU Huang.A new lock detector for Gardner’s timing recoverymethod[J].IEEETransactionsonConsumer Electronics，2008，54（2）:349-352.

[4]GAPPMAIR W.Self-noise performance of zero-crossing and Gardnersynchronisersappliedtoone/two-dimensional modulation schemes[J].Electronics Letters，2004，40（16）:1010-1011.

[5]GAPPMAIR W，Cioni S，Corazza G E，et al.Symbol-timing recovery with modified Gardner detectors[C]//International Symposium on Wireless Communication Systems，Siena:[s.n.]，2005：831-834.

[6]MAHLOUJI M，DANESFAHANI R.An investigation into timing synchronization of pi4-DQPSK signals using Gardner symbol timing error detectionalgorithmandpolyphase filterbanks[C]//Information and Communication Technology，Damascus:[s.n.]，2006：2274-2278.

[7]LOU Huang.Timing recovery methods for VSB receivers[J].IEEE Transactions on Consumer Electronics，2007，53（2）:310-312.

[8]GONG Feng-kui，GE Jian-hua，QIAN Feng.Symbol timing recovery algorithm with near timing-jitter free for ATSC DTV receivers[J].IEEE Transactions on Consumer Electronics，2007，53（2）:313-318.