基于GIS的降水多元回归模型在黑河干流山区的应用

梁友嘉，徐中民

(中国科学院寒区旱区环境与工程研究所 内陆河流域生态水文重点实验室，甘肃 兰州 730000)

环境研究、管理和规划是当今科学研究的一个重要领域，如农业和森林管理、水文-生态建模、环境影响评估等，在这些研究中通常要求具有空间连续的降水数据[1-2]。然而，降水量一般只能通过非常有限的一些站点进行观测，尤其在山区，受自然条件等因素制约，站点选址和建设非常困难。数据缺乏或数据精度的问题使得精确模拟和预测降水成为一项极具挑战性的工作[3]，近年来地理信息系统(GIS)的快速发展，为降水量建模的深入研究提供了更多的机会。

长期以来，国内外已有很多如何将有限站点上同一时间内的实测值外推到一个区域的研究，并总结出多种方法[4]。概括起来主要包括统计模型法、空间插值法和综合方法3种类型。统计模型法是根据实测站点信息，建立降水量与地理位置、地形及气象等因子间的关系，分析降水量空间变化规律；空间插值法常用的有反距离加权插值法、全局多项式插值法、局部多项式插值法、径向基函数插值法、克里金插值等方法；综合方法是将统计模型同空间插值相结合的方法。但是，各种方法都有特定的假设、适用范围和优缺点，很难说哪个是最优空间内插方法，只有特定条件下的最优。然而，上述传统插值方法仅考虑了样本点之间的空间关系，未能考虑其他重要地形参数。这些插值方法难以给研究者提供一个满意的降水量模拟精度，尤其是在地形复杂的山区[5-7]。近年兴起的地统计方法对空间变异现象有更强的表现力，使得研究者有可能对空间不确定性问题进行精确模拟，地统计方法已经成为气候学研究乃至整个地学研究中的一个重要工具[8-10]。

近年来，地理和地形因素已逐渐被纳入到降水建模中[11-14]，一些学者尝试引入地形因素，如在地统计方法中引入高程[15]，还有一些模型加入了空间位置因子。已有一些研究[16-20]分析了降水空间分布与地形之间的关系。基于降水量-高程回归的独立坡度模型(PRISM，parameter-elevation regression on independent slopes model)在地形雨分析中已经融合了气象和统计学思想，回归模型中普遍引入了权重函数[21-23]。很多研究[24-25]表明，利用更高空间分辨率的数字高程模型(DEM，digital elevation model)可以更好地揭示地形变量在降水量模型中的作用，与GIS、统计学的紧密结合已经日益成为降水量模型发展的趋势。也有研究[26-28]证明，多元回归模型在降水量模拟中效果更好。

本研究以黑河干流山区为研究对象，结合GIS和统计学方法，利用气象数据和DEM构建一种多元非线性回归模型，用以模拟研究区降水量空间分布，主要基于5个因子进行分析：高程、坡度、坡向、经度和纬度。

1 数据与方法

1.1研究区概况 黑河为我国第二大内陆河，发源于南部祁连山区，穿过河西走廊，最终消失于广袤的戈壁和沙漠，是我国典型的内陆河流域(图1)，面积130 000 km2。其中，黑河干流山区流域面积10 009 km2，海拔1 674～4 823 m，出山径流由莺落峡水文站控制(38°48′ N,100°11′ E)。整个山区流域被多年冻土和季节性冻土覆盖。植被覆盖度高，降水较多，固态降水比例较大，冰川覆盖面积59 km2，冰川覆盖度0.59%，冰川储水量13.808×108m3，径流量16.05×108m3，冰川融水补给率为3.4%。

图1 研究区示意图

1.2数据来源 所选21个站点降水数据和DEM(图2)均来源于数字黑河网站，其中，DEM由1∶25万比例尺的地形图建立，格网分辨率为100 m；观测站点海拔介于1 480～3 367 m。本研究采用各站点1971-2000年30年降水资料分析，统计结果表明，85.22%的多年降水均发生在5-9月，因此将这5个月份划分为湿季，其余月份为干季，以便深入分析不同情况下模型的效果。

1.3方法 首先采用统计分析(站点降水量与所处位置经纬度以及高程之间的统计关系)、反距离加权(IDW，inverse distance weight)、全局多项式(GPI，global polynomial interpolation)、局部多项式(LPI，local polynomial interpolation)、径向基函数(RBF，radial basis function)、普通克里金(OK，ordinary kriging)、普通协克里金(OCK，ordinary cokriging)7种插值方法[29-30]，对黑河干流山区降水量进行插值，利用ArcGIS探索性空间数据分析技术(ESDA,exploratory spatial data analysis)对插值效果进行比对，然后选择插值效果最优的方法。经验证发现，在黑河干流山区使用地统计分析中的普通克里金插值效果最好，故本模型基于普通克里金插值法构建。影响降水及其空间分布的因子很多，通常，降水随高程增加而增加，不同坡度和坡向也有很大影响[31]，本研究还考虑了地理位置，作为衡量研究区不同点相对位置的经度和纬度因子被加入到模型中。

图2 研究区数字高程

借助ArcGIS 9.2的强大功能，利用研究区100 m分辨率的DEM为数据源，投影坐标系统为WGS 1984_Transverse_Mercator，在此基础上，通过空间分析生成5个栅格图层：经度、纬度、坡度、坡向、高程。各栅格图层都是基于100 m×100 m格网分辨率，然后导出各栅格图层中每个栅格的属性值，在SPSS 17.0中进行数据预处理；再类似的利用DEM分别生成基于500 m及1 000 m分辨率的5种栅格图。分别利用3种不同分辨率数据进行模型构建，考虑模型的使用范围及数据可获取性，利用研究区内的典型站点(莺落峡、野牛沟和祁连山站)自2001年以来的降水量数据进行模拟精度验证，最终分析不同尺度的变化规律及空间降水特征，具体的技术流程见图3。

图3 技术流程图

研究表明[32]，融合统计方法(多元回归)和空间插值(普通克里格插值)降水量模拟方法是十分有效的。考虑到线性方程不能很好地解释降水量和地形变量之间的关系，尝试采用如下降水多元非线性回归模型进行分析：

P=a+a1X+a2X2+a3X3+a4Y+a5Y2+a6Y3+a7S+ a8S2+a9S3+a10A+a11A2+a12A3+a13H+ a14H2+ a15H3。

(1)

式中,P为降水量(mm)；a为常数项；ax(x=1,2，…，15)为模型中各独立变量的系数项；X、Y分别为经度(°)和纬度(°)；S为坡度(°)；A为坡向；H为高程(m)。考虑3种格网分辨率，具体构建9种模型，模型编码见表1，利用SPSS 17.0进行计算。

2 结果与讨论

2.1模型比较与选择 表2、3、4分别为100、500、1 000 m分辨率下的统计学结果，3种空间尺度下X2、Y2、Y3、H2的系数均为0，即对降水量没有贡献，最终模型中剔除这4项。根据修正的拟合度系数(Adj_R2)和F对比分析表明，100 m分辨率的模型整体效果最好，1 000 m分辨率的模型效果最差，说明随着DEM空间分辨率的提高，模型精度相应增加。同时，还可以发现三者之间差距并不大。而在时间尺度上，全年、干季和湿季的模型精度也各有不同。3种模型中，湿季降水回归模型均最显著，其次是全年降水回归模型，显著性最低的是干季降水模型。这种规律表明，通过干湿季划分可以更好地解耦多年降水量，使得不同季节不同时段的降水量可以得以精确模拟，为基于降水的深入研究提供高精度的数据支撑。黑河流域研究中常用的年降水量计算公式(Adj_R2=0.807)：

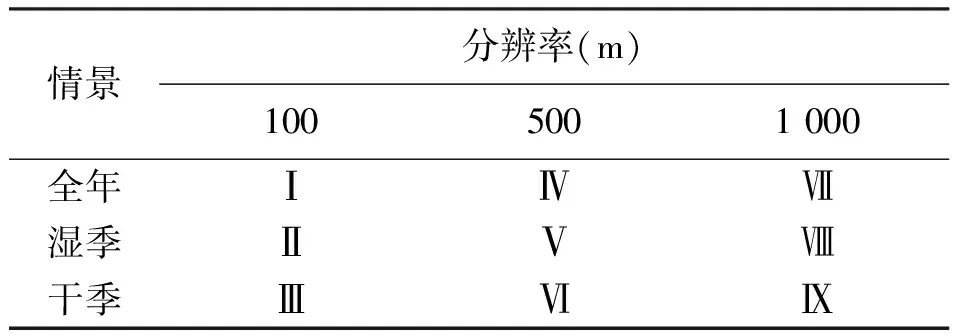
表1 模型编码

P=13 579.361-4.571X-1.218Y-0.055S+0.003S2-0.009A+0.003H。

(2)

2.2精度验证 利用研究区内莺落峡、野牛沟和祁连山3个水文站自2001年以来的降水量实测数据进行验证，模拟结果选用效果最好的基于100 m分辨率构建的模型得出，通过预测值与模拟值相对误差验证模型的模拟效果(图4)。每个站点的数据均处理为全年、湿季和干季3种，与构建的模型结果进行对比。结果表明全年降水模型中精度大小顺序是野牛沟>莺落峡>祁连山；湿季降水模型中为莺落峡>野牛沟>祁连山；而干季降水模型中为莺落峡>祁连山>野牛沟。模型Ⅰ-Ⅸ的最大相对误差7.01%，为祁连山站全年降水模型；最小相对误差1.97%，为莺落峡站湿季降水模型。整体看，每种空间尺度下的模型均具有较高的精度，对验证站点的年降水量模拟精度加权求和，计算的式(2)的精度为74.5%。这在空间化的年降水量分析中，有一定实践意义。

2.3空间降水特征分析 3种空间分辨率下，黑河干流山区近30年来年均降水量为371～231 mm，区域分布不均匀，由西北向东南年降水量逐渐增加，可以沿野牛沟和祁连山站大致画一条自西北-东南向的45°线，线上侧降水明显减少(图5-Ⅰ、Ⅳ、Ⅶ)。

3种空间分辨率下的湿季(5-9月)降水量为337～200 mm，自西北向东南逐渐增加(图5-Ⅱ、Ⅴ、Ⅷ)，同样有类似于年均降水量分界线的特点，但沿原45°方向呈一条带状存在，地带性的差异也得到了较好的反映，较年均降水分布而言，湿季降水45°带略微上移。5-9月降水量占年降水量65%以上，径流量占年径流量的80%左右，侵蚀量占年侵蚀量的83.8%[33]。5-9月正是黑河中下游植被和农作物的生长季，所以认识5-9月的降水量分布特点对该区的植被生长和生态环境评价具有重要意义，也对中下游地区的生态环境建设具有重要作用。

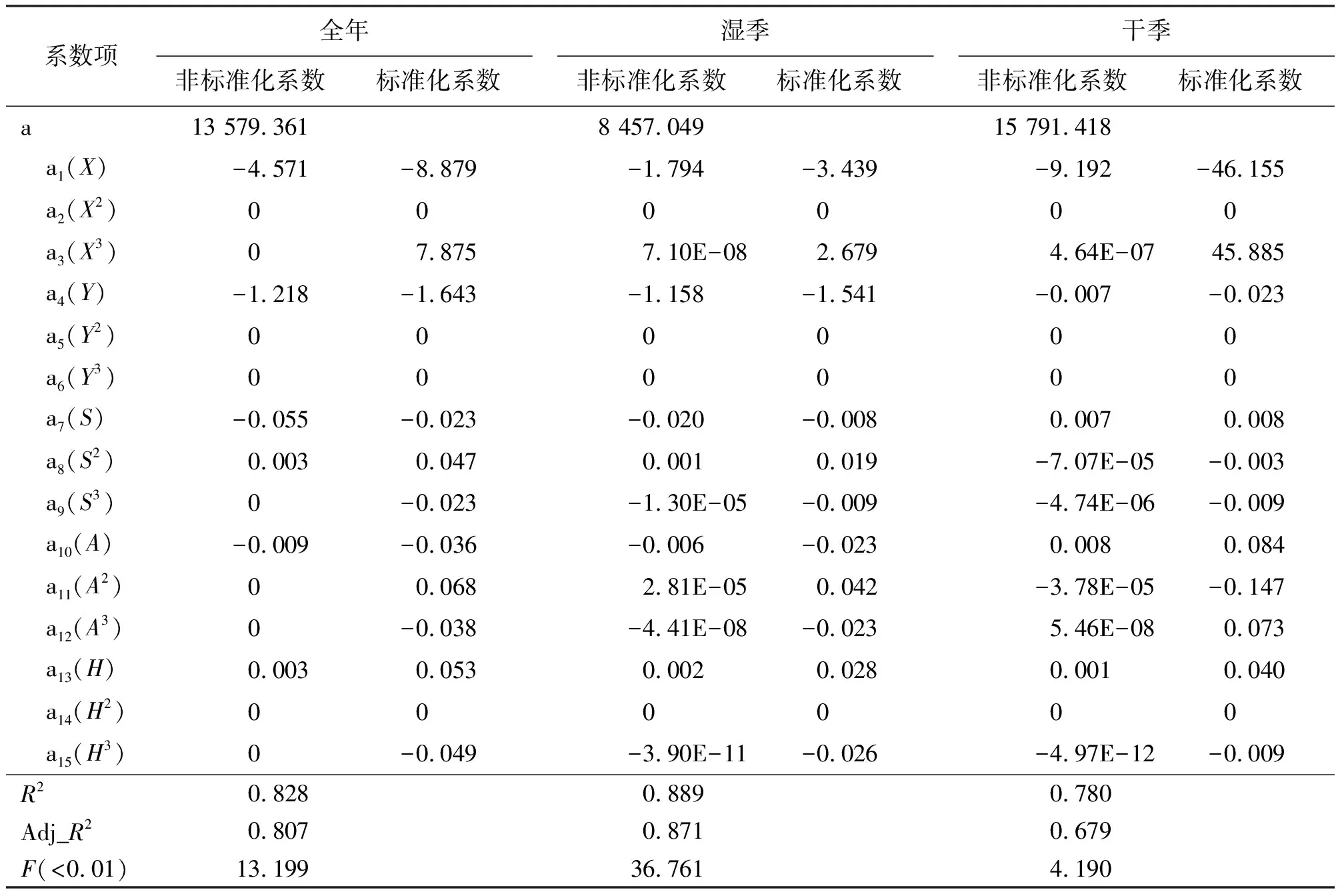
表2 基于100 m分辨率的多元回归模型系数

表3 基于500 m分辨率的多元回归模型系数

表4 基于1 000 m分辨率的多元回归模型系数

图4 模型精度验证

图5 不同研究尺度下的空间降水分布

3种空间分辨率下干季降水量范围为64～12 mm，雨量明显减少，雨量空间分布特征也明显不同于全年降水和湿季降水，西北和东南降水较多，研究区中段降水很少，且占整个研究区面积50%左右，低降水量的空间分布特征明显不同于前两种情况，说明在干季情况下，空间插值方法及模型空间表现力的精度都有一定程度下降(图5-Ⅲ、Ⅵ、Ⅸ)。

另外，对比图2的DEM可以发现，图5中高海拔地区降水明显高于其他地区，说明一定范围内，降水量随海拔升高而增加；同时，受地形和热力条件影响，山区降水明显多于周围地方。从全区域来看，多年平均降水分布与海拔高度之间的显著相关程度最高。

3 结论

本研究开发的基于100 m分辨率DEM的多元回归模型可以解释黑河干流山区74.5%年降水空间变异，不同空间尺度下，对湿季的降水量解释效果均要好于全年和干季两种情景。分析发现黑河干流山区年降水量区域分布有如下主要特点：区域分布不均匀，由西北向东南年降水量逐渐增加，由西北部不足200 mm增加至东南部700 mm左右；基于100 m分辨率的多年降水量分界线呈东北-西南走向；基于500 m分辨率的多年降水量分界呈带状分布，并有一定程度的上移。

多元回归模型在统计学中已经具有一定普遍性，可以解释大部分山区降水的空间变异情况，本研究利用DEM和一些有限站点的降水数据进行建模，该方法具有很强的移植性，可以在其他山区开发类似的模型，并利用GIS技术实现结果的空间化，以便进一步利用其结果进行相关的深入研究，如气候研究等。考虑到当地盛行风的因素，尤其是风向和强度的影响，这也应当是降水模型中的重要变量，本研究因数据受限暂未加入相应的分析，今后在建模中加入空间化的风速变量有可能进一步提高模型精度。

[1]孔云峰,仝文伟.降水量地面观测数据空间探索与插值方法探讨[J].地理研究,2008,27(5):1097-1108.

[2]Alijani B,Ghohroudi M,Arabi N.Developing a climate model for Iran using GIS[J].Theoretical and Applied Climatology,2008，921：103-112.

[3]Gemmer M,Becker S,Jiang T.Observed monthly precipitation trends in China 1951-2002[J].Theoretical and Applied Climatology，2004，77:39-45.

[4]邓晓斌.基于ArcGIS两种空间插值方法的比较[J].地理空间信息,2008,6(6):85-87.

[5]Sharples J,Hutchinson M F,Jellett D R.On the horizontal scale of elevation dependence of Australian monthly precipitation[J].Journal of Applied Meteorology,2005,44(12):1850-1865.

[6]马轩龙,李春娥,陈全功.基于GIS的气象要素空间插值方法研究[J].草业科学,2008,25(11):13-19.

[7]Shaw M R,Zavaleta E S,Chiariello N R,etal.Grassland responses to global environmental changes suppressed by elevated CO2[J].Science,2002,298:1987-1990.

[8]朱求安,张万昌.流域水文模型中面雨量的空间插值[J].水土保持研究,2005,13(4):11-14.

[9]Tsanis I K,Gad M A.A GIS precipitation method for analysis of storm Kinematics[J].Environmental Modeling and Software,2001,16:273-281.

[10]Marquínez J,Lastra J,García P.Estimation models for precipitation in mountainous regions:The use of GIS and multivariate analysis[J].Journal of Hydrology,2003,270(1):1-11.

[11]Goodale C L,Aber J D,Ollinger S V.Mapping monthly precipitation,temperature,and solar radiation for Ireland with polynomial regression and a digital elevation model[J].Climate Research,1998,10:35-49.

[12]Hutchinson M F.Stochastic space-time weather models from ground-based data[J].Agricultural and Forest Meteorology,1995,73:237-264.

[13]秦建成.ArcGIS支持下样本稀疏山区空间插值模拟探讨[J].长江流域资源与环境,2009,18(5):489-494.

[14]孙鹏森,刘世荣,李崇巍.基于地形和主风向效应模拟山区降水空间分布[J].生态学报,2004,24(9):1910-1915.

[15]朱会义,贾绍凤.降水信息空间插值的不确定性分析[J].地理科学进展,2004,23(2):34-41.

[16]伍光和,江存远.甘肃省综合自然区划[M].兰州:甘肃学科技术出版社,1998.

[17]何红艳,郭志华,肖文发.降水空间插值技术的研究进展[J].生态学杂志,2005,24(10):87-91.

[18]徐超,吴大千,张治国.山东省多年气象要素空间插值方法比较研究[J].山东大学学报(理学版),2008,43(3):1-5.

[19]赵传燕,冯兆东,南忠仁.陇西祖厉河流域降水插值方法的对比分析[J].高原气象,2008,27(1):208-214.

[20]Goovaerts P.Geostatical approaches for incorporating elevation into the spatial interpolation of rainfall[J].Journal of Hydrology,2000(228):113-129.

[21]Daly C,Neilson R P,Phillips D L.A statistical topographic model for mapping climatological precipitation over mountainous terrain[J].Journal of Applied Meteorology,1994,33:140-158.

[22]Vicente Serrano S M,Saz Sanechez M A,Cuafrat J M.Comparative analysis of interpolation methods in the middle ebro valley (Spain):Application to annual precipitation and temperature[J].Climate Researeh,2003,24(2):161-180.

[23]李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3):21-26.

[24]Brown D P,Comrie A C.Spatial modeling of winter temperature and precipitation in Arizona and New Mexico,USA[J].Climate Research,2002,22:115-128.

[25]黄杏元,马劲松,汤勤.地理信息系统概论[M].北京:高等教育出版社,2005,93-97.

[26]Guan H,Wilson J L,Makhnin O.Geostatistical mapping of mountain precipitation incorporating auto searched effects of terrain and climatic characteristics[J].Journal of Hydrometeorology,2005,6:1018-1031.

[27]封志明,杨艳昭,丁晓强，等.气象要素空间插值方法优化[J].地理研究,2004,23(3):357-364.

[28]林忠辉,莫兴国,李宏轩，等.中国陆地区域气象要素的空间插值[J].地理学报,2002,57(1):547-561.

[29]赵传燕.甘肃省祖厉河流域潜在生态条件的GIS辅助模拟研究[D].兰州：兰州大学,2003.

[30]冯兆东,刘勇,陈发虎.黄土高原的流域水文和景观生态研究与设计:地理信息系统辅助的过程模拟[J].中国沙漠,2000,20(2):271-287.

[31]Loyd C D.Assessing the effect of integrating elevation data into the estimation of monthly precipitation in great Britain[J].Journal of Hydrology,2005(308):128-150.

[32]Ninyerola M,Pons X,Roure J M.Monthly precipitation mapping of the Iberian Peninsula using spatial interpolation tools implemented in a Geographic Information System[J].Theoretical and Applied Climatology,2007,89:195-209.

[33]魏智,金会军,蓝永超，等.基于Kriging插值的黑河分水后中游地下水资源变化[J].干旱区地理,2009,32(2):196-203.