智能运输调度系统求解机制研究与实现*
2011-03-13任中明蔡延光
任中明 蔡延光
(广东工业大学 自动化学院)
1 引言
减少运输费用是降低物流成本的重要手段[1],而运输费效比又与调度方案的优劣密切相关。运输调度是物流企业中的核心作业,对于降低物流成本及提高服务水平具有关键作用。合理正确的调度可以有效减少车辆的空驶率,实现合理路径运输并有效减少运输成本。同时,在现代物流管理中,运输调度的工作量大、技术性强,要实现调度过程优化具有相当难度。因此,对运输调度的深入研究具有重要的社会效益和经济效益。
概括来说,运输调度问题(Vehicle Routing and Scheduling Problems, VRP&VSP或VRSP) 是指能够在满足一定的约束条件(如车辆、时间窗、运输数量要求及运输能力限制等)下,给出适当的行车路线和任务分配方案,达到一定的目标(如综合费用极少、路程最短、时间最少、使用车辆数尽量少等)。
VRSP模型具有类型多、约束条件多、变量多、结构复杂及求解工作量大等特点。VRSP已被证明属于NP-完全问题,具有扩展特征的VRSP也属于NP-完全问题[2]。针对VRSP的求解问题,国内外学者已提出的算法大体上分为三类:精确算法、近似算法和启发式(智能)算法。经典的精确算法有分支定界法、K树算法、动态规划法等。这类算法能够求得问题的最优解,并且具有求解速度快的优点,但是缺点在于:往往只针对小规模的VRP问题有效,而且只能求解一些确定性、弱约束的理想化问题,难以用来求解NP-完全问题。近似算法则主要包括先路线后聚集、先聚集后路线、松弛法以及改进与交换法等算法。
采用近似算法能够显著缩小可行解的解空间并降低求解复杂度,但是采用近似算法来求解VRSP也只是在某种程度上的改善求解质量,并不能处理实际复杂的多目标优化问题。启发式(智能)算法不以找到精确解为目标,而是在复杂问题中以可接受的代价给出问题的次优解,代表算法有构造算法、不完全优化算法、节约算法、遗传算法、模拟退火算法、蚁群算法、禁忌搜索算法、粒子群算法等。启发式(智能)算法的应用,可以在很大程度上缓解由于模型组合的复杂性及模型的不完备性而带来的求解难度,有效地提升了对VRSP的求解效率,并使求解结果更趋于实用。然而,针对某一类VRSP问题采用某种(或改良的)智能算法来求解也许是可行及高效的,但是现实中的VRSP模型却是受动态时变、多条件约束及环境不确定等因素紧密制约的。单一算法既不能适应实际的复杂环境,也不能在应对大多数的多目标优化运输调度问题时给出满意的可行方案。
基于以上分析可见,试图用一种智能算法或是改良的智能算法去求解所有的VRSP是不可能的,也无法满足对复杂多变环境的实际需求,采用此种方法开发出的系统通用性也较差,求解问题对象也受到很大的局限性。因此,开发一套简洁、高效、知识化、实用性强并且具有一定智能处理能力的求解VRSP模型的软件具有重要实际意义。应用智能运输调度系统可提高运输调度工作效率和调度水平,降低物流运输成本。针对VRSP问题,本文通过对典型运输调度模型的分析,并结合模型类参数结构[3],提出一种基于智能框架的求解平台的构建方法和运行机制,并重点研究了VRSP模型类自动识别问题。
2 VRSP模型分析
自1959年VRP问题被Dantzig和Ramser首次提出以来,它的数学模型就随着研究的深入而不断得到扩充完善,出现了各种针对不同问题,包含不同约束内容及变量条件的数学模型[4~5],归结起来有两种风格:基于车流的VRSP模型;基于物流的VRSP模型。本文采用基于物流的VRP模型,可表示为:

其中,式(1.1)为目标函数,规定优化目标为所有车辆行驶的路径最短;式(1.2)~(1.4)是车辆装载能力限制,用来确保车辆的载货量始终不超过其装载容量;式(1.5)表示道路约束,保证车辆行驶的路径长度不超过其最大里程;式(1.6)~(1.8)表示任务约束,式(1.6)用来确保每个客户都被访问到,且每条路径上的客户数不超过总客户数;式(1.7)表示每条路径的客户的组成;式(1.8)限制每个客户只能由一台车辆服务;式(1.9)表示车辆k是否参加了配送,参加为1,否则为0。
从上述VRP数学模型可以看出VRP模型结构复杂、规模庞大,同时具有参数众多及数据关系复杂的特点。基于VRP的涵义,并分析公式模型可以看出VRSP模型事实上是由目标参数、约束条件(多种约束的组合,包括供需点、车辆、时间、路径等)以及变量三个部分组成。在结构化处理VRSP模型的需求下,可以将VRSP模型的参数[3]分为标准模型参数和扩展模型参数两大类。其中,标准模型包括:1-车队结构参数,2-供应结构参数,3-需求结构参数,4-网络结构参数,5-作业类型参数;扩展模型包括:6-约束条件参数,7-函数及数字特征参数,8-目标函数参数。同时,鉴于计算机对自然语言理解的局限性,并为了方便计算机对模型求解目标及约束条件的理解处理,对模型类的参数进行数字编码。
以车队结构参数编码含义为例说明(数字为编码,-表示分割符,后面内容为编码含义):则 1-车队结构参数下的各参数编码方式如下:
11-车队数量:111-一个;112-一个以上;113-待定。
12-车队位置:121-固定;122-待定。
13-每个车队拥有的车辆数:131-一辆;132-一辆以上;133-待定。
14-车辆重量:141-所有车辆的载重量相等;142-所有车辆的载重量不完全相等。
15-车辆类型:151-普通车辆;152-专用车辆;153-普通和专用车辆混合车队。
采用同样的编码方式可以获得所有已确定参数类型的模型参数编码,限于文章篇幅,读者可参阅参考文献[3]中第2节模型分类与表示的相关内容。
3 系统运行机制设计
VRSP模型类的表示方式为系统提供了运行支持,它负责为VRSP问题信息的人机交互、模型辨识、模型处理、知识化模型的生成、模型求解的整个处理过程提供模型表示支持。系统的详细设计从数据组织、模型库构造、算法库管理、规则库构造、经验库构造、学习机制及解题机制几个方面依次入手。而系统在模块上大体则可划分为:输入输出模块、知识库管理模块、学习子系统以及主处理程序模块。同时,鉴于智能算法的在VRSP问题上的求解优势,依托该类算法特征进行系统运行机制的设计。采用此方法构建的求解系统,能够综合利用智能算法求解大规模VRSP模型的优势和智能决策系统的计算经验来简化VRSP的求解过程以及降低计算复杂程度。系统运行机制如图1所示.
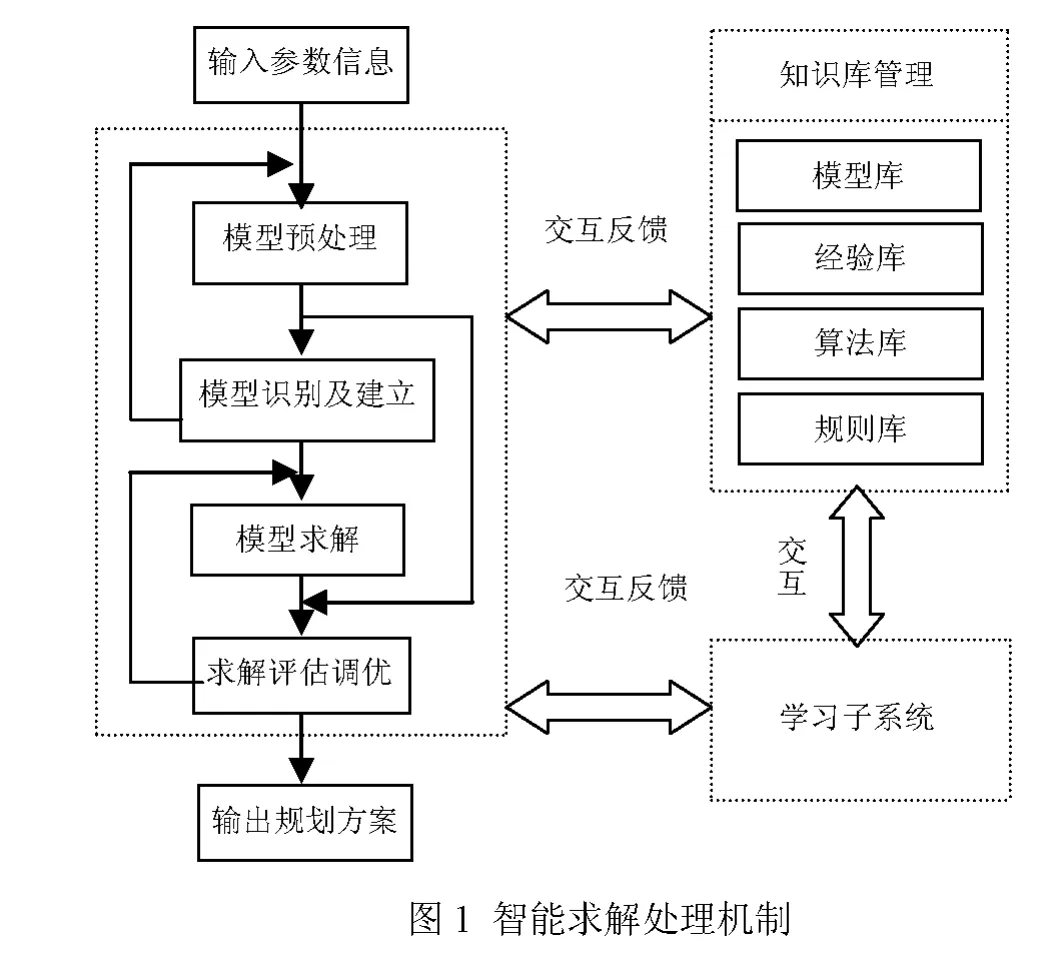
基于图1所示的求解处理机制,系统的各个模块的组成及功能如下:输入输出模块包括输入参数信息和输出规划方案。知识库管理模块包括模型库、算法库、经验库及规则库管理及使用,模型库用于存放已有过求解记录的典型模型类,算法库用来存放求解模型所用到的算法文件路径或者算法代码,同时提供算法的输入输出函数接口,规则库是用于存储从问题基本信息到问题模型表示的转换规则,经验库则存储经验模型的求解算法经验。主处理程序模块则包括模型预处理、模型识别及建立、模型求解、求解评估调优几个阶段,对于其处理步骤以下做重点阐述。
3.1 模型预处理
由调度人员完成输入VRSP模型的各种变量及参数信息。首先,由系统对输入信息进行初次分类、整理、分析,筛选出无法为系统识别处理的条件,以备对规划结果需进行调优时作为参考条件用。然后,通过对输入参数信息的分析、提取及再次整理,生成对应的网络拓扑结构。在此过程中,针对规模较大的网络拓扑时,可以考虑采用近似算法来缩小可行解的搜索空间以降低求解复杂程度,如采用先聚集后路线的算法将部分集中的点作为一个点来处理,在完成总体的求解后,再将此点分解为一个子拓扑网络进行迭代求解。最后,根据筛选后的参数信息,结合VRSP模型的类参数编码规则,生成对应参数的编码。
3.2 模型识别及建立
根据之前生成的对应参数编码,组合模型的编码表示方式。依据VRSP模型的定义[3],模型之间存在多种关系,如父子关系、相似关系、运算关系、等价关系、派生子类等。这些关系的存在不仅极大的扩展了模型类的类型,同时也为模型的求解提供了极大的有利条件。对模型之间的关系的探究,对降低模型的复杂程度、缩减可行解的状态空间数量以及减少求解的运算量都能起到积极作用。
(1)父类与子类
模型的父子关系可以简单描述为集合中的包含关系。例如,如果VRSP模型中车队数量取值为待定,其实数量就包含了一个及一个以上,此时假定其他的条件都相同,并且已存在对单车队的求解,如果再去求解待定车队的问题,则对单车队的求解经验完全可作为经验解调用。此关系对其它参数(如每个车队拥有的车辆数、车辆类型及供应点数量等)同样适用。
(2)相似类
由于VRSP模型类的不完备性,使得获取的新模型的模型结构不可预料以及新模型的经验算法可能不存在。此时,通过引入逆反算子、松弛算子等手段来获取相似类,进而通过与相似类的类比、自动学习获取求解经验,导出对问题求解的新算法。
(3)类的运算
VRSP模型类的参数标准化也为模型类的运算提供了支持。模型的运算包括交、并、补等运算方式。其运算关系等价于集合的交、并、补运算。特殊之处在于,模型类的运算在于为模型库的扩展找到一条切实有效的途径,并可以通过运算分解或组合要求解的模型,充分利用已有求解经验来达到求解实际问题的目的。
(4)等价类
在VRSP模型中引入等价类是为了实现在求解概念意义上相同的模型的算法的互用。等价类在很大程度上与输入的参数有关,也是多样的。例如,假定VRSP模型中的其他条件相同,则车辆数为1且车辆载重量相等的任意类与车辆数为1且车辆载重量不全相等的任意类事实上是等价的,即为等价类。
(5)派生子类
通过一个多项式复杂度的单值或多值算子使模型类B变换得到的模型类为模型类A的子类,则说明两个模型类具有派生子类的关系。
以上的模型关系可存放于规则库中供模型求解过程中的各阶段使用。当然,模型的识别还要求在数据库中已经存在相应的典型模型。通过对各种模型类的关系分析利用,可以实现在多数情况下对新模型的识别,也能够充分利用模型结构相似性、数据相似性和已有的计算经验来简化求解过程以及降低计算复杂程度。
3.3 模型求解
模型关系的确定有利于模型的简化及运算,因此要充分利用模型之间的各种关系来进行模型求解。例如,假设模型类A为模型类B的父类,适合A的求解算法不存在而适合B的求解算法存在,则优先采用B的求解算法进行求解。同样,相似关系、等价类及派生关系的确定,也可以使模型求解时充分利用已有的典型模型类的求解经验,简化模型类求解方式,降低求解复杂度。模型求解的主要步骤如下:
(1) 筛选模型库和经验库,查找是否存在相同的模型类,如果存在则直接调用已存储模型类的处理经验,在参数相同的情况下可以直接调用其结论;如果不存在,转入步骤(2)。
(2) 调用规则库中存储的模型类关系规则,根据规则依次核对新模型类与已存储典型模型类之间是否存在父子关系、相似关系、运算关系、等价关系或派生子类。如果相应的关系存在,则依据规则调用已存储典型模型的处理算法(包括对算法的再处理)求解;如果不存在,转入步骤 (3) 。
(3) 结合模型库、经验库及规则库,针对新模型问题的特点进行分析,生成新的组合模型类,然后用推理机构依据控制策略集中的控制策略调整任务分配方案,选择比较适合的算法,求解此调度问题。
在上述步骤中,如果已有的算法不能够满足当前模型类的求解,则需考虑采用算法的自动生成机制和局部调优机制进行算法的重构。但算法自动重构的实现也面临着相当多的挑战,需要在实践中不断深入研究和完善,并最终达到实用化目的。
3.4 求解评估调优
首先,在对模型类进行求解之前,要依据VRSP模型的输入信息和模型的约束参数,确定要优化的目标,并根据要优化的目标和采用的智能算法采取对应的评价手段及参考指标。其次,采用人机协同寻优的方式(人机协同寻优可以尽量避免系统在运行中因陷入循环而无法获取最终结果,或者因陷入局部最优而得出不可接受的解)评价所获得规划方案是否合理,并在各种方案之间进行分析比较以获取最可行的规划方案;然后,如果获得优化方案不能满足优化目标,则采用新的方式组合模型类,制定评价手段及参考指标并求解,直到取得满意的可行方案。最后,如果获得的优化方案满足优化目标,则输出经优化后的调度方案,并且对相应的经验库、模型库进行更新,同时存储此典型模型类的求解案例。
4 系统的实现
作者采用Delphi7.0编程工具,并在SQL Server 2000数据库环境下,在Windows XP 操作系统上编程实现的智能运输调度求解系统的原型系统,初步实现了部分功能及界面。该系统由Delphi7.0实现流程控制与人机交互界面的显示,由SQL Server 2000数据库系统存储系统的模型类参数库、模型库、求解经验库及规则库。如图2所示为系统在输入参数后的新模型生成界面。

图2 模型生成界面
5 结束语
本文根据复杂运输调度问题的研究状况和发展趋势,简要分析了各种VRSP模型求解算法优缺点,提出了一种基于VRSP模型参数结构化分类的智能求解平台的构建思路和运行机制。在此基础上,尝试用人机结合和集成多种技术的方式来构建开放的、智能化的、可重构的决策支持系统来求解复杂运输调度问题。仿真分析和初步应用的效果令人满意。证明其在处理复杂运输调度问题上具有相当大的潜力。
[1]张燕华,俞健,朱大均.交通经济学[M].上海社会科学院出版社,1998:115-119.
[2]Lenstra J K, Rinnooy Kan A H G.Complexity of vehicle routing and scheduling problems[J].Networks, 1981,11:221-227.
[3]蔡延光,钱积新,孙优贤.智能运输调度系统模型库构造与管理[J].系统工程理论与实践,2000(9):83-90.
[4]魏明,蔡延光.一种基于混沌领域搜索的自适应混沌遗传算法[J].计算机应用研究, 2009,26(2):464-465.
[5]蔡延光,宋康,张敏捷,武鑫.自适应多目标混合差分进化算法在联盟运输调度中的应用[J].计算机应用, 2010,30(11):2887-2890.
[6]郎茂祥.装卸混合车辆路径问题的模拟退火算法研究 [J].系统工程学报,2005,20(5): 485-491.
