表面电磁波与表面等离子波

黄志洵，姜荣

(中国传媒大学信息工程学院，北京 100024)

1 引言

表面电磁波简称表面波(surface waves，SW)，是一种沿两媒质之间界面传播的波。表面等离子波(surface plasma waves，SPW)则发生于金属与电介质之间界面，故SPW是SW的一种。在导波理论中，一根表面裸露的金属圆柱导线，可以工作在分米波、厘米波波段，作为单线表面波波导(Single Wire Surface Waveguide)。1899 年 A.Sommerfeld 指出［1］，如导线的电导率为有限值(σ≠∞，这与实际相符)，则会有TM波型沿导线表面传播。表面波的相速小于光速，在靠近导体表面处携带有其能量的绝大部分。由于Sommerfeld指出的波较弱，也由于20世纪初的很长一段时间内尚不能生产分米波、厘米波的源，Sommerfeld的论断直到几十年后才得到证实。Sommerfeld波存在的条件是电导率σ≠∞，亦即电阻率ρ≠0。因而，ρ＞0表示导线电阻提供了对波的相速的迟滞，从而获得了慢波状态。另外，1909年Sommerfeld用Maxwell方程处理两个媒质分界面上的表面波传播问题(Ann.Phys.，Vol.28，1909，665)，是非辐射型(non radiative)表面电磁波。

1907 年，F.Harms［2］研究了当单根导线表面涂敷有电介质层时的波传播问题。介质层的存在同样满足了Sommerfeld波所要求的边界条件，因而表面波的存在可以不依赖于导线的有限导电率。就是说，即使是理想导体(σ=∞)，波也能传播。1910年，D.Hondros和 P.Debye［3］也论述了这个问题。不过，完整的工作和实验是1950年由G.Goubau完成的［4］，故称为 Goubau Wire。

表面等离子体光子学(surface plasmonics，SP)是一门新兴学科，它的另一名称是表面等离子体激元(surface plasmon polariton，SPP)，是指沿金属/介质界面传播的纵向电磁波(longitudinal EM wave propagating along a metal/dielectric interface)，其电磁场从界面向两边按指数率下降，即消失态(evanescent states)。对SPP或SPW的研究已有百余年历史，例如在金属栅格(metallic gratings)上的激励，早在1902年R.W.Wood即报告过对有关现象的观察(见:Philos.Mag.，Vol.6，1902，396)。又如在 1904年出现了“金属/介质复合材料”的说法，研究了掺有金属微粒的电介质的光学性质。故SPW起因于对金属在微波和光频的介电特性的探讨，借鉴了等离子体理论方法，技术上则创建了金属/介质复合材料系统。1957年，R.Ritchie研究了金属膜中电子束的能量损耗，发现在金属表面区域可能存在等离激子现象，从而首次作出明确的理论表述。1968年，A.Otto［5］提出了在金属薄膜上激发SPW 的实验方法，用玻璃三棱镜作为光的耦合器。1971年 E.Kretschmann［6］作了改进。他们的技术现在仍是广泛使用的研究和实验方法。

2 早期电磁理论中表面波的一般分析

早期研究的表面波是一种沿两媒质之间的界面传播的电磁波，媒质之一通常是空气。界面可以是光滑表面(平面或曲面)，也可以是周期性或不规则结构。表面波比光速慢，在界面处近距离上携带了大部分能量。表面波一般作为被导波而加以研究，但当它在传播过程中遭遇不连续性障碍时，或在专门的表面波天线设计中，它是辐射性的。由于波矢量的一般表示式为假定z为表面波传播方向，x为与界面垂直的法向(指向上方)，如图1;y方向没有波动，可取ky=0，故有

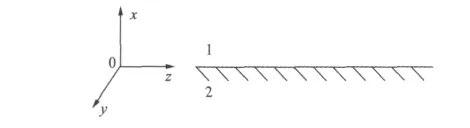
图1 两媒质的界面与坐标选取

取k为空气中的波数，则有

这是表面波遵守的简单方程，kz是沿表面传播的波数，kx是与表面垂直方向上的波数。所有波数均为复数，例如可取

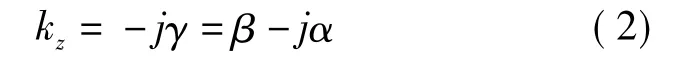
式中 γ是传播常数(γ=α+jβ)。

这组成一种非均匀的波(inhomogeneous wave)，相阵面与表面垂直，幅阵面与表面平行(距表面越远强度越小，是指数衰减)，见图2(a)。

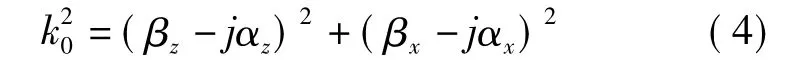
展开后得到两个关系式:

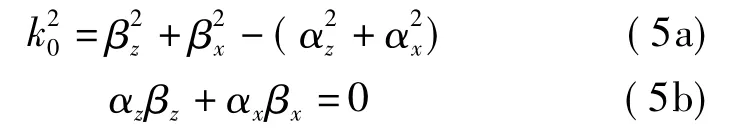
对于向z方向传播的波而言，βz＞0;至于βx，对于从表面浮现的波βx＞0，对于向表面入射的波βx＜0。另外，根据波的z向传播时逐渐减弱，αz＞0;这样，根据(5b)式有αx＜0，表示在x方向振幅指数式增大。在快波(vs＞c)情况下，应把相位常数写成矢量，而βz、βx均是它的分量;故有

图2显示表面波这种非均匀波的慢波与快波的关系，图2(c)是辐射的快波，也叫漏波(leaky wave)，看起来好像由慢波倾斜及倒转而成。实际上，离开表面的倾斜角度是可计算的:

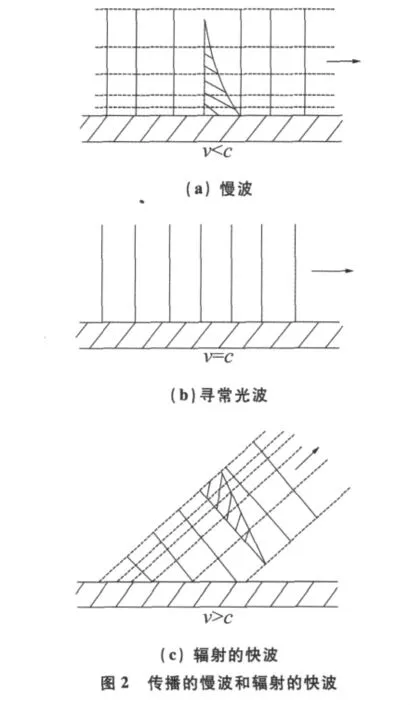
另外，αz与 αx也组合为净衰减常数

以上是早期电磁理论中对表面波的一般分析，讨论中没有具体说明媒质1、2可能是电介质或者金属，给人以空泛之感。但这种分析却讨论了开放式结构中表面波由非辐射性向辐射性过渡的情况，使人认识到表面波导波结构和表面波天线系统的不同。总之，为了获得非辐射型表面波，必须保证波的相速比光速慢。

现以金属管子做成的柱波导(waveguides)进行讨论，传输电磁波的相速为

式中G是波导因子:

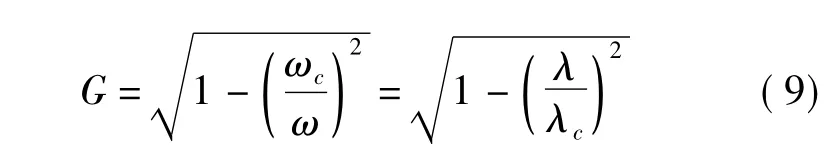
式中ωc、λc分别为波导截止频率和截止波长。如果我们只讨论ω≥ωc的频域，那么从ω=ωc到ω→∞都有G＜1，故vp＞c(快波)。但是，如果ωc是虚数:

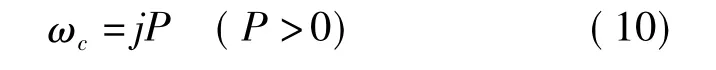
则

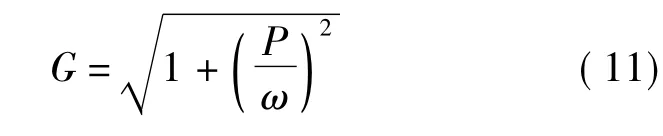
这时总有G＞1，vp＜c(慢波);然而在波导理论中有［7］

h是本征值，也叫截止系数，其定义式为

然而要求ωc为虚数意味着要求h2＜0(获得慢波的必要条件)，亦即要求

从另一角度看，可取

获得慢波的条件又可写作

故要求hx或hy为虚数(或两者均是虚数)，才有可能获得慢波。函数coshxx(或函数coshyy)将是双曲函数。但cosh函数没有零点，sinh函数只有一个零点。然而，一般波导的场分布，场的切向分量有两个零点(理想导体表面电场切向分量为零)。结论是，理想导体的波导系统是不能传输慢波的。但如导体非理想导电(电导率σ≠∞)，并不要求场分布有两个零点，就有可能产生慢波。这个道理可由表面波传输线的早期发展而获得深刻的理解，即前述Sommerfeld线的原理。

3 金属壁圆波导内衬电介质层时的模式分析

为深入了解表面波(SW)与表面等离子波(SPW)这两个理论体系之间的联系，现对一种封闭式电磁结构进行讨论。图3是内衬电介质层时金属壁圆波导的横截面，介质层厚度d=a-b;区域Ⅰ是空气区，区域Ⅱ是电介质区，区域Ⅲ是金属导体区。这种波导内可能有三类模式发生，即表面模(surface modes)、界面模 (interface modes)、内模 (inner modes);其发生条件和特点列于表1［8］。就本文论题而言，我们对发生在金属壁与电介质层之间的传播模式(表面模)最感兴趣。

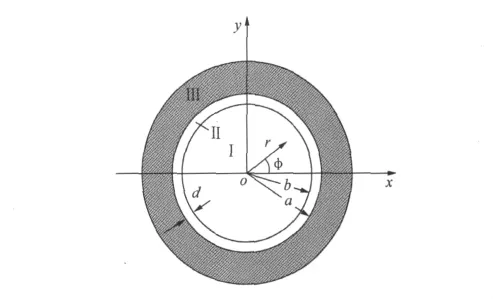
图3 金属壁圆波导内衬电介质层

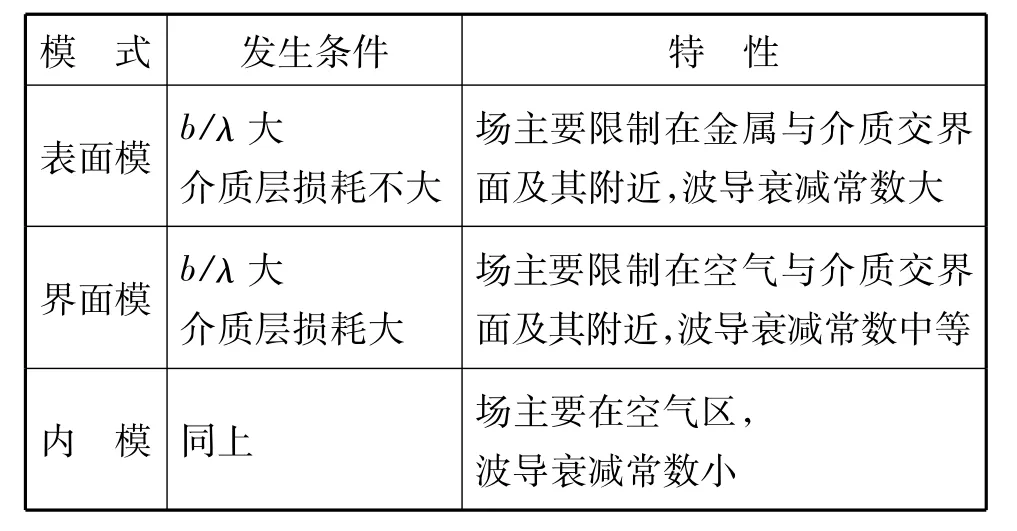
表1 三类模式的发生条件和特性

在内衬均匀介质层的圆过模波导内，可能有好几类简正模。某种模式是否存在，取决于特征方程的解是否接近其存在的条件。不言而喻，当d很小时将主要是。当d较大时，如果介质层的损耗较小，则波导中多数低阶模将变为，衰减不再随d变化;而损耗较大时，则多数低阶模仍为内模。

我们知道，普通的金属壁空波导，在壁电导率为无限大时是TEmn模式群和TMmn模式群，壁电导率为有限值时是HEmn模式群、EHmn模式群。当内壁有介质层，即使壁电导率为无限大，一般也不再有纯TE、TM模，特殊情况下还可以有，那就是:①圆对称(m=0)情况，可有TE0n和TM0n;②介质层无耗，低阶模仍为TE和TM;③靠近截频(fc)的频区，简正模是“准TE”和“准TM”。

上世纪90年代初黄志洵和曾诚［9］针对内衬电介质层圆波导推导出一个新的特征方程，由于假设波导壁电导率为有限、内壁又有内衬介质层，因而具有普遍性。但这个方程式很复杂，这里只写出较简单的式子——如果壁电导率足够大，则普遍特征方程可近似为

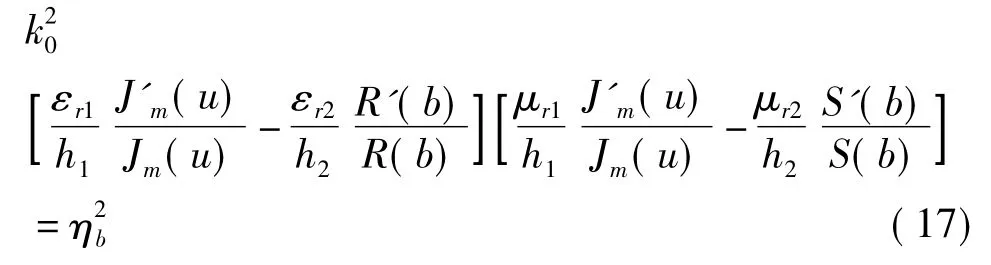
式中εri、μri是i区的相对介电常数、相对导磁率;hi满足

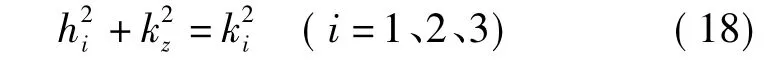
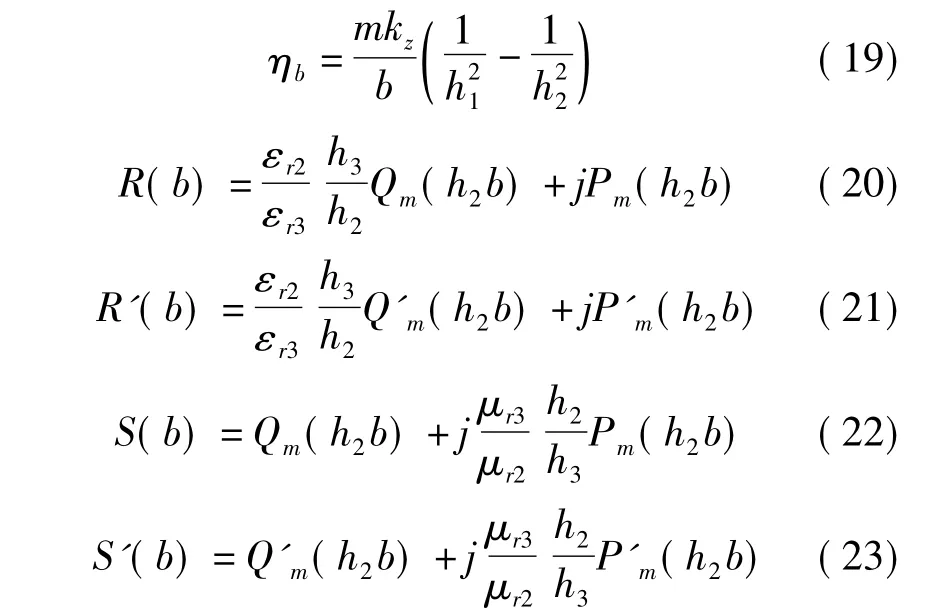
如果介质材料损耗小，h1有很大的正虚部，表明场主要集中在内衬介质层中，简正模成为。这时有:

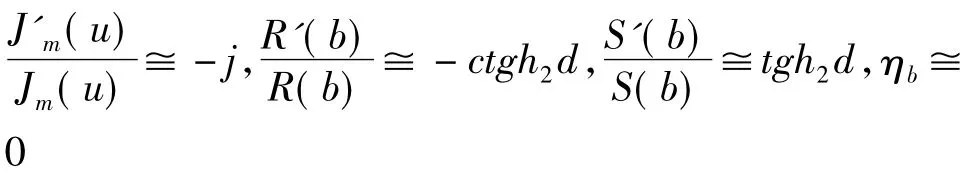
当b/λ足够大时，Imh1变得很大，这时可得进一步简化的特征方程为:

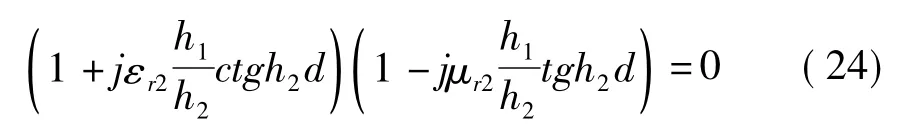
当h1/h2较大时，有

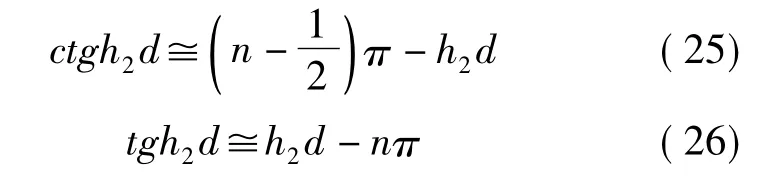
式中 n 为正整数(1、2、3、...);代入后得到 q=h2d的值(取μr2=1):

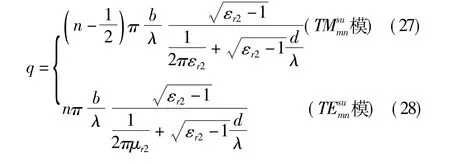
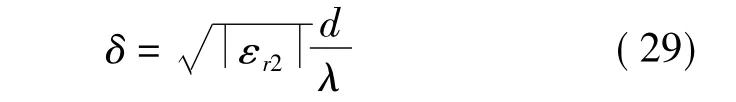
如 εr2较大，则有

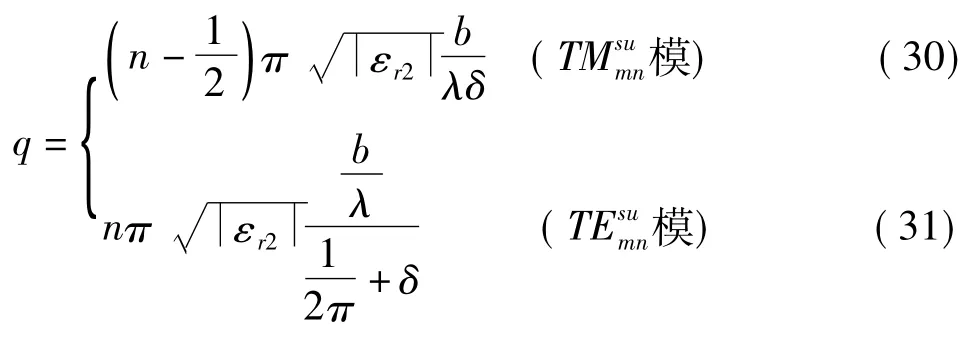
衰减可由下式决定:

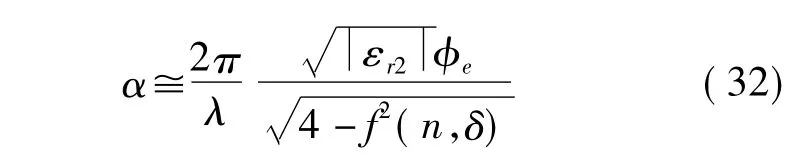
式中

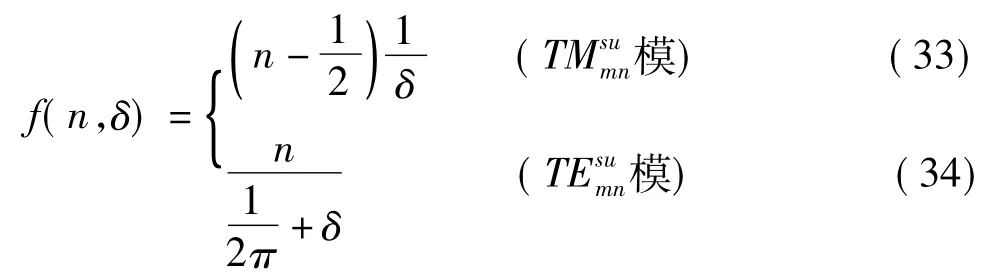
由于(32)式来源于简化的特征方程，所以是近似式。当δ增大到一定程度，可得进一步的近似式:

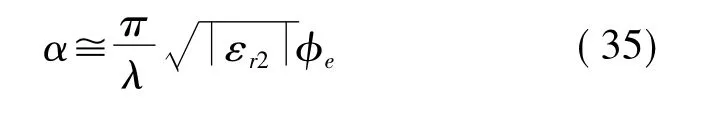
这时衰减与d无关。当然我们仍然可以只用(32)式进行计算，并与电子计算机的结果作比较。表2是模的情况，表3是模的情况;计算时的物理参数均为:金属壁电导率σ=1.6×107s/m，b/λ=3.5，εr2=10∠-5°，μr2=1。

表2 模的衰减常数计算

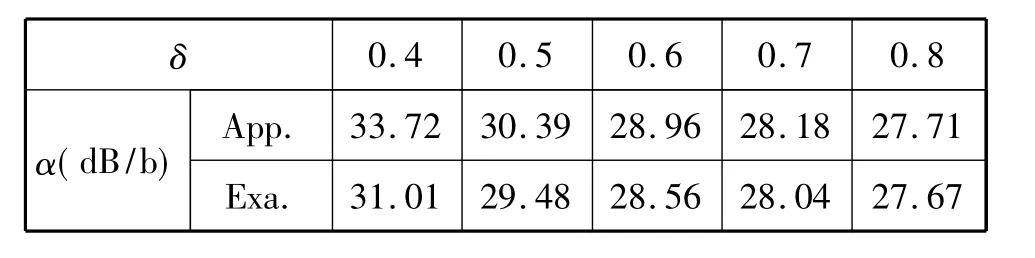
表2 模的衰减常数计算

δ 0.4 0.5 0.6 0.7 0.8 α(dB/b)App. 33.72 30.39 28.96 28.18 27.71 Exa. 31.01 29.48 28.56 28.04 27.67

表3 模的衰减常数计算

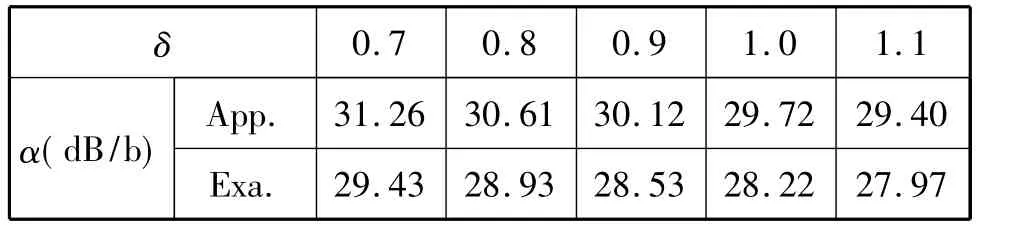
表3 模的衰减常数计算

δ 0.7 0.8 0.9 1.0 1.1 α(dB/b)App. 31.26 30.61 30.12 29.72 29.40 Exa. 29.43 28.93 28.53 28.22 27.97

结论是，当b/λ大、介质层损耗大时，可能存在的主要模式是和。也就是说，当内衬材料损耗及厚度都够大，内径与波长之比也够大，多数简正模将为，场分布主要在空气区，电场、磁场在波导壁附近都小，即能量比较小。

4 金属的介电特性

以上所述均为导波理论中的表面波概念，它有一系列实际应用，例如微波传输中的模抑制器、雷达技术中的RCS抑制等。然而几十年来存在着另一套理论体系和不同的研究路线，即采取表面等离子波(SPW)观点而展开分析、计算和实验。实际上，SPW分析既可应用经典电磁理论中的表面波［10］及消失态［11］概念，又由于下述两方面的原因而可以使用量子理论。首先是波动经由量子化途径成为粒子;其次是玻璃三棱镜技术背后的量子隧穿(quantum tunneling)解释［12］。SPW(SPP)的应用是多方面的，例如特殊的长程SPP波导等器件［13］，集成光学与近场光学，纳米技术等。它是高度综合性的交叉学科，既激起理论家的兴趣又造成技术专家的密切关注。

我们的论述将从金属的介电特性开始。介电常数本来是针对电介质(它们当中不产生传导电流)而提出的概念，用到导体上并不合适。然而金属由以原子核为基础的晶格和自由电子群组成，自由电子群可与等离子体中的自由电子气相类比，因而可把等离子体分析中的参数(如自然谐振频率ωp)引入到分析中。在单色波时，Maxwell第一定律为

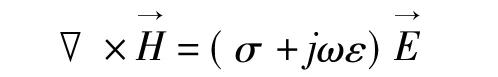
σ是电导率;上式右端第一项是传导电流，第二项是位移电流;此式可写作

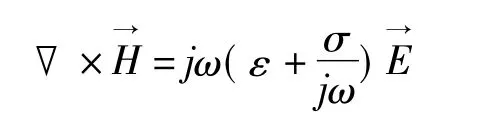
如果取

下标c代表conductor;故方程改写为

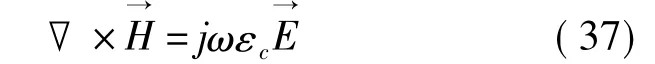
这时εc就成了电导率σ≠0时的取

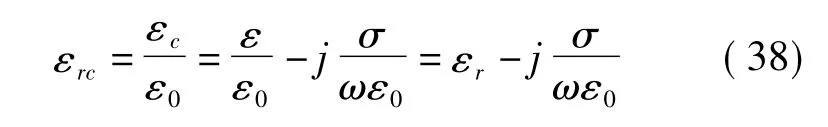
对真空而言(空气也类似)εr=1，这时有

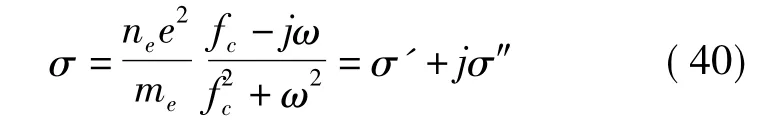
式中e为电子电荷，me为电子质量，ne为电子浓度，fc为动量转移的平均碰撞频率(下标c代表collision);上式所决定的复数电导率称为Lorentz电导。

向金属导体理论中引入等离子体概念是理论发展的重要一步。所谓等离子体振荡频率为

故(40)式成为

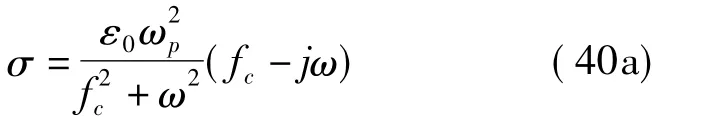
代入到(39)式中，得

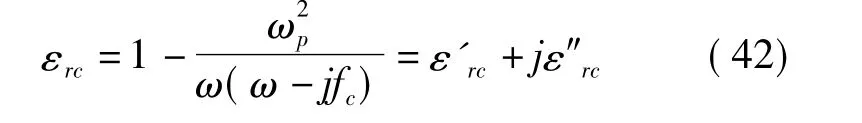
式中

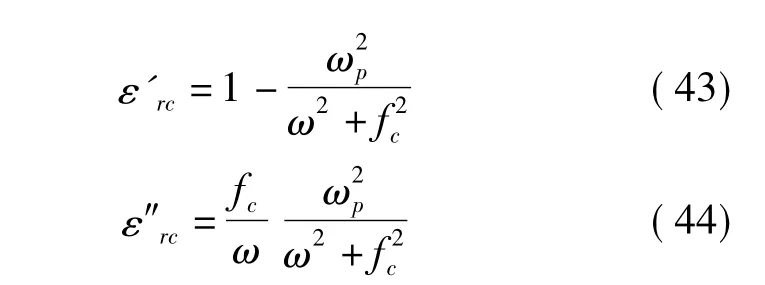
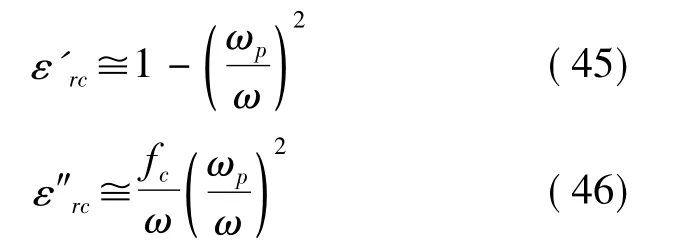
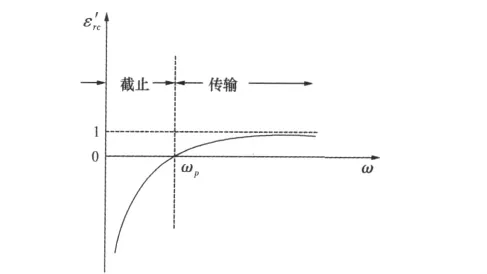
图4 ε'rc与频率的理论关系

在等离子体的传统理论中，得出的方程与(45)式完全相同［14］。这个公式告诉人们:①当ω→∞，ε'rc→1;②当 ω = ωp，ε'rc=0;③当 ω ＜ωp，ε'rc＜0;故可画出图4。由于这是一种高通滤波器特性，ωp很像截止波导理论中的截止频率(ωc)。不过，在等离子体理论描述中，图4纵坐标代表折射率的平方(n2)，这是因为有以下关系式成立:

而科学界对等离子体的描述更多地使用折射率，而非介电常数。

为了便于对不同学科的物理规律作比较，图5画出了一种实在的等离子体(氢等离子体，电子浓度ne=1013cm-3)的情况，实线曲线是电磁波通过时的衰减常数α，虚线曲线是相位常数β，横坐标是频率(104～1013Hz)。在截止区域内电磁场按指数率下降，即消失态;当f＞fp，等离子体呈电介质性状，不是消失态。

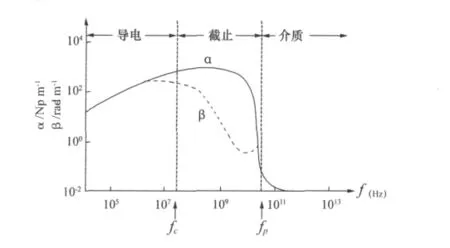
图5 氢等离子体的计算例

以上所述只是把金属中的自由电子群模拟为等离子体，实际上二者有很大的不同。首先，金属的ne比气态等离子体的ne大很多，因而前者的ωp值也大得多。其次，平均碰撞频率fc的值与ne的大小也是有关的，即ne越大fc越大。表4是气态等离子体与固态金属的比较。

表4 气态等离子体与固态金属的参数比较

图4 显示，当 ω ＜ ωp，频率减小时|ε'rc|增大;这意味着波长λ加大时|ε'rc|增大。从文献检索得知，实验是符合这个判断的。图6是一个由对银的测量得到的实验曲线［16］。

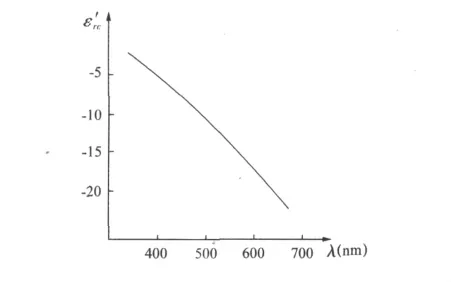
图6 ε'rc与波长关系的实测例子

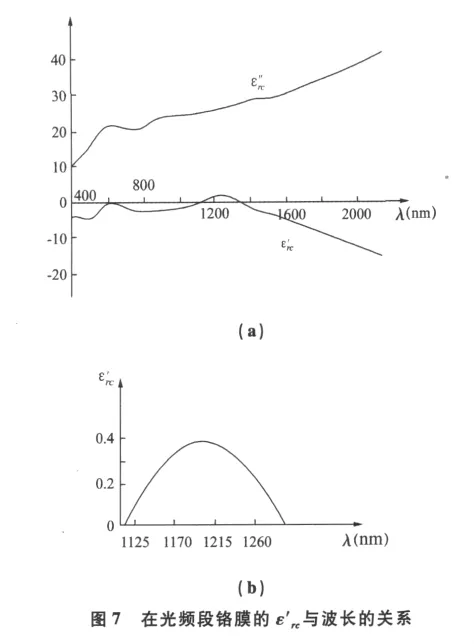
另外，2008 年 M.Sarrazin 和 J.P.Vigneron［17］证明，为了对一些现象作合理解释，不能仅用SPW概念，还要考虑其他的电磁本征模式，特别是出现于金属薄膜的Brewster-Zennek模式［18］，它通过微弱的正介电常数而显示其存在。BZ模明显不同于SPW，它本应出现在介质/介质界面，而非介质/金属界面。图7表示铬膜的情况，虽然在较宽波段上ε'rc＜0，但在一个狭窄波段(λ =1112～1292nm)变为ε'rc＞0。此外，图7显示 ε'rc与波长的关系也不是简单的(波长增加ε'rc减小)的关系，只在波长大于某值(例如1400 nm)时这关系才对。

5 表面等离子波概述

在固体理论中，使用等离子体概念是一种有效的分析方法，即把金属中的自由电子当作高密度电子气体，其体密度可达ne=1023cm-3。这时可把纵向的密度起伏称为等离子振荡(plasma oscilations)，它将在金属内传播开来。单个“体等离激子”(volume plasmon)的能量为［16］

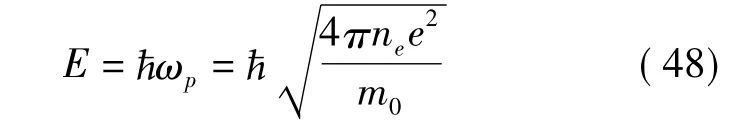
它的值大约为10ev;相应的研究被称为“等离激子物理学”(plasmon physics，PP)。图8是 SPW 的示意，这是一种TM单极化的场，表面场损耗很大，只能传输短距离。

图8 SPW的示意图

SPW分析仍是依靠Maxwell方程组的运用。设按图1选取直角坐标系，即取zy平面是两介质的界面，而z向是表面波传播的方向;相应的场表示式为式中为单位矢量;一个沿z向传播而场在x、-x方向上指数衰减的波，可以写作

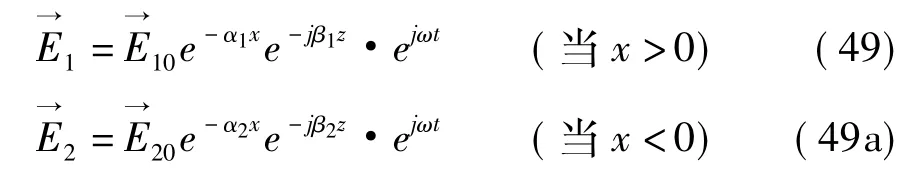
式中α1、α2是衰减常数;对于TM模，在列出场方程并运用边界条件后可以证明有以下方程成立:

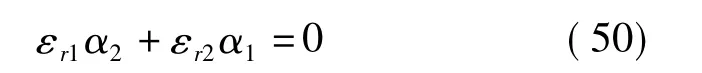
由于α1、α2均为正实数，为了满足上式εr1与εr2的符号应相反——例如若 εr1＞0，要求 εr2＜0;使用金属作为媒质2可满足这一条件。

另一方面，在TE模条件下所作分析得出:

这是不可能满足的，故SPW不能以TE模形式存在。

6 激励SPW的Otto方法

1968年 A.Otto［5］发表论文“用受阻全反射(FTR)法在银中激励非辐射型表面等离子波”，文章描述了在光滑表面上激励SPW的一种新方法，它起因于全反射中的现象。由于在金属/真空界面上相速小于c，用光撞击表面不能激励这种波。然而，如果用一个棱镜使其接近金属/真空界面，可以激励SPW，这是在全反射中存在消失波时用光学方法实现的。可以这样看这种激励:对TM光波反射大大减弱，而入射角是特定的值。此法可以对这些波的色散作准确评价。对银/真空界面的实验结果与金属光学(metal optics)理论作了对比，二者是符合的。

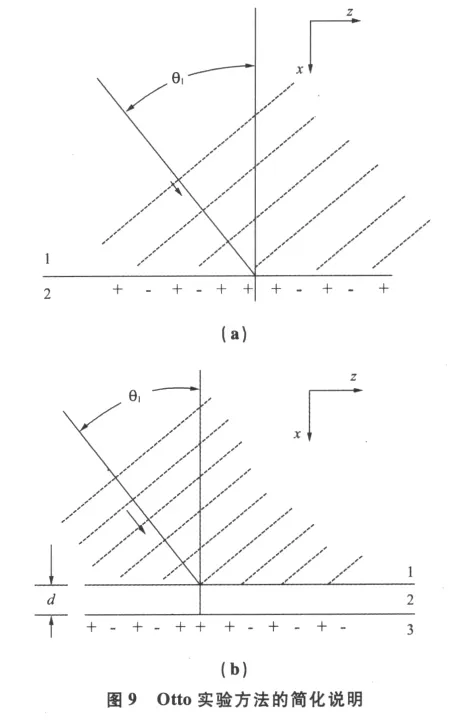
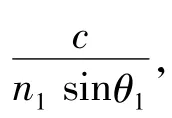
11的相速却小于c/n1。由于相速的差异，图9(a)的方法不能激发SPW。

在图9(b)中有一个间隔层(即区域2)存在。在1区和2区之间的界面上，固定相位点的速度为

现在假如

那么就有

在界面一侧仅为消失波，x方向的场因子为

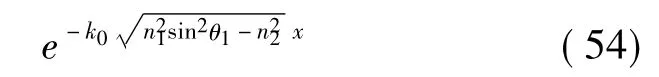
问题是区域2与区域3的界面上会发生什么现象?可以认为这里的SPW会与上述消失波谐振，假如二者的相速相同的话。

现在我们讨论SPW分析中的经典电磁理论的界面方程。我们知道，1947年 F.Goos和 H.Hänchen［20］用实验证实了当光束向界面入射时必将发生的反射波束位移(GHS)。实际上，无论GHS研究，或是1968年A.Otto［5］对电介质与金属界面上发生的表面等离子波(SPW)研究，都与受阻全反射(Frustrated Total Reflection，FTR)密切相关，而且都有消失态(evanescent states)的存在。

2009年黄志洵［21］在论文“消失态与 Goos-Hänchen位移研究”中，给出了对电磁波在不同媒质界面的折射和反射的分析，进而讨论了界面发生全反射时的消失态表面波。我们现在从此文中已有的推导出发，建立起反映界面情况基本方程，并与Otto文章中的表述相对照。该文在分析由P点发出的波束向媒质1、2的交界面入射(图10)时指出，入射角θ1不断增大到超过临界角(θ1c)时就发生全反射，过程①→②→③;给出媒质2中的电场为

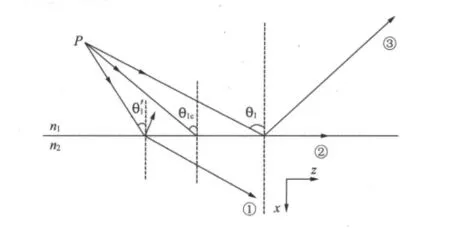
图10 两媒质界面上的全反射

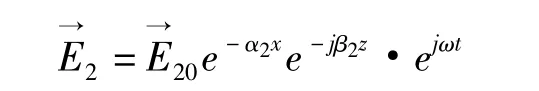
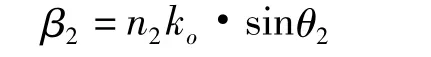
这个行波的振幅在x方向是指数衰减的，即消失态。也就是说，e-α2x代表其振幅，衰减常数为

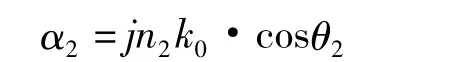
进一步的推导证明:

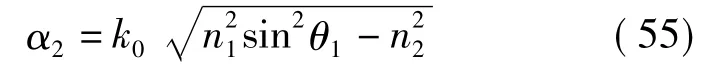
由于θ1是入射波束与界面法向的夹角，取θ1=π/2时有

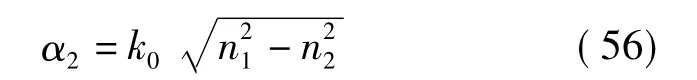
对无磁性媒质而言折射率n与介电常数εr关系为n，故从形式上将有以下方程:

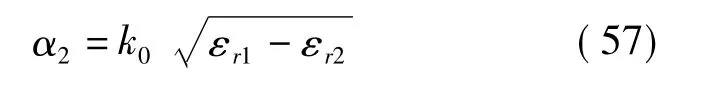
现在来看 Otto的分析;他用时谐因子 e-jωt，但在本质上不会有所不同。取媒质1(图8上半部分)的电介质，相对电介常数 εr1＞0;媒质2为金属(图8 下半部分)，相对电介常数 εr2= ε'r2+jε″r2，而ε'r2＜0;对于 x＞0，有

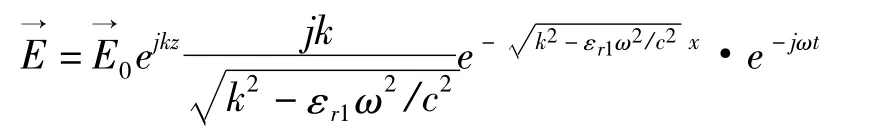
也就是

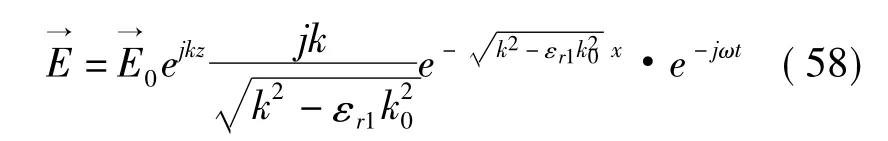
对于 x＜0，有

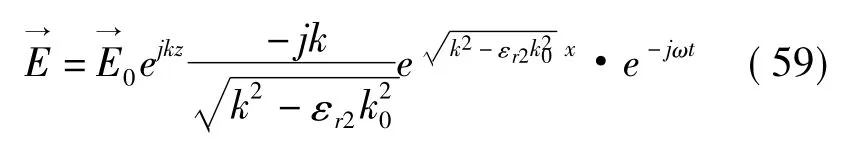
现在，z方向是简谐波(频率ω，波数 k);在界面两侧，场是消失态(evanescent)。这意味着

而相速v=ω/k比介质中的平面波波速要小。另外又有

而 ε'r2＜0。

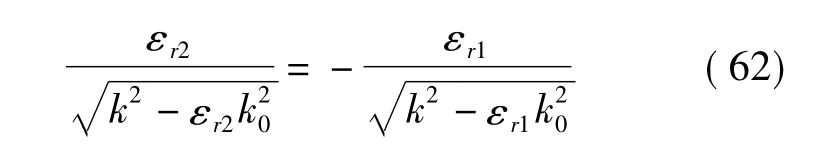
上式决定了整个体系的色散关系k(ω)。

下面给出在TM模条件下讨论时Zenneck类型SPW传播时的色散关系。在过去的讨论中，场的时间相位因子可取 exp［jωt- γz］或 exp［-jωt+ γz］;当取后者时，若忽略衰减(γ=α+jβ≅jβ)就有 exp［-jωt+jβz］。现在 β 也是复数，可写 β = β'+jβ″，并可证明［15］

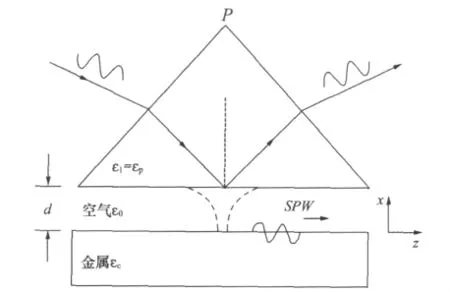
图11 Otto的SPW激励方法(原理)

Otto实验的原理建筑在“被衰减的全反射”(attenuated total reflection，ATR)的基础上，意思是说利用单三棱镜、通过调整入射角使之发生全反射时，底面有消失波渗透到下面的介质中，如图11所示。如棱镜P的折射率足够大，对于TM入射波可以调整入射角(θ1)使入射波沿界面方向的波矢分量等于SPW要求的波矢，调整空气隙厚度d也有影响(d应当足够小)，而这时消失波沿x方向的强度为

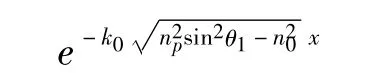
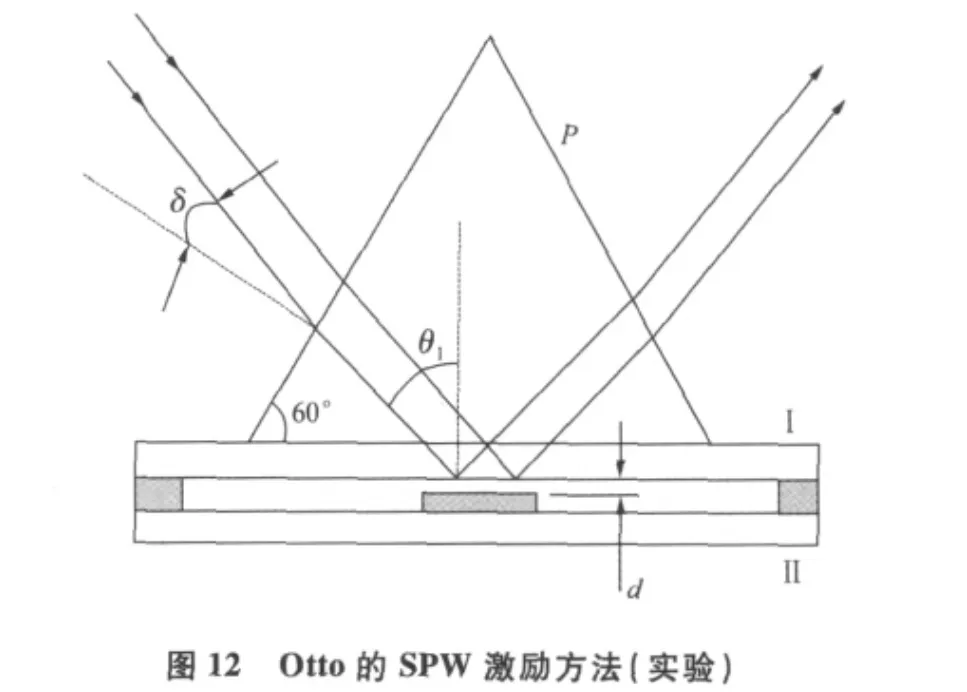
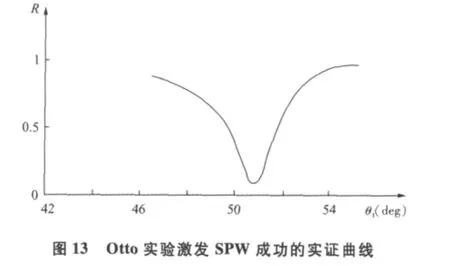
式np中是棱镜折射率，n0≅1是空气折射率;这个消失波将与金属表面SPW谐振(如二者相速相等)，亦即SPW被激发。这时由于SPW的能量被吸收，对特定入射角全反射“受阻”。测量会发现由棱镜底部的全反射波强(光强)明显下降，形成一个吸收峰，就证明使用ATR技术激励SPW成功。图12是Otto实验的示意，P是石英玻璃制成的;Ⅰ、Ⅱ是石英玻璃板，面积为 9.5×5cm2，板Ⅱ中间 0.7×1.5cm2面积是镀银膜，厚度大于100nm;图13是实验结果举例，纵坐标表示反射的大小;实验条件是:金属膜厚150nm，入射光波长λ=406nm。实验显示，当调整入射角使θ1为一合适角度(有文献称之为θATR)，SPW被入射波激发，这时入射能量的很大部分转移到金属膜与空气的界面上，成为SPW的能量;故反射率R这时成为最小值(负峰值)，表示“全反射”已有名无实，也可称之为谐振吸收峰。故能否获得图13那样的曲线是实验激励SPW是否成功的标志!

7 激励SPW的Kretschmann方法

1971 年 E.Kretschmann［6］发表了题为“用表面等离激子激励以确定金属光学常数”的论文，给出了精确决定金属薄膜的光学常数和厚度的方法，它基于光波全反射条件下激起的SPW;在λ=400～600nm波段对银箔进行了测量，给出了方法的精度。图14是Kretschmann的SPW激励方法示意，方便之处在于金属膜可以直接镀在三棱镜的底面上。可能是由于Kretschmann的方法简单易行，在上世纪80年代就广泛被用来确定薄金属膜的光学常数和厚度，成为一种技术［22，23］。

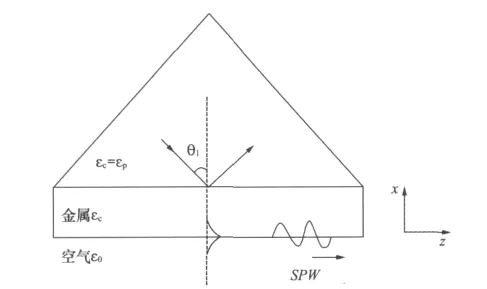
图14 Kretschmann的SPW激励方法(原理)

Kretschmann说，虽然Otto最先提出了用棱镜激发SPW的方法，但在棱镜与金属之间有薄空气层的安排，对测量介电常数是不利的，特别是测量时空气层厚度难于掌握。我们用本文的符号εrc=ε'rc+jε″rc来表达 Kretschmann 的思路——他指出，如果金属的介电常数满足以下不等式:

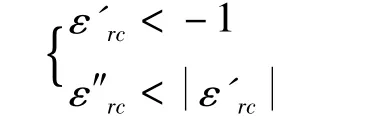
那么非幅射性的SPW可能出现在金属与空气的介面上，SPW的特点是，波矢的水平分量k⊥＞k0;把TM极化光射到棱镜面(已直接镀有薄金属膜)上，且θ1＞θ1c，可以激励 SPW。具体讲，改变 θ1可找到反射最小的位置，测量谐振角可计算出εrc。而且，反射率Rp最小时，吸收率Ap=1-Rp可达到最大，膜厚可由下式得出:

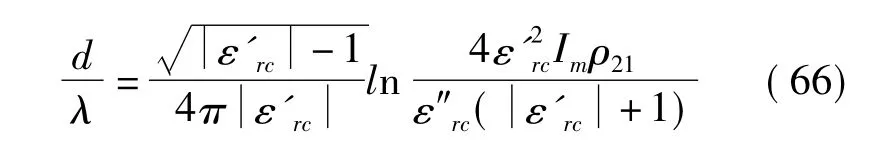
式中

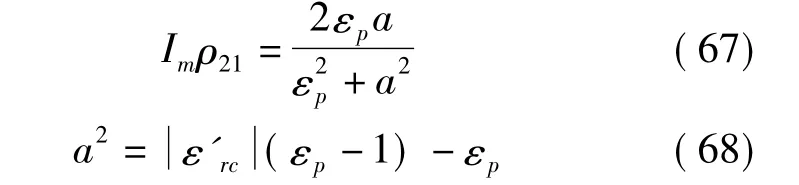
8 讨论

近年来对表面电磁波的研究重新引发了科学工作者们浓厚的兴趣，这不是偶然的。首先，开波导中的慢波(或闭波导中加入电介质后产生的慢波)造成了许多物理学方面的思考，涉及波动力学中的一些根本性问题。其次，对金属的介电常数的研究，以及对SPW激励方法的研究，开拓了人们的科学思维，刺激了一些交叉学科的生成。

现对当前的研究趋向这里作简要的讨论。首先在微波用三棱镜技术激励SPW的可能性问题是令人感兴趣的。虽然2001年 H.E.Went和 J.R.Sambles［19］曾给出用金属光栅(metallic gratings)技术在微波激发SPP的方法，2004年、2009年又陆续有人做了这方面的实验［15，24］;然而至今尚未看到采用棱镜方法的报导。我们认为在微波按Otto型方法作实验是有可能成功的，有关尝试已在进行。

另外，浙江农林大学教师王仲钺于2010年9月5日发email给黄志洵说:“读了您的文章‘表面波波导理论的研究’一文后，觉得表面电磁波色散关系其实与快子(超光速粒子tachyon)的能量方程完全对应，差别只在于一个比例系数。......表面波的相速小于光速，正好说明真实速度大于光速——这是量子力学中的物质波理论的决定的，真实运动速度与相速乘积为一常数(c2)。总之，开波导与闭波导不同，色散关系对应的是快子方程!可以考虑做表面波实验研究这一问题。”……王仲钺还用“踏破铁鞋无觅处，得来全不费功夫”的诗句描写他的心情和感受。

de Broglie物质波理论中确有下述公式［25］:式中v是微观物质粒子(如电子、原子)的运动速度，动量为mv;vp是该粒子对应的物质波的相速。从这里出发思考，王仲钺的意见是有道理的，进一步的深入研究则尚待进行。

［1］ Sommerfeld A.Fortpslanzung elektrodynatischer wellen an einem zykindrischen leiter［J］.Ann.d.Phys，1899，67(2):233-237.

［2］ Harms F.Electromagnetishe wellen an einem draht mit isoliesender zylindrischen huelle［J］.Ann.d.Phys，1907，23(1):44-49.

［3］ Hondros D，Debye P.Elektromagnetishe wellen an dielektrischen draehten［J］.Ann.d.Phys，1910，32(3):465-470.

［4］ Goubau G.Surface waves and their application to transmission lines［J］.Jour.Appl.Phys，1950，21(8):1119-1122.

［5］ Otto A.Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection［J］.Zeit.für Phys，1968，216:398-410.

［6］ Kretschmann E.Die bestimmung optischer konstanten von metallen durch anregung von oberflächchenplasmaschwingungen［J］.Zeit.für Phys，1971，241:313-324.

［7］ 黄志洵.截止波导理论导论(第二版)［M］.北京:中国计量出版社，1991.

［8］ 黄志洵，曾诚.内衬电介质层过模圆波导的研究［J］.光纤与电缆，1989，(5):12-17.

［9］ Huang Z X，Zeng C.The general characteristic equation of circular waveguides and its solution［J］.Jour.China Univ.of Sci.＆ Tech.，1991，21(1):70-77;又见:Huang Z X，Zeng C.Attenuation properties of normal modes in coated circular waveguides with imperfectly conducting walls［J］.Microwave ＆ Opt Tech Lett，1993，6(6):342-349.

［10］ 黄志洵.表面波波导理论的研究［J］.北京广播学院学报(自然科学版)，2005，12(3):1-13.

［11］ 黄志洵.论消失态［J］.中国传媒大学学报(自然科学版)，2008，15(3):1-19.

［12］ Nimtz G，Heitmann W.Superluminal photonic tunneling and quantum electronics［J］.Prog Quant Electr，1997，21(2):81-108.

［13］ Sarid D.Long-range surface plasma waves on very thin metal films［J］.Phys，Rev Lett，1981，47(26):1927-1930.

［14］ 黄志洵.波在电离气体中的截止现象和消失场特性.见:超光速研究——相对论、量子力学、电子学和信息理论的交汇点［M］.北京:科学出版社，1999.

［15］ 王亮.薄层等离子体与表面等离子体激发的实验研究［C］.中国科学技术大学博士论文，2009.

［16］ Raether H.Surface plasmons［M］.Berlin:Springer-Verlag，1988.

［17］ Sarrazin M，Vigneron J P.Light transmission asisted Brewster-Zennek modes in chromium films carrying a subwavelength hole array［J］.Phys.Rev，2008，B71(7):075404-075408.

［18］ Zennek J.Uber die fortpflanzung ebener elektromagnetischer wellen langs einer ebenen leiterflache und ihre beziehung zur drahtlosen elegraphie［J］.Ann.d.Phys，1907，328(10):846-850.

［19］ Went H E，Sambles J R.Resonantly coupled surface plasmon polaritons in the grooves of very deep highly blazed zero-order metallic gratings at microwave frequencies［J］.App.Phys Lett，2001，79(5):575-577.

［20］ Goos F，Hänchen H.Ein neuer fundamentaler versuch zur total reflexion［J］.Ann.d.Phys，1947，6(1):333-346.

［21］ 黄志洵.消失态与Goos-Hänchen位移研究［J］.中国传媒大学学报(自然科学版)，2009，16(3):1-14.

［22］ Chen W P，Chen J M.Use of surface plasma waves for determination of the thickness and optical constants of thin metallic films［J］.Jour.Opt.Soc.Am.，1981，71(2):189-191.

［23］ Yang F.Use of exchanging media in ATR con-figurations for determination of thickness and optical constants of thin metallic films［J］.App.Opt，1988，27(1):11-12.

［24］ Akarca-biyikli S S.Resonant excitation of surface plasmons in one-dimensional metallic grating structures at microwavefrequencies［J］.Jour.Opt.A，2005，7:5159-5164.

［25］ 黄志洵.波动力学的发展［J］.中国传媒大学学报(自然科学版)，2008，15(4):1-16.