反作用飞轮非理想电磁力矩对卫星姿态的影响

陈 霞，邹继斌

(哈尔滨工业大学机器人技术与系统国家重点实验室，150001哈尔滨，xia.chen@johnsonelectric.com)

反作用飞轮是卫星姿态控制系统采用的主要执行部件之一，具有控制精度高、结构简单等优点，广泛应用于卫星的高精度姿态控制系统［1］.

反作用飞轮主要包括大惯量轮体、飞轮电机、驱动器及密封外壳.反作用飞轮工作时，会产生某些非理想力矩，这些非理想力矩主要由飞轮不平衡、轴承摩擦、飞轮电机结构及驱动器误差等产生［2-5］.4种非理想力矩中，飞轮不平衡力矩和轴承摩擦力矩对卫星姿态的影响较大，关于不平衡力矩的建模及摩擦力矩抑制的研究较多.随着现代卫星控制精度要求逐步提高，飞轮电机结构及驱动器误差所产生的非理想力矩对卫星姿控的影响也不容忽视，针对这2种非理想力矩进行研究.

目前飞轮电机普遍采用定子无铁芯结构的无刷直流电机［4-5］，与传统的无刷直流电机相比，其定子采用不导磁的材料.此结构可以彻底消除定位力矩，但仍存在力矩波动.文献［4］采用傅里叶级数形式建立了力矩波动的模型，并提出了力矩波动近似的建模方法，反作用飞轮的驱动器使飞轮电机根据给定力矩加速或减速，实现四象限闭环控制.由于驱动电路及控制方案的选择，反作用飞轮的电枢电流有可能偏离给定值，发生瞬时的跳动，产生力矩跳动［5-7］.文献［5］指出美国ITHACO公司的反作用飞轮通过合理设计驱动器，可以消除力矩跳动，但没有方案介绍.国内学者对力矩跳动的抑制也进行了一些研究［6-7］，但仍不能完全解决.力矩波动、力矩跳动都属于电磁力矩的范畴，所以称其为非理想电磁力矩.

本文分析了反作用飞轮存在的2种非理想电磁力矩的产生机理，以某型轮控微小卫星姿态控制系统为例，通过数学仿真的方法，研究反作用飞轮非理想电磁力矩对卫星姿态的影响.

1 反作用飞轮非理想电磁力矩

反作用飞轮的电磁转矩为

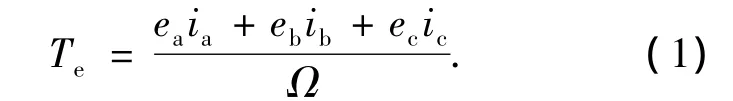
式中:ea、eb、ec分别为飞轮电机三相绕组的反电势;ia、ib、ic分别为飞轮电机三相绕组的相电流.

1.1 力矩波动

力矩波动是由于飞轮电机的非理想反电势造成的.图1为A相绕组导通时的电路拓扑图，U为加在绕组两端的电压，Ra为A相绕组电阻，La为A相绕组电感，ea为A相绕组反电势.由于反作用飞轮通常为定子无铁芯的结构，绕组的电感值很小，有La≈0.

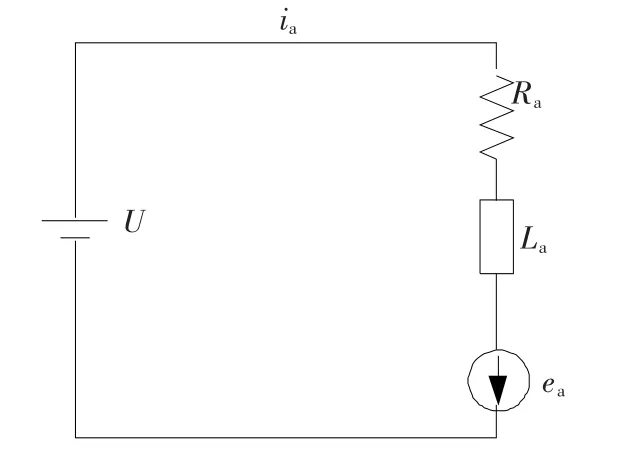
图1 A相绕组导通时电路拓扑

此时，A相绕组产生的电磁转矩Ta为

式中Ω为飞轮电机转速.

当期望输出恒定的电磁转矩时，A相绕组导通期间，加在绕组两端的电压U为恒定值，若A相绕组的反电势为恒定值，由式(2)可知，A相绕组产生的电磁转矩为理想的恒定值，此时，A相绕组的电磁力矩不存在非理想力矩，三相绕组轮流导通产生的合成电磁转矩也就不存在非理想力矩.可见，理想的绕组反电势应为梯形波.

由于磁钢充磁不充分，永磁体不能产生梯形磁密，再加上绕组不对称、永磁体不光滑等工艺问题，反电势通常不是理想的梯形波(图2)，此时，由式(2)可得，飞轮电机的电磁转矩不再理想.由非理想反电势所产生的非理想电磁转矩为力矩波动.

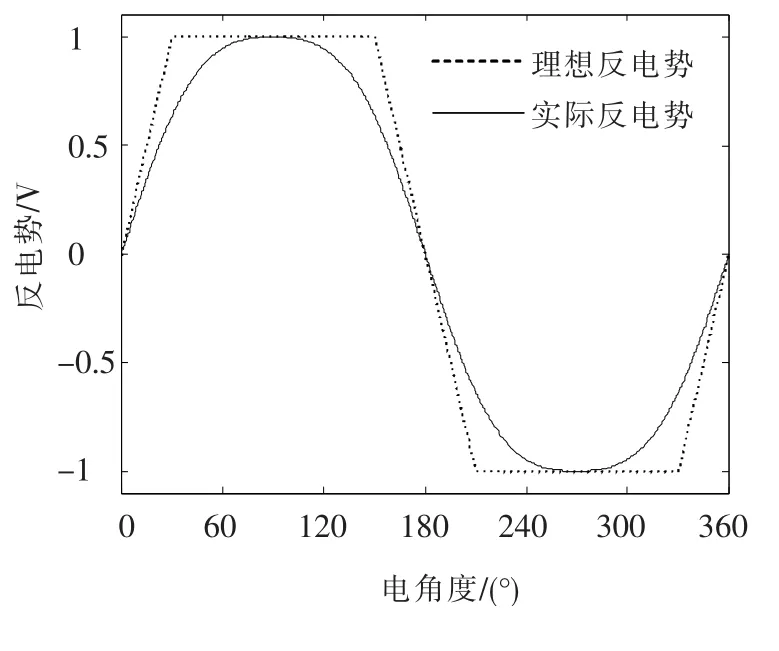
图2 理想反电势与实际反电势

图3为力矩波动的示意图，可见力矩波动是随电机位置呈周期变化的.

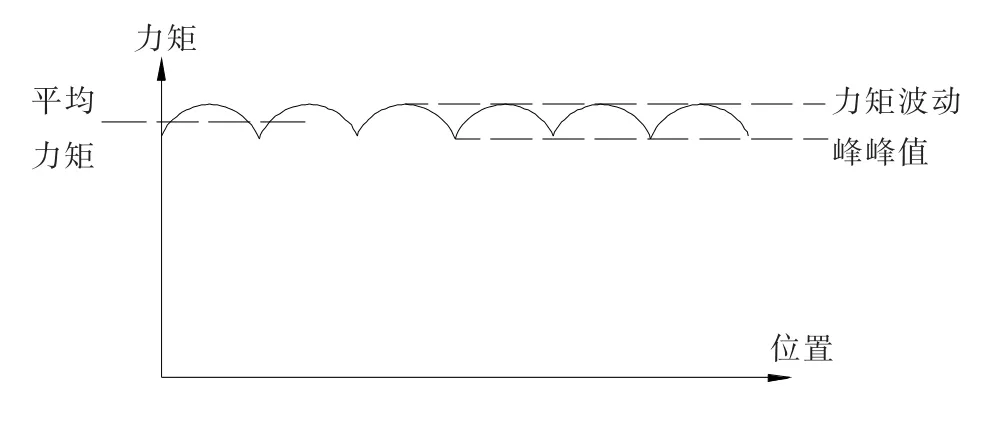
图3 力矩波动示意

力矩波动的大小由力矩波动系数FTR衡量.

式中:Tp-p为力矩波动的峰峰值;To为平均力矩.

力矩波动与电机转子位置一一对应，其波动频率与换相方式及电机极对数有关.三相P对极电机，三相六态换相方式时，力矩每个电周期波动6P次;三相三态换相方式时，力矩每个电周期波动3P次.力矩波动的频率fr可表示为

式中P为极对数，K与换相方式有关，三相三态换相方式时，K=3;三相六态换相方式时，K=6.

1.2 力矩跳动

反作用飞轮驱动器保证电机在四象限运行过程中力矩能够跟随给定力矩.当给定力矩方向改变，或飞轮转速过零时，电机驱动器需改变换流次序或者改变电流方向.驱动器控制方案的误差会导致力矩跳动.本节以文献［7］的驱动方案为例，分析力矩跳动的产生及影响因素.

文献［7］中采用三相三状态的驱动方式，主回路为三相星接的半桥结构.电动运行时，每相绕组在其反电势的正向120°导通，桥臂采用PAM脉宽调幅控制，此时，飞轮的平均电磁力矩Tea为

式中:Ke为反电势系数，ρ为桥臂串联功率管的占空比，VDC为主回路直流电源电压，R为相绕组电阻.

当电机进入制动状态时，换向控制逻辑推迟180°电角度，使每相绕组在反电势的负半周120°导通，在控制桥臂调整管的同时，对每相绕组的功率管进行PWM控制.此时，飞轮的平均电磁力矩Teb为

式中ρ1为每相绕组串联功率管的占空比.

由式(5)和式(6)可知，若电机从电动状态进入制动状态，ρ和ρ1控制不当可能会产生力矩的跳动;若电机从制动状态进入电动状态，此时转速过零，电机的电磁转矩存在一个必然的跳变，力矩跳动ΔTer可表示为

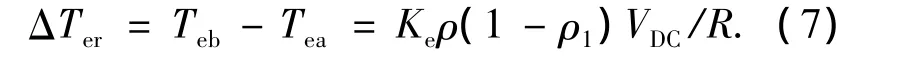
图4为采用此驱动方案时反作用飞轮四象限运行时力矩和转速的实验曲线.飞轮的给定力矩为+0.17 N·m，持续4.2 s后变为-0.17 N·m.可见，飞轮力矩能够跟随给定力矩变化，但存在力矩跳动.

图5为图4的局部放大图.图5(a)为图4中3.9～4.5 s的力矩波形放大图，飞轮力矩变为负值时飞轮进入制动状态，此时力矩跳动值为0.15 N·m，是给定力矩的88.2%.图5(b)为图4中7.9～8.2 s的力矩波形放大图，飞轮转速过零时由制动切换到电动状态，此时力矩跳动值为-0.89 N·m，是给定力矩的5.23倍.

2 轮控微小卫星姿控系统模型

分析的微小卫星为立体测绘卫星，该卫星在正常运行段的大多数时间内，基本上处于对日定向三轴稳定状态，以稳定地获得足够能量.经过目标上空时，进行姿态机动，使CCD相机处于对地定向三轴稳定状态.当拍照结束后，卫星机动回到原来的对日定向三轴稳定状态，继续积蓄能量.此过程中，卫星的姿态稳定和姿态机动均采用反作用飞轮控制.

针对微小卫星对地定向三轴稳定的状态，采用Matlab的Simulink模块建立的姿控仿真模型见图6.

图4 反作用飞轮四象限运行实验波形

图5 反作用飞轮实验曲线局部放大

图6 三轴稳定姿态控制系统框图

三轴姿态控制算法采用PID算法，姿态运动学方程采用旋转四元数描述，具体见文献［8］.

仿真模型的具体参数［9］

1)初始条件

初始姿态角速度:［0.01 0.01 0.01］T(°)/s;

初始姿态角:［1°1°1°］T.

2)系统参数

卫星转动惯量:

轨道角速度:ω0=0.001 107 rad/s;

环境扰动力矩:

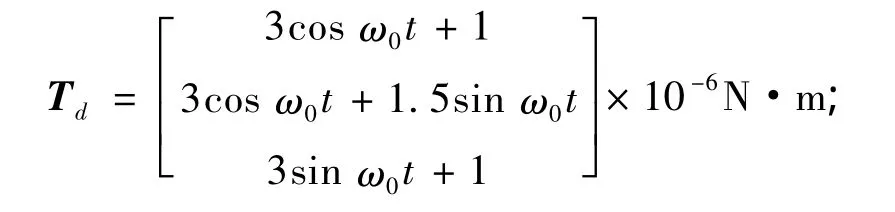
滚动轴PID参数:(1.44，3.847，0.05);

俯仰轴PID参数:(1.512，4.039，0.05);

偏航轴PID参数:(1.645，4.394，0.05).

3)反作用飞轮参数

反作用飞轮转动惯量:J=0.01 kg·m2;

最大转速:2 500 r/min;

最大输出力矩:0.05 N·m;

最大角动量:2.5 N·m·s.

4)控制目标

给定姿态角:［0°0°0°］T;

姿态角速度≤［1 1 1］T×10-4(°)/s;

姿态角偏差≤［0.01°0.01°0.01°］T.

图7为卫星姿态机动仿真曲线，可见60 s后卫星的姿态角速度和姿态角均能满足控制目标，进入对地定向稳定状态.

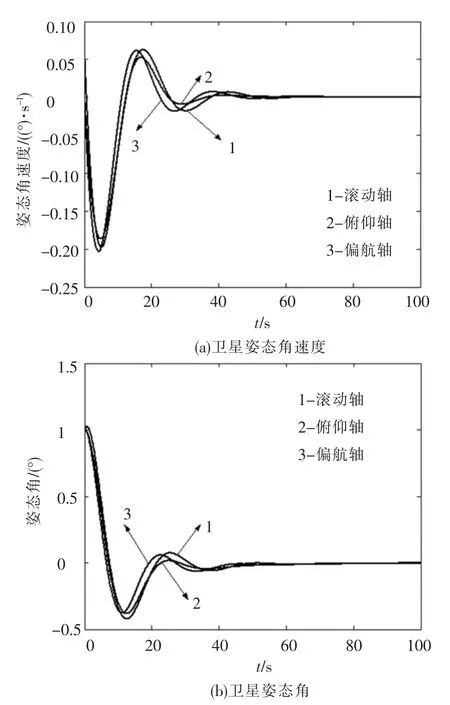
图7 卫星姿态机动仿真曲线

3 非理想电磁力矩对卫星姿态稳定的影响

当卫星进入对地稳定状态后，反作用飞轮的输出力矩主要来克服环境干扰力矩，保持卫星姿态的稳定.本节假设卫星滚动轴上反作用飞轮存在非理想电磁力矩，通过仿真的方法分析其对卫星滚动轴姿态角和姿态角速度的影响.

3.1 力矩波动的影响

假设反作用飞轮的反电势仅含基波(正弦波)及反电势含有基波和三次谐波，在同一转速下，两种反电势波形如图8所示.可见含有3次谐波后反电势平顶宽度增加.

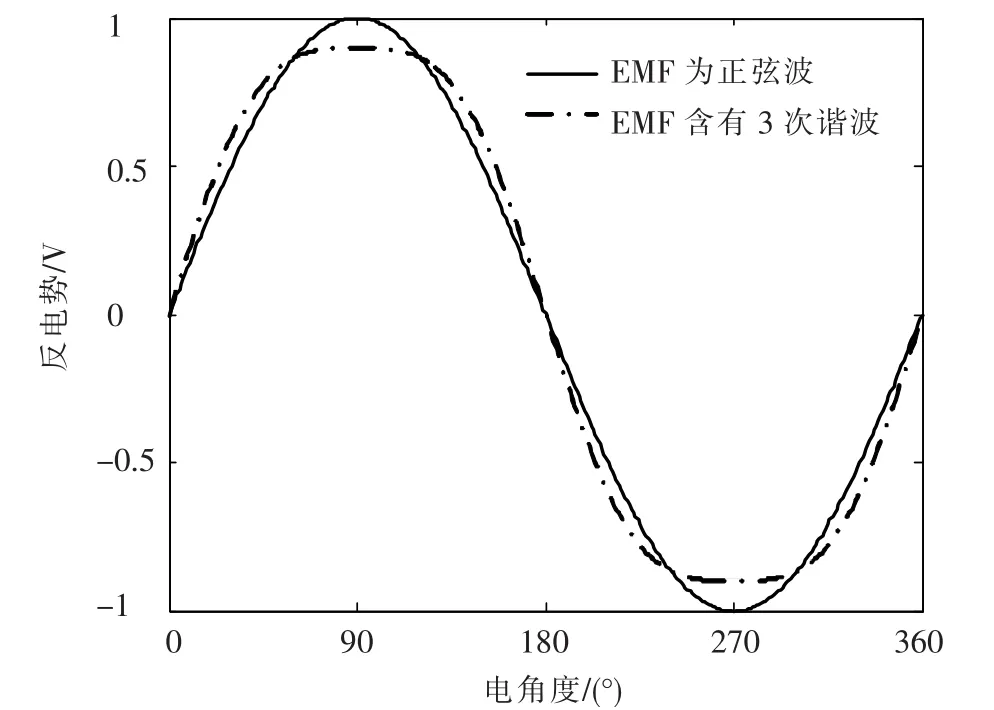
图8 反电势波形对比

图9为反电势不同时，反作用飞轮力矩及转速的仿真波形.反电势为正弦波时，力矩波动系数为25%;反电势含有三次谐波后，力矩波动系数降为16%，可见反电势的平顶宽度越大，力矩波动系数越小.力矩波动的频率随电机转速的减小而降低，转速过零时力矩波动的频率最低.由于飞轮惯量较大，两种情况下飞轮转速差距较小.

图9 反电势不同时飞轮的力矩波动与转速

图10为反电势不同时，力矩波动对卫星姿态的影响.力矩波动使卫星姿态发生同频率波动;当飞轮转速过零时，力矩波动对卫星姿态的影响最大;力矩波动系数增加，力矩波动对卫星姿态影响变大.当力矩波动为25%时，力矩波动使卫星姿态角速度最大偏差2×10-4(°)/s，超过稳定控制指标.

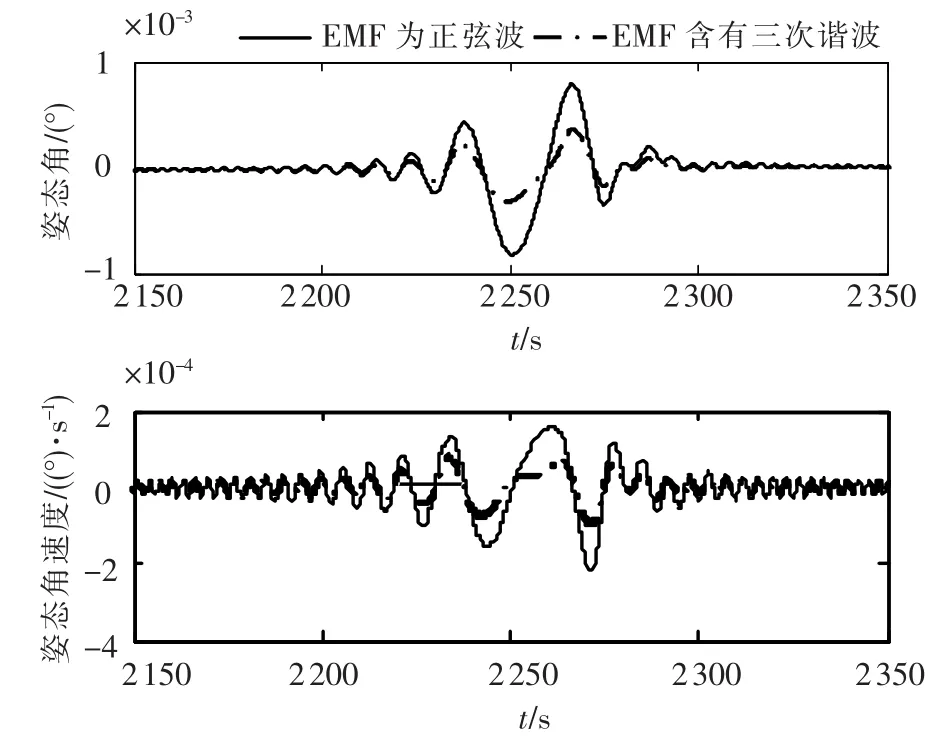
图10 反电势不同时力矩波动的影响

图11为反电势相同，飞轮电机极对数不同时，力矩波动对卫星姿态的影响.极对数增加，力矩波动的频率增加;低频的力矩波动对卫星姿态的影响较大.

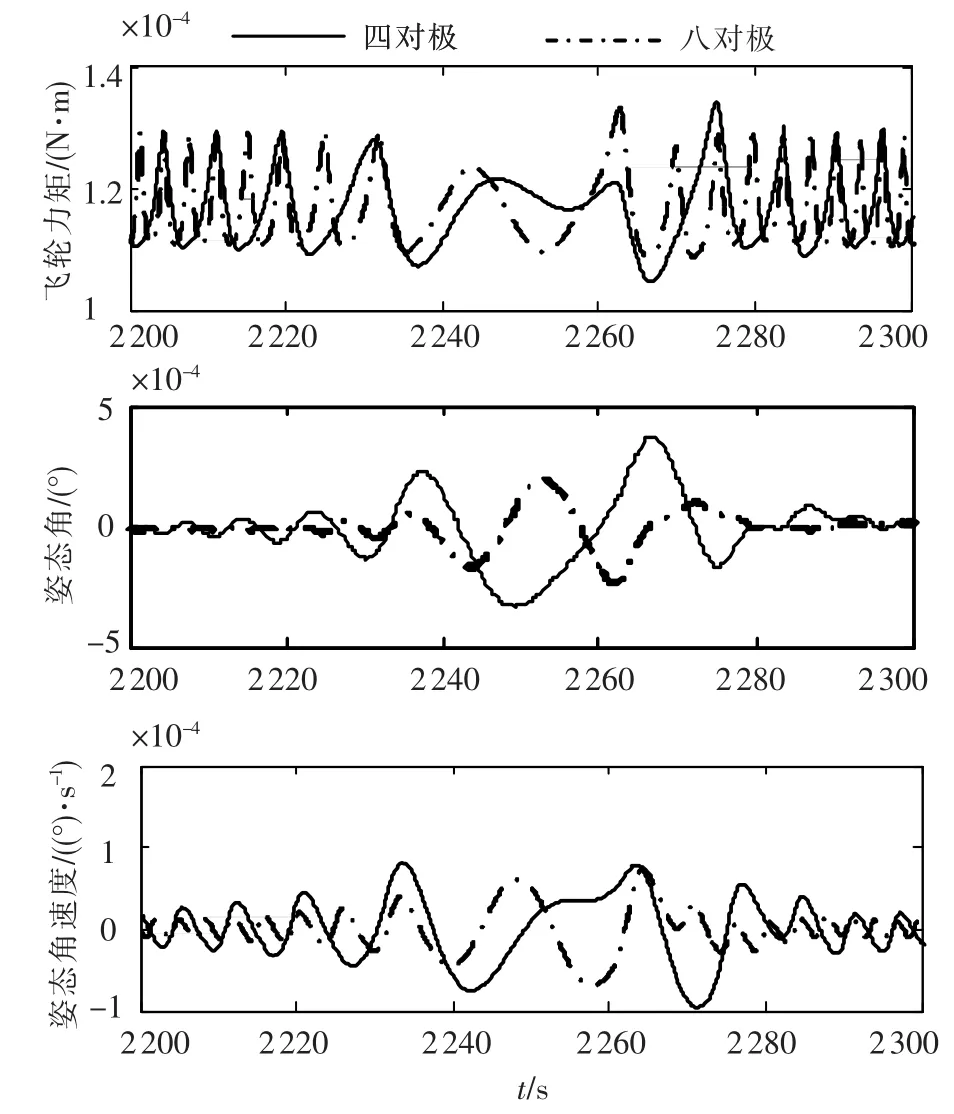
图11 飞轮极对数不同时力矩波动的影响

3.2 力矩跳动的影响

假设在转速过零时刻力矩跳动幅值为飞轮最大力矩的20%，持续时间10 ms，此时卫星姿态角速度和姿态角见图12.力矩跳动使卫星姿态发生跳变，卫星姿态角速度最大偏差2.92×10-4(°)/s，超过稳定控制指标.

力矩跳动与反作用飞轮的驱动方案有关，其跳动幅值可为最大力矩的0%～100%，跳动持续时间可为零点几毫秒到几十毫秒.图13为力矩跳动幅值、跳动持续时间与卫星姿态最大偏差值的关系，图13(a)中z轴为姿态角最大偏差，图13 (b)中z轴为姿态角速度最大偏差.可见，随着力矩跳动幅值和跳动持续时间的增加，卫星姿态的最大偏差增大.此系统若跳动幅值等于最大力矩、跳动持续时间10 ms时，姿态角速度最大偏差为1.5×10-3(°)/s，超过稳定控制指标.

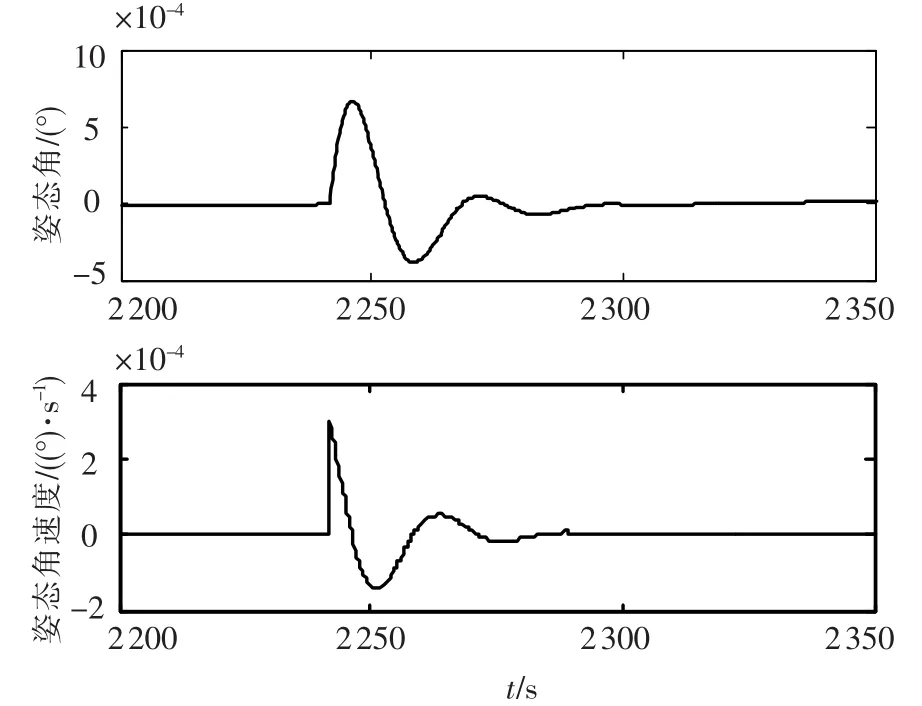
图12 力矩跳动对滚动轴姿态的影响

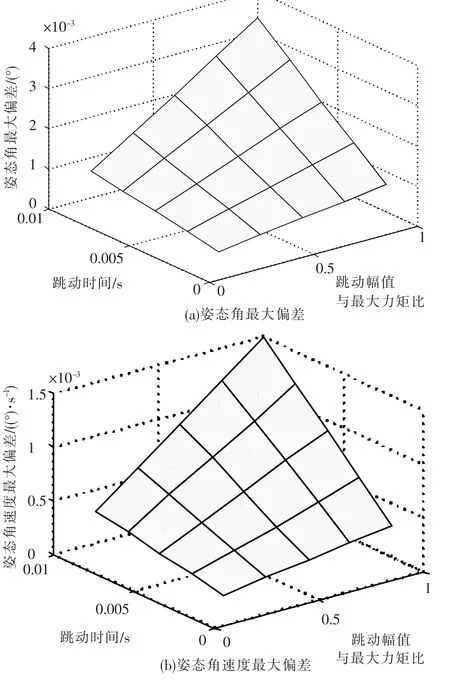
图13 力矩跳动与卫星姿态最大偏差的关系

4 非理想电磁力矩的抑制

4.1 力矩波动的抑制

由于力矩波动在低频时对卫星姿态影响较大，尤其是飞轮过零期间，可设置飞轮工作在偏置状态，在某一转速附近加速或减速，避免飞轮转速过零.此时，卫星一般配置4个飞轮，通过飞轮空间分布的配合，保持卫星的整体动量为零.

设计飞轮电机时，选择相对多的极对数.由式(4)可知，力矩波动的频率与飞轮电机的磁钢极对数成正比，适当提高电机的极对数有利于提高力矩波动的频率，可降低力矩波动的影响.

从飞轮电机磁场分布及绕组设计入手，改善电机的反电势波形，使其平顶宽度尽量大，以降低力矩波动系数.通常认为将磁钢径向充磁后会获得较平坦的气隙磁场分布，但磁钢极矩较小且磁路气隙较大时，径向充磁的优势将不再明显，同时径向充磁较难实现，所以可采用多块平行充磁的磁钢拼接方法来改善气隙磁场的分布，获得较平的反电势波形以降低力矩波动.

根据反电势的波形，在绕组电流中注入谐波，改善绕组电流波形，从而降低力矩波动.

4.2 力矩跳动的抑制

力矩跳动由驱动方案误差造成，其抑制方法主要集中在控制电路及控制方法的设计上.目前控制电路主要有三相半桥型、三相全桥型、三相H桥型驱动电路，常用的控制方法有PWM控制、PWM/PAM控制，常用的制动方法有能耗制动、反接制动和反接制动与能耗制动共用等制动方式，其中利用飞轮动能的释放产生反向电磁力矩实现制动控制的方式为能耗制动方式;通过电源反接或者改变换向时序获得与电源反接相同结果的控制方式为反接制动方式.

目前比较常用的是基于三相半桥型驱动电路，采用PWM/PAM控制方法，制动时仅有反接制动的驱动方案，其主要缺点是反作用飞轮转速过零时存在必然的力矩跳动，若将其制动方案转变为能耗制动和反接制动联合的制动方案［10］，则可克服转速过零的力矩跳动.

5 结论

1)反作用飞轮中存在多种非理想力矩，其中力矩波动和力矩跳动属于电磁力矩范畴，称其为非理想电磁力矩.

2)力矩波动由飞轮电机的非理想反电势产生.力矩波动大小与反电势波形有关，力矩波动频率与飞轮转速成正比.力矩波动的存在使卫星姿态发生同频率波动，低频力矩波动较高频力矩波动对卫星姿态的影响大，尤其在飞轮转速过零时力矩波动的影响最大.

3)力矩跳动是飞轮驱动器的控制误差引起的，发生在飞轮电机的状态切换时刻.力矩跳动的存在使卫星姿态发生偏差，最大偏差随力矩跳动幅值和力矩跳动持续时间的增加而增加.

4)当卫星姿态控制精度要求较高时，力矩波动和力矩跳动的影响不容忽视，可根据两种力矩的产生机理，选择相应的抑制措施.

［1］NUDEHI S S，FAROOQ U，et al.Satellite attitude control using three reaction wheels［C］//2008 American Control Conference.Washington:［s.n.］，2008:4850-4855.

［2］MASTERSON R A，MILLER D W，GROGAN R L.Development and validation of reaction wheel disturbance models:empirical model［J］.Journal of Sound and Vibration，2002，249(3):575-598.

［3］ZHAO Yang，SUN Fei，TIAN Hao.Development of methods identifying parameters in reaction wheel assembly disturbance model［J］.Aircraft Engineering and Aerospace Technology，2006，78(4):326-330.

［4］ERIC S，BILL B.Behavior of reaction wheels near zero speed［C］//27thAnnual AAS Rocky Mountain Guidance and Control Conference.United states:Univelt Inc，2004:361-372.

［5］BILL B.High fidelity mathematical modeling of reaction wheel performance［C］//Proceedings of the 1998 Annual AAS Rocky Mountain Guidance and Control Conference.United states:［s.n.］，1998:483-496.

［6］郭永东，卢靖华.飞轮制动切换研究［J］.微特电机，1995(3):1-5.

［7］杜坤梅，李铁才.惯性飞轮电机力矩伺服控制系统［J］.电机与控制学报，2001，5(2):119-121.

［8］章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学，1998:147-155.

［9］张利宾.基于磁控和轮控的微小卫星姿态控制算法研究［D］.哈尔滨:哈尔滨工业大学，2007.

［10］ZOU Jibin，CHEN Xia，TANG Yu.A novel torque servo control system for the flywheel motor［C］//Proceedings of the 11thInternational Conference on Electrical Machines and Systems.Wuhan，China:［s.n.］，2008: 1488-1490.