一种改进的数字混沌编码器
2011-03-08肖利丽何世彪吴永彬
肖利丽,何世彪,田 东,吴永彬
(重庆通信学院,重庆 400035)
1 引 言
随着知识经济、信息产业的发展,信息安全问题日益突出,受到社会的广泛关注。对信息安全新理论与技术的研究已经成为高新技术发展中一个重要的热点问题。近年来,混沌方法在保密通信中的应用受到越来越多的关注,将混沌方法应用于保密通信最初是由Tang等人提出的[1]。Tang在文章中指出:一个混沌电路可以通过输入信号同步驱动。后来,Chua和Newcomb[2-5]等人对混沌电路的同步进行了研究,他们一致确认了混沌用于保密通信的可能性。
混沌信号的隐蔽性、不可预测性、高度复杂性和易于实现等特性特别适合于保密通信[11-13]。Frey提出的数字混沌保密通信方案结构简单,易于实现。但是在一些要求较高的保密通信环境下,这种简单的方法明显存在不足。为了提高通信保密性能,本文对Frey原有结构进行了改进。
2 数字滤波器的混沌现象
在构造一个实际的离散混沌系统时,首先遇到的问题是“字长效应”(或“有限精度”)的影响。Chua和Lin[4-6]曾对有限字长效应的非线性递归数字滤波器进行了研究,其中数字滤波器如图1所示,其有限字长效应由一个非线性函数 fL(·)表示,如图2所示。研究和仿真实验显示,由于有限字长效应的存在,非线性数字递归滤波器在一定初始条件和参数下会呈现混沌行为。图1中,x(n)和 y(n)分别为滤波器的输入和输出,z-1为延时器,a、b为滤波器参数。
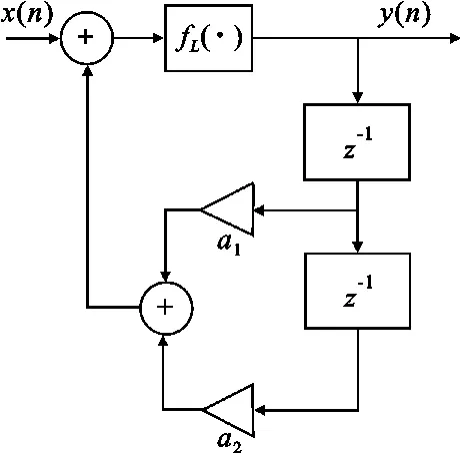
图1 一个二阶数字滤波器Fig.1 A second-order digital filter
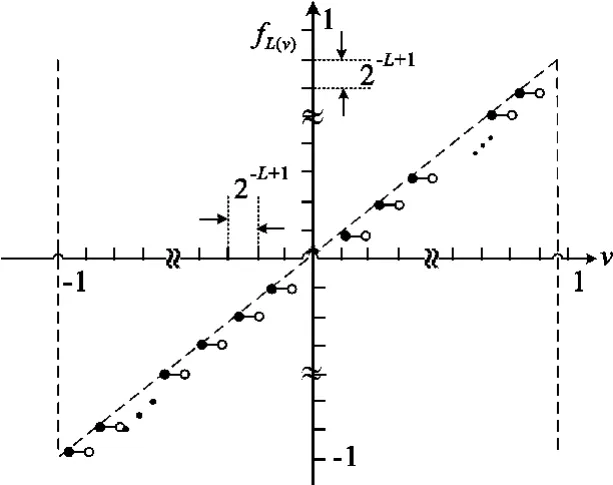
图2 有限字长效应的非线性函数特性Fig.2 Characteristic of nonlinear function with the finite word length effect
利用数字滤波器产生混沌现象面临的一个重要问题是对混沌映射的参数和状态只能用有限的精度来表示,这使得一个理论上的混沌系统实际上总可以表达成一个有限状态机,并且该系统具有有限的周期。随着字长的增加,非线性滤波器的周期将会迅速增长,同时,非性线数字滤波器的混沌行为基本上被保存了下来,这种情况被称为准混沌(Quasi-Chaotic,QC)现象,如图3所示。Frey[7,8]在 Chua等人工作基础上,给出了准混沌应满足的一组特性,并将它作为数字混沌滤波器是否产生混沌的检验标准。这组特性包括:
(1)对几乎所有初始条件,零输入具有宽带噪声谱的响应,并且在相同的初始条件下,该响应的自相关函数与不相关的噪声相似;
(2)对几乎所有初始条件,任意输入通过滤波器都具有宽带噪声谱的响应,并且在相同的初始条件下,该响应的自相关函数与不相关的噪声序列相似;
(3)对几乎所有初始条件,任意输入通过滤波器所产生的响应与其输入是不相关的;
(4)对不相同的初始条件,相同输入通过滤波器所产生的响应之间是不相关的;
(5)对两个结构相同的滤波器,即使它们具有非常接近的初始状态,任意相同的输入总会使两个滤波器中的状态分离。
满足这组特性要求的数字滤波器可以认为具有一定的混沌特性,能够产生准混沌现象,可以用于混沌编码或其它保密通信。
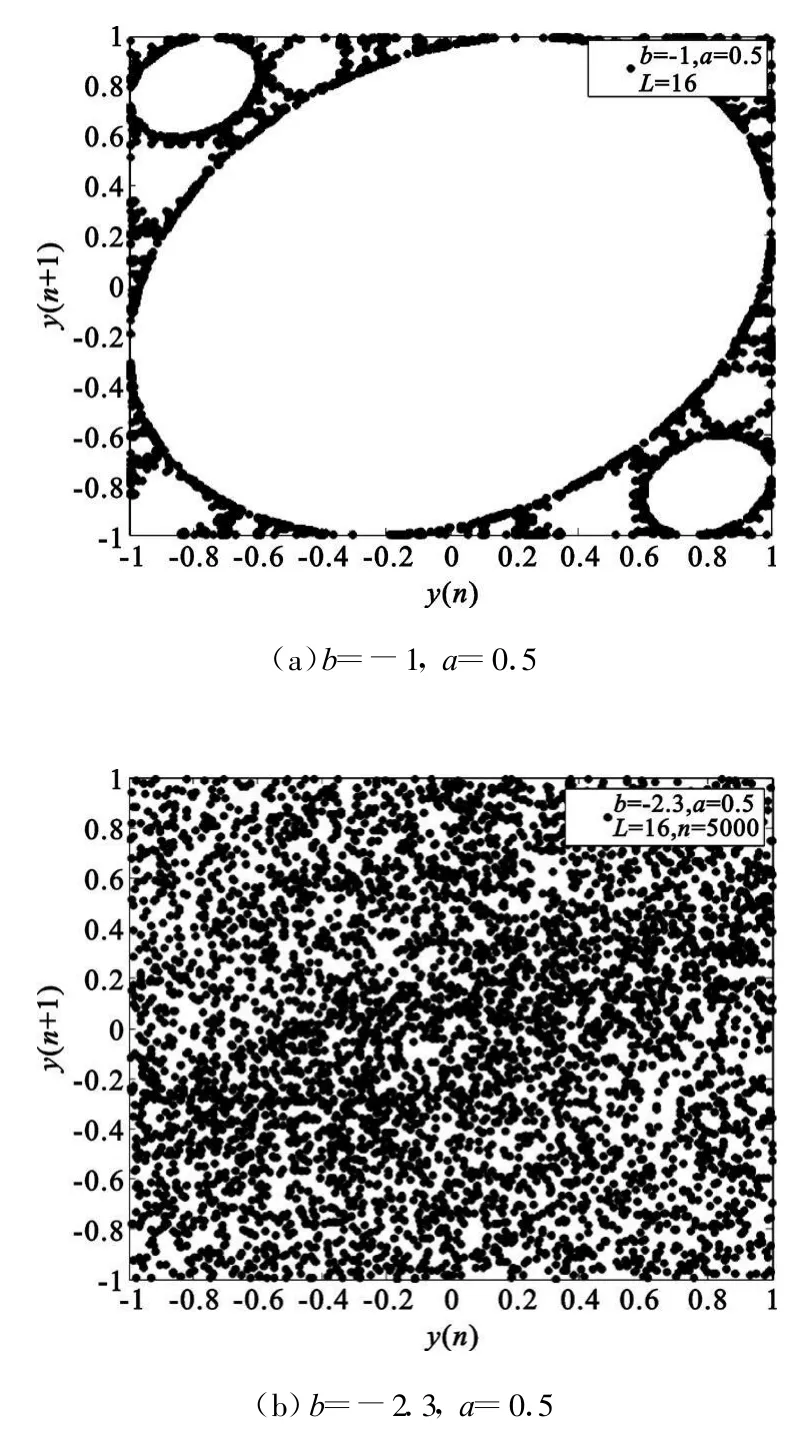
图3 非线性数字滤波器的混沌特性Fig.3 Chaotic characteristic of nonlinear digital filter
3 混沌编码器结构和性能分析
3.1 基于非线性数字滤波器的混沌编解码器
根据文献[7]给出的非线性递归数字混沌编码器的原理和一般性方程,数字混沌编码器的编码过程可以表示为
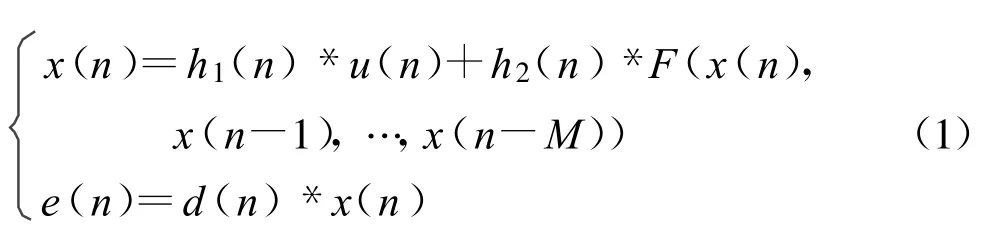
式中,u(n)为信息信号,F(·)为非线性映射函数,+、*分别为加法和卷积运算,在有限精度的硬件实现中,也可认为是一种广义的非线性运算;x(n)为内部状态,h1(n)和h2(n)是IIR或FIR滤波器的脉冲响应,e(n)为加密后的序列,被传送到接收端。混沌加密的过程就是经过由式(1)构成的非线性递归滤波器系统,将信息信号u(n)变换为类似白噪声的混沌信号e(n)。
解码时,采用与式(1)相对应的逆系统来对e(n)进行直接逆滤波。解码过程为
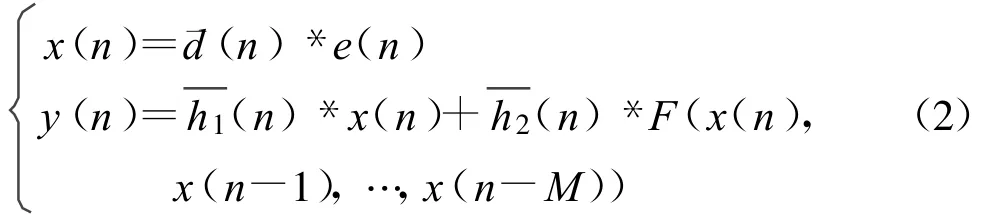
图4就是满足式(1)和式(2)的一个简单的编解码器结构,其编解码方程为
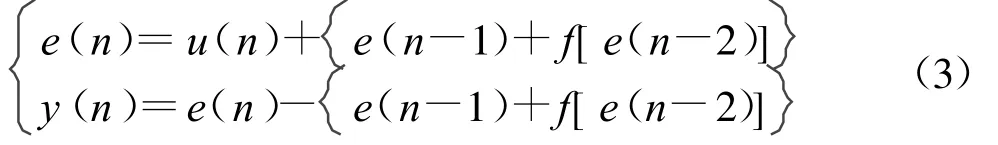

图4 基于非线性数字滤波器的混沌编解码器Fig.4 Chaotic digital en-decoder based on nonlinear digital filter
图4中左循环移位函数(LCIRC)为 F(·),即乘以2并加进位项;所有加、减都以模2m进行运算(m为字长)。下面对该结构生成的编码信号进行性能分析。
假设输入信号 u(t)=5sin(nπ/25),初始条件e(-1)=0,e(-2)=1000,a1=1,a2=1,字长 L=16,仿真点数为1000点。我们可以得到编码器的加密序列、编码信号的相图、自相关函数和互相关函数分别如图 5(a)、(b)、(c)、(d)所示。
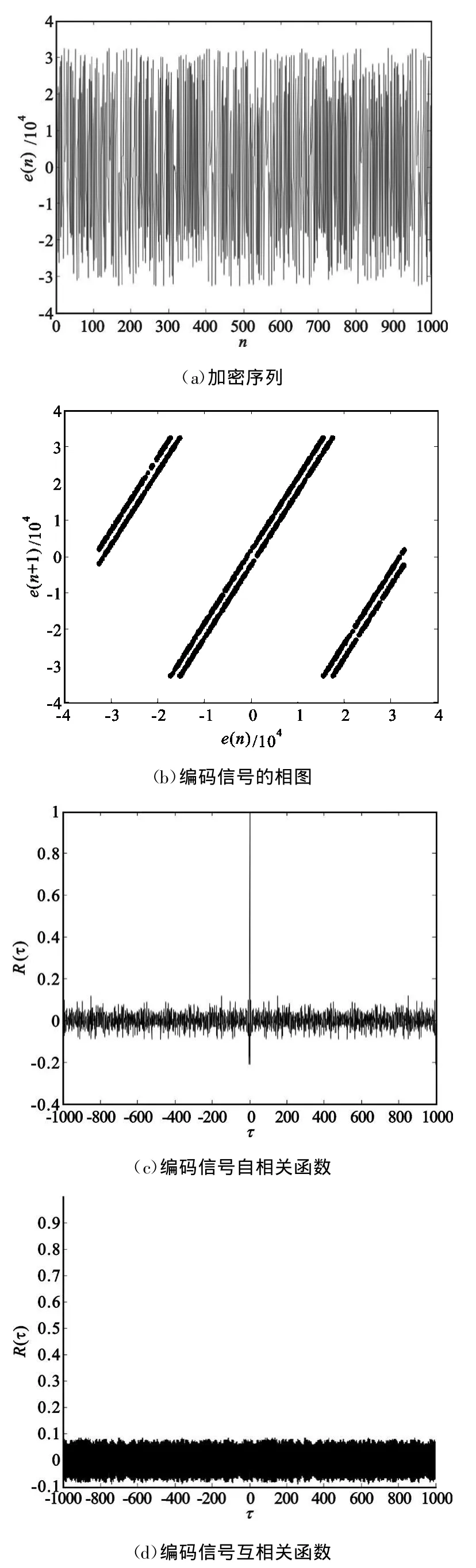
图5 编码信号的特性Fig.5 Characteristic of encoded signal
Frey用频谱、自相关函数和互相关函数等方法深入研究了这一类结构的数字滤波器后指出:该类编码器明显具有QC特性,适用于保密通信的需要。并且由于解码器是FIR滤波器,所以突发错误不会传播。编码输出传送过程中的一个误码,在解码器端只会引起3个突发误码,所以不管起始状态如何,解码器总能锁定到e(n)上,也就是说,即使解码器没有被初始化,经过一个较短的突发误码后,解码器也能精确地恢复出输入序列u(n),如图6所示。
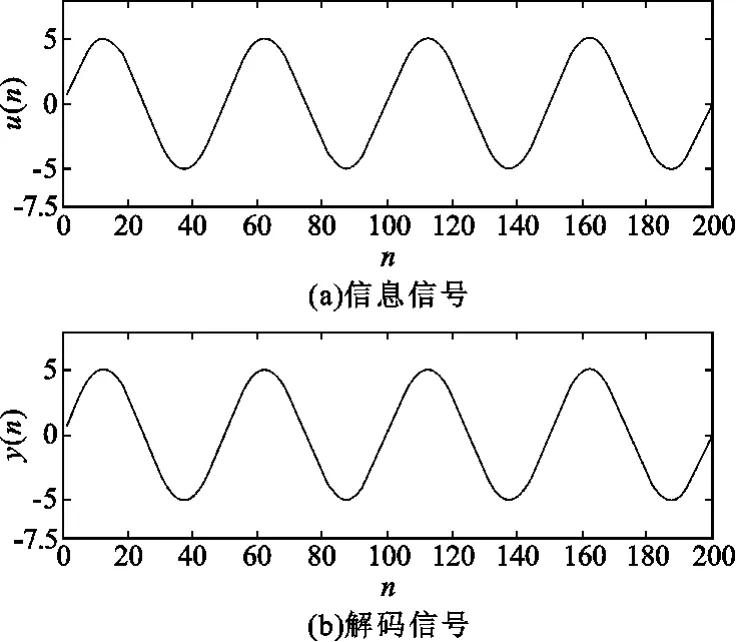
图6 解码信号与信息信号的比较Fig.6 Comparison between decoded and original signal
3.2 改进后的数字混沌编解码器
上述数字混沌保密通信方案结构简单,易于实现。但是在一些要求较高的保密通信环境下,这种简单的方法明显存在不足[7-10]。由于解码器在解码前不需要初始化,因此攻击者利用这一特点可以有效地重构出解码器的结构。针对这一缺陷,对上述编-解码结构进行了改进,如图7所示。改进后的解码器输出y(n)不仅与输入e(n)有关,而且还与初始状态有关。下面对改进的数字混沌编码器的性能加以分析,并与原有结构编码器性能进行比较,仿真条件与上述相同。
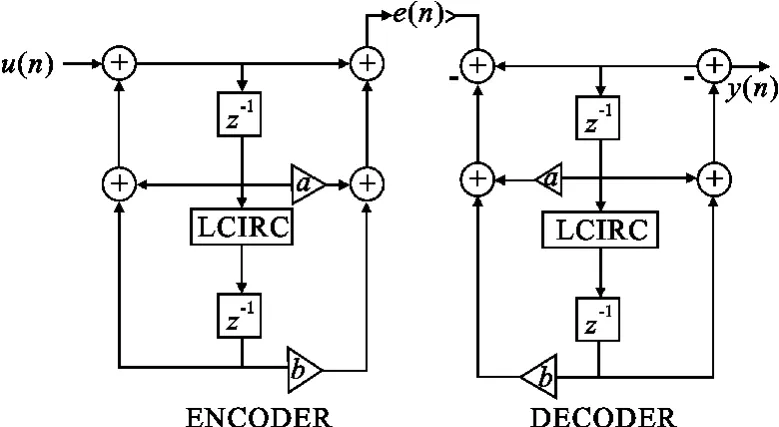
图7 改进的编解码器Fig.7 Enhanced encoder and decoder
3.2.1 自相关特性
对于一个性能良好的加密系统,其输出的编码信号应该具有δ-like自相关特性,而且编码信号与原始信号的互相关应接近0。图8显示了在相同输入下原有结构和改进结构的归一化自相关函数比较结果,从图中可以看出,改进结构编码信号的自相关特性优于原有结构。
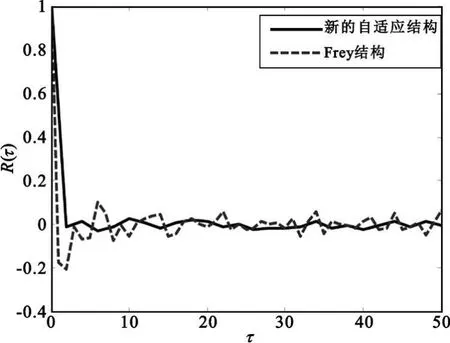
图8 自相关函数比较Fig.8 Comparison of autocorrelation function of the encoded sequence
3.2.2 互相关特性
两种结构的编码信号互相关函数比较结果如图9所示,从图中可以看出,两者的互相关函数都非常接近于0。从图8和图9我们可以知道,改进结构具有更类似噪声的相关特性,更利于保密通信的应用。

图9 互相关函数比较Fig.9 Comparison of crosscorrelation function of the encoded sequence
3.2.3 编码器对参数的敏感性
图10显示了在解码器初始状态失配时两种结构的解码结果。从图中我们可以看出,原有结构在一小段时间后确实恢复出了原始的信号,而改进结构却得到了完全不同于原始信号的杂乱的解码信号,这说明改进结构的数字混沌编码器具有更高的安全性。
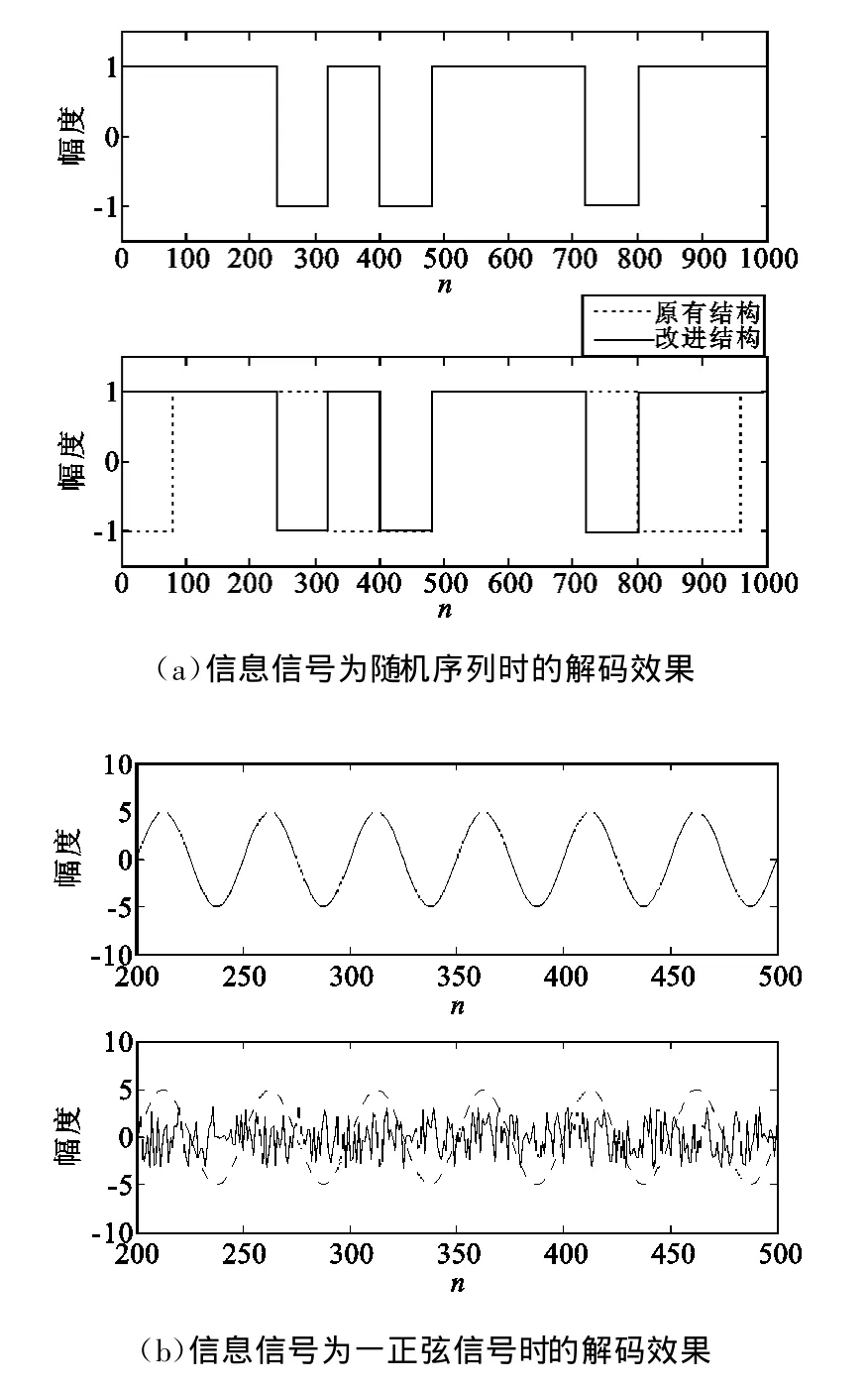
图10 初值不匹配时的解码结果Fig.10 Decoding result with no-match of initial value
仿真结果表明,只有当编、解码器的初始状态相同时,解码器才能正确地恢复出信息序列。可以看出,改进后的加密、解密结构比原结构的保密性能更好。
4 结 论
本文首先介绍了数字滤波器中的混沌现象,然后研究了Frey建议的数字混沌编码器。在分析Frey编码器不足的基础上,提出了改进的数字混沌编码器。仿真实验表明,通过调整解码器的初始状态,只有当解码器的初始条件和编码器的相同时,才能进行正确地解码,使编码器具有更高的保密性。因此,改进后的编码器具有更好的保密性能,更适用于保密通信。但是在加入噪声信号的情况下,数字混沌编码器的解码效果非常不理想,从仿真实验中得到,只有在噪声极其小的情况下方可正确译码。下一步主要就是针对大噪声情况下的解码效果进行研究。
[1]T angY S,Chua L O.Synchronization and Chaos[J].IEEE T ransactions on Circuits and Systems,1983,30(9):620-626.
[2]李辉.混沌数字通信[M].北京:清华大学出版社,2006:93-94.LI Hui.Chaos digital communication[M].Beijing:Tsinghua University Press,2006:93-94.(in Chinese)
[3]Newcomb R W.Chaotic generation using binary hysteresis[J].CircuitsSystem andSignalProcessing,1986,5(3):321-341.
[4]Chua L O.Chaos and fractalsfrom third-order digital filters[J].International Journal of Circuit Theory Applications,1990,10(18):245-255.
[5]Chua L O.Chaos in digital filters[J].IEEE Transactions on Circuits and Systems,1988,35(6):648-658.
[6]Lin T,Chua L O.On chaos of digital filters in the realworld[J].IEEE Transactions on Circuits and Systems,1991,38(5):557-558.
[7]Frey D R.Chaotic Digital Encoding:AnApproach to Secure Communication[J].IEEE Transactions on Circuits and Systems,1993,40(10):660-666.
[8]Frey D.On adaptive chaotic enclding[J].IEEETransactions on Circuits and Systems,1998,45(11):1200-1205.
[9]Zhang J G,Dai X C,Xu P X.Improvement to Frey′sAdaptive Chaotic Encoder[C]//Proceedings of the 3rd World Congress on Intelligent Control and Automation.Hefei,China:IEEE,2000:2479-2483.
[10]袁新峰.刘嘉勇.一种混沌密码序列的产生及其改进[J].电讯技术,2003,43(2):87-90.YUAN Xin-feng,LIU Jia-yong.Generation and Improvement of a Chaotic Cipher Sequence[J].Telecommunication Engineering,2003,43(2):87-90.(in Chinese)
[11]王亚东,张辉,高帆.混沌跳频序列的设计及其性能检验[J].电子元器件应用,2007,9(3):59-62.WANG Ya-dong,ZHANG Hui,GAO Fan.Design and Performance examination of Chaotic Hopping Sequence[J].Electronic Component&Device Applications,2007,9(3):59-62.(in Chinese)
[12]蒋国平,万冬东,薛龙.超宽带通信中一种新的伪混沌编码器及其解码方法[J].通信学报,2005,26(10):72-76.JIANG Guo-ping,WAN Dong-dong,XUE Long.New realization scheme of pseudo-chaotic-based encoder and decoder for UWB communications[J].Journal on Communications,2005,26(10):72-76.(in Chinese)
[13]覃玉祝,谢进.用MATLAB进行混沌动力系统的分析[J].机械设计与制造,2010,7(7):73-75.QIN Yu-zhu,XIE Jin.Analyse dynamic systems of chaos with MATLAB[J].Machinery Design&Manufacture,2010,7(7):73-75.(in Chinese)
