轨道动力学模型与数值方法研究进展

雷晓燕

（华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013）

轨道动力学模型与数值方法研究进展

雷晓燕

（华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013）

随着列车速度的提高和轴重的增加，车辆与轨道之间的相互作用更加激烈。深入开展轮轨动态作用机理研究，对高速重载铁路安全平稳运行具有重要意义。文章回顾了轨道动力学模型的研究进展，重点介绍了五种轨道动力学模型及算法，即车辆－轨道－路基非线性耦合系统交叉迭代算法，新型车辆单元和轨道单元模型，列车轨道系统动态分析的移动单元法，移动荷载作用下轨道动力学分析的多层梁模型，及轨道－路基－大地系统动态响应分析的有限元与边界元耦合法，并讨论了各种方法的优缺点。这些模型和算法是研究轨道动力学问题的重要基础和工具。为了提高计算精度和计算效率，根据分析问题的特点可以选择不同的模型和算法。

轨道动力学；交叉迭代法；车辆单元；轨道单元；移动单元法；有限元与边界元耦合法

随着列车速度的提高，轴重的增加，行车密度的加密以及新型车辆和新型轨道结构的大量工程应用，使车辆与轨道间的相互作用更加复杂，动应力增大，影响列车运行的安全与稳定。列车作用在轨道上的动荷载可分为三类：移动的轴荷载、固定作用点的动荷载、移动的动荷载。轴荷载的作用与车辆动力学无关，其大小不变，但由于其作用点是移动的，故对轨道－路基－大地系统的作用为动荷载作用。当移动轴荷载的速度接近轨道的临界速度时，轨道将产生剧烈振动。固定作用点的动荷载来自车辆通过固定不平顺（如钢轨接头、无缝钢轨焊缝及道岔岔心）引起的撞击。移动动荷载则由轮轨接触表面的不平顺而产生。进行列车－轨道系统动力学分析是研究复杂轮轨关系和相互作用机制的基础，也是指导和优化车辆、轨道结构设计必不可少的内容。

1 轨道动力学模型与数值方法研究回顾

国内外学者在该领域做了许多工作，并取得了一定的研究成果。轨道动力学模型与数值方法的研究经历了一个从简单到复杂的发展过程，从历史上看，移动载荷/车辆结构是结构动力学尤其是列车轨道系统中最早的实际问题之一。Knothe和Grassie等[1-3]系统地介绍了频域内轨道动力学和车辆－轨道相互作用的研究进展。Mathews[4-5]采用傅里叶变换的方法（FTM）和移动的坐标系统，解决了任意移动荷载作用在弹性基础无限长梁上的动力问题。傅里叶变换方法属于频域分析法。运用傅里叶变换的方法Trochanis[6]，Ono和Yamada[7]也做了一些类似的研究工作。Jezequel[8]将轨道结构简化为弹性基础上无限长的欧拉－伯努利梁，考虑其转动和横向剪切效应，列车荷载为匀速运动的集中力。Timoshenko[9]通过模态叠加，在时域内解决了移动荷载作用于简支梁上的控制微分方程的求解。Warburton[10]用解析的方法分析了相同的问题，并且发现了移动荷载在特定的速度下梁的挠曲量将达到最大。Cai等[11]运用模态叠加法研究了移动荷载作用于周期滚动支座上无限长梁的动力响应问题。

以上工作都是将轨道梁视为连续体，并且用解析法求解控制微分方程。这些方法虽然简单，但不适合考虑整车多自由度的车辆轨道系统，因而在车辆轨道动力学中的作用是有限的。近年来，有限元法在实际工程中的应用越来越广泛。有限元法是通过将轨道离散为有限个单元、假设位移函数得到单元矩阵，从而形成有限元求解方程。Filho[12]综述了用有限元法求解移动荷载作用于均质梁上的动力分析方法。有限元法是一种流行的解决车辆轨道动力学问题的方法。Olsson[13]采用有限元法，考虑了不同的车辆模型，不同的振动模态和表面不平顺的影响，用板柱单元模拟桥梁振动的问题。Fryba等[14]提出了适合匀速移动荷载作用于弹性基础梁的随机有限元分析法。Thambiratnam和Zhuge[15-16]建立了任意长度的弹性基础简支梁分析的有限元模型。Nielsen和Igeland[17]建立了包含转向架、钢轨、轨枕和路基为一体的有限元模型，运用复模态叠加技术分析了轨道磨耗、车轮扁平和轨枕悬空等因素的影响。Zheng和Fan[18]研究了列车－轨道系统的稳定性问题。Koh等[19]提出了新型移动单元法，这种单元是建立在一个随列车一起运动的相对坐标系上，而普通的有限元法是建立在固定的坐标系中。Auersch[20]在三维空间建立了用有限元和边界元联合求解法分析有砟、无砟垫的轨道结构模型，并对道砟垫的刚度、车辆簧下质量、轨道质量和路基刚度等进行了参数分析。Clouteau等[21]基于有限元－边界元耦合法提出了分析地铁振动的有效算法，该算法的核心是运用Floque变化以考虑沿隧道方向轨道的周期性。Andersen和Jones[22-23]运用耦合的有限元－边界元法研究并比较了二维与三维模型的差异，他们工作的一个重要发现就是二维模型适合于定性分析，且能快速得到分析结果。Thomas[24]建立了多刚体车辆－轨道模型研究侧风对高速列车在曲线地段蛇形运动的作用，分析了侧风强度、车辆参数对列车动力响应的影响。Ganesh Babu等[25]运用有限元法，考虑路基、道砟和钢轨垫板等参数的变化，对预应力混凝土轨枕和木枕轨道结构的轨道模量进行了分析。Cai[26]将大地处理成多孔弹性半无限域介质，基于Biot多孔弹性动力学理论，研究了列车通过时轮轨相互作用对大地环境振动的影响。

自上世纪90年代初起，国内众多铁路科研人员陆续开展了车辆－轨道耦合动力学领域的理论与应用研究。翟碗明[27-28]就车辆－轨道耦合动力学原理开展研究[27]。2002年翟碗明发表了一篇《车辆－轨道耦合动力学研究的新进展》一文[29]，回顾了车辆－轨道耦合动力学的研究历史，并对国内外研究进展作了概要介绍。雷晓燕[30-32]带领的课题组也较早地开展了轨道动力学模型与数值方法研究，于1998年出版了《轨道结构数值分析方法》专著，系统介绍了单轮附有簧上质量轨道模型，半车和整车附有二系弹簧质量轨道模型，及求解轨道结构振动方程的数值方法[33]。国内在本研究领域的研究工作还有：徐志胜等[34-35]运用车辆－轨道耦合动力学理论，编制了基于Timoshenko梁钢轨模型的车辆－轨道耦合振动分析软件，分析了车辆－轨道系统的垂向振动特性，并与基于Euler梁模型的软件的仿真结果进行了比较分析。结果表明：两者的仿真结果基本一致，但在较高频域，两种分析方法得到的固有频率差异较大，Timoshenko梁模型能更好地反映轮轨系统的高频特性。谢伟平、镇斌[36]运用傅里叶变换和留数理论得到了变速移动荷载下无限长Winkler梁稳态动力响应的解析表达式，与Kenney的经典解求解过程相比，文中给出的求解过程具有更加明确的物理意义。罗雁云等[37]通过建立无缝线路有限元动力分析模型，研究了钢轨自振频率和温度力之间的关系。该动力模型包括钢轨、扣件和轨枕，考虑了钢轨断面特性、钢轨磨耗、轨下刚度以及扣件的弹性刚度和扭转刚度等因素对动力模型计算的影响，计算结果表明该模型可以更准确地分析无缝线路轨道结构中钢轨纵向力与振动特性的内在联系。魏庆朝等[38]建立了直线电机地铁系统横、垂向车辆－轨道耦合动力学仿真模型，计算了不同的轨道结构形式（长枕埋入式与板式）和不同板下支承刚度和阻尼情形下，直线电机车辆与轨道结构的动力响应，并进行了对比分析。结果表明：长枕埋入式轨道结构的车体垂向加速度略大于板式轨道，而板式轨道的钢轨横向加速度以及钢轨垂向位移则要略大于长枕埋入式，板下阻尼值的增大有利于轨道板减振，板下刚度对轮轨力、钢轨位移和电机气隙影响较小，当板下刚度增加时，轨道板的位移值变小但轨道板的加速度值变大。高亮等[39]根据道岔、桥梁结构和布置形式，建立了桥上无缝道岔空间耦合模型，从温度荷载、竖向荷载、钢轨横向变形等方面对空间力学特性进行了分析。冯青松等[40]采用傅里叶变换和传递矩阵的方法推导了有砟轨道－路基－地基系统在轮轨接触点处的柔度矩阵，建立了考虑轨道不平顺的车辆－有砟轨道－路基－层状地基垂向耦合振动解析模型，分析了单台TGV高速动车引起路堤本体－地基系统的振动，研究了列车速度、轨道不平顺、基床刚度和路堤土体刚度对路堤本体振动的影响。研究结果表明：路堤本体垂向位移主要由移动的列车轴荷载引起；随着列车速度的提高，路堤振动的“波动性”明显增加；基床刚度和路堤土体刚度对路堤振动影响显著。边学成、陈云敏[41-42]采用动力子结构法研究了移动荷载作用下轨道与层状大地的耦合振动，模型中考虑了轨枕的离散支承影响，后来又采用分层传递矩阵方法研究了大地振动问题[43]。谢伟平[44-45]、聂志红[46]、雷晓燕[47-50]、和振兴[51]、李志毅[52]等也都采用解析的波数－频域法建立了轨道结构单层或多层梁模型，分析了高速列车引起的轨道和大地振动。研究表明：列车速度越高，轨道和大地的振动响应越大；当列车速度低于、接近和高于大地中表面波波速时，大地振动呈现出不同的特性；当列车速度达到某种临界速度时，将引起轨道和大地的强烈振动，当高速列车通过软土地基线路时可能发生这种强振动现象。台湾大学的吴演声、杨永斌[53]提出半解析模型分析高架铁路移动荷载引起的大地振动，由移动轴荷载作用下的弹性支承梁模型求得列车引起的桥墩顶支反力，通过集总参数模型求出桥墩基础与周围土层间的相互作用力；由此作用力求出弹性半空间大地的振动水平。北京交通大学夏禾、曹艳梅等[54]利用解析的波数－频域法建立了列车－轨道－大地耦合模型，将轨道－大地系统考虑为三维层状大地上周期性支撑的欧拉梁模型，也分析了移动列车轴荷载和轨道不平顺引起的动态轮轨力作用下大地的振动响应。

刘学毅等[55]认为，许多情况下轮轨振动表现为耦合性较强的空间振动，因而有必要发展轮轨系统空间耦合振动模型。李德建和曾庆元[56]采用车辆－轨道耦合动力学的方法，建立了车辆－直线轨道空间耦合振动分析模型，其特点在于将轨道离散成30个自由度的空间轨道单元段，并采用构架人工蛇行波作为激振源。梁波[57]和苏谦[58]详细考虑了路基结构的参振作用，开展了车辆－轨道－路基垂向耦合动力学研究。王其昌[59]、罗强[60-61]运用文献[27-28]的车辆－轨道垂向统一模型，分别研究了高速、提速或快速铁路列车通过路基－桥梁过渡段时的动力学问题，为高速铁路路桥过渡段的路基加固、变形控制及过渡段合理长度的确定等提供了理论依据。王平[62]和任尊松[63]采用车辆－轨道耦合动力学理论分别开展了车辆与道岔相互作用研究，并应用于我国提速道岔动力分析，对我国铁路提速中道岔的改进设计具有重要意义。

列车对轨道的动力作用是一个随机过程，对车辆－轨道系统进行随机振动分析能够更全面地了解轮轨作用机制。研究车辆－轨道耦合随机振动一般采用两种激励模型：定点激励模型和动点激励模型。定点激励模型是假设车辆与轨道固定不动，轨道不平顺激励以一定速度向后运动。动点激励模型假设车辆以一定的速度在轨道上运行，其做法是首先根据轨道不平顺功率谱反演出一条轨道不平顺样本，然后利用数值积分方法求解系统的时域响应，最后对时域响应进行傅里叶变换，得到系统响应的功率谱。陈果[64]、雷晓燕[65-66]等曾采用动点激励模型求解车辆－轨道耦合系统的随机振动响应。这种方法可考虑轮轨接触力的非线性，但由于存在积分环节，计算量较大，另外利用轨道谱反演的轨道不平顺的时域样本以及通过时域分析结果进行响应的功率谱估计可能会导致一定的分析误差。Lu等[67]建立了车辆－轨道随机振动分析模型，提出了用虚拟激励法和对偶算法求解的方法，车辆考虑竖向振动和转动效应，共有10个自由度，轨道被模拟成包含钢轨、轨枕和道砟无限长的成周期变化的欧拉梁。假设车辆不动，对轨道施加一激励，考虑轨道表面有一运动的随机不平顺谱，该随机不平顺谱是以列车速度向反方向运动的。

2 车辆－轨道－路基非线性耦合系统交叉迭代算法

建立车辆－轨道－路基非线性耦合系统分析模型如图1所示，将整个耦合系统分为上部车辆系统和下部轨道系统两个子结构[68-69]。在车辆系统模型中，考虑车体和转向架的沉浮振动和点头振动，整车模型有10个自由度，用矩阵形式表示，上部车辆系统振动方程为式中：Mu为车辆的质量矩阵；Cu为车辆的阻尼矩阵；Ku为车辆的刚度矩阵；Qu为车辆的等效荷载向量；au，a˙u和a¨u分别表示车辆的位移、速度和加速度向量。

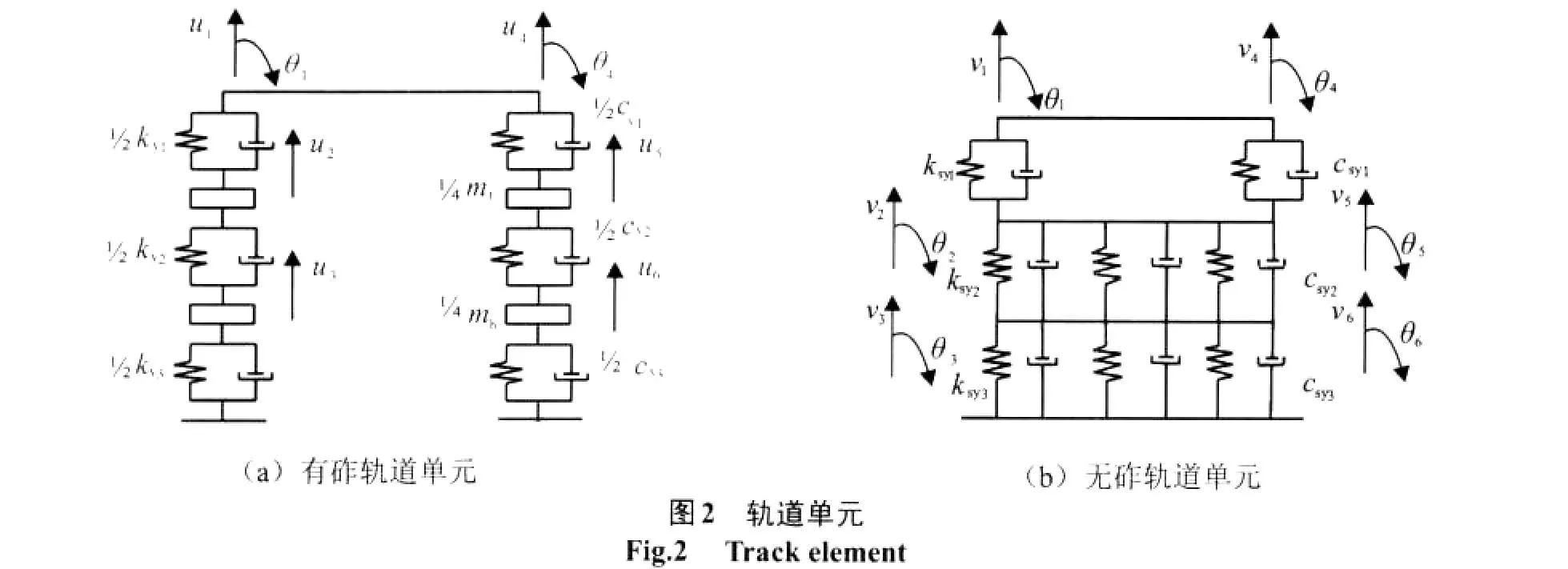
下部轨道结构包括钢轨、弹性扣件、轨枕、道咋和路基，如图2所示，其中，ui，vi（i=1，2，3，…，6）分别表示轨道单元第i个节点的竖向位移；θi（i=1，2，3，…，6）表示第i个节点的转角；ky1，ky2，ky3和cy1，cy2，cy3分别表示有砟轨道扣件、道砟和路基的刚度及阻尼；ksy1，ksy2，ksy3和csy1，csy2，csy3分别表示无砟轨道扣件、CA砂浆和防水层的刚度及阻尼。钢轨被离散为梁单元，轨枕和道咋的质量作为集中质量处理并仅考虑竖向振动效应，扣件和垫层、道咋及路基的弹性及阻尼分别用弹簧和阻尼器表示。轨道结构的有限元方程为

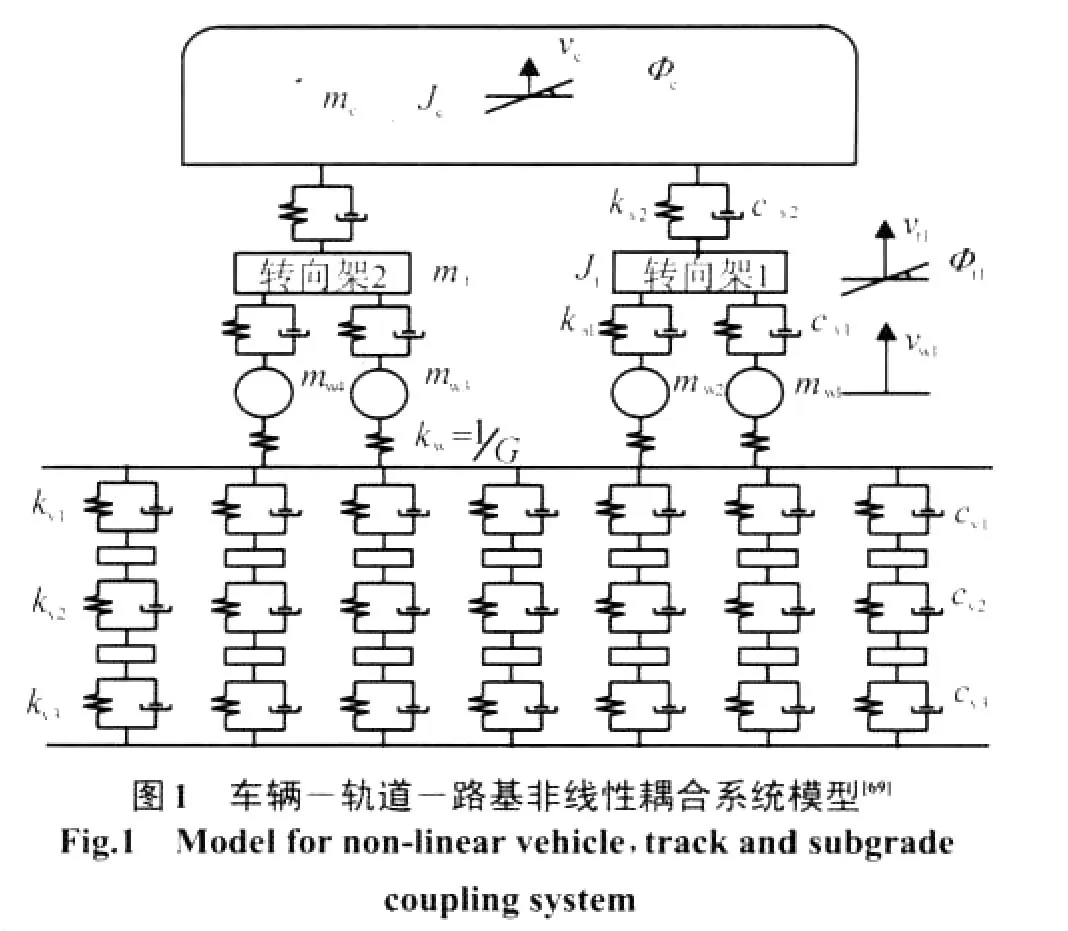
式中：Ml，Cl，Kl，Ql分别是下部轨道结构的质量矩阵、阻尼矩阵、刚度矩阵和等效节点荷载向量；al，a˙l和a¨l分别表示轨道结构的位移、速度和加速度向量。

车辆－轨道－路基非线性耦合系统的动态响应，可运用迭代法对两系统分别交叉迭代独立求解，两系统间通过位移相容和相互作用力的平衡条件联系。有限元动力方程的求解采用Newmark直接积分法，其主要步骤如下[68-69]。

初始计算，在起始第一时间步和首次迭代时，假设轮轨接触力初始值，根据非线性赫兹公式计算轮轨间相对位移。

对时间步长循环：

1）在每一时间迭代步内交叉对下部结构和上部结构求解动力方程，即可得到该时刻结构的动力响应。

2）根据得到的车辆、轨道动力响应，按非线性轮轨接触力公式（3）计算轮轨相互作用力

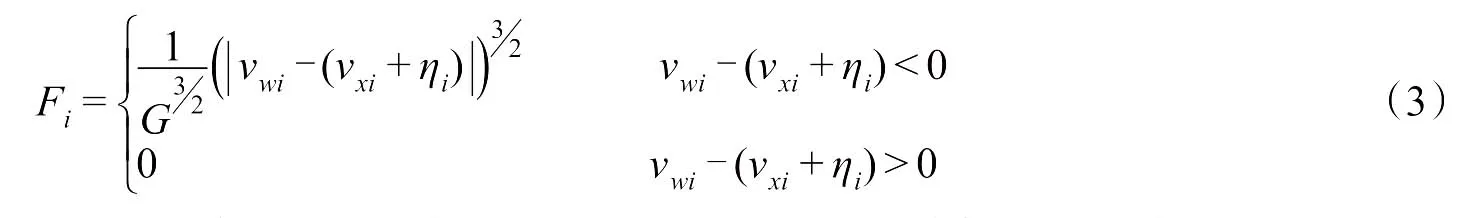
式中：vwi，vxi分别为车轮和钢轨在xi点的位移；ηi为钢轨表面的不平顺；G为轮轨接触挠度系数。

3 车辆单元和轨道单元模型

雷晓燕、张斌[70-72]根据列车－轨道系统运动的特点，提出了适合该问题动力分析的新型车辆单元和轨道单元，运用有限元方法和Lagrange方程，推导了两种单元的刚度矩阵、质量矩阵和阻尼矩阵。运用车辆单元和轨道单元模型，进行了轨道过渡段动力特性有限元分析，对轨道刚度突变、刚度阶梯变化、刚度线性变化和刚度余弦变化四种工况进行了参数分析，得到刚度呈余弦变化的过渡方式引起车辆和轨道的动力响应最小。图3为车辆单元模型[70]，在整车模型中，车体和转向架考虑沉浮振动和点头振动，车轮考虑沉浮振动。该模型共有26个自由度，与传统车辆模型不同之处在于每个车轮下面附有一跨钢轨，钢轨的两个节点考虑竖向位移和转角。附加的钢轨仅用于车辆与轨道之间的耦合，不计其质量和刚度。针对这种新型的车辆单元，建立了将运动的车辆与轨道结构进行耦合的显示算法，从而避免了复杂的程序编制工作。

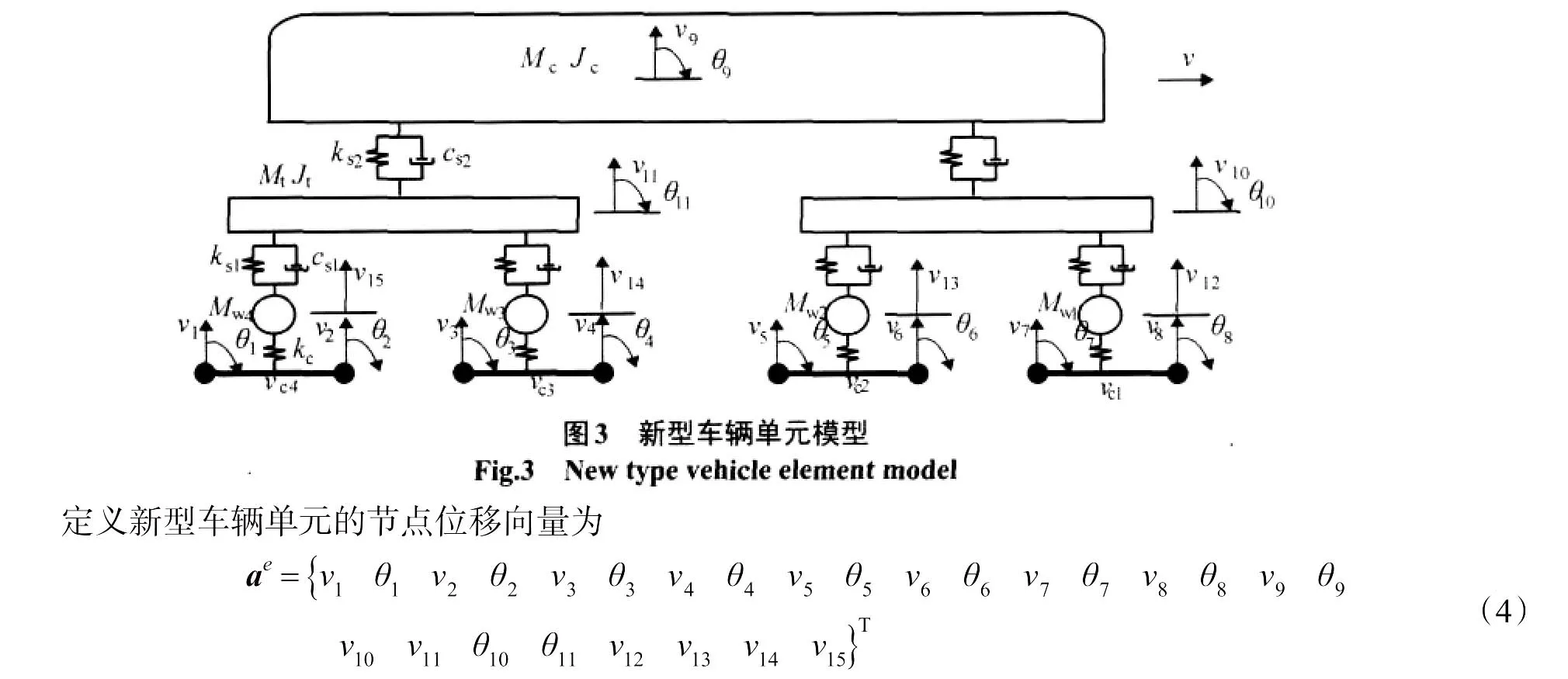
式中：v（ii=1，2，3，…，8）分别表示钢轨第i个节点的竖向位移；θ（ii=1，2，3，…，8）表示钢轨第i个节点的转角；v9，θ9分别表示车体沉浮振动的竖向位移、车体点头振动的角位移；vi，θ（ii=10，11）为前、后转向架沉浮振动的竖向位移、点头振动的角位移；v（ii=12，13，14，15）为第i个车轮的竖向位移；vc（ii=1，2，3，4）为第i个轮轨接触处钢轨的竖向位移。通过列出车辆单元的弹性势能、动能和耗散能可推导出车辆单元的刚度矩阵、质量矩阵和阻尼矩阵。新型车辆单元的有限元方程在形式上同式（1）。轨道单元见图2，其中图2（a）和图2（b）分别为有砟轨道单元和板式无砟轨道单元。

运用新型车辆单元进行仿真分析时，整个列车－轨道系统只需离散成车辆单元和轨道单元，轨道系统离散成轨道单元，一节车辆为一个车辆单元，计算时只需形成一次轨道系统的总刚度矩阵、总质量矩阵和总阻尼矩阵，以后在每一时步的计算中，只需组集车辆单元的刚度、质量和阻尼矩阵，因而极大地提高了计算效率。由于控制方程的建立是基于能量原理，所得到的刚度、质量和阻尼矩阵都是对称的，又由于整个列车－轨道系统只包含车辆和轨道两种单元，使得程序编制特别容易。该方法具有程序编制容易，计算精度高，尤其适合分析整趟列车通过时轨道结构振动的特点。

4 列车轨道系统动态分析的移动单元法

Koh C.G.[19]提出了一种新的有限单元，这种新型单元是建立在一个随列车一起运动的相对坐标系上，而普通的有限元法是建立在固定的坐标系中。这种新型单元被称为移动单元。这种单元不是依附于材料的物理单元，而是一种随着移动列车运动的概念单元。其主要优点是不同于普通有限单元法，这种单元由于随列车一起运动车辆永远不会到达边界；其次，移动车辆不需从一个单元过渡到另一个单元，从而避免了因单元上接触点变化引起力和位移向量的更新；第三，允许不同长度的单元以解决多重接触点（车轮）间不同距离的问题。

图4为车辆轨道模型，车辆简化为移动的轴荷载，假设以匀速V在x方向行驶。钢轨模拟为无限长的欧拉-伯努利梁，钢轨竖向挠度为w，弹性模量为E，截面惯性矩为I，单位长度轨道质量为mr。轨道基础单位长度刚度和阻尼分别为ks和cr，ai为初始时刻第i个车轮距原点的距离。

轨道梁的控制方程为

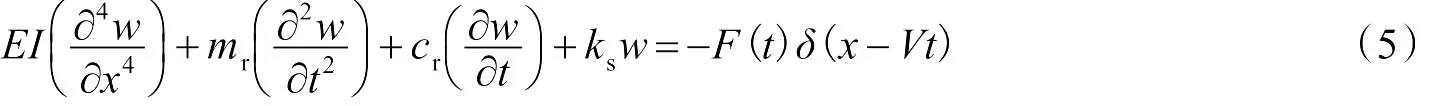
式中：w表示钢轨位移；F表示列车的轴荷载；δ表示狄拉克函数。为方便起见，原点选择在当时间t=0时x=0的接触点处。

图5为用移动单元离散化的轨道梁模型。轨道梁的左右边界都离列车作用点足够的远，从而使得模型边界条件的影响足够的小。考虑一个长度为l，包含节点I和J的典型移动单元，定义移动坐标如下

式中：xI是节点I固定的坐标。相应的，r坐标的原点随移动列车荷载运动。经过简单转化，这个移动单元的控制方程为

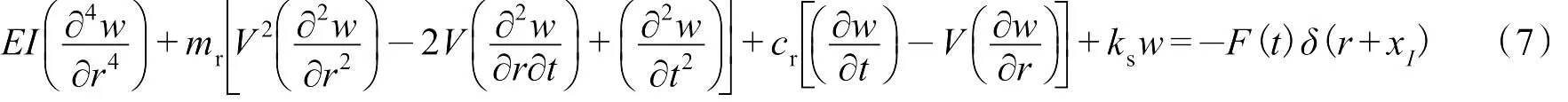
注意到多数单元没有和车辆系统接触，对于这些单元，式（7）右边的力是0。式（7）乘以加权函数w并对单元长度积分，可得到控制方程的弱形式如下

式中：w1，w2和θ1，θ2分别表示单元节点I，J的位移和转角。

单元中任一点的位移可用钢轨两端的位移通过插值表示

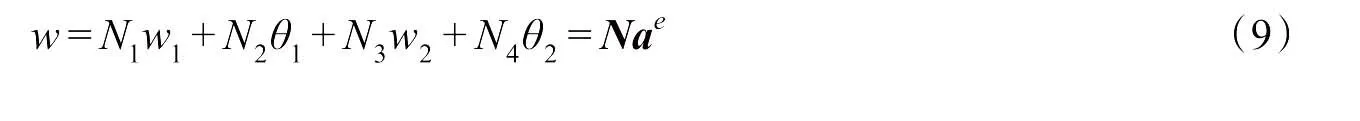
式中：N为位移形函数；ae为单元节点位移向量。

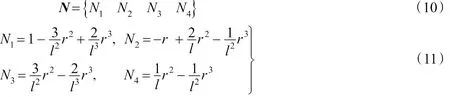
采用Galerkin方法，取加权函数w为插值函数N，并对单元长度积分，可得到单元质量，阻尼和刚度矩阵如下

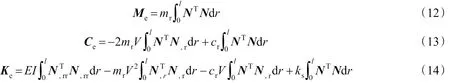
式中：符号（），r表示对r的偏导数。

由单元质量，阻尼和刚度矩阵可以集合得到车辆－轨道系统的总质量、总阻尼和总刚度矩阵，用普通有限元方法即可求得解答。上述方法也适用更复杂的轨道结构模型。

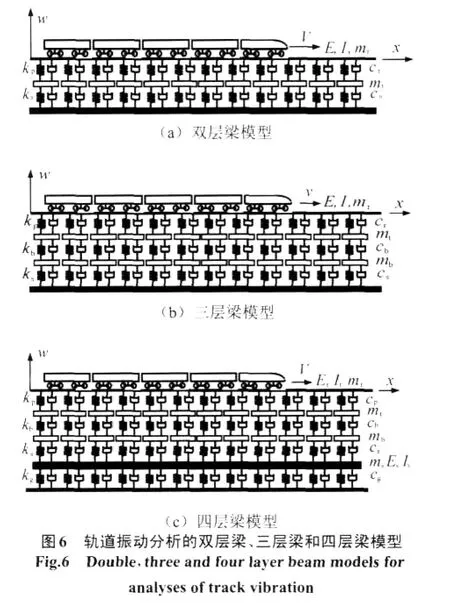
5 移动荷载作用下轨道动力学分析的多层梁模型

根据轨道结构的类型和研究目的可将轨道简化成多层梁模型，如图6所示，图中，w，z，y和g分别为钢轨、轨枕、道床和沥青垫层的挠度；mr，mt，mb和ms分别为单位长度的钢轨质量、轨枕质量、道床质量和沥青垫层的质量；kp，kb，ks和kg分别为单位长度轨下垫板和扣件的刚度、道床刚度、沥青刚度和路基刚度；cr，cb，cs和cg分别为单位长度轨下垫板和扣件的阻尼、道床阻尼、沥青阻尼和路基阻尼。图6（a）为双层梁模型[59]，可用于模拟隧道或桥梁上的无砟轨道结构，图6（b）为三层梁模型[73-74]，适用于有砟轨道，图6（c）为四层梁模型[75]，可用于分析特殊轨道结构，如沥青基础有砟轨道。同样，将列车简化为一列以速度V运动的轴荷载。除此，还考虑轨道表面的随机不平顺。该方法具有计算效率高，尤其适合分析单节和多节组合车辆通过时轨道结构振动的特点。文献[69，73]运用该方法研究了高速列车诱发地面波与轨道强振动机理，分析了高速轨道交通无砟轨道、客货混运铁路专线及沥青轨道基础的振动响应特性和轨道临界速度。

针对轨道结构振动分析的双层梁、三层梁和四层梁模型，列出移动荷载作用下轨道结构的振动微分方程，运用傅里叶变换法，对振动微分方程进行傅里叶变换，求解傅氏变换域中的轨道结构振动方程，得到钢轨、轨枕、道砟和路基位移，再运用快速离散傅里叶逆变换算法，即可求得时域中的钢轨、轨枕、道砟和路基的动力响应。例如，对轨道结构三层梁模型，振动微分方程为

（a）双层梁模型

（b）三层梁模型

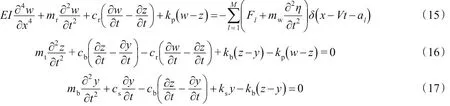
式中：δ为Dirac函数；V为列车运行速度；Fl为第l个轴荷载；mw为轮对质量；al为t=0时第l个车轮距原点的距离；M为轮对总数；η(x=Vt)为轨道随机不平顺值。

车辆－轨道耦合系统的振源考虑了运动的列车轴荷载的影响和由于轨道几何随机不平顺η引起的附加动荷载，后者也是影响轨道结构振动的主要激振源。根据实测得到的轨道几何随机不平顺功率谱密度函数，采用如下三角级数法

式中：Nk为级数求和项数；ηk是平均值为0、标准差为σk的高斯随机变量，对于k=1,2,…,Nk来说，是互相独立的，φk是与ηk独立的，0～2π范围内的同一随机变量，φk本身对于k=1,2,…,Nk来说也是互相独立的；ωk为空间频率。模拟获得轨道几何随机不平顺样本，将轨道不平顺值η代入振动微分方程（15）和轮轨接触力计算公式即可求得轨道结构的振动响应和轮轨接触力[75]。

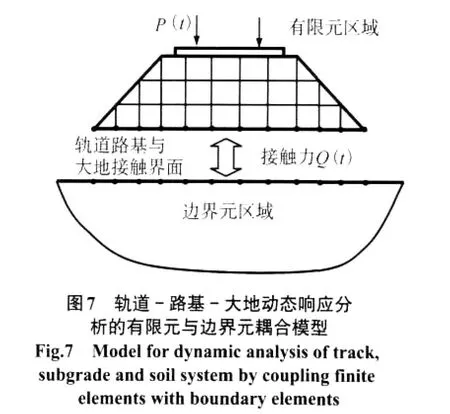
6 轨道－路基－大地系统动态响应分析的有限元与边界元耦合法

上述介绍的模型对路基和大地的处理做了较大的简化，通常简化成弹簧和阻尼器，这与实际情况是有差异的。如需要详细分析轨道－路基－大地系统的动态响应，细化大地结构是必须的。本节介绍用有限元与边界元耦合法分析轨道－路基－大地系统动态响应的有效算法。将轨道－路基－大地系统分成轨道－路基子系统和大地子系统，如图7所示，其中轨道－路基子系统用有限元法求解，大地子系统用边界元法求解，充分发挥有限元法在分析非线性问题和边界元法在处理无限域和半无限域问题的优点，有限元与边界元之间的耦合利用接触界面的位移和接触力的相容条件来实现[76]。

轨道－路基子系统时域中的振动方程为

式中：P(t)为作用在轨道结构上的外荷载；Q(t)为轨道路基与大地之间接触界面的作用力。设作用于轨道结构上的荷载为简谐力P(t)=P^eiωt，则轨道结构的响应亦具有简谐性质，即

7 结论

以上介绍的车辆－轨道－路基非线性耦合系统交叉迭代算法，新型车辆单元和轨道单元模型，列车轨道系统动态分析的移动单元法，移动荷载作用下轨道动力学分析的多层梁模型，及轨道－路基－大地系统动态响应分析的有限元与边界元耦合法，都是研究轨道动力学问题的重要基础和有效数值方法。现将它们的特点总结归纳如下：

1）车辆－轨道－路基非线性耦合系统交叉迭代算法可模拟轮轨接触之间及材料的非线性行为，同时避免了求解方程系数矩阵的非对称性，具有求解精度高、可对两个子系统独立求解的优点。由于采用了交叉迭代算法，其不足之处是计算效率偏低。

2）采用新型车辆单元和轨道单元模型可以建立将运动的车辆与轨道结构进行耦合的显示算法，因而该方法具有计算精度高、程序编制容易，尤其适合分析整趟列车通过时轨道结构振动的特点。

3）运用列车轨道系统动态分析的移动单元法，可以使运动的列车始终处于轨道的中央，远离边界，因而可以最大限度地消除模型的边界效应，减小模型规模，提高计算效率。其不足之处是必须假定轨道基础是连续、均匀支撑的，这与多数情况下属于点支撑的实际轨道结构是有差别的。

4）轨道结构振动的双层梁、三层梁和四层梁模型考虑了移动车辆的轴荷载和因轨道随机不平顺引起的簧下质量的动荷载，采用快速离散傅里叶变换算法求解，具有计算效率高，尤其适合分析多节组合车辆通过时轨道结构振动的特点。其不足之处也是必须假定轨道基础是连续、均匀支撑的。

5）有限元与边界元耦合法是分析轨道－路基－大地系统动态响应的有效数值方法，运用边界元法可以精确满足半无限域边界条件和分析路基－大地系统的动力特性。

在了解了上述各种方法的特点后，为了提高计算精度和计算效率，根据分析问题的特点可以选择不同的模型和算法。

[1]KNOTHE K L，GRASSIE S L.Modeling of railway trackand vehicle track interaction at high-frequencies[J].Veh Syst Dyn，1993，314（22）：209-262.

[2]GRASSIE S L，GREGORY R W，JOHNSON K L.The dynamic response of railway track to high frequency lateral excitation[J].J Mech Eng Sci，1982，24（2）：91-95.

[3]GRASSIE S L，GREGORY R W，JOHNSON K L.The dynamic response of railway track to high frequency longitudinal excitation[J].J Mech Eng Sci，1982，24（2）：97-102.

[4]MATHEWS P M.Vibrations of a beam on elastic foundation[J].Zeitschrift furAngewandte Mathematik und Mechanik.1958，38：105-115.

[5]MATHEWS P M.Vibrations of a beam on elastic foundation II[J].Zeitschrift fur Angewandte Mathematik und Mechanik，1959，39：13-19.

[6]TROCHANIS A M，CHELLIAH R，BIELAK J.Unified approach for beams on elastic foundation for moving load[J].Journal of Geotechnical Engineering，1987，112：879-895.

[7]ONO K，YAMADAM.Analysis of railway track vibration[J].Journal of Sound and Vibration，1989，130：269-297.

[8]JEZEQUEL L.Response of periodic systems to a moving load[J].Journal ofApplied Mechanics，1981，48：613-618.

[9]TIMOSHENKO S，YOUNG D H，WEAVER J R.Vibration Problems in Engineering[M].4th ed，New York：John Wiley&Sons，Inc，1974.

[10]WARBURTON G B.The Dynamic Behavior of Structures[M].Oxford：Pergamon Press，1976.

[11]CAI C W，CHEUNG Y K，CHAN H C.Dynamic response of infinite continuous beams subjected to a moving force-an exact method[J].Journal of Sound and Vibration，1988，123（3）：461-472.

[12]VENANCIO FILHO F.Finite element analysis of structures under moving loads[J].Shock and Vibration Digest，1978，10：27-35.

[13]OLSSON M.Finite element，modal co-ordinate analysis of structures subjected to moving loads[J].Journal of Sound and Vibration，1985，99（1）：1-12.

[14]FRYBA L，NAKAGIRI S，YOSHIKAWA N.Stochastic finite element for a beam on a random foundation with uncertain damping under a moving force[J].Journal of Sound and Vibration，1993，163：31-45.

[15]THAMBIRATNAM DAVID P，YAN ZHUGE.Finite element analysis of track structures[J].Journal of Microcomputers in Civil Engineering，1993，8：467-476.

[16]THAMBIRATNAM D，ZHUGE Y.Dynamic analysis of beams on an elastic foundation subjected to moving loads[J].Journal of Sound and Vibration，1996，198（2）：149-169.

[17]NIELSEN J C O，IGELAND A.Vertical dynamic interaction between train and track-influence of wheel and track imperfections[J].Journal of Sound and Vibration，1995，187（5）：825-839.

[18]ZHENG D Y，FAN S C.Instability of vibration of a moving train and rail coupling system[J].Journal of Sound and Vibration，2002，255（2）：243-259.

[19]KOH C G，ONG J S Y，CHUAD K H，et al.Moving element method for train-track dynamics[J].Int J Numer Mech Engng，2003，56：1549-1567.

[20]AUERSCH L.Dynamic axle loads on tracks with and without ballast mats：numerical results of three-dimensional vehicle-track-soil models[J].Proc IMechE，Part F：J Rail and Rapid Transit，2006，220：169-183.

[21]CLOUTEAU D，ARNST M，AL-HUSSAINI T M，et al.Freefield vibrations due to dynamic loading on a tunnel embedded in a stratified medium[J].Journal of Sound and Vibration，2005，283（1/2）：173-199.

[22]ANDERSEN L，JONES C J C.Vibration from a railway tunnel predicted by coupled finite element and boundary element analysis in two and three dimensions[C]//Proceedings of the 4th Structural Dynamics-EURODYN.Munich，Germany，2002：1131-1136.

[23]ANDERSEN L，JONES C J C.Coupled boundary and finite element analysis of vibration from railway tunnels-a comparison of two and three-dimensional models[J].Journal of Sound and Vibration，2006，293（3/5）：611-625.

[24]THOMAS D.Dynamics of a high-speed rail vehicle negotiating curves at unsteady crosswind[J].Proceedings of the Institution of Mechanical Engineers：Part F，Journal of Rail and Rapid Transit，2010，224（6）：567-579.

[25]GANESH BABU K，SUJATHA C.Track modulus analysis of railway track system using finite element model[J].Journal of Vibration and Control，2010，16（10）：1559-1574.

[26]CAI Y，CAO Z，SUN H，et al.Effects of the dynamic wheel-rail interaction on the ground vibration generated by a moving train[J].International Journal of Solids and Structures，2010，47（17）：2246-2259.

[27]翟婉明.车辆－轨道垂向系统的统一模型及其耦合动力学原理[J].铁道学报，1992，14（3）：10-21.

[28]翟婉明.车辆－轨道耦合动力学[M].北京：中国铁道出版社，1997.

[29]翟婉明.车辆－轨道耦合动力学研究的新进展[J].中国铁道科学，2002，23（4）：1-13.

[30]雷晓燕.轮轨相互作用有限元分析[J].铁道学报，1994，16（1）：8-17.

[31]雷晓燕.高速列车对道碴的动力影响[J].铁道学报，1997，19（1）：4-11.

[32]雷晓燕.轨道动力学理论模型参数研究[J].铁道工程学报，1998（2）：26-31.

[33].雷晓燕.铁路轨道结构数值分析方法[M].北京：中国铁道出版社，1998.

[34]徐志胜，翟婉明，王开云，等.车辆－轨道系统振动响应分析——Timoshenko梁与Euler梁轨道模型的比较[J].地震工程与工程振动，2003，23（6）：74-79.

[35]徐志胜，翟婉明，王开云.基于Timoshenko梁模型的车辆－轨道耦合振动分析[J].西南交通大学学报，2003，38（1）：22-27.

[36]谢伟平，镇斌.移动荷载下Winkler梁稳态动力响应分析[J].武汉理工大学学报，2005，27（7）：61-63.

[37]罗雁云，施董燕，谭晓春.纵向力作用下无缝线路动态特性有限元分析[J].力学季刊，2008，29（2）：284-290.

[38]魏庆朝，邓亚士，冯雅薇.直线电机地铁轨道结构振动特性研究[J].铁道建筑，2008（3）：84-88.

[39]高亮，陶凯，曲村，等.客运专线桥上无缝道岔空间力学特性的研究[J].中国铁道科学，2009，30（1）：29-34.

[40]冯青松，雷晓燕，练松良.高速铁路路基－地基系统振动响应分析[J].铁道科学与工程，2010，7（1）：1-6.

[41]边学成，陈云敏.列车荷载作用下轨道和地基的动响应分析[J].力学学报，2005，37（4）：477-484.

[42]边学成.高速列车运动荷载作用下地基和隧道的动力响应分析[D].杭州：浙江大学，2005.

[43]边学成，陈云敏.列车移动荷载作用下分层地基响应特性[J].岩石力学与工程学报，2007，26（1）：182-189.

[44]谢伟平，胡建武，徐劲.高速移动荷载作用下的轨道一地基系统的动力响应[J].岩石力学与工程学报，2002，21（7）：1075-1078.

[45]谢伟平，王国波，于艳丽.移动荷载引起的土变形计算[J].岩土工程学，2004，26（3）：318-322.

[46]聂志红，刘宝琛，李亮，等.移动荷载作用下轨道路基动力响应分析[J].中国铁道科学，2006，27（2）：15-19.

[47]雷晓燕.轨道临界速度与轨道强振动研究[J].岩土工程学报，2006，28（3）：419-422.

[48]雷晓燕.轨道结构动力分析的傅里叶变换法[J].铁道学报，2007，29（3）：67-71.

[49]雷晓燕.高速列车诱发地面波与轨道强振动研究[J].铁道学报，2006，28（3）：78-82.

[50]雷晓燕.高速铁路轨道振动与轨道临界速度的傅里叶变化法[J].中国铁道科学，2007，28（6）：30-34.

[51]和振兴，翟婉明.高速列车作用下板式轨道引起的地面振动[J].中国铁道科学，2007，28（2）：7-11.

[52]李志毅，高广运，冯世进，等.高速列车运行引起的地表振动分析[J].同济大学学报：自然科学版，2007，35（7）：909-914.

[53]WU YEANSENG，YANG YEONGBIN.A semi-analytical approach for analyzing ground vibrations caused by trains moving over elevated bridges[J].Soil Dynamics and Earthquake Engineering，2004，24：949-962.

[54]XIA H，CAO Y M，ROECK G DE.Theoretical modeling and characteristic analysis of moving-train induced ground vibrations[J].Journal of Sound and Vibration，2010，329：819-832.

[55]刘学毅，王平，万复光.轮轨空间耦合振动分析模型及其应用[J].铁道学报，1998，20（3）：102-108.

[56]李德建，曾庆元.列车－直线轨道空间耦合时变系统振动分析[J].铁道学报，1997，19（1）：101-107.

[57]梁波，蔡英，朱东生.车－路垂向耦合系统的动力分析[J].铁道学报，2000，22（5）：65-71.

[58]苏谦，蔡英.高速铁路路基结构空间时变系统耦合动力分析[J].西南交通大学学报，2001，36（5）：509-513.

[59]王其昌，蔡成标，罗强，等.高速铁路路桥过渡段轨道折角限值分析[J].铁道学报，1998，20（3）：109-113.

[60]罗强，蔡英，翟婉明.高速铁路路桥过渡段的动力学性能分析[J].工程力学，1999，16（5）：65-70.

[61]罗强，蔡英.高速铁路路桥过渡段变形限值与合理长度研究[J].铁道标准设计，2000（6/7）：2-4.

[62]王平.道岔区轮轨系统动力学的研究[D].成都：西南交通大学，1997.

[63]任尊松.车辆—道岔系统动力学研究[D.成都：西南交通大学，2000.

[64]陈果.车辆轨道耦合系统随机振动分析[D].成都：西南交通大学，2000.

[65]雷晓燕.轨道力学与工程新方法[M].北京：中国铁道出版社，2002.

[66]雷晓燕，毛利军.线路随机不平顺对车辆－轨道耦合系统动力响应分析[J].中国铁道科学，2001，22（6）：38-43.

[67]LU F，KENNED D Y，WILLIAMS F W，et al.Symplectic analysis of vertical random vibration for coupled vehicle-track systems[J].Journal of Sound and Vibration，2008，317 ：236-249.

[68]LEI XIAOYAN，NAO-AKI NODA.Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile[J].Journal of Sound and Vibration.2002，258（1）：147-165.

[69]雷晓燕，圣小珍.现代轨道理论研究[M].2版.北京：中国铁道出版社，2006.

[70]LEI XIAOYAN，ZHANG BIN.Influence of track stiffness distribution on vehicle and track interactions in track transition[J].Proceedings of the I MECH E Part F：Journal of Rail and Rapid Transit，2010，224（1）：592-604.

[71]雷晓燕，张斌，刘庆杰.轨道过渡段动力特性的有限元分析[J].中国铁道科学，2009，30（5）：15-21.

[72]雷晓燕，张斌，刘庆杰.列车－轨道系统竖向动力分析的车辆轨道单元模型[J].振动与冲击，2010，29（3）：168-173.

[73]雷晓燕.客货混运铁路专线轨道振动分析[J].铁道工程学报，2007（3）：16-20.

[74]LEI XIAOYAN，JERRY G ROSE.Track vibration analysis for railways with mixed passenger and freight traffic[J].Proceedings of the I MECH E Part F：Journal of Rail and Rapid Transit，2008，222（4）：413-421.

[75]LEI XIAOYAN，JERRY G ROSE.Numerical investigation of vibration reduction of ballast track with asphalt trackbed over soft subgrade[J].Journal of Vibration and Control，2008，14（12）：1885-1902.

[76]STAVROS A SAVIDIS，REINHOLD HIRSCHAUER，CHRISTOPHER BODE，et al.3D-simulation of dynamic interaction between track and layered subground[C]//Karl Popp and Werner Schiehlen.System Dynamics and Long-term Behaviour of Railway Vehicles，Track and Subgrade.Berlin：Springer-Verlag Berlin Heideberg，2003：431-450.

[77].雷晓燕.岩土工程数值计算[M].北京：中国铁道出版社，1999.

Progress in the Development of Track Dynamic Models andAssociated Numerical Methods

Lei Xiaoyan
（Engineering Research Center of Railway Environment Vibration and Noise，Ministry of Education，East China Jiaotong University，Nanchang 330013，China）

With increase of train speeds and axle loads，interactions between the vehicle and the track are being intensified.Studying wheel/rail interaction mechanism thoroughly is very important to safety and stability of high speed and heavy railways in operation.In this paper，a brief literature review is given for the progress of numerical models employed in track dynamics，followed by introductions of five track dynamic models and associated numerical methods，i.e.，crossing and iterative algorithm for non-linear vehicle，track and subgrade coupling system，new types of vehicle element and track element，moving element method for train-track dynamics，multi-layer beam models subjected to moving loads at constant velocity along an infinite track，and dynamic analysis of track，subgrade and soil system by coupling finite elements with boundary elements.Merits and drawbacks for above five approaches are discussed.These models and numerical approaches are important basis and means in analyses of track dynamics.In order to improve computational accuracy and efficiency，suitable approaches should be chosen based on characteristics of the concerned problem.

track dynamics；crossing and iterative algorithm；vehicle element；track element；moving element；coupling finite elements with boundary elements

U213.212

A

1005-0523（2011）03-0001-12

2011-02-21

国际科技合作与交流专项项目（2010DFA82340）；国家自然科学基金项目（50978099）

雷晓燕（1956－），男，教授，博士，主要研究方向为高速铁路轨道动力学。

book=10,ebook=215