一种基于双子群的改进粒子群优化算法*
2011-03-06张英杰张英豪罗春松
张英杰,李 亮,张英豪,罗春松
(1.湖南大学计算机与通信学院,湖南长沙 410082;2.湖南机电职业技术学院,湖南长沙 410151)
一种基于双子群的改进粒子群优化算法*
张英杰1†,李 亮1,张英豪2,罗春松1
(1.湖南大学计算机与通信学院,湖南长沙 410082;2.湖南机电职业技术学院,湖南长沙 410151)
针对粒子群优化算法易于陷入局部最优解并存在早熟收敛的问题,提出了一种基于双子群的改进粒子群优化算法(TS-IPSO),通过2组搜索方向相反的主、辅子群之间的相互协同,扩大搜索范围,借鉴遗传算法的杂交机制,并采用惯性权值的非线性递减策略,加快算法的收敛速度和提高粒子的搜索能力,降低了算法陷入局部极值的风险.实验结果表明该算法较标准PSO算法提高了全局搜索能力和收敛速度,改善了优化性能.
收敛性;粒子群优化算法;子群;杂交机制;遗传算法
粒子群优化算法(Particle Swarm Op timization,PSO)是一种基于群体的演化算法,是通过群体内粒子间的合作与竞争产生的群体智能指导优化策略,最早由Kennedy和Eberhart于 1995年提出的[1].该算法操作简单,前期收敛速度快、设置参数少、容易实现、能有效地解决复杂优化问题,在函数优化、模式识别、机器人学习、组合优化以及一些工程领域得到了广泛应用.但由于PSO算法的数学基础相对薄弱,存在早熟收敛、搜索精度不高、后期迭代效率低[2]的缺点,尤其是当解空间为非凸集时,应用PSO算法容易在后期陷入局部极优点.针对这些问题,目前出现了许多改进算法,如文献[3]用动态调整惯性权重来平衡搜索能力和收敛速度;文献[4]通过对粒子位置或速度引入一个小概率随机变异操作来增强种群的多样性,使算法能有效地进行全局搜索;文献[5]提出了一种带有混沌变异算子的量子粒子群优化算法,文中利用混沌序列代替随机序列从而增加粒子的多样性,防止粒子陷入局部收敛;文献[6]提出了一种新的双子群PSO算法(TSPSO).
大量研究实验表明,设法保持种群的多样性,或引入跳出局部最优点的机制,或与其他算法融合可以克服全局优化算法早熟收敛.鉴于此,本文在文献[6]的基础上提出了一种改进粒子群优化算法(TSIPSO),该算法在不增加粒子规模的情况下充分扩展搜索范围,挖掘搜索域内的有用信息,并借鉴了遗传算法的杂交机制,还采用惯性因子的非线性递减策略,以有效地提高粒子的探索能力,解决粒子群算法的局部收敛问题.
1 标准粒子群优化算法
PSO算法通过模拟鸟群捕食行为实现优化问题的求解.首先在解空间内随机初始化鸟群,鸟群中的每一只鸟称为粒子,这些粒子在解空间内按照某种规则移动,经过若干次修正后找到最优解.在每一次修正中,粒子通过跟踪两个极值来更新自己的速度和位置.一个是粒子本身的最优解p,另一个是整个种群目前找到的最优解g.每个粒子根据p和g修正自身的飞行方向和飞行速度,使得每个粒子最终能够发现并到达解空间内最优解位置.
假设搜索空间是D维,粒子群由m个粒子组成.Xi=(xi1,xi2,…,xid)表示D维空间中的第i个粒子,其速度为Vi=(vi1,vi2,…,vid),其最大值为一个指定阈值 V max.粒子的速度-位置进化方程为:

式中:i=1,2,…,m;d=1,2,…,D;C1,C2为非负常数,一般取2.0;rand1,rand2为介于[0,1]之间服从均匀分布的随机数;Pi=(pi1,pi2,…,pid)为粒子i当前所经历的最优位置,称为个体最优位置;Pg =(pg1,pg2,…,pg d)为群体中所有粒子所经历的最优位置,称为全局最优位置.惯性权值ω按式(3)线性递减:

式中:ωstart为始权值;ωend为终权值 ,并建议 ωstart和ωend分别取0.9和0.4;Iter max和Iter分别为最大迭代次数和当前迭代次数.
2 基于双子群的TS-IPSO算法
2.1 双子群PSO算法(TSPSO)[6]
TSPSO算法是一种操作简单、易于实现的双子群的PSO算法,其实现思想为:在随机初始化一组粒子群之后,将其等分为2个相互独立的子群,其中一组子群按标准PSO算法迭代搜索,称为主子群;另一组子群沿主子群的相反方向迭代搜索,即位置进化方程按下式更新:

该子群称为辅子群.在每次迭代结束时,比较2个子群个体最优位置所对应的适应值大小,适应值较差的个体最优粒子被更优者替代.这样通过主、辅2个子群相互补充、协同进化,在不增加粒子规模的情况下,充分扩展搜索范围,挖掘搜索域内的有用信息,降低PSO算法陷入局部最优点的风险.
2.2 杂交机制
遗传算法是模拟达尔文的自然选择学说的生物进化过程的一种计算模型,是一种随机搜索最优化计算方法,具有的基本操作运算是选择、杂交和变异等.文献[2]借鉴遗传算法的杂交操作运算思想,最早提出了杂交PSO算法的概念.该算法在每次迭代中,选取指定数量的粒子放入一个池中,种群中被选中的粒子被赋予了一个随机的与适应值无关的杂交概率,依据杂交概率对池中的粒子随机进行杂交操作,产生同样数目的孩子粒子,并用孩子粒子代替父母粒子,以保持种群的粒子数目不变.孩子粒子位置由父母粒子位置的算数加权来计算[7],即

式中:X1(t)和X2(t)为选择进行杂交操作的粒子,且都是D维的位置向量;r为D维均匀分布的且每个分量都在[0,1]取值的随机向量.
孩子粒子的速度由下面的公式得到:

式中:V1(t)和V2(t)为进行杂交操作的双亲粒子的速度.这样,子代粒子的位置和速度的信息来自父代粒子的位置和速度的交叉操作.交叉操作使后代粒子继承了双亲粒子的优点,这在理论上加强了对粒子间区域的搜索能力.假设两个双亲粒子均处于不同的局部最优区域,那么两者交叉产生的后代粒子往往能够摆脱局部最优,获得改进的搜索结果.数值实验结果表明,杂交粒子群算法比原始粒子群算法搜索速度更快,收敛精度更高.
2.3 惯性因子选择策略
惯性权值ω的取值对算法性能有影响,如果 ω的取值随着算法迭代的进行而线性减小,那么算法的性能可明显地得到改善.若ω取值较大,则粒子的全局搜索能力较强;若ω取值较小,则粒子的局部挖掘能力增强.
根据文献[8]选择一种自适应的非线性惯性权值递减函数,具体表达式为:
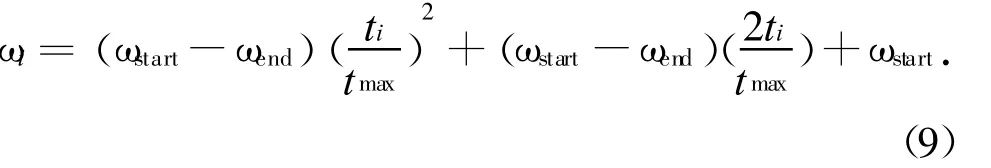
式中:t max为群体的最大迭代次数;ti为当前的迭代代数;ωstart,ωend分别为初始惯性权重的最大值和最小值.以式(9)构造的惯性因子,初期具有最大值,迭代的最后一步达到最小值,中间迭代周期是非线性减小的,目的是在迭代的早期加大惯性权值的递减速度来让算法更快地进入局部搜索,均衡全局和局部搜寻能力.文献[8]证明了采用惯性因子非线性递减机制的算法性能相对线性缩小惯性因子的PSO的收敛速度更快,能获得更好的求解质量.
2.4 TS-IPSO的算法步骤
综上所述,本文提出了一种新的粒子群优化算法 ——基于双子群的改进粒子群算法(TS-IPSO),其算法步骤如下:
1)随机初始化粒子群中粒子的位置与速度.
2)将随机初始化的粒子群等分为2组子群.计算每个粒子的适应值,设置Pi为初始群体的当前位置,Pg为最优粒子位置.
3)判断算法收敛准则是否满足,如果满足执行8),否则转向4).
4)主子群根据式(1),式(2)和式(9)更新粒子的位置与速度,辅子群按式(1),式(4)和式(9)更新粒子的位置与速度;并对主、辅子群进行速度、位置限制.当Vi>V max或Vi<V m in时,则令Vi=V max或Vi=Vmin;当 Xi>Xmax或 Xi<Xmin时 ,则令 Xi= X max或Xi=X min.
5)更新主、辅子群个体最优位置和全局最优位置,如果粒子的适应值优于Pi的适应值,则Pi更新为新位置,反之保持不变;如果粒子的适应值优于Pg的适应值,则Pg更新为新位置,反之保持不变;然后比较两组子群的个体最优位置所对应的适应值,优者更新为两组子群共同的个体最优位置.同样,比较两组子群的全局最优位置所对应的适应值,优者更新为整个粒子群的全局最优位置.
6)根据适应度值计算每个个体的选择概率,通常按线性排名计算.
7)执行选择、杂交操作,按式(7),式(8)对每2个粒子的速度进行杂交操作,若当Vi>V max或Vi<Vmin时,则令Vi=Vmax或Vi=Vmin;按式(5),式(6)对每2个粒子的位置进行杂交操作,若当Xi>X max或Xi<X min时,则令Xi=X max或Xi=X m in,生成新一代种群.
8)检查是否满足PSO算法终止条件,若否,转向4),继续;若是,则求出最优解.
3 TS-IPSO算法仿真
下面采用4个基准测试函数[9]来评价所提出的基于双子群的改进粒子群算法(TS-IPSO)的性能,并与标准PSO算法进行了比较.这4个基准测试函数如下所示:

其中:函数f1(x)为一个简单的单峰函数,在(0,0,…,0)达到极小值;f2(x)的全局极小点在xi=0(i =1,2,…,n),且有众多的局部极小点,可用来考查算法避免陷入局部最优点,并进行全局探索的能力; f3(x)为具有大量局部极值点的多峰函数,一般算法难以求得最优解,且函数存在一个全局最小值f min=0;f4(x)是一个非凸函数,在(1,1,…,1)时达到最小值0.文献[10]论述了上述4个函数能有效验证PSO算法的寻优性能及代表性.4个测试函数的参数设置如表1所示.

表1 4个基准测试函数的参数设置Tab.1 Parameter settings of four benchmark functions
在TS-IPSO算法中,学习因子 C1,C2均取1.496 2,rand1,rand2为在区间[0,1]内均匀分布的随机数,惯性权重 ω按照式(9)进行计算.每个函数运行50次,以平均值作为优化结果.通过表2的数据可以看出,本文提出的TS-IPSO算法的寻优结果,无论是50次优化运行得到的函数最优解或是平均最优解,都明显优于标准PSO算法的优化结果.

表2 实验结果Tab.2 Experiment results
为了更直观地体现TS-IPSO算法的性能,分别将4个测试函数迭代的收敛曲线与标准PSO算法的寻优曲线进行对比,如图1~图4所示.
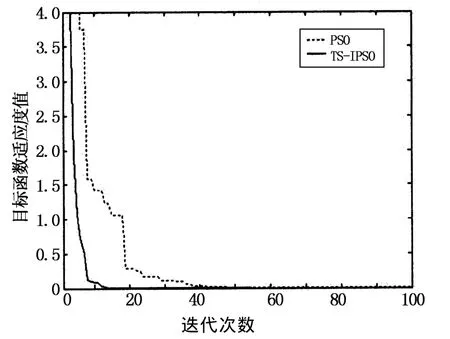
图1 Sphere函数寻优曲线Fig.1 Comparison of optim izing process on Sphere function

图2 G riewank函数寻优曲线Fig.2 Comparison of optim izing process on Griewank function

图3 Rastrigin函数寻优曲线Fig.3 Com parison of op tim izing process on Rastrigin function

图4 Rosenbrock函数寻优曲线Fig.4 Comparison of optim izing process on Rosenbrock function
由图1~图4可知,本文提出的TS-IPSO算法的优化效果和优化过程明显好于标准PSO算法.对于函数 f1(x),f2(x)和 f3(x),本文算法都取得了理论最优值,都能经过较少的迭代次数而获得最优解;对于 f4(x),改进算法也取得了较标准PSO算法更好的结果.同时对于搜索目标函数全局最优值,标准PSO算法不是陷入局部极值,就是计算逐步趋于停顿,而基于双子群的TS-IPSO算法则表现出更为强大的搜索能力和更快的收敛速度.
4 结 语
基于双子群的改进粒子群算法TS-IPSO以搜索方向相反的主、辅2组子群协同搜索,扩展了搜索范围,结合遗传算法的杂交机制并采用惯性因子非线性递减策略,具有良好的优化效果和探索性能,从而降低了优化算法陷入局部最优点的风险,同时加快了收敛速度.实验表明该算法不仅具有较强的全局搜索能力,而且能有效避免常规算法的早熟收敛问题,显著提高了优化性能.
[1] KENNEDY J,EBERH ART R C.Particle sw arm algorithm [C]//Proceedingsof the 1995 IEEE In ternational Conference on Neu ral Netw orks.New York:IEEE Press,1995,4:1942-1948.
[2] ANGELINE P J.Evolutionary optim ization versus particle swarm optim ization:philosophy and performance differences [C]//Proceedings of the 7th Annual Conference on Evolutionary Programm ing.Berlin:Springer,1998:601-610.
[3] KENNEDY J,EBERHART R C.A discrete binary version of the particle swarm algorithm[C]//Proceedingsof IEEE Conference on Systems,M an and Cybernetics.Orlando:IEEE, 1997:4104-4109.
[4] X IE X F,ZHANG W J,YANG Z L.A dissipative particle swarm optim ization[C]//Proc of the IEEE IntConf on Evolutionary Com putation.H onolulu:IEEE,2002:1456-1461.
[5] LEANDRO DOS SANTOS COELHO.A quan tum particle sw arm op tim izer with chaotic mu tation operator[J].Chaos, Solitons and F ractals,2008,37(5):1409-1418.
[6] 焦巍,刘光斌.动态环境下的双子群PSO算法[J].控制与决策,2009,24(7):1083-1091.
JIAOW ei,LIU Guang-bin.Tw o subpopu lation sw arm PSO algorithm in dynamic environment[J].Control and Decision, 2009,24(7):1083-1091.(In Chinese)
[7] 曹春红,张永坚,李文辉.杂交粒子群算法在工程几何约束求解中的应用[J].仪器仪表学报,2004,25(增刊4):397-400.
CAO Chun-hong,ZHANG Yong-jian,LIWen-hui.The application of crossb reeding particle sw arm optim izer in the engineering geometric constraint solving[J].Chinese Journal of Scientific Instrument,2004,25(Sup4):397-400.(In Chinese)
[8] 陈贵敏,贾建援,韩琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报,2006,40(1):53-56.
CHEN Gui-m in,JIA Jian-yuan,H AN Qi.Study on the strategy of decreasing inertiaweigh t in particle swarm op timization algorithm[J].Journal of Xi'an Jiaotong University,2006,40 (1):53-56.(In Chinese)
[9] 王俊伟,汪定伟.一种带有梯度加速的粒子群算法[J].控制与决策,2004,19(11):1298-1230.
WANG Jun-wei,W ANG Ding-wei.Partic le sw arm optim ization algorithm w ith g radient acceleration[J].Controland Decision, 2004,19(11):1298-1230.(In Chinese)
[10]曾建潮,介蜻,崔志华.微粒群算法[M].北京:科学出版社, 2004:11-51.
ZENG Jian-chao,JIE Qing,CUI Zhi-hua.Partic le sw arm optim ization[M].Beijing:Science Press,2004:11-51.(In Chinese)
An Im proved Particle Swarm Op timization A lgorithm Based on Two-subpopulation
ZHANG Ying-jie1†,LI Liang1,ZHANG Ying-hao2,LUO Chun-song1
(1.Co llege of Computer and Communication,H unan Univ,Changsha,H unan 410082,China; 2.H unan Mechanical and Electrical Polytechnic,Changsha,H unan 410151,China)
Particle Sw arm Optimization algorithm easily gets stuck at localoptimal solution and shows premature convergence.An imp roved Particle Swarm Optimization algorithm based on tw o-subpopu lation(TS-IPSO)was proposed.Thesearch range of the algorithm w asextended through main subpopulation particle swarm and assistant subpopulation particle swarm,w hose search direction was inversed comp letely.It also adopts the crossbreeding mechanism in genetic algorithm,and uses non-linear inertia weight reduction strategy to accelerate the op timization convergence and improve the search capabilitiesof particles,then effectively decrease the risk of trapping into localoptima. Experiment resultshave shown that the TS-IPSO can greatly improve the global convergence ability and enhance the rate of convergence,compared with SPSO.
convergence;Particle Swarm Optimization(PSO)algorithm;subpopulation;crossbreeding;genetic arithmetic
TP18
A
1674-2974(2011)01-0084-05 *
2010-05-30
国家自然科学基金资助项目(60634020);湖南省科技计划重点资助项目(2010GK 2022)
张英杰(1970-),男,湖南邵阳人,湖南大学副教授,博士
†通讯联系人,E-mail:zy j18502@hnu.cn
