Chirp信号的去噪研究及其Matlab实现

苏 凯，蒋宇中，刘月亮，张书南

(海军工程大学 电子工程学院，湖北 武汉 430033)

0 引言

Chirp信号是瞬时频率在某个范围内随时间变化的正弦波,因其良好的频带利用率，在通信，雷达，声纳等领域都具有广泛的应用。以通信为例，Chirp信号可以作为载波与BPSK，DPSK，QPSK等各种数字调制方式相结合以实现通信的目的[1]。

Chirp调制解调器是一种中低速的高质量调制解调器,这类调解器因其很强的可靠性和鲁棒性,被认为是一种适合短波信道的数传工具。Chirp信号具有较强的抗干扰、低耗低时延、抗多径效应和抗多普勒衰减等能力，正逐渐受到人们的关注。但由于短波信道的复杂性和不稳定性，信号易受噪声干扰，影响通信质量。因此研究其去噪问题，具有重要意义。实验利用LPC分析工具和小波分析工具对Chirp信号的去语音噪声问题进行了研究，并在Matlab上进行仿真，获得了良好效果。

介绍了Chirp-BPSK调制方式，并以电台采集的语音样本作为噪声对其去噪问题进行了研究。

1 信号模型

1.1 Chirp-BPSK调制信号的构成

Chirp信号在一个码元周期内的表达式为[2]：

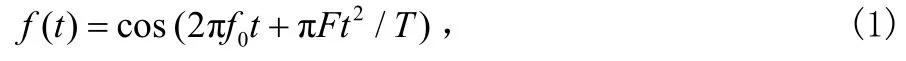
f0为中心频率，F为扫频带宽，T为码元持续时间。

Chirp-BPSK信号是以Chirp信号为载波，利用其相位的变化来传递数字信息的。可表述为一个双极性全占空比矩形脉冲与Chirp信号的相乘，时域表达式为：

时域波形图如图1所示（实验数据 f0取300 Hz, F为1 700 Hz，T为0.1 s）

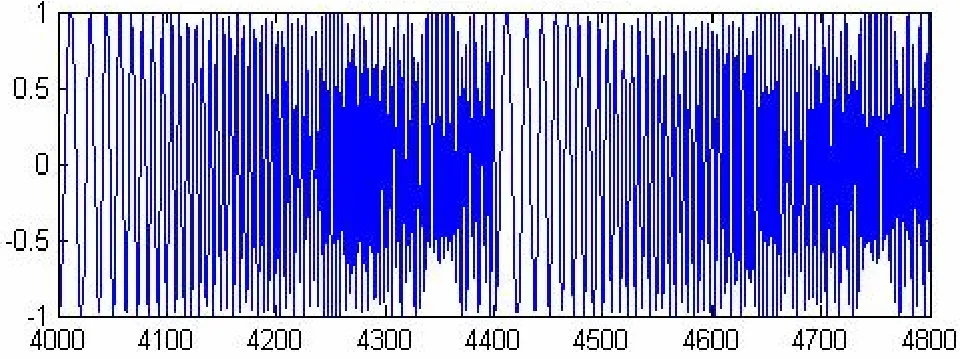
图1 Chirp-BPSK 时域波形

1.2 接收信号模型

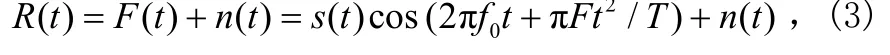
F(t)为发送信号，n(t)为噪声，这里的n(t)采用电台采集的语音作为噪声样本，电台采样率为8 000 Hz.因此问题核心在于如何消除含噪信号中的语音噪声。此实验分别采用LPC和小波分析对接收信号进行处理，得到语音噪声估计。然后由含噪信号减去噪声估计值得到去噪信号。

2 LPC分析

由于语音信号的短时平稳性，使得对它的处理一般可以采用短时处理技术，即对信号进行分帧处理。LPC分析是目前应用广泛的一种特征参数提取技术。它建立了一种与人的声道相对应的全极点模型[3]：

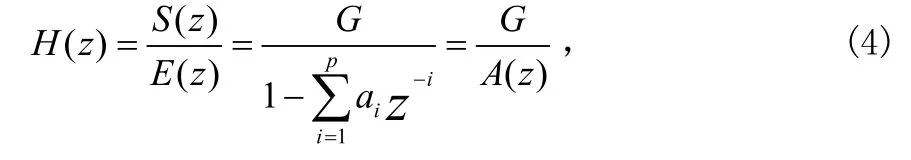
其中p为预测器阶数，一般取10～14，G为声道滤波器增益。因此语音抽样s(n)和激励信号e(n)之间的关系可用以下方程来表示：

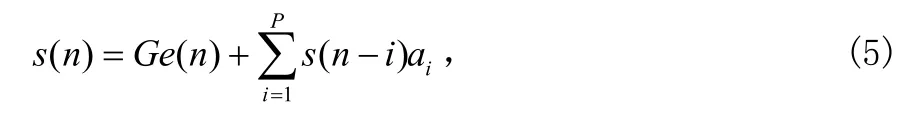
即语音抽样之间具有短时相关性，可以用过去的样点值预测未来样点值。预测误差ε(n)为：

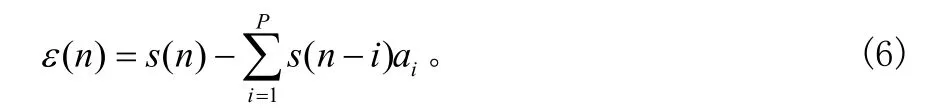
只要对给定语音序列，得到预测系数的最佳估值ai，就可以达到线性预测的目的。文献[3]利用最小方均误差作为估计模型参数的准则得到ai，在此不作累述。利用LPC分析工具，可以对含噪信号中的语音噪声n(t)进行线性预测，达到消除语音噪声的目的。

3 小波分析原理

3.1 小波变换原理

[4]。若信号Ψ(t)∈L2(R)，其中L2(R)表示(-∞,∞)上的平方可积函数空间，且其Fourier变换满足：

则称Ψ(t)为一个小波母函数或基本小波。将小波函数Ψ(t)进行伸缩和平移得到小波函数族：

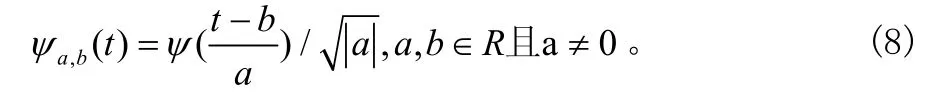
其中,a为伸缩因子，b为平移因子，则对于任意f(t),其小波变换定义为：

在实际数据处理中通常采用离散小波变换:

j,k,ψj,k(t)分别满足a=2j,k=b/a,ψj,k(t)=2−j/2ψ(2−jt-k)，j称作ψj,k(t)的尺度。

3.2 小波分解与重构

Mallat算法是一种快速的离散小波变换算法，它可以对信号进行分解和重构，算法为：

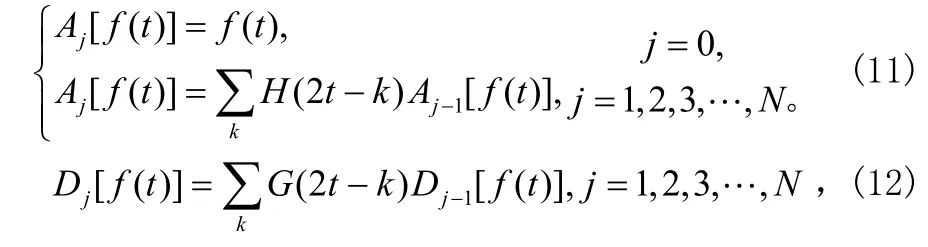
式中,t为离散时间，t=1,2,3…m；f(t)为离散信号；j为分解层数j=1,2,3…N，其中N=log2m；H,G 为一对正交镜像滤波器组。 Aj[f(t)]为低频部分的小波系数，代表f(t)尺度为j的逼近(近似部分),Dj[f(t)]为高频部分的小波系数，代表f(t)的逼近误差(细节部分)。可以通过以下算法由近似部分和细节部分的小波系数进行信号重构[5]：

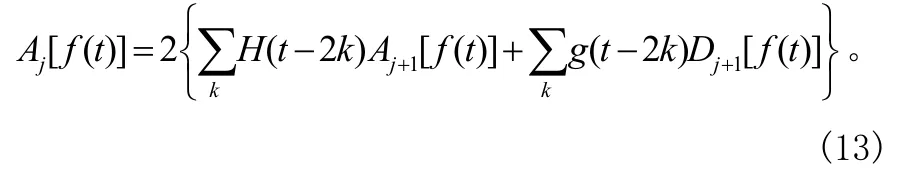
式（13）表示：信号f(t)在第j层的逼近 Aj[f(t)]，可由第j+1层的逼近 Aj+1(f(t))经过重构滤波器后和第j+1层的逼近误差 Dj+1(f(t))经过重构滤波器后所得值的和得到。经过层层迭代可以重构信号f(t)。

3.3 阈值去噪原理

参考文献[6]。语音信号是低频信号，可以通过小波变换使信号的能量在小波变换域集中于少数小波系数上。而噪声通常表现为高频信号，其能量分布于大量小波系数上。即意味着语音信号的小波系数值通常高于噪声的小波系数值。若对分解后的信号每一层的小波系数进行阀值处理再进行信号重构则可以滤除噪声。小波阀值去噪方法可以分为硬阀值法和软阀值法两种。阈值选取原则主要有无偏似然估计阈值、固定阈值、启发式阈值和极值阈值等。考虑到短波信道中的噪声比较大，实验采用无偏似然估计阈值，并使用软阈值法。

4 Matlab仿真与结果分析

4.1 Matlab仿真

实验采用电台采集的语音噪声作为噪声样本，含噪信号如图2所示（图2、图3、图4横坐标单位均为105）。

采用LPC工具对接收信号进行分析得到语音噪声估计，再由接收信号减去语音噪声估计，得到去噪信号，如图3所示。

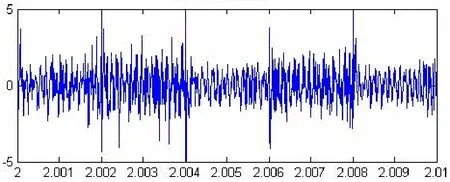
图3 LPC去噪信号

小波分析工具对接收信号进行分析得到语音噪声估计，再由接收信号减去语音噪声估计，得到去噪信号，如图4所示。

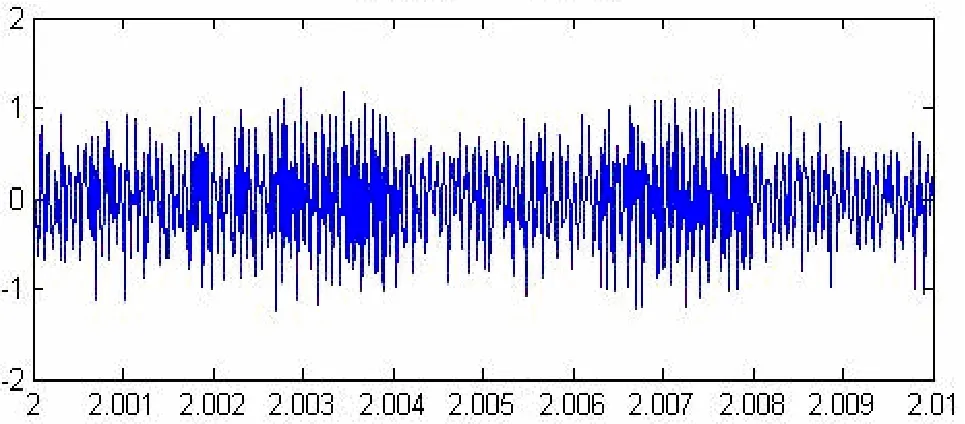
图4 小波去噪信号

由图3、图4可以得知，在两种工具分析去噪后，噪声均有大幅度的削减。

4.2 实验结果性能分析

为了比较两种方法的性能，采用相干解调法对含噪信号进行解调。由于语音噪声的不规律性，难以在时域波形上良好地反映去噪效果，该实验以接收端的信噪比和误码率性能作为评价体系，对去噪效果进行评估。图5代表信号未去噪，LPC分析去噪和小波分析去噪三种情况下信噪比/误码率性能对比图。

由图5表明,对未去噪的信号解调检测，其误码率为0.5左右，无法正确检测出发送码元，而经LPC分析去噪和小波分析去噪后，误码率性能则有显著提高。同时可以看出在该小波分析去噪较LPC分析去噪性能更为优越，具有更良好的去噪能力。

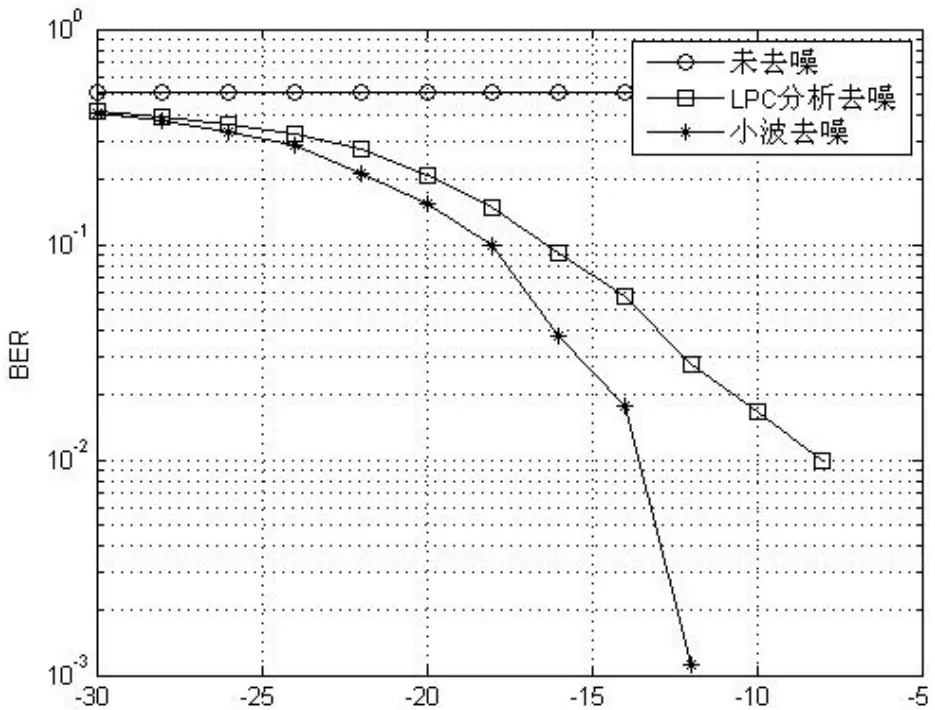
图5 信噪比/误码率性能对比

5 结语

针对工程实践中接收到的 Chirp信号噪声含量大的问题。通过 LPC分析工具和小波分析工具分别对 Chirp-BPSK信号中的语音噪声进行了去噪处理，并作出了相应的性能分析。由信噪比/误码率性能图可以得出结论：小波分析去噪较LPC分析去噪性能更为优越，信噪比，误码率性能均有较大幅度提升，具有良好的去噪能力，提高了通信质量。

参考文献

[1] 王晓炜,李昕,费敏锐.Chirp扩频通信系统抗噪声性能研究[J].通信技术,2009,42(03):1.

[2] DARBYSHIRE E P, GOTT G F.A Chirp Modem Incorporating Interference Excision[J].IEEE Proceedings-I,1992,139(04):3.

[3] 王彬.Matlab数字信号处理[M].北京：机械工业出版社，2010:306-309.

[4] 秦亚辉，冯景辉，陈立定.基于小波信号的信号去噪方法[J].信息技术，2010(01):1-2.

[5] 姜波，李迎盼，田日才.小波奇异性分析在DS-UWB降噪中的应用[J].通信技术，2010,43(01):2-3.

[6] 罗幼芝.小波变换应用于信号去噪研究[J].吉林师范大学学报:自然科学版，2005(02):1-3.