基于矩量法的线天线电磁散射和电磁辐射分析

高宝春 彭 戈 胡一峰

中国舰船研究设计中心，上海 201108

基于矩量法的线天线电磁散射和电磁辐射分析

高宝春 彭 戈 胡一峰

中国舰船研究设计中心，上海 201108

针对线电流模型分析半径／波长较大的线天线的缺点，首先利用解析法描述线天线的结构，将线天线模拟为细带模型，线面连接问题转化为面面连接问题，选取RWG函数对天线模型进行剖分，采用矩量法分析不同半径下偶极子天线的电流分布，辐射场，方向图，对散射模式和辐射模式的情况进行了比较。随后计算了有限平板上10m单极子天线的天线特性。计算结果表明，当半径／波长较小时，电流基本沿天线轴向流动，线电流模型适用于分析线天线的问题，半径／波长较大时，横向电流不可忽略，线电流模型不适用于分析线天线的问题。

矩量法；RWG基函数；线天线；电磁散射；电磁辐射

1 引言

线天线是最常用的天线形式之一，大到飞机、舰船，小到手机等移动通信设备都能见到线天线的使用，因此准确的分析线天线的电磁特性具有重要的实际意义。基于电场积分方程的矩量法能够准确的分析线天线的电磁特性［1］。

常见的线天线形式主要有偶极子天线和单级子天线两种，本文将分别对这2种天线形式进行研究。在分析线天线的问题时，通常将线天线作为一维分段模型加以研究，假设电流只沿天线的轴向方向流动，在横向方向上没有电流分布。在实际情况中，当天线的半径较小时，横向电流可以忽略不计，但当半径较大时，横向电流将不可忽略不计，此时，电流分布已不能近似为沿轴向方向的流动［2］。

在用矩量法分析线面连接的问题时，通常需要构造三类基函数，分别是线元之间，面元之间，线元与面元之间［3］。三类基函数的构造给分析和计算带来了较大的麻烦。部分文献［4］给出了一种用解析法描述天线结构的例子并受到了较大的关注［5-8］。本文采用这种方法，建立金属细带模型模拟线天线的结构，导体面和金属细带模型均通过RWG边元对其剖分，将线面连接问题转化为面面连接问题，给分析和计算带来了较大的方便。在此基础之上，分析了偶极子天线的散射特性与辐射特性，并对较少受关注的近场场强进行了计算。随后，对有限平面上的单根大功率单极子天线进行了仿真，给出了单极子天线的输入阻抗，并引入了组合单极子模型进行比较，分析两种模型下的近场场强与方向性图。

2 理论分析

2.1 电磁散射理论分析

对于电磁散射问题，假设有一入射场Ei照射在某理想导体表面产生感应电流J。Es为J在自由空间的辐射场，n为理想导体表面外法线单位矢量。Es可由下式表示：

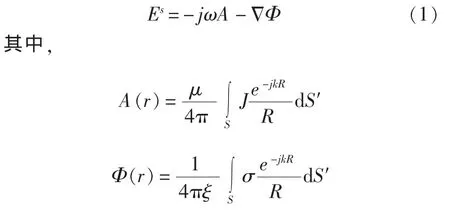
根据理想导体的边界条件 n×（Ei＋Es）＝0，得到：

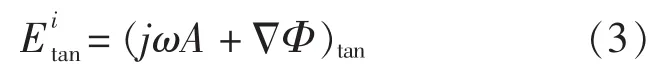
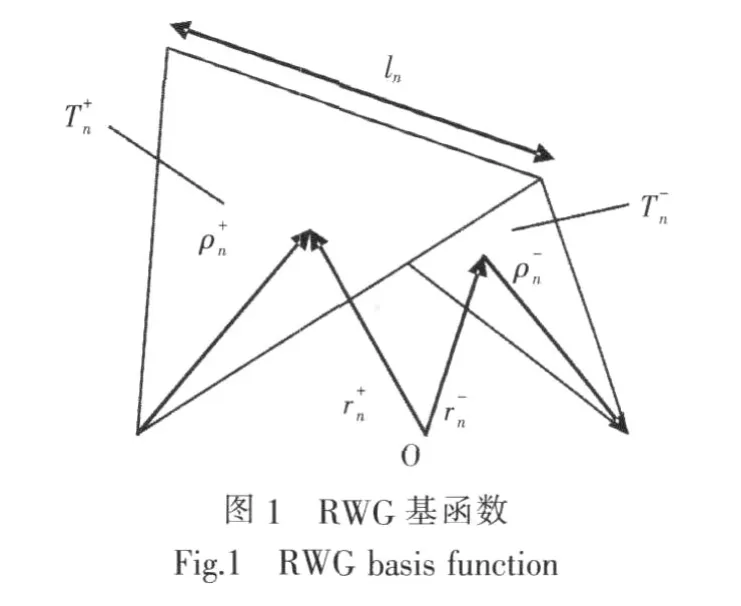
采用矩量法计算电场积分方程时，导体表面采用平面三角形面元进行剖分，基函数选择如图1所示的RWG基函数［9］，导体表面电流J可表示为：

其中，N为未知量总数；In为待求电流密度系数。用伽略金法检验后，按照矩量法的标准形式得到矩阵方程：

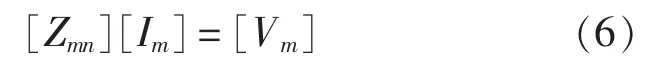
当确定［Zmn］和［Vm］后，可通过求解矩阵方程得到［Im］。结合电场积分方程，可得出Zmn和Vm的表达式如下［9］：

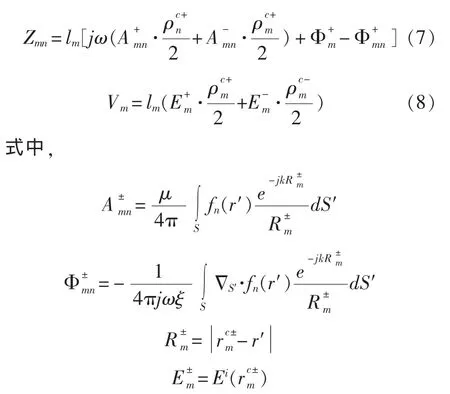
式（4）～式（8）中，r为场点坐标；r′为源点坐标；m、n对应于2个边元；r为边元m的2个三角T的中心点，分别是边元m的2个三角T的自由顶点到中心点的矢量。

2.2 电磁辐射理论分析

当我们考虑线天线的辐射模式时，激励源将由入射波变为电压源，需要将馈电模型引入天线结构以便考虑电压源的影响。在实际工程中，有多种方式设置激励源，其中较为常用的是由传输线通过两个靠近的端子馈电。对于这种激励模式，可以很好的用δ函数缝隙电压源模型进行模拟［10］。当用缝隙电压源激励时，假设缝隙宽度可以忽略不计，则缝隙内的电场可以用δ函数近似表示为：

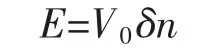
式中，V0为外加加压；n为电场方向。

将间隙与边元结构的内部边m联系起来，对应此内部边只有一个RWG边元m。除此边元以外，其他地方，入射场均为0。对于边元m上的激励电压，可通过下式给出：

而后，可通过式（6）计算得出［Im］。

2.3 细带模型建模

根据相关文献论述［11］，具有电小尺寸的圆柱线天线，当天线半径r远小于波长λ时，其电磁特性可用一条金属细带等效。天线半径与金属细带宽度之间的关系为r＝0.25 s。其中，r为天线的半径；s为金属细带的宽度。进行等效后，可通过建立一个金属细带模型代替圆柱线天线，并进行三角形网格剖分，用RWG函数描述金属细带上的电流分布。可以证明，每个边元的基函数可近似成长度为的有限小电偶极子。式中，rc±为边元的两个三角T±的中心点，RWG边元可以保证沿金属细带有均匀的轴向电流，满足细线理论的假设［10］。

2.4 电场磁场计算

建立金属细带模型后，要计算空间某点处的电场、磁场，可以通过计算每个边元对应的有效电偶极子在空间某点处的电场、磁场并进行求和，得出该点处的电场、磁场大小。位于原点的长度为d的有限小电偶极子在空间某点处R的辐射磁场和电场以矢量形式可以表示为［12］：

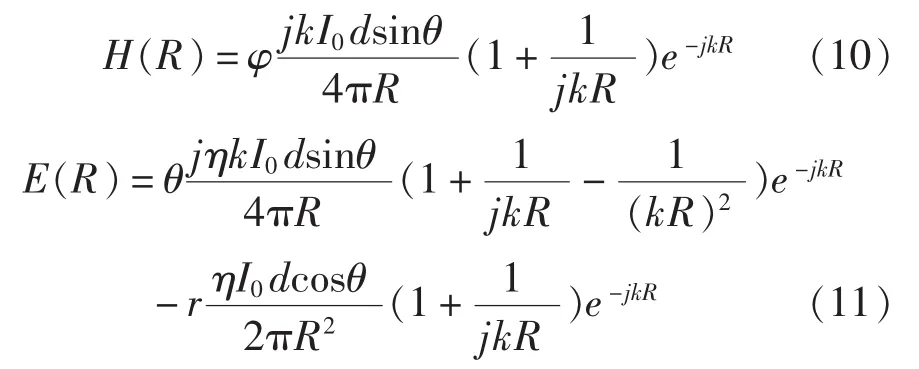
式中，r、θ、φ分别为球坐标系中的单位坐标。上述方程是精确表达式，没有进行远场近似，可以计算离开偶极子外任意点处的电场、磁场。但考虑到模型中等效的有效小电偶极子具有一定的长度，实际能计算的范围应该大于电偶极子长度的量级。如果要计算非常近的距离的电场、磁场强度，则需要在模型网格剖分时划分更细的网格，以满足计算精度的需求。

考虑各个边元的合成效果，则空间某点R处的电场和磁场为：

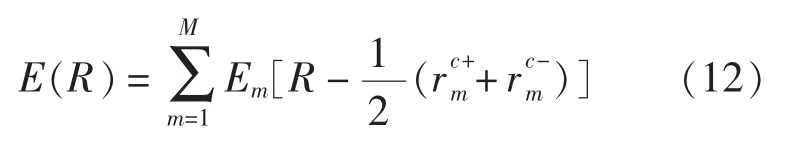
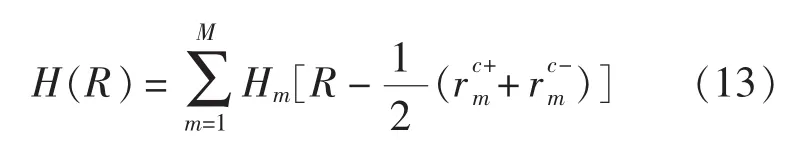
3 数值计算与分析

为了验证上述算法，分别进行了不同情况下的偶极子天线的散射仿真，辐射仿真和单极子天线的辐射仿真。首先在MATLAB环境下生成均匀网格化的天线模型。可以通过编写程序，定义天线和平板的长、宽、剖分密度，生成网格时，使用德洛内三角化［10］。实际工作中可以很方便的生成任意长、任意宽的三角化天线网格，通过控制剖分密度达到控制未知量的数目，满足计算精度和计算速度的要求，具有广泛的适用性。

3.1 偶极子天线散射模型仿真

仿真频率设置为50 MHz，偶极子半径分别设置为波长的 10－5、10－4、10－3、10－2， 等效细带宽度分别为波长的4 × 10－5、4 × 10－4、4 × 10－3、4 × 10－2，细带长度为3 m。入射信号是垂直于细带模型平面的平面波，该平面波只有沿细带轴向方向的电场分量，大小为1 V／m。分别得到细带模型的表面电流强度分布，辐射电场强度和方向性图如图2所示。

在图2中可以看出，随着天线半径的增加，表面电流强度分布逐渐减小，这是因为在其等效金属细带模型中，随着天线半径的增加，金属细带的宽度逐渐增加，表面电流在横向方向上的分量逐步增大。从图3和图4中可以看出天线半径的变化对于电场和方向性的变化影响较小。

3.2 偶极子天线辐射仿真

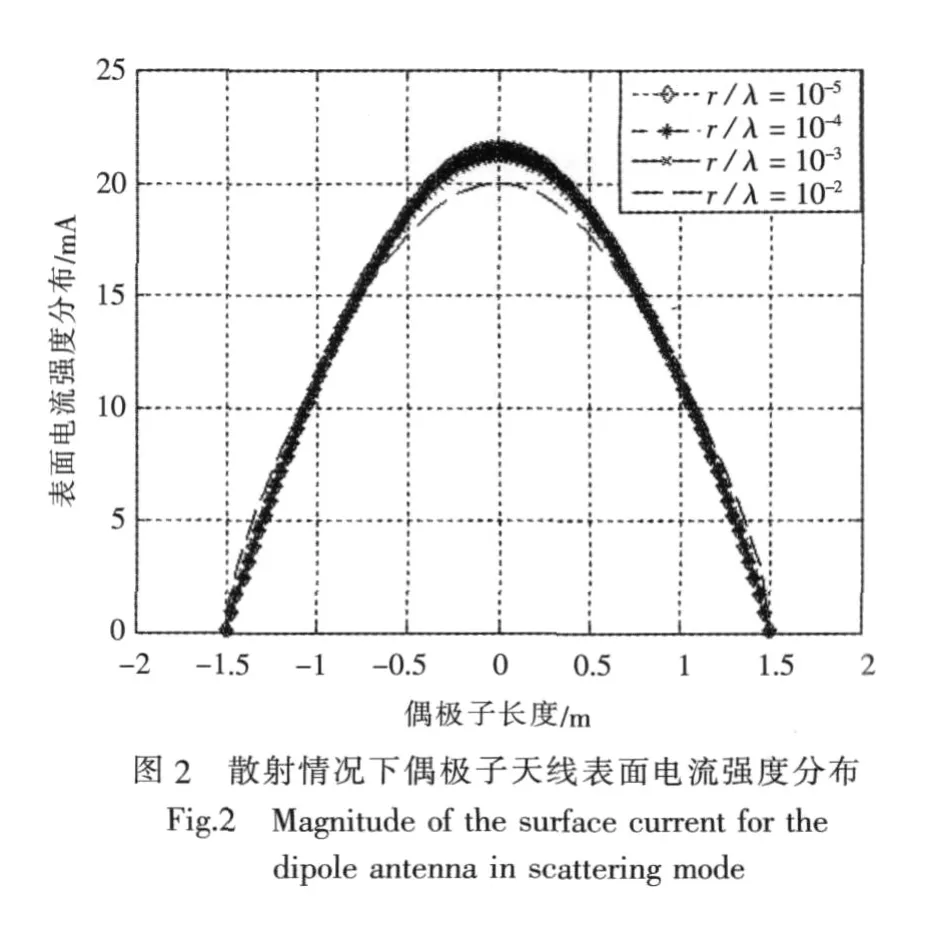
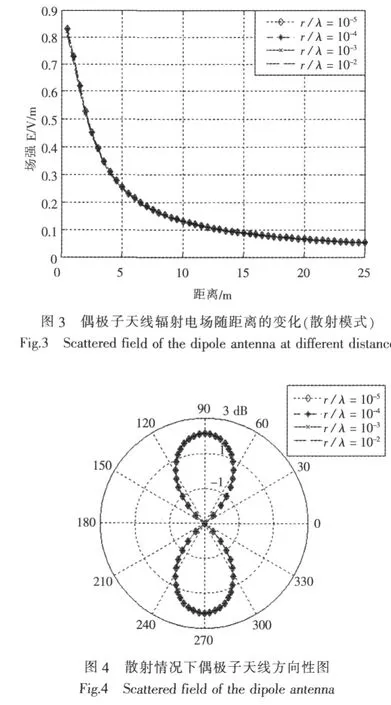
偶极子天线模型采用3.1节中所采用的模型，激励信号由入射平面波改为馈电电压为1V的电压信号，馈电点位于天线中点，分别得到细带模型的表面电流强度分布，辐射电场强度和方向性图如图5所示。

从图5中可以看出，当天线半径较小时，细带模型上的电流分布基本呈现正弦分布，这是因为天线半径较小时，天线上的电流基本沿轴向流动。随着天线半径的增大，当半径与波长的比值为0.01时，细带模型上的电流分布已不在呈现正弦分布，究其原因是此时的电流分布已不能近似为沿轴向分布，横向方向上的电流分布增大所致。这种情况与前面表述的偶极子天线电磁散射的情况有所不同，在电磁散射情况下，当半径与波长的比值等于0.01时，虽然电流的幅度有较明显的变化，但仍然呈现正弦分布。这两者不同的原因在于，在散射环境下，整个金属细带上的电流分布更加平均，对细带宽度的要求比辐射情况下更低。所以在进行天线辐射仿真时，应注意金属带宽度与长度的比值不能过小。

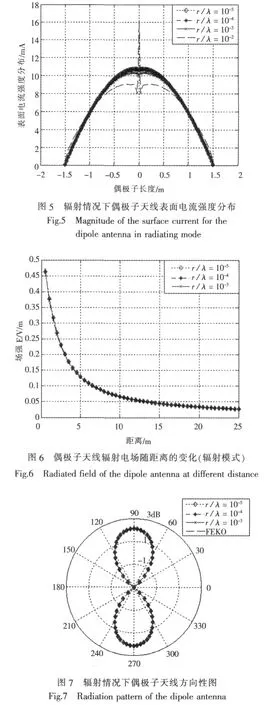
在图6、图7中，我们舍弃半径与波长的比值等于0.01的情况，分别计算了辐射电场从近场到远场的变化以及方向性图。在图7中，引入在FEKO中仿真进行的偶极子天线的方向性图作为比较依据。可以看出，在三种情况下，电场分布数据的吻合度都很高，只有细微的差别。方向性图的吻合度也很高，并且与在FEKO中的仿真结果极为相似，验证了这种算法的准确性。

3.3 单极子天线辐射仿真

10 m鞭天线是舰船上常用的通信天线，属于单级子天线，通常有2根天线分别布置于上层甲板的左右舷。分析10 m单级子天线的本身特性和组合布置情况下的特性具有重要的实际意义。本文分别仿真了两种情况下的单极子天线，第一种情况是置于20×20 m的平板中心的一根长为10 m的单极子天线，底部馈电。第二种情况是在20×20 m的平板上分别放置两个单极子天线，位置分别位于平面中心的左侧7.5 m处和右侧7.5 m处，对左侧的单极子天线底部馈电，右侧的单极子天线不馈电，馈电电压设置为300 V，模型如图8所示。

常用的10 m单极子天线的工作频率为5～28 MHz，计算10 m单极子天线的输入阻抗如图9所示。

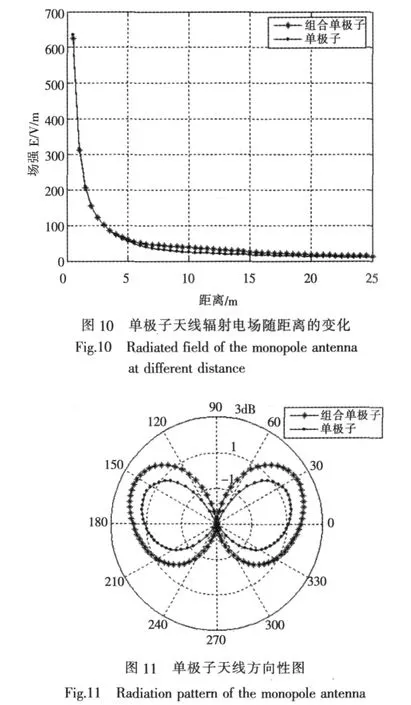
表1比较了两种模型在7.5 MHz时的输入阻抗和增益值，可以看出，组合单极子模型的增益更大，输入阻抗的实部增大。图10所示为两种模型在7.5 MHz时的辐射电场从近场到远场的变化关系，可以看出两者的辐射电场有细微的差距，随着距离的增加，两条曲线逐渐重合。图11给出了两种模型的方向性图，从图中可以明显的看出组合单极子的增益更大，方向性更强。

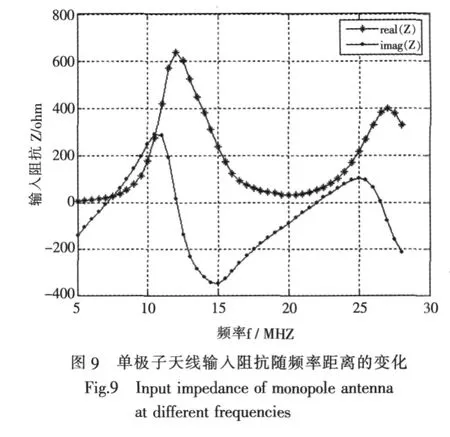
表1 7.5 MHz时2个模型的比较Tab.1 Comparison of the two models at 7.5 MHz

4 结论

基于矩量法，采用RWG基函数对3 m长偶极子天线和有限平板上的10 m长单极子天线的特性进行了分析。分析偶极子天线的半径发生变化时，其散射和辐射模式下的表面电流强度分布，场强分布和方向性图，并与FEKO中的方向性图试验结果进行比较，证明了这种方法的正确性。随后进行了单极子天线和组合单极子天线的特性比较，为实际工程中的仿真计算提供有效的参考依据。

［1］HARRINGTON R F.Field Computation by Moment Methods［M］.New York： Macmillan，1968.

［2］阙肖峰，聂在平，宗显政.复杂金属载体上线天线的MoM分析［J］.微波学报，2006，22（5）：16－20，38

［3］梁荣江.基于Matlab分析矩量法在线天线中的应用［J］.西安邮电学院学报，2009.14（1）：49－52，56

［4］MAKAROV S.MoM antenna simulations with MATLAB：RWG basis functions ［J］.IEEE Antennas and Propagation Magazine，2001，43（5）：100－107.

［5］张云华.用基于rao－wilton－glisson基函数的矩量法分析线天线 ［J］.系统工程与电子技术，2005，27 （6）：1105－1108.

［6］董健，柴舜连，毛钧杰.任意形状线、面、体组成导体目标的电磁建模［J］.电子学报，2005，33（9）：1656－1659.

［7］芮翔，徐忠伟，程嗣怡.基于RWG基函数的平面螺旋天线建模及仿真研究［J］.现代防御技术，2009，37（4）：109－113.

［8］廖艳苹，杨莘元，马惠珠，侯艳丽.有限偶极子天线阵的电磁散射理论研究［J］.兵工学报，2007，28（2）：182－186.

［9］RAO S M，WILTON D R，Glisson A W.Electromagnetic Scattering by Surfaces of Arbitrary Shape ［J］.IEEE Trans Antennas and Propagation，1982，30（3）：409－418.

［10］MAKAROV S N.通信天线建模与MATLAB仿真分析.许献国，译［M］.北京：北京邮电大学出版社，2006.

［11］JOHN L V.Antenna engineering handbook，fourth edition［M］.New York：McGraw－Hill，2007.

［12］BALANIS C A.Antenna theory：analysis and design，third edition［M］.New York：Wiley，2005.

Analysis on the Electromagnetic Scattering and Radiation of Wire Antenna by Moment Method

Gao Bao-chun Peng Ge Hu Yi-feng
China Ship Development and Design Center， Shanghai Division，Shanghai 201108，China

Analytical method was chosen to describe the structure of wire antenna.The wire antenna was modeled as a thin strip， wire－surface junction problem was transformed to surface－surface junction problem.RWG function was chosen to discretize the surface of antenna.Current distribution， radiation field and directivity of different radius dipole antennas were analyzed by using method of moment，and then the results of radiation pattern and scattering pattern were compared.The characteristics of 10m monopole antenna on the finite plate were calculated.The results show that： when the radius and or wavelength are small， the current flows along the antenna axial， the line current model is applicable to the problems of wire antennas， but when they are large， horizontal currents cannot be ignored， the line current model is unsuitable for the analysis of wire antenna problems.

method of moment； RWG basis function； wire antenna； electromagnetic scattering； electromagnetic radiation

U674.7

A

1673－3185（2011）03－49－06

10.3969/j.issn.1673-3185.2011.03.011

2010-09-03

“十一·五”海军装备预先研究项目（40******101）；“十一·五”海军武器装备研制项目（09***／***3）

高宝春（1987－），男，硕士研究生。研究方向：舰船电磁兼容，计算电磁学。E-mail：gaobaochun＠yahoo.cn