采用互补滤波器组进行频带分解的欠定盲源分离方法
2011-03-05朱立东
冯 涛,朱立东
(电子科技大学通信抗干扰技术国家级重点实验室,成都 611731)
1 引 言
盲源分离(Blind Source Separation,BSS)是指在不知道源信号和传输通道的参数情况下,根据输入源信号的统计特性,仅用观测信号恢复出源信号的过程。欠定情况下的盲源分离是一个更符合实际情况也更具有挑战性的问题。由于欠定情况下系统是不可逆的,即使混合矩阵已知,源信号也不存在唯一解。在解决欠定盲源分离问题的主要方法中,基于信号稀疏性表达的算法适用范围相对较广,被当前大部分的欠定盲源分离算法所采用。信号在时域的稀疏性常常很难满足,目前,算法为了达到稀疏性一般采用变换域的方法,如小波变换或者短时傅里叶变换。Yilmaz等人假设源信号在时频域上是相互非重叠的,即在每一个时频点上仅允许一路信号存在[1];Aissa-El-Bey等人将上述条件进行了放宽,要求在任意时频点上的信号数严格小于观测信号数[2]。上述分离方法对语音信号具有良好的分离性能。但时频分析对瞬时频率的估计存在时间精度与频率精度的根本矛盾,所以对复杂信号,特别是瞬时带宽比较大的信号,估计性能会明显下降。
通过分析现实中的信号(特别是无线通信信号)可以发现,这些信号往往是带限信号。虽然源信号数大于观测信号数,但在一些子频带上,源信号数并不大于观测信号数,所以在这些子频带上可以采用经典的ICA算法进行分离。当每一个子频带都满足源信号数不大于观测信号数的条件时,就可以通过把同一个信号在不同子频带的分离结果进行叠加进而有效地恢复出每一路源信号。由此可见,当条件改变为每一个子频带的源信号数不超过观测信号数时,欠定盲源分离在理论上是可行的。本文假设在每一个子频带源信号数量不大于观测信号数量,以此为基础,解决欠定盲源分离问题。
经互补滤波器分解后的信号可以通过简单的叠加得到恢复,信号重构过程简单且准确度高;同时,相对时频分析的方法而言,滤波器可以对信号频谱划分较随意,相邻频带间的隔离度很好,所以本文采用互补滤波器组对观测信号进行子频带分解。
本文的结构组织如下:第二部分介绍欠定盲源分离的基本模型及后面将用到的基本知识;第三部分重点阐述本文提出的基于互补滤波器组的欠定盲源分离方法,其中也提出了新的混合矩阵的估计方法;第四部分是通过仿真验证该方法的可行性并进行性能分析;最后一部分进行总结。
2 系统模型及基础理论
2.1 系统模型及基本假设
设M维观测信号矢量用x(t)=[x1(t),x2(t),…,xM(t)]T表示,N维信源矢量为s(t)=[s1(t),s2(t),…,sN(t)]T,则可得线性瞬时混合系统的数学模型:

式中,A∈RM×N(M 在以上的盲源分离问题中,由于源信号和混合系统均未知,如果没有任何其它先验知识,要想仅从观测信号恢复出源信号是极其困难的。所以,为使问题可解,根据实际存在情况作以下基本假设: (1)源信号为带通信号,源信号数已知且通过子频带划分可以满足每一个子频带的源信号数量不超过观测信号数; (2)混合矩阵A非奇异且其中任意M列组成的方阵为满秩矩阵; (3)源信号 s(t)为零均值随机矢量,在任一时间点,源信号各分量之间是相互统计独立的; (4)由于高斯信号的线性相加仍是高斯的,不可能被分开,所以假设信源中最多只有一个高斯分布。 定义1:一组滤波器H1(z),H2(z),…,HL(z),如果它们的转移函数满足: 式中,c为常数,称H1(z),H2(z),…,HL(z)是一组严格互补(Strictly Complementary,SC)的滤波器。 用这一组互补滤波器将信号s(n)分解为L个子带信号,然后再相加,则可得: cS(z)z-n0对应的时域信号为 cs(n-n0),和s(n)相比,它有一个延迟n0,并乘以一个常数c。显然,用这种严格互补的滤波器组对信号s(n)做分解后,可以用分解所得到的信号来准确重建原来的信号。同时,可以得到如下定理: 定理 1:在盲源分离中,设源信号 s(t)=[s1(t),s2(t),…,sN(t)]T,混合矩阵 A=[a1,a2,…,aN],其中源信号sn(t)所对应的混合矩阵的列为an。位于互补滤波器组的第 l个子频带中的源信号为sl(t)=[sl1(t),sl2(t),…,slp(t)]T(p≤M),这些源信号所对应的混合矩阵中的列所组成的新矩阵为Al=[al1,al2,…,alp](p≤M),则对观测信号x(t)=[x1(t),x2(t),…,xM(t)]T经过滤波器 l的输出信号进行盲源分离后,得到的估计混合矩阵有 式中,Pl为一个置换矩阵。 由定理1可知,当观测信号通过互补滤波器组的每一个滤波器后,如果输出信号包含的叠加源信号数不超过观测信号数,即p≤M时,用传统的独立成分分析方法(如FastICA[4]、JADE[5])可以有效地分离出源信号的子频带信号,同时,由互补滤波器的良好信号重构能力,只要把同一源信号在不同频带的分离信号按同一放缩比进行叠加,就可以有效地恢复出源信号。 在本文提出的方法中,互补滤波器对分离性能存在影响。在假设1满足的条件下,困难在于如何找到这样一个互补滤波器组满足每一个滤波器包含子频带的信号数不超过观测信号数。可以采用逐步细化的方法,先检测在每一个大的子频带的信号数是否超过观测信号数,子频带的信号数检测方法可以采用常用的欠定盲源信号数估计方法[6],如果超过,则将该子频带再细化,直到满足滤波器划分的每一个子频带的信号数不超过检测信号数的要求。 为了取得优良的估计性能,在互补滤波器的设计中同时应注意以下两个方面: (1)为了充分的划分频带,互补滤波器组的每一个滤波器的通带到阻带间过渡频段应尽可能窄,以减少非该子频带源信号的干扰; (2)互补滤波器的严格互补往往很难达到,所以在设计时要求滤波器组尽量严格互补,建议在设计时采用等阶数的有限冲激响应(Finite Impulse Response,FIR)滤波器组。 在完成滤波器设计后,将观测信号分别通过滤波器组,可以得到在每一个子频带的观测信号,由假设2,我们可以在每一个子频带分别采用常规的独立成分分析方法,得到每一个子频带的混合矩阵。 (1)通过互补滤波器组将观测信号分离到L个子频带,得到L个观测信号矩阵x1(t),…,xl(t),…,xL(t); (2)对每一个观测信号矩阵首先进行主成分分析[7](Principle Component Analysis,PCA),抑制噪声及其它源信号对该子频带的干扰,然后通过独立成分分析得到估计混合矩阵 并将每一个向量转化为空间方向向量, 上述的混合矩阵估计方法,因为在聚类分析前已通过独立成分分析的方法对混合矩阵列向量进行了前期的估计,所以聚类分析的每个样本值都是对原混合矩阵列向量的较好估计,因此总的估计性能较优秀。 与基于时频域的盲反卷积方法类似,基于互补滤波器组的欠定盲源分离方法也存在排列模糊的问题。因为混合矩阵的列向量与源信号存在一一对应关系,解决了各子频带估计混合矩阵的排列模糊问题,也就解决了各子频带估计分离子信号的排列模糊问题。 当采用算法1以外的其它算法进行混合矩阵估计时,因为 A是对A的估计, Al是对Al的估计,而Al是由A的一部分列所组成的子矩阵,所以可以简单地通过将中的列向量分别与 A中的列向量做内积,内积最大的列就是相互对应的列,注意在求内积前应先将及的列归一化。解决了与中列的对应关系,也就解决了排列模糊的问题。 如采用上一节的算法1进行混合矩阵估计,则在利用聚类分析算法估计混合矩阵的同时,也判定了每一子频带所包含的信号归属。利用估计的混合矩阵,再重新求解出独立的子频带信号。 然后把同一路源信号的不同子频带分离信号相叠加即可得到源信号的估计。具体算法(算法2)流程如下: (1)利用算法1估计混合矩阵,解决排列模糊问题,确定每一个子频带所包含信号归属; (2)利用式(6)恢复每一个子频带中的独立子信号; (3)将第1步解决的信号归属问题与第2步得到的独立子信号相结合,将归属于同一源信号的不同子频带的分离子信号叠加恢复源信号。 考虑源信号为四路相互独立的带限源信号,频率都在0~8 kHz内,经2 s 16 kHz采样。其中,信号1为语音信号,频率位于整个频带(0~8 kHz);信号2为频率为30Hz的正弦信号;信号3为载波为3 kHz的BPSK信号,频率主要位于2~5 kHz;信号4为载波为7 kHz的FSK信号,频率主要位于6.7~8.0kHz,可以看出,四路源信号的频率都没有独立存在,但在每一个频率点,其主要信号成分只由两路构成。 当观测信号为两路时,通过滤波器设计,可以通过3个滤波器完成盲分离(3个滤波器通带分别为0~1 kHz,1~5.2 kHz,5.2~8 kHz),这里采用的互补滤波器组为阶数为300阶的FIR滤波器。另外,观测信号数的增加也可以有效减少滤波器数量,进而减小重构误差及错误重构的概率。 原混合矩阵及由算法1得到的估计矩阵分别为 可以看出,算法1对于混合矩阵的估计性能是很优异的。在估计出混合矩阵后,我们可以通过算法2恢复出源信号。这里我们将本文提出的算法与文献[2]中提出的基于时频域的经典欠定盲源分离算法做一对比,考虑在不同信噪比下的分离性能。为了更准确地对两种源信号估计算法进行比较,这里考虑在进行分离前,混合矩阵都已知准确地进行了估计。我们采用均方误差作为判断标准,均方误差的定义如下式: 式中,R是总的仿真次数(R=100),M为总的源信号数,N为源信号的样本数,Λr为一个对角矩阵,Pr为一个置换矩阵, smr(n)是第 r次仿真中对样本sm(n)的估计。 在仿真过程中,混合矩阵A为随机产生,A中的元素服从-1到1的均匀分布。分离性能对比如图1所示,图中给出了不同信噪比下算法2在两路观测信号时的性能,并且给出了时频域方法在三路观测信号时的分离性能。由图可以看出,本文提出的方法在各信噪比下都取得了比时频域方法更好的分离性能。 图1 两种欠定盲源分离算法的性能对比Fig.1 Comparison between the two under-determined BSS algorithms 本文针对欠定盲源分离问题,结合常见源信号为带限信号的特点,提出了采用互补滤波器组进行时域分解的欠定盲源分离方法。与当前常见时频域方法相比,将对信号时频域稀疏性的要求转化为对信号频域稀疏性的要求,相对而言要求有所提高,但可以进行欠定分离的信号数增加了一路。因为对所有子频带的信号进行联合估计混合矩阵,可以更有效地抑制噪声对信号恢复的影响,对混合矩阵的估计及对源信号的恢复效果都更好。本文的方法虽然是基于频域的考虑,但整个过程都在时域进行,避免了时频域的转化,可以有效提高运算效率。在后续的工作中,应该进一步增强算法的鲁棒性,考虑滤波器的有效设计问题并将算法与实际信号相结合。 [1]Yilmaz O,Rickard S.Blind separation of speech mixtures via time-frequency masking[J].IEEE Transactions on Signal Processing,2004,52(7):1830-1847. [2]Aissa-El-Bey A,Linh-Trung N,Abed-Meraim K,et al.Under determined blind source separation of nondisjoint sources in time-frequency domain[J].IEEE Transactions on Signal Processing,2007,55(3):897-907. [3]Peng Qi-chong,Shao Huai-zhong,Li Ming-qi.Signal Analysis[M].Beijing:Publishing House of Electronics Industry,2006:218-221. [4]Hyvarinen A,Oja E.A fast fixed-point algorithm for independent component analysis[J].Neural Computation,1997,9(7):1483-1492. [5]Cardoso JF,Souloumiac A.Blindbean forming for non Gaussian signals[J].IEEE Transactionson Radar and Signal Processing,1993,140(6):362-370. [6]Lieven De Lathauser,Josephine Castaing.Blind Identification of Under determined Mixtures by Simultaneous Matrix Diagonalization[J].IEEE Transactions on Signal Processing,2008,56(3):1096-1105. [7]Jolliffe I T.Principal Component Analysis[M].2nd ed.New York:Springer,1996:21-27.2.2 互补滤波器[3]
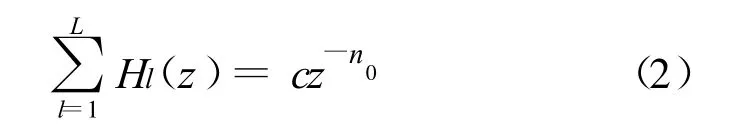


3 基于互补滤波器组的欠定盲源分离方法
3.1 互补滤波器设计
3.2 混合矩阵估计
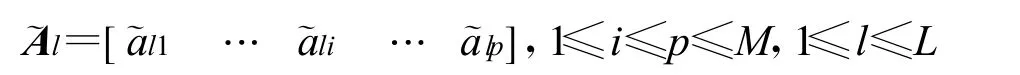


3.3 源信号恢复

4 仿真及性能分析



5 结束语
