电抗加载天线阵的优化设计及性能分析
2011-03-05李戈阳
李戈阳
中国舰船研究设计中心,湖北武汉 430064
电抗加载天线阵的优化设计及性能分析
李戈阳
中国舰船研究设计中心,湖北武汉 430064
为优化均匀圆形天线阵的辐射性能,利用矩量法对电抗加载偶极子均匀圆阵的波束形成进行了可行性分析,并设计了粗选与微扰结合的电抗加载值序列优化计算方法,以满足指定方向上波束形成的需求。仿真结果表明,电抗加载天线阵波束形成方法能有效在期望方向上形成具有较高增益与前后比的波束,且对阵半径与电抗加载值的误差具有一定的容错能力。该分析方法与计算结果对电抗加载天线阵的设计与实际工程应用具有一定的指导意义。
电抗加载;偶极子;波束形成;增益;前后比
1 引言
电抗加载天线阵以其结构简单,不需要多路接收机,采用对寄生振子进行电抗加载就可实现波束控制等诸多优点,在舰载通信系统[1-2]、现代雷达和通信[3]领域得到了广泛应用。利用寄生振子控制天线阵辐射方向的方法在本世纪初由日本学者提出,利用此方法制成的Yagi-Uda天线已在通信和广播等领域得到广泛应用,但将这一方法上升到理论高度的却是美国学者Harrington。1978年,Harrington首次提出电抗加载天线阵理论[4],并以七元圆阵为例对增益方向图进行了综合优化,用计算结果证明了理论的有效性。
基于电抗加载天线阵的基本理论,本文设计了小型均匀圆阵,并计算了天线阵半径的变化与电抗加载值的误差对天线阵电性能的影响。
2 电抗加载天线阵的分析与设计
2.1 电抗加载原理的矩量法分析
自从1978年Harrington将矩量法应用于电磁学后,矩量法一直是分析线天线辐射与散射问题的有效工具[5]。矩量法是一种将线性空间的算子方程转化为矩阵方程来进行计算的数值方法。本文根据矩量法原理,采用分段正弦基和伽辽金法计算了天线阵各单元的电流分布[6]。
根据矩量法原理,采用分段正弦基和伽辽金法分析天线。设每根振子均匀分为m+1小段,形成m个元偶极子,振子的全长为2L,共有n根振子。在第1根振子的中心,用电压源V0馈电。可构造矩阵方程:

在上式中,N=m×n。令加载的阻抗矩阵为[ZL],即
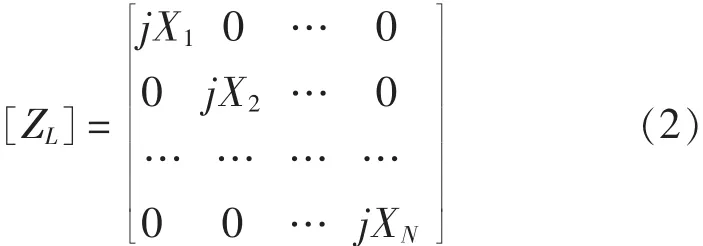
在矩阵[ZL]中,对角线上的元素为各天线的加载电抗值。考虑电抗加载后,新的广义阻抗矩阵[7]为:
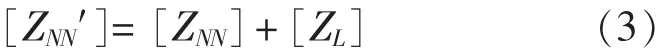
求解式(1),即可得各振子上的电流分布:
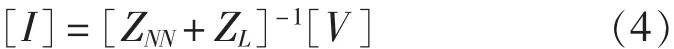
得到每个振子上的电流分布后,即可计算圆阵的基本辐射性能。
以上分析表明,通过改变天线阵中任一振子的电抗加载值,即可改变天线阵中各振子的电流分布,从而改变天线阵的整体辐射特性[8]。因此,可以考虑采用调整电抗加载值的方法,尽可能地增加天线阵在期望方向的增益,抑止旁瓣和压缩波束[9]等。以下将就加载电抗值序列的计算方法进行分析。
2.2 加载电抗值序列的分析计算
对于所研究的电抗加载天线阵,本文分以下两步对电抗加载值进行优化计算。
步骤一:加载电抗数值序列的有界粗选。
加载的电抗值必须易于用电感元件或电容元件实现,这是对优化结果最基本的要求。所以,在优化中,加载电抗值只能在一个有限的区间内变化[10],如果初值选取得当,还可大大缩短寻优时间[11]。从工程应用角度出发,本文将每根天线加载电抗值的取值范围设定为(-350,350)Ω,取50 Ω为步长,采用穷举法来计算期望方向上增益达到最大值时的加载电抗值序列。
步骤二:加载电抗值序列的微扰算法优化。
为使天线阵在期望方向上的增益G(θ,φ)尽可能增大,且对旁瓣进行抑止,本文利用微扰的方法对加载电抗值序列进行了优化,以尽可能避免计算结果陷入局部最优解。为便于描述,设主瓣的峰值增益为Gmax,第一副瓣的峰值增益为Gsec。
计算初值加载序列的G(θ,φ)、Gmax、Gsec,然后在初值加载序列基础上进行扰动,计算天线阵辐射特性,得到当前增益值G′(θ,φ)、G′max、G′sec。
1)当G′(θ,φ)≠G′max时:
(1)若G(θ,φ)=Gmax,则增强扰动,重新计算;
(2)若G(θ,φ)≠Gmax,且G′(θ,φ)/G′max≤G(θ,φ)/Gmax,则增强扰动,重新计算;
(3)若G(θ,φ)≠Gmax,且G′(θ,φ)/G′max>G(θ,φ)/Gmax,则接受该组加载值,将G(θ,φ)、Gmax、Gsec替换为G′(θ,φ)、G′max、G′sec。
2)当G′(θ,φ)=G′max时:
(1)若G(θ,φ)=Gmax,G′(θ,φ)/G′sec≥G(θ,φ)/Gsec,且G′(θ,φ)>G(θ,φ),则接受该组加载值,将G(θ,φ)、Gmax、Gsec替换为G′(θ,φ)、G′max、G′sec;
(2)若G(θ,φ)=Gmax,G′(θ,φ)/G′sec≥G(θ,φ)/Gsec,且G′(θ,φ)≤G(θ,φ),则以概率P1接受该组加载值,将G(θ,φ)、Gmax、Gsec替换为G′(θ,φ)、G′max、G′sec;
(3)若G(θ,φ)=Gmax,G′(θ,φ)/G′sec<G(θ,φ)/Gsec,且G′(θ,φ)>G(θ,φ),则以概率P2接受该组加载值,将G(θ,φ)、Gmax、Gsec替换为G′(θ,φ)、G′max、G′sec;
(4)若G(θ,φ)=Gmax,G′(θ,φ)/G′sec<G(θ,φ)/Gsec,且G′(θ,φ)≤G(θ,φ),则增强扰动,重新计算;
(5)若G(θ,φ)≠Gmax,则接受该组加载值,将G(θ,φ)、Gmax、Gsec替换为G′(θ,φ)、G′max、G′sec。
3)当连续增强扰动次数大于预设的容忍门限值T时,程序中止,输出加载值序列。
3 电抗加载天线阵的设计
其目标系统为电抗加载七单元圆阵,如图1所示。其中,天线单元为半波振子,工作中心频率12.5 MHz,振子半径10-3λ(2.4 cm),天线阵半径3/8λ(9 m),天线高度6 m。在电抗加载值序列的优化选择算法中,设期望方向为30°,接受概率P1=40%,P2=80%,容忍门限T=20,可计算得出各天线的加载值序列为[0-114.80-126.88 112.63-22.37-13.28 119.88],其从左至右依次对应于图1中编号1~7的天线单元所需加载的电抗值。
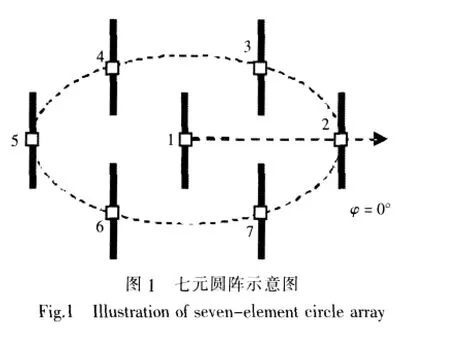
利用此组加载值,将天线的工作频率改变为12 MHz和13 MHz,分别进行计算,得到天线阵的输入阻抗、驻波比和增益如表1所示。
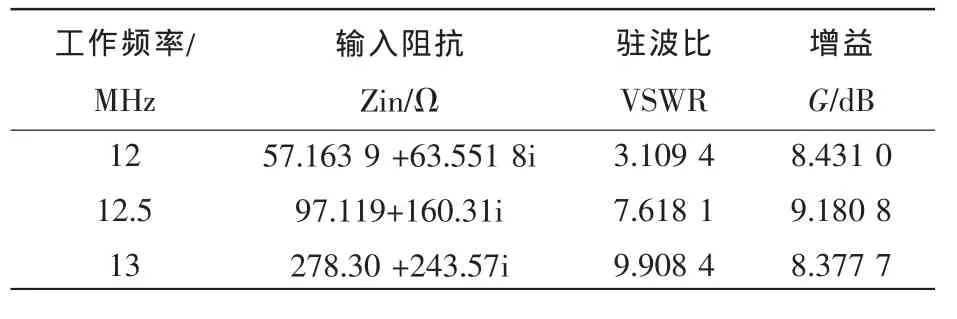
表1 天线电参数随工作频率的变化Tab.1 Variation of antenna electrical parameters along with operational frequency
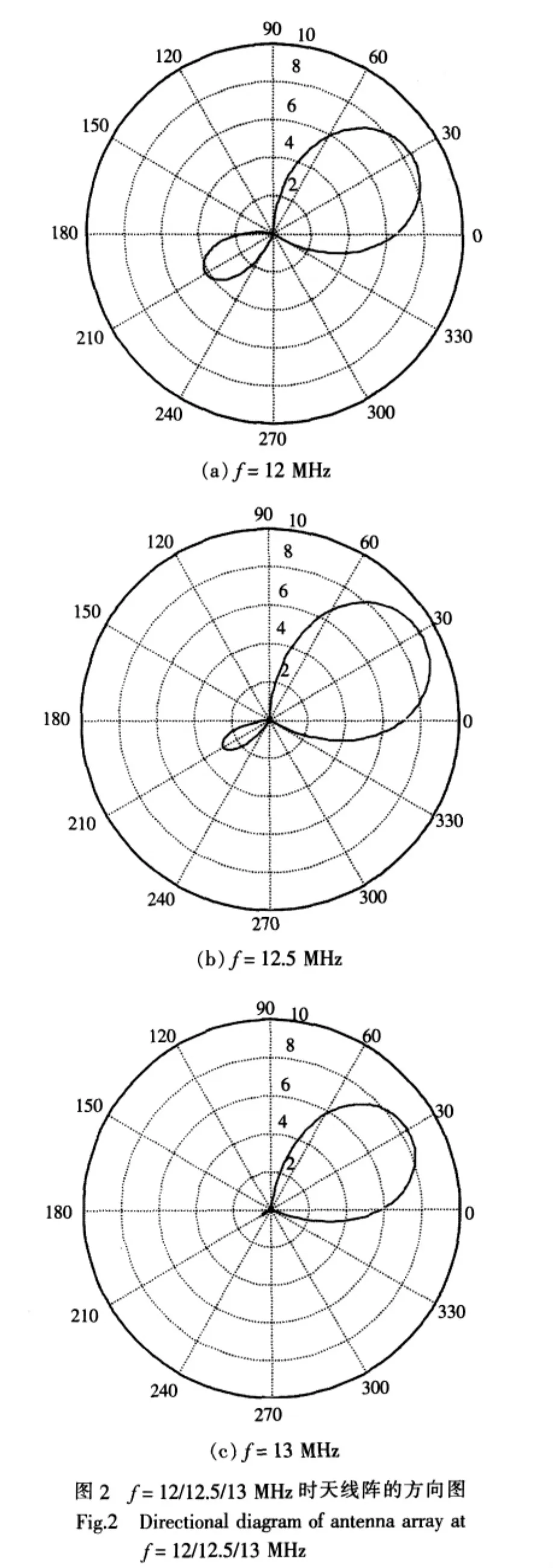
天线阵的E面(φ=0°)方向图如图2所示。
结合表1与图2可看出,当天线阵工作在中心频率12.5 MHz时,天线阵增益达到最大值9.180 8 dB,且较好地抑止了旁瓣。实验结果验证了方法的正确性,同时,还证明了该天线阵具有较好的方向性与增益。
当天线阵在12~13 MHz频带内工作时,方向图能较准确地对准期望的方向,且具有8 dB以上的增益,这说明该天线阵具有一定的带宽。对照表1与图2可看出,当天线阵的实际工作频率偏离中心频率时,主波束略偏离期望方向且主瓣增益有所降低。但此时,如图2a所示,天线阵方向图虽具有一定的后瓣,但驻波比比较理想,在对后瓣无严格限制要求时,可将其作为发射天线阵使用;如图2c所示,天线阵虽具有非常理想的旁瓣抑止效果,但驻波比偏高,在实际工程应用中,可考虑采用对天线加载优化匹配网络的方法来改善驻波比,使之降低到工程要求的范围内。
4 电抗加载天线阵性能影响因素分析
天线阵波束形成方法的性能是指天线阵参数的变化对方向图的影响,影响越小,天线阵的性能便越好,天线阵工作也越稳定。影响天线阵波束形成方法性能的因素有很多,例如,工作频率的变化、振子粗细的变化、振子长短的变化、天线阵半径的变化、加载电抗值的变化等。下面本文将以图1的七元圆阵为例来分析天线阵半径的变化和电抗加载值的变化对天线阵性能的影响。
1)天线阵半径的改变对方向图的影响。
研究对象为电抗加载七单元均匀圆阵 (图1),其天线阵参数设置为:工作中心频率f=12 MHz(工作波长λ为25 m),振子半径10-3λ(2.5 cm),天线高度1/4λ(6.25 m),天线阵半径3/8λ(9.375 m)。在电抗加载值序列的优化选择算法中,设期望方向为30°,接受概率P1=40%,P2= 80%,容忍门限T=20,计算此时的电抗加载序列值,并讨论天线阵半径变为 1/2λ、1/8λ、1/10λ时,其主波束指向与增益的波动。
实验结果如图3所示。在图中,给出了以dB数表示的天线阵增益值。
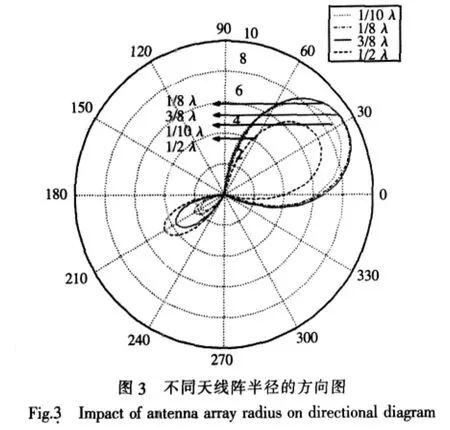
从图3中可看出,当天线阵的半径在1/2λ至1/10λ之间变化时,天线阵方向图的主波束始终能较准确地指向期望的30°方向,增益保持在7~9 dB之间,天线阵的辐射性能基本保持稳定。从工程应用角度出发,当安装环境不能满足设计要求时,可根据现场情况与系统对辐射性能的要求,在一定范围内对阵半径进行适应性调节,以满足工程应用需要。
2)电抗加载值的误差对方向图的影响。
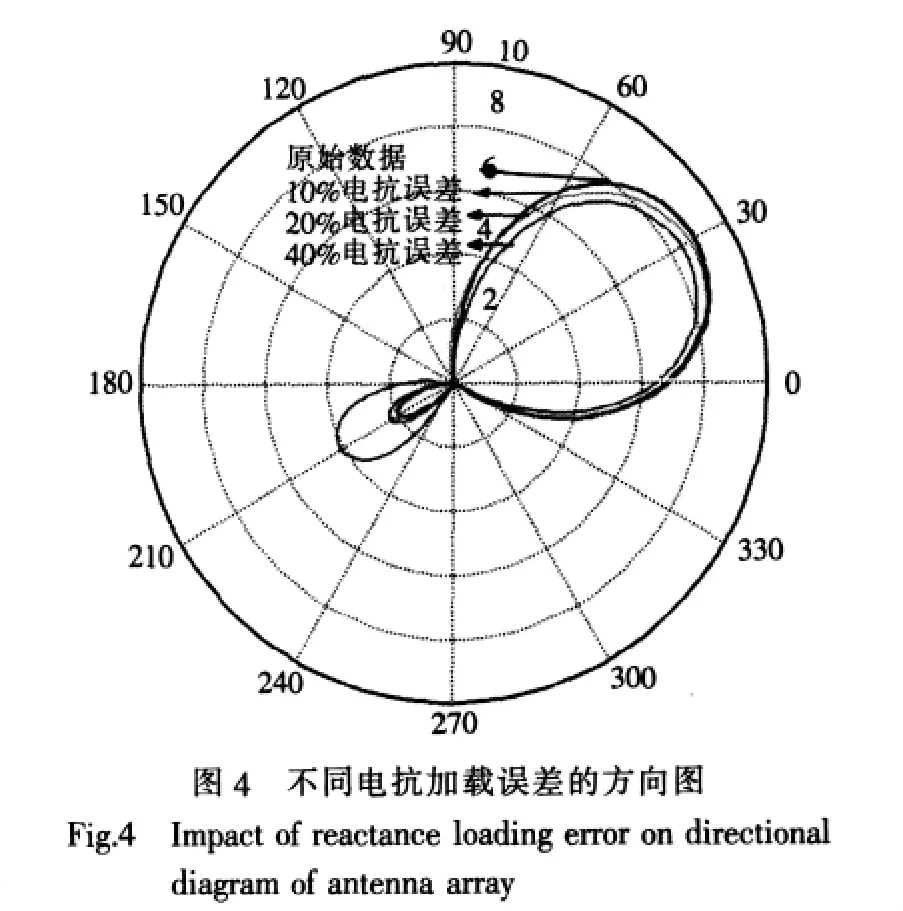
研究对象仍为上例中的天线阵。图4中原始数据对应的方向图与图3中阵半径为3/8λ时的方向图相同,该方向图是根据优化计算所得的电抗加载值序列所产生的。
在本节的性能分析中,分别对优化计算所得电抗加载值产生了10%、20%和40%的随机扰动,并得到了3组加载值,然后分别利用这3组加载值序列计算了天线阵方向图,仿真结果如图4所示。
从图4可看出,天线阵的辐射性能,如增益、主波束宽度与指向、后瓣增益等指标,在加载电抗值发生偏差时基本能保持稳定,即使是在电抗加载值产生40%的误差时,天线阵方向图的主波束也基本能稳定在期望的30°方向,后瓣依然在可接受范围。在电抗加载值存在较小误差的情况下,如10%与20%,天线阵的性能未受到明显影响,这说明天线阵对加载电抗值的误差具有一定的容错能力。当将本方法应用于实际工程时,无需精确加载理论计算的电抗值,只需加载与计算的精确值相近的标称值即可达到预期结果。
5 结 论
本文以矩量法为基础,采用电抗加载的思想对对称振子均匀圆阵进行了分析计算。仿真结果表明,利用文中方法计算所得的电抗值对天线进行加载,能使天线阵在期望方向形成具有一定增益且后瓣较小的波束,对舰艇信息的定向、保密发送与接收具有一定的应用价值。其性能分析也验证了该天线阵对阵半径的误差与电抗加载值的误差具有一定的容忍能力,使其较易于工程实现与应用。当在舰艇上使用时,该型天线阵具有相对较大的占舰面积,因此,需要在确保波束宽度、增益、
波瓣前后比等性能的前提下,进行进一步的小型化设计,如对天线单元进行顶端加载以降低振子高度,将天线阵设计成非均匀阵或半圆阵等。
[1] 朱永建.舰载通信天线发展综述 [J].舰船电子工程,2008,168(6):15-17.
[2] 江小平.舰载通信系统及其关键技术研究[D].武汉:华中科技大学,2007.
[3] 周涛,孔庆国,钱一婧,等.高频地波雷达技术及其发展趋势[J].雷达与对抗,2008(4):1-5.
[4] HARRINGTON R F.Reactive Controlled Directive Array[J].IEEE Trans on Antennas and Propagation,1978,26(3):390-395.
[5] HARRINGTON R F.Field Computation by Moment Methods[M].New York:Macmillan,1968.
[6] HARRINGTON R F.计算电磁场的矩量法[M].王尔杰,译.北京:国防工业出版社,1981.
[7] 牛俊伟.电抗加载定向天线阵的辐射特性研究 [D].西安:西安电子科技大学,2001.
[8] 柳超,刘其中,梁玉军,等.舰用短波宽带鞭状天线研究[J].电波科学学报,2006,21(6):955-958.
[9] 胡航,刘伟会,吴群,等.一种有效的子阵级波束扫描旁瓣抑制方法[J].电波科学学报,2009,24(4):593-597,666.
[10] 韩明华,袁乃昌.基于整体退火遗传算法的不等间距天线阵的综合[J].现代雷达,1998,20(6):72-77.
[11] 祝志鹏,蒋凤仙,陈学峰.一种改进的遗传算法及其在线天线阵方向图综合中的应用[J].复旦学报(自然科学版),2001,40(1):55-60.
Optimization Design and Performance Analysis of Reactance Loaded Antenna Arrays
Li Ge-yang
China Ship Development and Design Center,Wuhan 430064,China
To optimize the radiation performance of circular antenna array,Method of Moments(MoM)was applied to analyze the feasibility of achieving beam forming by reactance loaded circular antenna array,which is consisted of symmetrically displaced dipole antennas.Then,coarse and turbulence combination searching algorithm for reactance loading sequence is proposed for beam forming in specified direction.The simulation results show that beams of relatively high gain and fore-rear ratio can be formed on required directions,and the errors of array radius and loaded reactance can be tolerated to a certain extent.The analysis methods and computational results are of certain significance to the design and practical engineering application of reactance loaded antenna array.
reactance loaded;dipole;beam forming;gain;fore-rear ratio
U665.26
A
1673-3185(2011)02-65-04
10.3969/j.issn.1673-3185.2011.02.013
2010-04-28
“十一五”预研基金资助项目
李戈阳(1982-),男,博士,工程师。研究方向:无线电物理。E-mail:ligeyang_82@163.com
