大跨度拱桥考虑几何缺陷的稳定性分析

朱克兆,易壮鹏

(1.长江勘测规划设计研究有限责任公司,湖北武汉 430010; 2.长沙理工大学土木与建筑学院,湖南长沙 410114)

0 引言

桥梁结构的稳定性是关系到安全和经济的主要问题之一,它与强度问题有着同等重要的意义,近年来随着桥梁跨度的日益加大和桥梁结构的日益复杂,稳定问题更为突出。桥梁的失稳破坏没有明显的征兆,带有很大的突然性,破坏是灾难性的,在桥梁工程设计中应该避免。

拱桥是以承受压力为主的结构体系,在过去的桥梁实践中也曾多次发生拱桥施工中失稳的事故,造成国家和人民生命财产的重大损失,拱桥的稳定安全性[1～4]是设计和施工中需要考虑的重要因素之一。大跨度拱桥存在几何缺陷时,即在制造、运输、安装以及运营等环节中拱肋轴线与理想线形存在偏离的情况下,拱肋在外荷载作用下将产生附加内力和变形,初始挠度将对拱桥产生不利影响。大跨拱桥考虑几何缺陷的稳定问题是极值点失稳,极限承载能力分析必须考虑大位移的影响,同时由于拱肋变形很大,应变和应力随之增加,线弹性本构关系不再适用,因此须同时考虑几何、材料非线性的影响。几何缺陷从分布的范围来看可以分为整体缺陷和局部分布[5]。整体缺陷在桥跨范围内沿拱肋均有分布,目前关于拱桥的整体缺陷的分析方法多采用一致缺陷模式法[3,4],实际工程中的几何缺陷分布具有很大的随机性[6,7],笔者采用随机缺陷模式法描述几何缺陷,并得到相关的分布方式。局部缺陷是指拱肋的某个部位存在局部的初始挠度,主要由节段的初始连接不当和局部损伤造成,它对稳定性的影响在目前已有文献中研究较少。

大跨拱桥考虑几何缺陷时其稳定性能必将受到影响,不同分布方式和大小的整体将使得拱桥的承载能力有一定程度的下降,局部缺陷所处的位置和大小对拱桥稳定性的影响目前尚不清楚。基于此,本章从拱桥的两类稳定问题出发,研究大跨度拱桥中几何非线性、材料非线性和初始几何缺陷对稳定性能的影响,探讨大跨拱桥在考虑各种几何缺陷时的屈曲特性和承载能力。

1 大跨度拱桥的稳定性理论

拱桥的稳定性分析有分支点失稳和极值点失稳两类受力性质根本不同的失稳形式,对应有线弹性屈曲分析和非线性极限承载能力分析两种求解方法。前者假定结构失稳时处于线弹性范围之内,结构内力与外荷载成比例关系,将稳定分析转化为求解特征值问题,得出的最小特征值就是临界稳定系数;后者则采用考虑了结构非线性的有限元法来求解大跨拱桥的稳定问题,它通过结构从加载开始到失稳全过程的响应,得出结构的荷载位移曲线,求解极限承载能力。线性屈曲分析概念清楚,计算简便,它可以预测拱结构屈曲的上限;非线性的极限承载能力分析则可以考虑结构的几何、材料非线性和几何缺陷等因素的影响,计算准确,精度高。由于这两类分析方法各自的优点以及两类稳定之间良好的相关性,本文采用这两种方法来分析大跨度拱桥考虑几何缺陷时的稳定性能。

UL列式下总体坐标系下结构的增量有限元平衡方程[8]为:

式中:

其中[tK0]和[tKσ]分别为结构的弹性刚度矩阵和几何刚度矩阵;{t+ΔtQ}为外荷载等效节点力向量;{tF}为单元应力的等效节点力向量;[tBL]和[tBNL]分别为格林应变的线性部分和非线性部分与位移的转换矩阵;[D]是材料矩阵;[tτ]和{tτΛ}分别为Cauchy应力矩阵和向量，这些元素都是对应时间t位形；tV是t时刻的体积。

1.1 线弹性屈曲分析

在式(1)中如果不考虑荷载项，且以初始荷载作用产生的单元内力来计算几何刚度矩阵，则有：

式中结构坐标系下的弹性刚度矩阵和几何刚度矩阵均在初始未变形的结构位置建立。拱结构存在分支失稳时,上式有非零解且结构有分支位移产生,其左端刚度矩阵的行列式必为零,即有:

由上式计算得到的最小特征值λmin即为临界荷载安全系数,这样结构的线弹性屈曲分析就转换成了求最小特征值问题。

1.2 非线性稳定分析

拱桥的非线性稳定分析可采用一定的计算方法直接对式(1)进行求解,得到结构从加载直至失稳的响应全过程,荷载-位移曲线上的最大荷载值就是结构的极限荷载。在求解过程中,若只考虑几何非线性因素,则得出弹性大位移稳定极限荷载,而同时考虑几何与材料非线性影响,就可求出结构的弹塑性大位移稳定极限荷载。大跨度拱桥考虑几何缺陷的极限荷载求解必须考虑非线性因素,本文分析拱桥的非线性稳定时分别计算弹性大位移和弹塑性大位移稳定承载能力,并进行对比分析。几何非线性分析通过UL列式基础上采用增量法和弧长法相结合进行迭代来实现,材料非线性则采用高斯积分法实现。

高斯积分法在单元的截面上和轴向取一定数量的高斯点,对每个高斯点根据其应力和应变状态进行数值积分,形成单元刚度矩阵,可方便计算结构的弹塑性刚度矩阵和等效节点力,用较少积分点达到较高精度。每个积分点的被积函数[Bi]T[D][Bi]按弹性或弹塑性计算,然后按全单元数值积分即可得到单元的弹塑性刚度矩阵[Kep],即:

其中ng是高斯积分的点数;分别为形函数和自然坐标与笛卡尔坐标之间的亚克比转换矩阵在高斯积分点的取值。

2 结构计算模型及几何缺陷的分布

2.1 结构计算模型

如图1-a所示的某下承式钢管混凝土系杆拱桥,主跨计算跨径为125 m,计算矢高为25m,桥面净宽25m;拱轴线为二次抛物线,拱肋采用哑铃形截面钢管混凝土,截面总高为2.6m,每个钢管外径为110 cm,钢管及腹板壁厚为2 cm,内充50号微膨胀混凝土;桥两侧各布置有8束27×Φj15(7φ5)高强钢丝作为系杆;吊杆间距为7m,上端锚固于拱肋顶部,下端锚固于横梁底;横梁、纵梁以及盖梁采用预应力混凝土结构,混凝土采用30号,桥面系和拱肋相交处设置端横梁;横撑由拱顶处1道X字形横撑和顺桥向每边2道横撑组成;桥面板采用高度为35 cm的预制空心板。

设计荷载标准为城-A级,人群3.5 kN/m2。在对下承式钢管混凝土系杆拱桥进行稳定性分析时,结构的自重荷载保持不变,横梁、纵梁以及横撑按实际截面输入;桥面系不按实际情况考虑,而是将桥面板、桥面铺装和桥面的活载视为均布线荷载施加在横梁上面。稳定性分析考虑的工况为恒载+桥面系的活载布置,非线性稳定分析通过不断加大桥面的活载布置使结构拱桥的主要承重结构达到极限荷载。

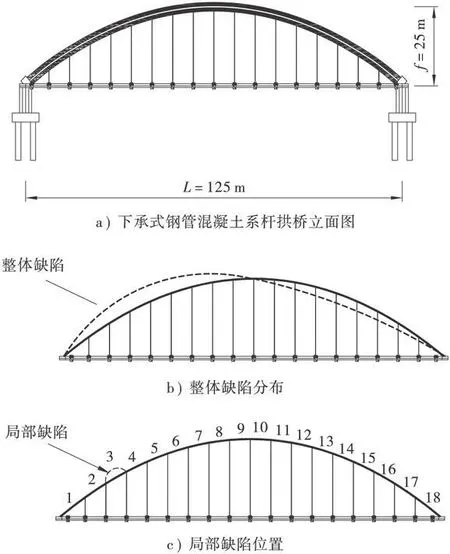
图1 下承式钢管混凝土系杆拱桥及几何缺陷

2.2 材料本构关系的选取

钢管混凝土的本构关系采用统一理论[9]考虑,将钢管混凝土视为钢管和混凝土组合而成的单一材料,其多线性随动强化的轴向应力—应变关系如图2所示。ξ和ξ0分别为钢管混凝土约束效应系数及其设计值,ξ=Asfv/Acfc,其中As,Ac分别为截面中钢材与混凝土面积;fv和fc分别为钢材屈服强度和混凝土抗压强度设计值。当ξ≥ξ0时曲线分为弹性(OA)、弹塑性(AB)与强化(BC)3个阶段;而在ξ＜ξ0时,曲线可分为弹性(OA)、弹塑性(AB)、强化(BC′)与下降(C′D)4个阶段。图2中弹性模量、强度及应变指标由以下各式确定。

钢管混凝土轴压组合强度标准值fscv:

式中:A=1.212;B=0.974+0.175 9◦fv/235;C=0.030 9-0.103 8◦fck/20;fv为钢材屈服点;fck为混凝土轴心抗压强度标准值;ξ为套箍系数。轴压组合比例极限fscp和比例应变εscp分别为:

本文钢管混凝土的屈服强度fscv为63.04MPa,fscp为48.53MPa,抗压弹性模量Esc为:

在弹塑性阶段,假定切线模量Esct按二次抛物线变化,且有:

钢材应力-应变曲线采用理想弹塑性模型,钢材的屈服应力和屈服应变分别为σv和εv。

图2 钢管混凝土的本构关系

2.3 整体缺陷的分布

拱桥的整体几何缺陷在拱跨范围内均有分布,它既可以采用一致缺陷进行描述,也可以采用随机缺陷进行描述。前者通过某种事先假定的几何外形来模拟结构的初始缺陷,后者则基于随机理论得到结构的随机几何缺陷分布方式。

已有文献[3,4]大多采用屈曲模态模拟缺陷的一致描述方法来考虑大跨拱桥中几何缺陷的分布,这种方法将大跨拱桥特征屈曲分析得到的屈曲模态作为几何缺陷模式,施加到结构上用以模拟缺陷。这是由于特征矢量屈曲形状是最接近于实际屈曲模态的预测值,而且特征屈曲荷载作为非线性屈曲荷载的上限,可作为施加初始缺陷或扰动载荷的根据。同时由于屈曲模式是结构潜在的位移趋势,如果拱桥结构的初始缺陷分布恰好与其屈曲模态吻合,将对结构的稳定性产生最不利的影响。

大跨度拱桥的拱肋在各个环节中由于各种原因产生的初始挠度具有很大的随机性,基于随机理论考虑这些几何缺陷影响的方法中,可以将实测得到的初挠度分布进行调和分析,然后计算极值点屈曲荷载;或者将随机理论的方法用于分析任意分布的初挠度对屈曲的影响,建立屈曲荷载与随机初挠度谱密度间的关系。但前者只能针对已建成的拱桥且实测工作量很大,后者公式推导繁杂,最后得到的也不是最不利的失稳形式。本文通过一种新的随机方法分析拱的初始几何偏差,此方法将几何缺陷导致的节点坐标偏差视为随机变量,通过节点之间一定的相关性确定结构的条件相关矩阵,并分解得到按可能性大小排列的随机缺陷分布方式。拱结构中随机分布的节点坐标偏差用平均值、方差以及一定程度的相关性描述,为分析方便坐标偏差假定为正态分布且有相同的数学期望和方差,节点之间的联系以含相关长度参数γ的指数相关函数考虑。令u=[z1,z2,Λ,zn]T为n维随机变量来模拟结构的节点坐标偏离向量,设0和1为拱的边界条件,z和z′表示拱结构(0,1)中的两个随机点,随机变量均为正态分布且方差均为σ2,z和z′之间的协方差可表示为:

其中ρ(z,z′)为z和z′的相关系数,假定z和z′为指数相关,且其相关系数函数为:

式中γ为相关长度参数,支撑边界确定的拱结构中,z和z′的条件协方差可写为:

由上述条件得到的条件相关矩阵Czz可以表示为:

其中,特征向量Ψ即为几何缺陷的分布方式,在实际分析时只选取前几阶影响较大的缺陷。图3给出了图1-a所示系杆拱桥通过条件相关矩阵分解得到的前三阶随机几何缺陷中拱肋轴线在平面内的偏差示意图。

图3 随机整体缺陷下拱肋轴线偏差示意图

本文分析大跨度拱桥在考虑几何缺陷的稳定性时,采用一致和随机两种方法模拟几何缺陷的整体分布,分布方式包括特征矢量屈曲形状和按随机理论得到的前三阶随机分布方式。将这两种描述所得结论进行对比分析,并与无缺陷拱的结果进行比较,确定缺陷的最不利方式以及对结构稳定性能造成非常不利影响的幅值大小。

2.4 局部缺陷的分布

大跨度拱桥的拱肋存在局部几何缺陷时,必将对吊杆间拱肋的局部稳定产生影响。目前研究局部缺陷较多的是柱[10]和板[11]结构,现行的规范均对这些构件的整体及局部初始挠度作了限制以避免出现缺陷降低构件的承载能力。而拱肋存在局部缺陷时结构稳定性的研究现在鲜有文章涉及,拱肋初始局部挠度的大小和位置与承载能力之间的具体关系尚不清楚。针对这一问题本文假定拱肋存在一定的局部缺陷,研究它对拱桥结构稳定性能的影响,这种初始挠度假定沿拱肋呈正弦形式分布,如图1所示,考察它在拱肋不同位置和大小时拱桥的屈曲特性和承载能力。

3 计算分析

3.1 整体缺陷的影响

拱结构整体几何缺陷的分布包括特征屈曲形状缺陷和前三阶随机分布缺陷,这些初始几何缺陷的有限元考虑方法是对完善拱结构进行坐标重新修正。将每种缺陷的幅值取相同值用以比较分布方式对拱桥结构稳定性的影响;另外对于某种确定的缺陷不断变化其缺陷幅值观察它对结构稳定性的影响,并判定使得结构失稳的缺陷幅值。

表1给出了缺陷幅值取为L/1 000情况下,即取缺陷幅值为12.5 cm时,拱桥结构含有这4种缺陷时的稳定系数计算结果。从中可以看出在各种不同分布方式几何缺陷下,弹性大变形即仅考虑几何非线性的稳定系数与线弹性情形相差不大,而同时考虑几何、材料非线性的弹塑性大变形稳定系数则明显下降,这说明了在拱桥的稳定性计算过程中材料非线性是主要的因素,它使结构的承载能力明显下降。另一方面,虽然各种缺陷的幅值均取为L/1 000,但是不同的分布方式对稳定系数影响不同,其中特征屈曲形状缺陷和二阶随机缺陷对拱结构的稳定性影响最为不利,在弹塑性大变形分析中,二阶随机缺陷可使得稳定系数相对无缺陷情形下降15.5%。为了比较这4种缺陷在其幅值发生变化时拱桥的稳定性能,图4给出了缺陷幅值在变大的情况下拱桥弹性大位移稳定系数的分布规律,从中可以看出缺陷幅值达到一定的程度时,安全系数下降明显,其中尤以特征屈曲形状缺陷和二阶随机缺陷影响最大,当幅值为L/500时这两种缺陷使得安全系数下降了近50%,而一阶随机缺陷和三阶随机缺陷对稳定系数的影响则比这两种缺陷小得多。特征屈曲形状和二阶随机缺陷外形比较相似,与结构的潜在位移趋势接近,因而对结构稳定性能影响非常不利,计算结果也很好地说明了这一点。特征屈曲形状缺陷是按照屈曲模态与结构位移趋势相似得到的,而二阶随机缺陷则是基于随机理论得到的,与它们类似的整体几何缺陷外形是拱结构的最不利缺陷分布方式。

表1 不同缺陷大跨拱桥稳定系数

从图4还可知各种缺陷在其幅值处于一定的范围之内时安全系数与无缺陷拱相比变化均较小,而当缺陷幅值进一步增大时缺陷的影响明显加大。计算结果表明各种缺陷在其幅值小于L/1 000时可以不考虑它对稳定性能的影响。为了说明缺陷增大时拱桥考虑缺陷影响的稳定性,图5给出了二阶随机缺陷在不同幅值下拱顶的弹性大位移荷载-位移曲线,从中可看出缺陷增大时承载能力有一定的下降,缺陷幅值越大下降越明显,因而将缺陷大小控制一定的范围内对于保证稳定性极为必要,计算显示缺陷幅值小于L/1 000时含缺陷拱桥的承载能力与无缺陷拱差别不大。

3.2 局部缺陷的影响

对于在拱肋上正弦形式分布的局部几何缺陷,为研究它对局部失稳特性的影响,图6给出了局部缺陷分布在不同的位置时拱桥的弹性大位移稳定系数,其中缺陷幅值为吊杆间距的1/1 000,吊杆间的局部缺陷考虑分布于拱肋上和拱肋下两种情形,其计算结果与无缺陷时稳定系数进行了对比。计算结果显示局部缺陷的位置对稳定性有一定程度的影响:较为敏感的位置位于拱脚和跨中,当局部缺陷分布在这些位置时考虑缺陷的稳定系数与无缺陷情形的差别较大;而当局部缺陷位于拱跨径的1/4附近时缺陷的影响很小。另外由图6还可看出局部缺陷在拱肋同一位置而分别位于拱肋上方和下方时,局部缺陷的影响程度基本相同,但是它们使得稳定系数变化趋势恰好相反。不过从整体上来说,不论局部缺陷的位置如何,稳定系数相对无缺陷情形变化程度还是相当小的,缺陷的影响均在1%内。

图4 不同缺陷幅值下的非线性稳定系数

图5 二阶随机缺陷下的拱肋荷载-位移曲线

为分析局部缺陷大小对稳定性能的影响,图7给出了局部缺陷取不同幅值时拱肋的弹性大位移荷载-位移曲线,其中局部缺陷的分布位置取为图1-c中编号为1位置的拱肋下方和编号为7位置的拱肋上方。图7的计算结果表明不同缺陷幅值下拱顶的荷载-位移曲线几乎完全重合,局部缺陷的大小基本上不对拱桥的承载能力产生影响,因此可得出在计算大跨拱桥的稳定性和承载能力时可以不用考虑拱肋局部缺陷影响的结论。

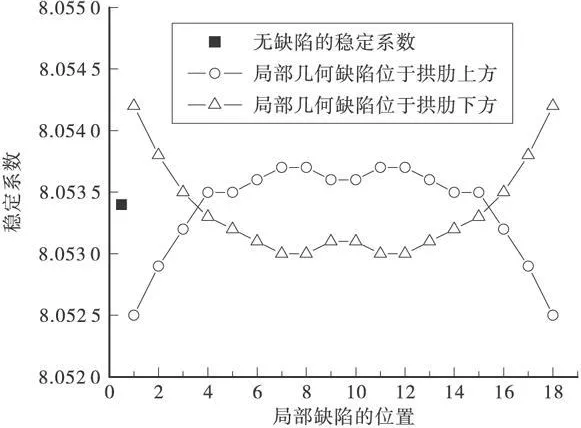
图6 不同局部缺陷位置的非线性稳定系数

图7 局部缺陷幅值变化时拱肋荷载-位移曲线

3.3 拱桥的失稳特性

在分析大跨拱桥的稳定性时,结构的非线性是必需考虑的因素。为此图8给出了拱顶的荷载-位移曲线分别按照线弹性、弹性大位移和弹塑性大位移3种情况的计算结果,其中整体几何缺陷按照随机分布方式2施加,缺陷幅值为L/1 000,局部缺陷不予考虑。计算结果显示在3种分析方法中,线弹性分析方法所得极限荷载最大,仅考虑几何非线性的弹性大位移分析方法次之,同时考虑几何、材料非线性影响的弹塑性大位移分析方法最小,所以在实际大跨拱桥中线性方法和仅考虑结构几何非线性的方法均过高估计结构的承载能力,稳定性计算偏于不安全,在计算拱桥的极限承载能力时必须考虑材料非线性。

图8 特征屈曲缺陷下拱肋荷载-位移曲线

图9则给出了在弹塑性大位移分析过程中,塑性区域的出现顺序及分布位置。荷载从0增加到43.5 kPa的过程,即图9所示的加载阶段1,整个结构处于弹性阶段,拱肋没有塑性区域的分布;荷载从43.5 kPa变大至62.1 kPa时,这一阶段结构的静力非线性分析应考虑几何非线性;当荷载超过62.1 kPa时,左端拱脚上缘拱肋进入弹塑性状态,对应图9所示加载阶段2;而当荷载增至83.2 kPa时,左端拱脚处拱肋的上缘已进入塑性屈服状态,下缘则进入了弹塑性状态,同时1/4处拱肋上缘也开始出现塑性区域分布,如图9所示加载阶段3;当施加荷载达到95.7 kPa后,拱脚处上、下缘的塑性区已经贯通,形成一个塑性铰,拱肋1/4处的塑性区扩大;当荷载进一步增大时,拱肋的塑性区域继续增加,结构位移迅速增大,直至结构发生失稳破坏。

图9 极限加载过程的拱肋塑性区域位置

4 结论

本文在进行大跨度拱桥稳定性分析时,考虑了几何缺陷、几何非线性和材料非线性等因素的影响,几何缺陷的分布从整体和局部上分别考虑,整体缺陷包括由随机和一致两种分布方式,局部缺陷通过吊杆间拱肋的局部初挠度考虑,得出了以下结论:

1)沿拱肋分布的各种整体几何缺陷,当其幅值小于跨径的1/1 000时,可以不用考虑整体缺陷的影响。特征矢量屈曲形状和二阶随机分布方式的缺陷对结构的稳定性能影响最大,在其幅值达到一定程度时结构承载能力有明显的下降,它们是稳定性分析必须考虑的影响因素。

2)对于局部缺陷,通过计算发现存在缺陷时拱桥的稳定系数虽然和无缺陷拱桥存在差异,但是缺陷的影响很小,局部缺陷位于拱肋不同位置时非线性稳定系数相差不到1%,而且局部缺陷的幅值增大时,缺陷对拱肋的荷载-位移曲线的影响基本上可以忽略。

3)通过计算发现线弹性和仅考虑几何非线性的分析方法会过高估计结构的承载能力,大跨拱桥的稳定性分析必须考虑材料的非线性因素。考虑材料非线性的弹塑性大位移分析时,拱肋的塑性区首先出现在拱脚位置上缘,达到极限荷载时分布区域包括整个拱脚与1/4拱肋的上缘。

[1]李国豪.桥梁结构的稳定与振动[M].北京:中国铁道出版社,1996.

[2]程 进,江见鲸,肖汝诚,等.大跨度钢拱桥结构极限承载力分析[J].工程力学,2003,20(2):7-10.

[3]谢 旭,李 辉,黄剑源.大跨度两铰钢拱桥面内稳定分析[J].土木工程学报,2004,37(8):43-49.

[4]徐文平,装铭海,戴 捷,等.大跨简支系杆拱桥非线性稳定性[J].交通运输工程学报,2005,5(4):53-57.

[5]Palamas.J,Coussy.O,Bamberger.Y.Effects of surface irregularitiesupon the dynamic response of bridges under suspended moving loads[J].Journal of Sound and Vibration,1985,99(2):235-245.

[6]Most.T,Bucher.C,Schorling.Y.Dynamic stability analysis of non-linear structures with geometrical imperfections under random loading[J].Journal of Sound and Vibration,2004,276(1-2):381-400.

[7]Schorling.Y,Bucher.C.Dynamic stability analysis for structures with geometrical imperfections[J].In:Structural Safetyand Reliability,Rotterdam,1998:771-777.

[8]王勖成,邵 敏.有限单元法基本原理和数值分析[M].北京:清华大学出版社,1996.

[9]韩林海.钢管混凝土结构[M].北京:科学出版社,2000.

[10]沈祖炎,张其林.受压方管钢柱的屈曲后极限承载力[J].土木工程学报,1991,24(3):15-26.

[11]陈国栋,郭彦林.非加劲板抗剪极限承载力[J].工程力学,2003,20(2):49-54.