三维岩体裂隙网络模拟研究及应用

陈志杰,冯 曦,李傲松

(四川大唐国际甘孜水电开发有限公司,四川康定 626001)

三维岩体裂隙网络模拟研究及应用

陈志杰,冯 曦,李傲松

(四川大唐国际甘孜水电开发有限公司,四川康定 626001)

为合理评价某水库库岸岩体结构特征及工程整治提供依据，对区内岩体进行了裂隙调查及三维网络模拟研究。研究基于Monte-Carlo模拟方法，由走向玫瑰图、倾向和倾角分布的直方图对裂隙的产状分布特征分别进行了分析，结合裂隙等密度图分析得出了结构面优势产状、用直接法产生随机数并利用计算机模拟得出符合实际的三维裂隙网络图。引入广义计算，讨论了值的变化可能影响库岸岩体在不同方向的稳定性。

岩体裂隙；三维网络；模拟研究

1 基本原理

从20世纪80年代初开始研究裂隙网络模拟技术[1]以来，裂隙网络模拟技术已逐渐成熟，其成果已在工程上得到了广泛的应用[2，5]。裂隙网络模拟研究过程一般包括：1）在野外采样的基础上对裂隙样本进行统计分析，包括对样本进行分组和各组样本随机变量（如走向、倾向、倾角、间距、迹长等）的统计；2）对样本分布形式进行拟合优度检验，判断各随机变量的统计分布形式和分布参数；3）根据裂隙各随机变量的统计分布形式，生成符合裂隙分布规律的随机数，并以此生成裂隙网络图。

2 裂隙网络统计与模拟

2.1 工程背景

某库段位于兴山县中部偏南的香溪河谷，为兴山县原县城所在地。区域上位于大巴山与秭归盆地过渡地带，属于构造剥蚀中低山区，山高坡陡，相对高差800～1 000 m。研究区内地层出露齐全，从古元界至新生界均有出露，该地区分布地层有三叠系，侏罗系及第四系。区域地质构造上高阳镇处于3个构造单元的交接部位，区内地质构造复杂，次级褶皱断层发育。

按该水库设计水位，该地区将大部分被淹没，将极大地改变该地区的工程地质条件，进一步恶化其环境地质条件。为研究该库段岩体地质结构特征，进一步为地质灾害防治工程设计施工提供依据，进行此库段岩体裂隙网络模拟研究。

2.2 裂隙野外采样

要进行岩体裂隙网络的计算机模拟，首先必须通过采样由统计分析确定岩体中裂隙空间几何参数的分布形式，需要的参数有：裂隙的空间产状（走向、倾向和倾角）、裂隙的间距、裂隙的迹长等；然后根据几何参数的分布形式进行裂隙网络模拟。对裂隙的几何参数进行采样，常见的测量方法有统计窗法和测线测量法，本次研究采用测线测量法。实际测量是选择在研究区塌岸带内出露最为广泛的香溪组、中—下统聂家山组地层内布置了12条测线，共1 235条节理。

2.3 裂隙几何参数分析统计

裂隙统计分析的方法很多，有玫瑰花图法、直方图法、极点图法和等密度图法等。本次研究中，首先由走向玫瑰图、倾向和倾角分布的直方图对裂隙的产状分布特征分别进行了分析，然后结合裂隙等密度图分析得出了结构面优势产状。

1）裂隙走向分布特征。由图1可以看出：NW组较NE组发育，且裂隙在NW象限内的分布是比较均匀的；而对于NE组则普遍出现裂隙发育较分散的现象，NE组内的裂隙主要集中在0°～40°之间。

2）倾向和倾角。由倾向和倾角分布直方图可以看出：倾向大致呈均匀分布，但多在110°～130°之间和190°～240°之间；倾角大多为陡倾，一般在45°～80°之间。

3）裂隙产状分布特征。根据结构面的统计数据，可以作出结构面的等密度图。研究区内普遍发育的结构面有以下 5 组：15°∠80°，120°∠45°，120°∠70°，195°∠80°和 220°∠65°。

4）间距和迹长。根据前人的工作[1]，裂隙的间距一般服从对数正态分布或负指数分布。在本研究区域内，裂隙的间距服从对数正态分布，裂隙的平均间距较小，一般为0.25～0.30 m。裂隙的迹长分布规律均不与四种常见分布（均匀分布、负指数分布、正态分布和对数正态分布）相吻合，且裂隙的平均半迹长在1.3～1.6 m之间，规模相对较小，如表1所示。

表1 裂隙分布规律及模拟结果统计表

2.3 直接法及裂隙网络模拟过程

本次研究的裂隙有相当一部分随机变量并不服从常见的分布形式（见表1），此时如仍采用常规Monte-Carlo法，则无法产生满足精度要求的随机数或无法继续进行裂隙模拟，而直接法则较好地解决了这个问题。

2.3.1 随机数的产生

从数学上来说如只进行裂隙网络模拟直接法可以取代常规法，其省去了对随机变量进行是否服从某些分布形式的检验和生成相应随机数的数学变换过程，方法更明了，且精度更高，其均值和方差更接近样本，x2检验值更小。下面重点介绍生成裂隙随机数的直接法，具体过程为：

将样本分布的区间 [a，b]划分为n个小区间[a，a1]，[a1，a2],…，[an-1，b]，记样本落入第 j个小区间的概率为pj（1≤j≤N）。

在样本分布区间[a，b]内用蒙特—卡洛法抽取出足够多的均匀分布的随机数，设有M个，其中M为足够大的整数。这样就能产生由M个数构成的随机数库。在此基础上，可以从产生的随机数库中抽取所需要的随机数，使得抽取的随机数在[a，b]范围内的任一小区间内出现的概率与样本出现的概率充分接近，具体方法为：

其中rj为在[0，1]服从均匀分布的随机数。

对任一随机数tj（a≤tj≤b），在规定a0=a，an=b时，若：

成立，则将落该小区间[aj-1，aj]内的数目加1，即：

其中，k为抽取的随机数tj落入该区间的次数，nj为第j个小区间内的随机数的个数。这样，在总共所要抽取的 N随机数中，出现在该区间的随机数的概率为：

对给定的充分接近于1.0的正数ε，若：

成立，表明落入该随机区间的随机数已满足要求，不再需要抽取该区间的随机数，若上式不成立，则重复上述过程，直到每一个小区间内的随机数都满足要求为止。可见，无论样本服从的随机分布多么复杂，都可以完成抽取满足要求随机数的过程。

2.3.2 裂隙的三维网络模拟

在三维网络的模型中，不连续面被模拟成圆盘面。这是因为，根据研究表明，不连续面在其走向方向的长度和其倾向方向的长度大致相等，出于数学方面的原因可简化成为圆盘[2]。圆盘由6个几何参数来表达——坐标系为右手坐标系，x为正北方向，y为正东方向，圆盘的圆心坐标，圆盘的直径d,倾向（x轴正向顺时针到圆盘面指向上的法向量在水平面的投影向量的夹角），倾角（节理圆盘的法向与z轴的夹角）。由这 6个参数可以得到下面的两个方程：

式（5）为圆盘所在平面的空间解析几何方程；式（6）为以点（x0，y0，z0）为圆心，以 d 为直径的球体的球面方程，二者相交即为圆盘的圆周。

三维裂隙网络模拟的具体过程如下：

1）确定模拟范围及范围内不连续面的个数。

2）确定每条不连续面的空间位置：假定节理圆盘面服从均匀分布规则，通过蒙特卡罗模拟方法，随机产生不连续面的中心点坐标。

3）用蒙特卡罗法模拟生成不连续面直径并使其服从已知的最佳概率分布。

4）用蒙特卡罗法模拟生成各不连续面产状。

5）把上述各步骤模拟的结果进行组合，从而形成一个完整的模型。

这样，只要通过在生成域内设置检验域，每生成一条裂隙即对检验域进行一次检验，直到得出的检验域内的裂隙平均面密度与实测结果充分接近来保证生成裂隙数目合理，裂隙间距的分布形式和分布参数就可满足要求[5]。

3 有关问题的探讨

3.1 岩体各向异性广义RQDt值计算

RQD指标被应用于各种岩体工程，在当今最流行的RMR岩体工程分类系统和Q分类系统中，RQD都作为最重要的评定参数。根据Deere的定义，RQD为长度大于0.1 m整段岩芯的累计长度与岩芯总长度之比的百分数。人们发现，在钻探中对于所有岩芯长度都小于0.1 m的岩体，该方法不适合评价岩体的性质，同样的，如果所取得的岩芯长度都大于0.1 m，RQD将为100%，这也不符合实际；通常钻孔深度有限，岩体也是各向异性的，通过钻孔法统计的RQD值只能反映局部的岩体情况，有很大的局限性。

要合理全面地利用RQD 评价岩体的质量应考虑岩体中不同方向及在不同界限长度时RQD的变化规律。在裂隙网络模拟中可以通过裂隙的间距计算出RQD值。

对于任一间距阈值，沿某一测线方向大于间距的岩体与总测线长度之比的百分数定义为广义RQD[3]，用 RQDt表示（在本论文里，t分别取 0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8 m）。即：

式中：n代表长度大于t的间距数目，为大于t的间距长度；L为测线的总长度。

因结构面间距具有随机分布特征，所以RQDt也是随机分布的。RQDt的随机分布规律可用间距的概率函数来表达，其数学期望E（RQDt）描述了岩石质量指标。根据Sen[3]建立了不同间距分布的E（RQDt）模型（结构面的间距一般服从负指数分布或对数正态分布）。当间距呈均匀分布时：

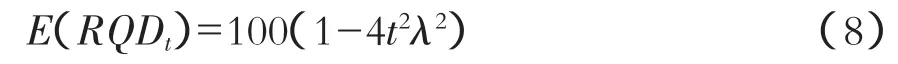
当间距呈负指数分布时：

当间距呈对数正态分布时：

式中：F[x]表示从－∞到x这一区间内标准正态分布曲线下的面积；qnx为间距方差；λ代表结构面的线密度，λ=1/（为结构面平均间距）。

在三维裂隙网络模拟图中，在临空面处进行切割，获得了临空面的迹线模拟图。然后再根据间距分布形式，进行随机抽样产生各种概率分布的随机变量。利用（8）、（9）或（10）式可以较方便地计算出不同方向和界限值所对应的广义RQDt值。

由图2可以看出：在各个阀值所对应的值中,最大的方向是NE24°，最小的方向SE98°，如表2所示。在 NE24°，SE98°方向的RQDt与t所对应的曲线如图3所示。

表2 NE24°方向的RQDt的均值

各块径的RQD在不同方位值变化很大，说明该区结构面的发育情况及岩体的完整性都呈现明显的各向异性，这将必然导致岩体在不同方向上的物理、力学性质差别较大。沿某一方向的RQD值越小，则岩体越破碎；反之，则越完整。在本研究区，岩体为块状结构和层间结合较好的中厚层或厚层状结构，根据GB1350287-99《水利水电工程地质勘查规范》，岩体的RQD大致范围在0.5～0.75，在勘察设计时，NE24°方向阀值 t=0.4 m，SE98°方向阀值t=0.2 m比较合理。在RQD值最小的方向与河谷走向的交角不大，从而使得该区滑坡现象严重[2]。

4 结语

根据以上研究结果及研究区地质调查情况，以下基本结论可供工程应用时参考：

1）研究区内普遍发育的结构面有3～5组，其倾角较陡，一般介于40°～80°之间，倾向以110°～135°，190°～235°，300°～340°方向发育的最为集中。

2）结构面半迹长多在1.0～1.5 m之间，规模相对较小。结构面的平均间距较小，一般为20～49 cm，总体上具有各向异性。

3）该区0.1 m块径时的RQD值很大，一般都达90%左右，而0.3 m块径时为40%～75%，0.5 m块径时为15%～50%左右，0.7 m块径时为6.5%～35%。

4）在通过对岩体出露平面的统计，在各个阀值所对应的RQDt值中,最大的方向是NE24°，最小的方向SE98°。根据规范所提供的岩体质量指标，NE24°方向阀值 t=0.4 m，SE98°方向阀值 t=0.2 m测得的RQDt比较合理。

5）本次研究中采用了直接法和广义RQD值等方法，取得了一定成果，可为评价研究区岩体结构特征和工程整治提供依据，但其研究仍然是初步的，有待进一步深入。

［1］徐钟济.蒙特卡罗方法［M］.上海：上海科学技术出版社，1985：1-144.

［2］孙广忠.岩体结构力学［M］.北京：科学出版社，1988.

［3］杜时贵，何芳象，王思敬.RQD研究的几个理论问题［J］.现代地质，1998（1）.

［4］段蔚平.边坡岩体结构面的模拟［J］.金属矿山，1994（6）.

［5］魏安.岩体裂隙网络的计算机模拟及其应用［J］.西南交通大学学报，1995（4）.

［6］杨天鸿，尚富行.露天矿边坡岩体结构面调查及渗透特性分析［J］.勘察科学技术，1998（3）.

Simulation and application of 3D rock crack network

CHEN Zhi-jie,FENG Xi,LI Ao-song

In order to evaluate the structural characteristics of reservoir bank rock reasonably and supply the basis for project regulation,the rock crack has been investigated in the area and a 3D network simulation is studied.The study analyzes the distribution characteristics of crack occurrence by trend rose and distribution histograms of dip and dip angle based on the Monte-Carlo simulation method and obtained the dominant texture of occurrence by the crack density map,the random number by direct method and the 3D crack network chart by computer simulation conforming to reality.The study introduces the calculation of RQD2 and discusses the possible influence of its value change on reservoir bank rock stability in different directions.

rock crack;3D network;simulation study

X171.3

B

1002－0624（2011）08－0049－04

2011-05-05