振动驱动的电磁－永磁复合驱动建模

吕扬名，杨斌堂，孟光，许文秉，夏明璐，钱文韬

（上海交通大学机械系统与振动国家重点实验室，上海 200240）

工程实际中，动力学环境分析是检验工程实际产品可靠性的关键内容。通过振动台来模拟实际的动力学环境，是当前检测航空、航天器件和精密仪器可靠性的主要技术手段。电动式振动台是由恒定磁场和位于该磁场中的通电线圈相互作用的电动力来驱动,其优点是工作频率范围大，波形失真小，控制方便，可采用反馈控制实现定值振动和随机振动。但是，目前的电动振动台仍存在振幅、激振力不够大，电磁利用效率低、价格贵和结构复杂等问题[1-3]。因此，提出了一种新的振动驱动方式[4]，以求实现电磁－永磁复合磁场激励下的高效振动驱动。针对这种新的驱动方式，进行驱动振动的理论分析和应用实验验证。

永磁体是一个储能器，可以实现机械能、声能和电磁能的转换，可以做成多种功能器件[5]。高磁能积稀土永磁材料作为高效储能元件，其在外部电磁场激励下可能实现电磁－永磁高磁能复合驱动。这种方式具有：直接驱动振动、动态刚性大、驱动响应灵敏、驱动振幅范围宽、结构简单等优点。特别是这种电磁-永磁复合驱动，较一般电动驱动方式潜在具有更高的复合磁场驱动效率。

近年来永磁体越来越多地应用到驱动系统中[6]，有效地描述电磁激励下的永磁部件的动力学特性对实现这类器件的优化设计和控制尤为重要。目前计算电磁力主要基于麦克斯韦应力张量、虚功原理、等效电流和等效磁荷等一般性方法[7-10]，然而对于微小永磁体在电磁激励下产生偏转的电磁-永磁复合电磁扭矩尚未有直接的建模计算方法。文献[11]虽然对电磁扭矩的计算先通过麦克斯韦方程，再借助有限元方法实现了求解，但是这种借助有限元计算的方法却存在计算时间长、网格难以划分和具体表达式不能准确给出等缺点。鉴于此，针对本文永磁-电磁复合驱动研究，作者提出一种基于面磁荷计算电磁扭矩的数值方法。通过这种方法，实现了永磁体转子振动驱动过程的动态建模与模拟，并对这种建模方法进行了实验验证。

1 驱动建模与模拟

1.1 永磁体偏摆驱动

如图1所示，一均匀磁化的椭圆形柱状永磁体转子置于螺线管电磁场中。永磁体转子可在外部电磁扭矩作用下绕轴旋转。

图1 椭圆形永磁体转子置于通电螺线管内Fig.1 Arotary permanent magnet in a solenoid with current

当矢径变化的转子轮廓与输出杆接触时，如图2所示，可实现一种电磁－永磁往复激励下的驱动动作。对于这种永磁体偏摆产生驱动机理，可以用于设计如图2所示的振动驱动机构。该机构主要由永磁体转子、轴、螺线管、输出杆、弹簧和限位卡槽组成。

在初始状态下，永磁体磁化方向保证在水平方向上（图1）。当外部电磁场作用时，永磁体转子在电磁扭矩作用下绕轴旋转；同时，永磁体转子挤压推动输出杆对外做功，从而可推动负载产生驱动。这样，通过对螺线管中施加的电流的强度和频率控制，可以实现对永磁体转子偏摆程度和偏摆动频率的控制，从而可以实现由输出杆带动负载并复合弹簧力作用的往复驱动和振动过程。

图2 振动驱动机构结构简图Fig.2 The schematic of the vibration drive mechanism

1.2 振动电磁扭矩计算建模

对于图2所示振动驱动机构，其关键问题是电磁扭矩的理论建模和计算。针对该问题，本节研究基于面磁荷理论实现了一种计算电磁力作用于永磁体转子转动的扭矩计算和建模方法。

基于等效磁荷模型[12]，永磁体内存在体磁荷，其密度为ρm

式（1）中μ0为真空磁导率，为磁化强度矢量。在均匀磁化的磁体内部，由于∇⋅=0，所以体磁荷密度为零。但是，在磁体边界上由于不连续，仍然存在着面磁荷，其密度记为ρms

其中为面元单位外法线矢量，Br为永磁体剩磁强度，μ0为真空磁导率。

图3 面磁荷示意图Fig.3 The schematic of surface magnetic charge

其中θ为转子偏摆角度（图4），N为螺线管匝数，I为激励电流。

由于外部电磁场加在相邻磁矩的电磁扭矩不能相互抵消[6]，因此，由式（5）将总电磁扭矩假设为

1.3 振动驱动机构力学建模

对图2所示振动驱动机构，假定接触面弹力为理想约束，输出杆被限定在竖直方向上，则可简化为如图4的力学模型。根据哈密顿原理[13]

其中Ek为系统动能，W为主动力所做的功。设某时刻永磁体转子逆时针偏转角度θ，此时m有位移y。

图4 振动驱动机构力学模型Fig.4 Mechanical model of a vibration drive mechanism

其中a，b分别为永磁体转子的长、短半轴；T为外部电磁场对永磁体转子的电磁扭矩；kl为弹簧等效刚度，cl为系统等效阻尼系数，m为位移输出杆等效质量。

式（9）中Iz为永磁体转子对旋转中心（z轴垂直于纸面）的转动惯量。

m在y方向上的速度可记为

于是，δW可改写为联立式（11），（12）可得

式（13）即为振动驱动系统的运动方程。

3 驱动振动模拟和实验验证

表1 系统基本性能参数Table.1 Basic calculation parameters for the system

根据永磁体偏摆驱动原理，我们设计了如图5所示振动驱动机构。为进行该振动驱动机构的振动应用验证，我们进行了实验设置为如图6所示的实验。其中，激光位移传感器用来测量振动驱动机构的输出杆竖直方向上的位移；为防止漏磁，将振动驱动机构置于一铝质台面上。

图5 振动驱动机构Fig.5 Vibration drive mechanism

图6 实验测试过程Fig.6 The experimental process

实验过程中，螺线管电流分别采用了如图7方波和图8三角波激励。对于方波激励，其幅值为5 A，频率为1 Hz；对于三角波激励，幅值为10 A，频率为5Hz。

振动驱动机构在方波激励（如图7）下，有峰值位移0.122 mm。在输出杆峰值位移处，对永磁体转子进行静力平衡分析

其中μ为永磁和位移输出杆之间的静滚动摩擦系数，F为弹簧弹力，T为静平衡状态下电磁扭矩值。

联立式（6），于是可求得，于是可求得c1=6e-5。

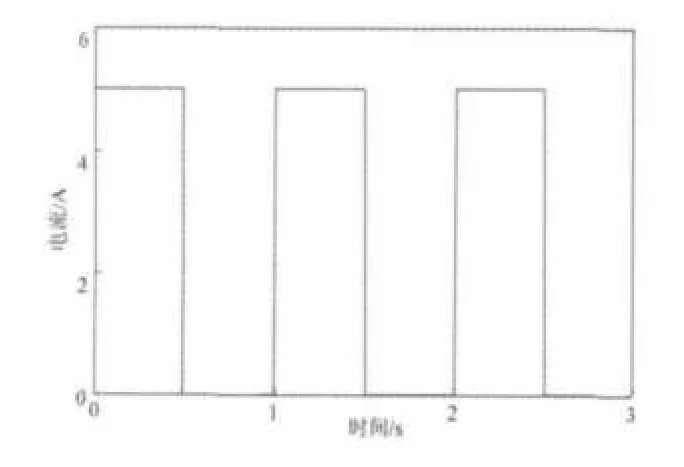
图7 方波激励电流（1 Hz）Fig.7 Square current excitation(1 Hz)

图8 三角波激励电流（5 Hz）Fig.8 Triangular current excitaion(5 Hz)

对图5所示振动驱动机构，由于机构整体设计尺寸的限制，我们未加入竖直方向上（y方向）的限位机构，所以实验过程采用了线性、连续变化的三角波激励。

图9 方波1 Hz实验曲线Fig.9 1 Hz square current experiment curve

图10 三角波实验与模拟对比(5Hz)Fig.10 He comparison between experiment and model

模拟位移和实验测量对比曲线如图10所示，在实验过程中，分别进行了三角波激励下的多周期测试。实验测试表明，该振动驱动机构位移输出稳定、周期性良好。由模拟和实验对比，我们知道，两者周期相同，振动变化趋势一致；但是，由于系统摩擦和弹簧预紧等原因，机械响应延迟，实验测试数据略滞后于模拟结果（实验响应滞后量约0.05 s）。因此，所建立的模型已能够较好地表征所测试的振动驱动机构的输入和输出响应关系，并能较好地模拟机构驱动振动过程。

随着激励频率的增高，永磁体转子和位移输出杆可能出现瞬间脱离，这将影响到整个振动驱动机构工作的稳定性和可控性。因此，在后续的设计研究工作中，应增加弹簧的刚度并调整激励电流的加载波形和强度，以及增加机械限位措施，从而提高整个机构的驱动精度和稳定性。

4 结语

基于面磁荷，提出一种计算电磁扭矩的新方法，通过这种计算方法所得到的计算模拟结果与实验测量结果相吻合，验证了所提出计算方法的正确性和应用的可行性。尤其是对大电流激励的情况，实验和模拟结果一致性良好。该理论模型能在一定电流和偏摆角度范围内为电磁－永磁复合电磁扭矩的预测和模拟提供可靠的参考。对于电磁-永磁复合驱动振动机构，相比方波激励模式，三角波的激励下驱动机构驱动响应和稳定性较好；方波激励由于信号变化不连续，冲击有可能使得输出杆和转子瞬间脱离程度更大，这些都可能使得没有限位机构的振动驱动系统呈现不稳定。本研究所提出和实现的电磁－永磁复合驱动振动计算模拟方法对未来实现电磁－永磁复合驱动振动机构和器件的设计将具有较好的应用价值。

致谢：

本文研究得到上海航天基金、机械系统与振动国家重点实验室重点基金(MSVZD201102)支持，并由国家自然科学天文联合基金（No.10778620）以及973计划（No.2011CB706803）部分支持完成，在此对所给予的大力支持表示诚挚感谢。

[1]杨松,李声远,王晓耕.卫星动力学环境模拟试验技术展望[J].航天器环境工程,2002,19(2)：19-23.

[2]吴三灵,实用振动测试技术[M].兵器工业出版社,1994.

[3]奚德昌,赵钦淼.振动台及振动试验[M].北京：机械工业出版社,1985.

[4]杨斌堂,孟光.永磁伸缩机构[P].中国：200710047397,2007.

[5]周寿增,董清飞.超强永磁体[M].北京：冶金工业出版社,2004.

[6]Štěpánek Jiří,Rostaing Hervé,Delamare Jérôme,et al.Fast dynamic modeling of magnetic micro-actuator[J].Journal of Magnetism and Magnetic Materials,2004,272-276:669-671.

[7]J.L.Coulomb.A methodology for the determination of global electromechanical quantities from a finite element analysis and its application to the evaluation of magnetic forces,torques and stiffness[J].IEEE Trans.Magn.1983,MAG-19,no.6:2514-2519.

[8]J.L.Coulomb,et al.Finite element implementation of virtual work principle for magnetic or electric force and torquecomputation [J].IEEE Trans.Magn.,1984,MAG-20,no.5:1894-1896.

[9]T.Kabashima,A.Kawahara,andT.Goto.Force calculation using magnetizing currents[J].IEEE Trans.Magn.,1988,24,no.1:451-454.

[10]S.H.Lee,I.H.Park,and K.S.Lee.Comparison of mechanicaldeformation duetodifferentforce distributions of two equivalent magnetization models[J].IEEE Trans.Magn.,2000,34,no.4:1368-1372.

[11]Pan Zheng.Forceand torquecharacteristicsfor magnetically driven blood pump[J].Journal of Magnetism and Magnetic Materials,2002,241:292-302.

[12]汤双清,沈洁，等.基于磁荷模型的永磁体空间磁场的有限元分析与计算[J].三峡大学学报(然科学版)2003,25（5）：452-455.

[13]叶敏,肖龙翔.分析力学[M].天津：天津大学出版社,2001.