不确定状态下再制造系统的最优回收批量策略
2011-02-20汤雅青季建华
汤雅青, 季建华
(上海交通大学安泰经济与管理学院, 上海 200052)
0 引 言
再制造(remanufacturing)是指对废旧产品的回收、检测和评估、加工的行为,适用于电子产品、汽车、家电等行业.随着法律制度的完善和人们环保意识的增强,再制造凭借着在环境保护、资源节约等方面的突出作用,越来越受到工业发达国家的重视.另一方面,许多研究表明再制造工程能为企业带来显著的经济利益[1-3].
近年来,国内外许多学者都对再制造做了大量研究.Atasuetal(2008)[4]、Dobos和Flori-ska(2008)[5]等学者研究了再制造的经济效益,Toktayetal(2000)[6]、Gregory(2006)[7]等学者研究了再制造企业的库存管理,Danieletal(2003)[3]、Ismail和Elif(2006)[8]等学者对再制造系统中废旧回收产品的定价以及再制造产品销售的定价策略进行了研究.国内的研究主要集中在制造/再制造混合系统中的最优生产批量控制[9]、库存最优控制[10,11]、再制造系统的回收模式[12]等.
本文在Michael R. Galbreth和Joseph D. Blachburn(2010)[13]的基础上对再制造系统产品回收的最优策略进行了研究.在Michael和Joseph(2010)[13]的模型中,再制造企业回收的产品的质量状态是不确定的,假设回收成本与状态无关,再制造成本是状态变量的线性函数.再制造企业的回收成本会随着回收批量的增加而增加,但再制造成本随回收批量的增加而减少,这是因为回收批量增加后,企业可以仅选择状态好的回收产品进行再制造,因此企业需要在回收成本和再制造成本之间权衡,得到使总成本最小的回收批量.但是此模型只考虑了单个生产周期、确定需求时的情况,回收的产品除去用于再制造外,其余的全部在当期报废,这对生命周期较长的回收产品(如打印机、汽车等)并不适用.对于生命周期较长的回收产品,往往有多个生产周期,不同周期回收的产品的质量状态可能会有较大的差异,再制造成本也会明显不同.因此,本文在Michael和Joseph(2010)[13]模型的基础上研究了多周期的情况,提出回收的废旧产品除了用于再制造外、报废处理外,还可以存储至下一周期再决定去向,综合考虑回收产品的存储成本和不同周期回收的产品的状态差异,以再制造系统总成本最小化为目标,考察了需求确定和需求不确定时的最优回收批量问题.
1 假设与符号说明
1.1 假设
再制造企业从供应商(可以是专门的回收机构,也可以是零售商或用户)手中回收一定批量Q的状态未知的废旧产品,单位回收成本是常数.回收后,通过对产品的检测和评估,确定产品状态和再制造成本,再制造成本是状态变量的函数.回收的废旧产品有以下3种处理方式:(1)用于再制造;(2)直接做废弃处理;(3)记入库存,存储至下一个周期再决定.
本文根据对问题的描述做出如下假设:(1) 认为对回收的废旧产品的检测结果是完全正确的;(2) 对回收批量没有容量限制,但废弃产品的库存有容量限制;(3) 废旧产品的回收成本与状态无关;(4) 再制造成本是回收产品状态的线性函数,即单位再制造成本为c+vm.在一个再制造周期中,我们考虑选择合适的回收批量使该周期的再制造系统总的期望成本最低,总成本包括废旧产品的回收成本、再制造成本、废弃产品的报废成本和库存成本,当需求不确定的时候还有可能存在再制造产品的库存成本和缺货损失.
1.2 符号说明
本文所用到的符号约定如下:D:再制造产品的需求量;m:回收产品的状态变量,g(m)为密度函数;a:收购回收产品的固定成本;u:回收产品的单位收购成本;s:回收产品的单位报废成本;h:回收产品的单位库存成本;c:再制造的固定成本;v:再制造的变动成本;H:再制造产品的单位存储成本;P:再制造产品的单位缺货成本;w:回收产品的产出比率;Q:回收产品的批量,决策变量.
2 需求确定下的最优策略
需求D确定时,再制造企业回收批量为Q,生产批量为D,根据回收产品的3种处理方式,在回收批量Q和上一周期的库存Q-D中选择状态最好的D件回收产品进行再制造,状态最差的Q-D件回收产品做废弃处理,其余的Q-D件回收产品记入库存.所以,再制造系统的总成本为:
f(Q)=a+uQ+(c+vm)D+s(Q-D)++h(Q-D)+
(1)
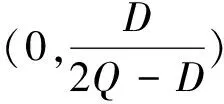
(2)
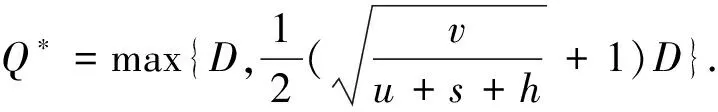
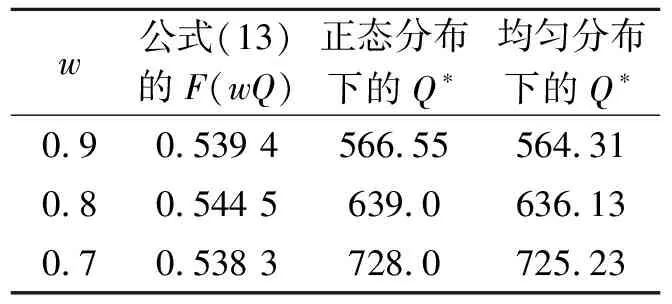
推理1:当v 当回收产品的最佳状态和最差状态的成本差小于单位回收成本、报废成本和库存成本之和时,最佳的回收批量就是需求量. 证明: (3) 对(3)式求Q的一阶导数得 (4) (5) 以上只考虑了统计意义下状态变量服从均匀分布的情况,忽略了每个回收产品状态的不确定性.下面考虑每个回收产品的状态. (7) 性质2:考虑每个回收产品状态的不确定性后,回收产品的状态服从均匀分布且再制造成本是状态分布的线性函数,则在需求D确定时,最优的回收批量Q*为: (8) 证明: 即 (9) 同样地,对f(Q)求一阶导数,可以得到 (10) 需求不确定时,此时的再制造批量无法根据需求确定.企业基于回收批量按一定的比例w进行再制造,即在回收批量Q和上一周期的库存Q-wQ中选择状态最好的wQ件产品进行再制造,状态最差的Q-wQ件回收产品做废弃处理,其余的Q-wQ件回收产品记入库存. 再制造系统的总成本包括回收产品的收购成本和再制造成本、再制造产品的存储成本和缺货成本、废弃产品的报废成本和库存成本,即 f(Q)=a+uQ+(c+vm)wQ+H(wQ-D)++p(D-wQ)++s(Q-wQ)+h(Q-wQ) (11) 性质3:使(11)式的总成本最小的最优回收批量Q*满足如下表达式: (12) 其中F(x)为需求的分布函数. 证明: (13) 对(13)式求Q的一阶导数,得: (14) 参数设置见表1. 表1 数值分析的参数设置 表2 需求确定时不同需求下的最优回收批量及产出率 根据公式(2)和公式(8),得到不同需求下的最优回收批量和相应的产出率,结果见表2. 表3 需求不确定时不同产出率下的最优回收批量 从表2可以看出:考虑每个回收产品状态的不确定性后,产品的产出率随着D的增加而减少,但变化趋势非常缓慢,D较大时产出率恒定. 根据公式(12)得到不同需求分布和不同产出率下的最优回收批量,见表3.正态分布均值为500,标准差为100,均匀分布参数设置为(400,600). 从表3可知:产出率对最优回收批量有显著的影响,回收批量随产出率的增加而减小;需求服从不同的分布函数对回收批量的影响并不明显. 本文基于回收产品状态的不确定性,考虑再制造系统中回收产品的3种处理方式,以再制造系统的期望成本最小为目标,分别研究了需求确定和需求不确定两种情况下最优的回收批量问题.在需求确定时,最优回收批量是需求的近似线性函数;在需求不确定时,不同的需求分布函数对最优回收批量的影响并不大. 参考文献 [1] V. Daniel R. Guide, L. N. Van Wassenhove. Managing product returns for remanufacturing[J].Product and Operations Management,2001,10(2):142-155. [2] Michael R. Galbreth, Joseph D. Blachburn. Optimal acquisition and sorting policy for remanufacturing[J]. Production and Operations Management, 2006,15(3):384-392. [3] V. Daniel R. Guide, R. H. Teunter, L. N. Van Wassenhove. Matching demand and supply to maximize profits from remanufacturing[J].Manufacturing and Service Operations Management, 2003, 36(4):319-331. [4] Atalay Atasu, V. Daniel R. Guide, L. N. Van Wassenhove. Product reuse economics in closed-loop supply chain research[J]. Production and Operations Management, 2008,17(5):483-496. [5] Imre Dobos, Adel Floriska. The efficiency of remanufacturing in a dynamic input-output model[J].Central European Journal of Operations Research, 2008,16(3): 317-328. [6] Toktay, L. B., L. M. Wein, S. A. Zenios. Inventory management of remanufacturable products[J]. Management Science, 2000,46(11):1 412-1 426. [7] Gregory A. Decroix. Optimal policy for a multiechelon inventory system[J]. Operations Research, 2006,54(3):532-543. [8] Ismail Serdar Bakal, Elif Akcali. Effects of random yield in remanufacturing with price-sensitive supply and demand[J]. Production and Operations Management, 2006,15(3):407-420. [9] 代 颖, 马祖军. 制造/再制造混合系统的最优生产批量模型[J]. 西南交通大学学报,2004, 41(1):161-121. [10] 顾巧论, 季建华. 基于市场的再制造/制造系统集成库存随机最优控制研究[J]. 系统工程理论与实践,2006,(1):53-59. [11] 缪 周, 徐克林, 陆 瑶. 考虑不确定回收率的制造/再制造系统的EOQ模型[J]. 工业工程, 2009,12(1):132-135. [12] 孙晓晨, 陈秋双, 李 响, 等. 再制造系统废旧产品回收的最优控制策略[J]. 计算机集成制造系统,2007,13(9):1 820-1 825. [13] Michael R. Galbreth, Joseph D. Blachburn. Optimal acquisition quantities in remanufacturing with condition uncertainty[J]. Production and Operations Management, 2010,19(1):61-69. [14] Mark Ferguson, V. Daniel R. Guide, Eylem Koca, Gilvan C. Souza. The value of quality grading in remanufacturing[J]. Production and Operations Management, 2009,18(3):300-314. [15] Atalay Atasu, Miklos Sarvary, L. N. Van Wassenhove. Remanufacturing as a marketing strategy[J]. Management Science, 2008,54(10): 1 731-1 746. [16] 薛顺利, 徐 渝, 苏 军. 再制造系统最优合同设计[J].中央财经大学学报,2007,(4):71-76.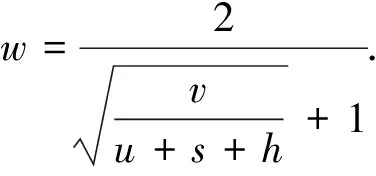
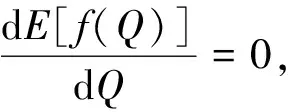
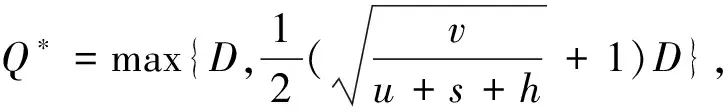
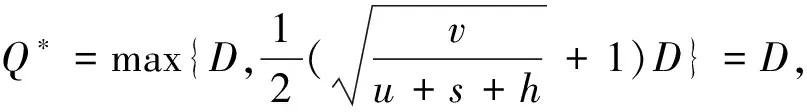
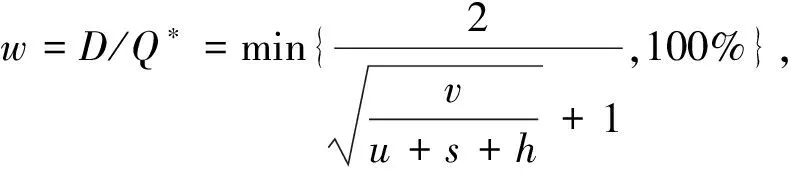
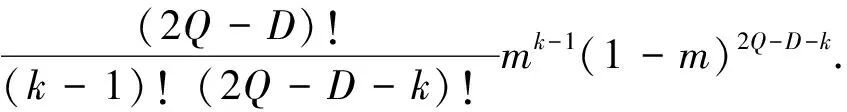
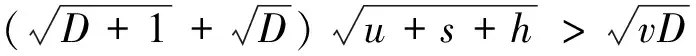
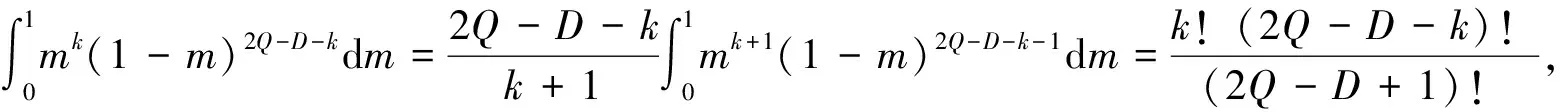
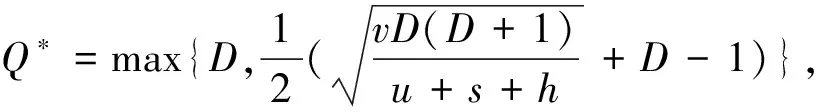
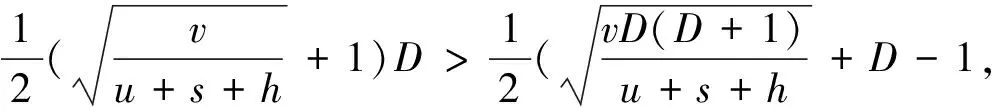
3 需求不确定下最优策略
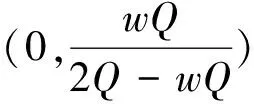
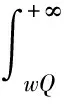
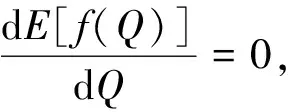
4 数值分析

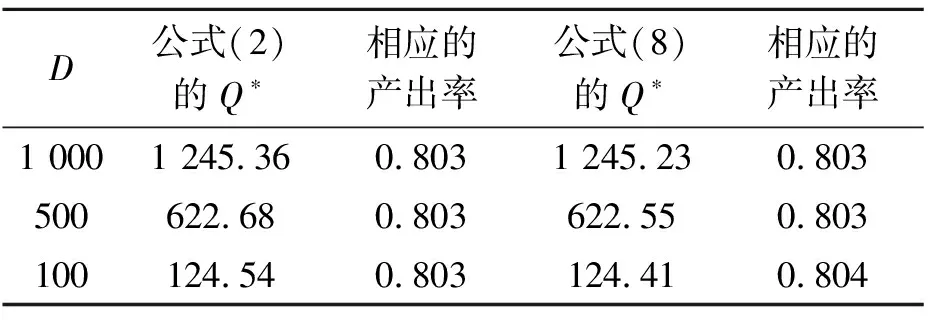
5 结束语
