基于匈牙利算法的自动化立体仓库出入库优化调度

栾 飞， 杨 玮

(陕西科技大学机电工程学院， 陕西 西安 710021)

0 引 言

目前，随着经济危机的加剧，制造企业要生存就必须不断地降低成本，提高企业的适应力和竞争力.立体仓库是企业生产过程中的重要存储设备，提高它的运行效率可以大大减少生产辅助时间，降低存储成本，提高生产效率.要提高立体仓库的整体作业效率，必须对出入库作业进行合理调度，对货位、堆垛机行走路线进行优化，以减少货物搬运次数、货物出入库的等待时间等.

国内外学者在这方面进行了广泛的研究，并取得了一定的进展.山东工业大学的田国会等[1]针对自动化立体仓库的实际运行过程，提出了影响仓库运行效益的若干优化调度问题，并分别采用时态逻辑、模拟退火、遗传算法、神经网络等方法进行了仿真研究；徐香玲[2]、刘韬[3]、王雯等[4]分别用专家系统、赋时Petri网、遗传算法对自动化立体仓库整个出入/库调度过程进行了仿真研究；陈国仁等[5]用聪明蚁群算法来进行堆垛机作业路径调度规划.研究结果都表明这些方法确实可以提高自动化立体仓库的作业效率，但其基本都是属于集中式控制，存在着结构僵化，系统适应性差、容错性差等问题.

本文主要研究基于匈牙利算法的自动化立体仓库的出入库调度优化问题，而采用合理的方法和模型解决其所包含的优化调度问题是整个问题的关键, 可以从根本上提高仓库的运行效率和企业的经济效益.本文主要使用的研究方法有匈牙利算法、AHP层次分析法、Petri网.

1 自动化立体仓库出入库优化的模型建立

1.1 货位指派问题的研究

由于仓库所要存放的货物种类、货物数量出入库频率均有一定的范围,因此我们可以对仓库的库位进行分区规划.在进行货位分区时，可作如下假设：(a)货物的存放种类已知.(b)货物每种类的单位时间内存放的数量己知.(c)每一种货物的存取频率已知.因此建立权值矩阵，单位时间内堆垛机取放某种货物的工作量与该货物的出入库频率和该货物存放的位置有关，将该货物的出入库频率乘以堆垛机运行至存放位置所用时间作为权值因子，即：

Cij=fi×Tj

(1)

其中fi-i种货物的出入库频率,Tj-堆垛机从原点到j区取放的标准时间(Tj=j×T间).

经过以上处理，仓库的初始分区及第一次开始存放变为一个区内放入一种货物，某一种货物放入某一区后即不能再放入其他区，某一区放入某一货物后也不能再放其他货物.这变成为指派问题.可以建立如下的数学模型：

(2)

1.2 立体仓库巷道指派问题的研究

自动化立体仓库的系统评价也是属于多目标、多判据的系统评价.对于多巷道立体仓库来说，各个巷道库存状况和堆垛机的状态都是不同的.所以对于完成某个入/出库任务来说，就存在一个较为优选的巷道来完成任务更为合适.不同巷道指标不同，不同的指标具有的重要程度也不同.

在确立了评价指标的基础上，结合立体仓库的实际情况，利用层次分析法[6]建立层次分别针对入库和出库任务给出的各项标准的重要性进行两两比较.最终确定了出入库的权重,最终结果见表1、表2.

表1 入库指标及权重

表2出库指标及权重

备选方案权重巷道堆垛机累计工作时间0.229 5出库货物在该巷道的现存数量0.121 0该巷道接收任务预计完成时间0.329 0该巷道中该种类货物的入库时间0.166 7该巷道待出入库任务数量0.153 8

1.3 巷道的出入库能力计算

本课题研究所建立的模型为三巷道的立体化仓库，因此以三巷道完成3项任务为例来研究匈牙利算法应用于立体仓库调度多任务分派问题时，效益矩阵代表的意义以及效益矩阵各项代表的意义.a11a21a31代表1巷道完成3项任务分别需要付出的代价，a12a22a32代表2巷道完成3项任务分别需要付出的代价，a13a23a33代表3巷道完成3项任务分别需要付出的代价.即三巷道完成3项任务时，需要计算9个数值:

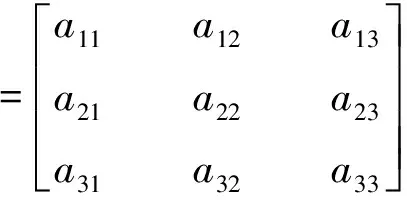
(3)

阵中各项的计算方法相同，下面以a11为例介绍各项的计算方法，以多任务入库为例，各巷道入库能力评价指标及权重见表1所示，各个指标的获取方法在根据实际假设出来后，再结合各指标对应的权重进行计算，计算方法如下：

a11=α×x1+β×x2+γ×x3+δ×x4+ε×x5

(4)

a11:实体巷道1接受任务的代价;α，β，γ，δ：衡量巷道能力的指标权重；x1,…,x5：入库能力衡量指标计算值,其他各项与a11的计算方法相同,最后可得到效益矩阵.

2 基于匈牙利算法的自动化立体仓库出入库的调度优化

2.1 匈牙利算法[7]的原理

一个关于矩阵中0元素的定理：系数矩阵中独立0元素的最多个数等于能覆盖所有0元素的最少直线数,这种解法称为匈牙利法.有n个实体巷道，怎样指派n种货物去选择巷道；有n项货位，怎样指定n种货物去放货取货,这就需要利用匈牙利算法去解决最优指派问题.由于每个巷道出入库能力不同，各巷道完成的任务不同(或所费时间)，效率也不同,于是产生了应指派哪个巷道去接受哪项任务的问题，以便使完成n项货物的总效率最高(或所需的总时间最小).如何有效地指派货物选择的巷道，并进行合理有效的货位选择，就成为自动化立体仓库需要解决的重要问题.

此模型也说明了第j项货物只能由1个巷道去完成；第i个巷道只能接收1种货物.解矩阵Xij中各行各列的元素之和都是1.匈牙利算法的一般流程如图3所示.

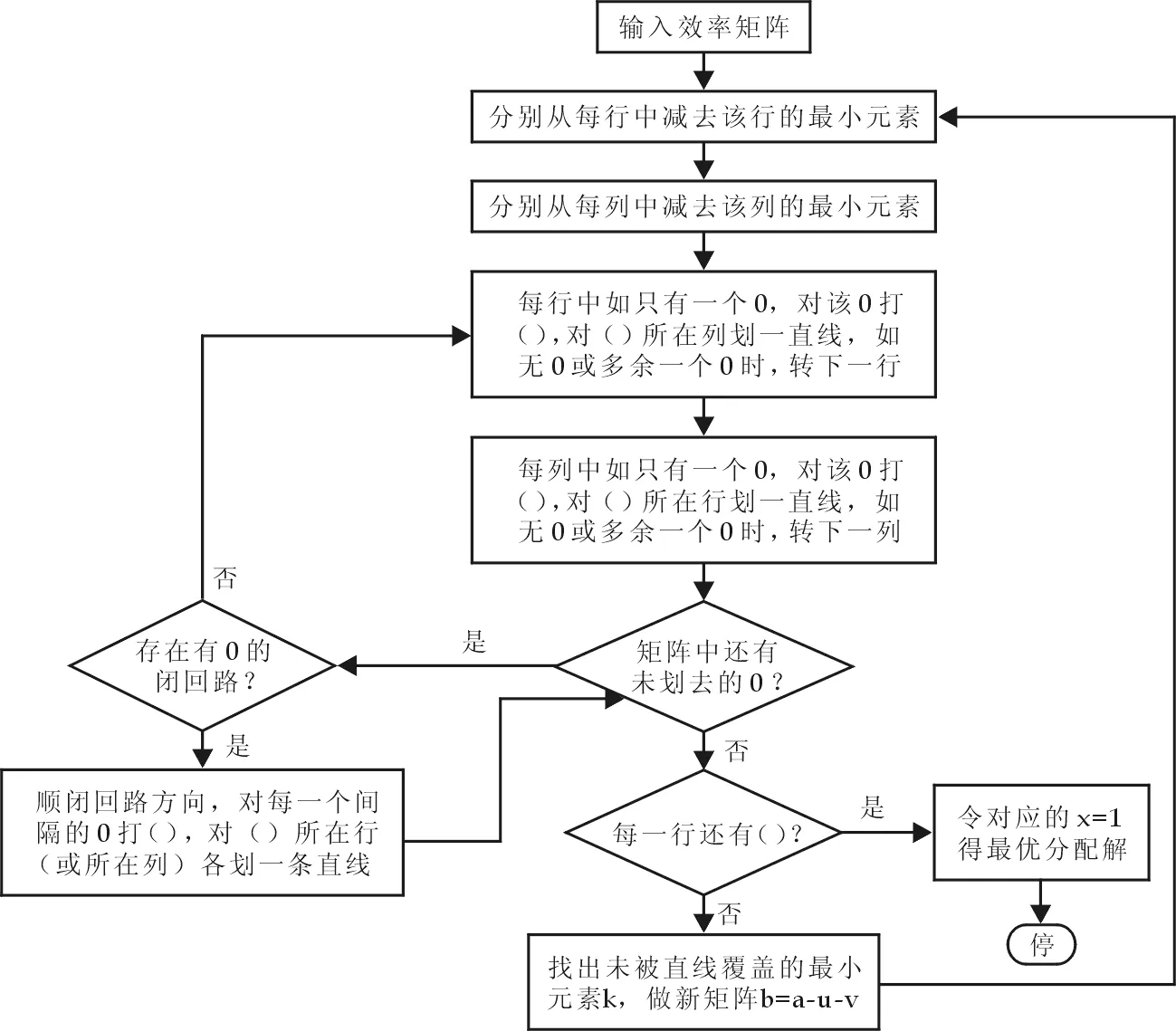
图3 匈牙利算法的计算流程图

2.2 货位优化实例

由于多任务入库过程与多任务出库过程相似，因此我们只讨论多任务入库过程.在已知各个出库指标数据的情况下，可以得出各个巷道接收每种货物的入库代价,见表3.利用匈牙利算法优化效益矩阵可以得出最终优化结果,见表4.因此，利用匈牙利算法优化后可以得出货物1→2巷道，货物2→3巷道，货物3→1巷道.

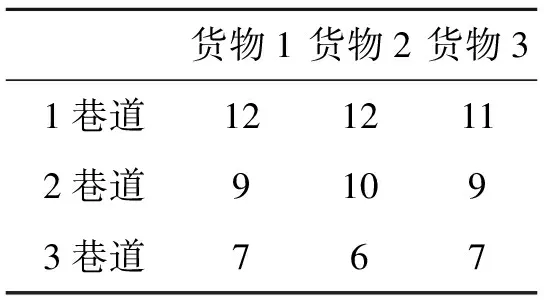
表3 各巷道接收货物所需代价表

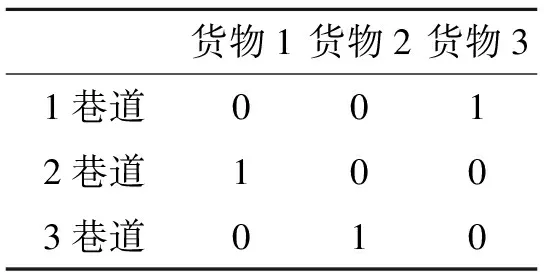
表4 最优指派方案

2.3 巷道优化实例

由于本课题研究的需要，我们在此只考虑一次指派问题，并把所解决的问题简单化了.在立体仓库模型已经建立的基础上，我们把4层5列(一共300个货位)的仓库分为5个区域：A、B、C、D和E区.根据本课题所建立的自动化立体仓库以及假设的参数，可以得出堆垛机的运行时间，在其条件下可以计算出权值矩阵，并将其权值矩阵经行优化，得出合理的指派.因此，可以得出权值矩阵Cij,见表5.经过一系列的匈牙利算法得到最优指派方案,见表6.零件1→B区，零件2→D区，零件3→E区，零件4→C区，零件5→A区.

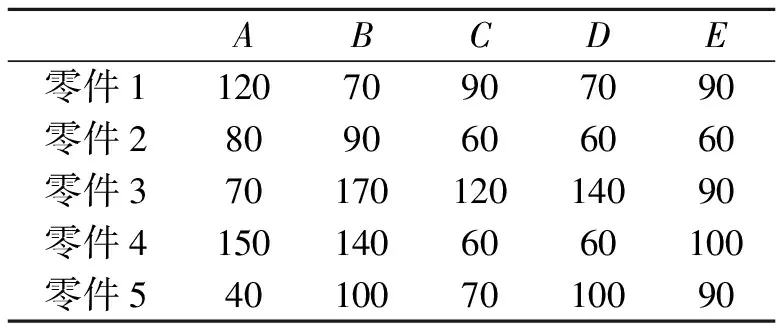
表5 权值矩阵

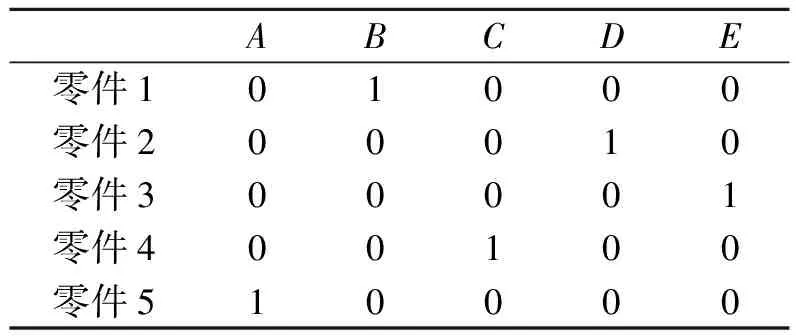
表6 最优指派方案

3 立体仓库出入库调度Petri网的模拟仿真

自动化立体仓库的出入库执行过程是一个离散的事件序列.在各种方法中，Petri网可以很好地模拟这样的离散事件系统,可分为6个对象模块：入库缓冲区模块、入库台模块、堆垛机入库模块、堆垛机出库模块、出库台模块和出库缓冲区模块.各个模块间相互独立，通过过渡变迁联系起来.因此采用Petri网仿真建模软件VisObjNet来建立系统的自动化立体仓库仿真模型，并对其进行仿真，结果显示其效果良好.

4 结束语

本文利用指派问题对货位划分区域进行货物的指派，并结合了匈牙利算法优化，较好地解决了货位指派、巷道选择的合理化问题.建立了出入库调度问题的数学模型，并根据调度原则提出了约束条件.最后研究了运用Petri网来模拟仿真自动化立体仓库出入库调度过程.考虑到仓库管理的复杂性和特殊性，纯粹地数学分析难免以偏概全而导致实用性的丧失，本文在建立模型假设研究的基础上，采用的匈牙利算法并对立体仓库调度优化进行了改进.

参考文献

[1] 田国会.自动化立体仓库若干优化调度问题及其研究进展[J]. 山东工业大学学报，2001,(2)：12-17.

[2] 徐香玲，傅卫平，李德信,等.基于专家系统的自动化立体仓库出入库调度研究[J]. 物流技术，2005，(2)：38-40，51.

[3] 刘 韬，傅卫平，王 雯,等.基于面向对象赋时Petri网的出入库系统建模[J]. 系统仿真学报，2006，18(3)：537-541.

[4] Wang W, Fu W P, Ma M Y,etal.. Selection of AS/RS scheduling rules based on genetic algorithm[C]. Proceedings of the IEEE International Conference on Automation and Logistics, ICAL 2007:536-540．

[5] 陈国仁. 物流输送系统的智能控制与调度研究[D]. 北京：北京机械工业自动化研究所硕士学位论文，2004.

[6] 庄锁法. 基于层次分析法的综合评价模型[J]. 合肥工业大学学报(自然科学版)，2000,23(4)：582-590.

[7] 张旭辉，朱宏辉，郑启忠. 最优指派问题匈牙利算法的探讨与C++实现[J]. 物流技术，2004:(5)：67-69.