RSS′R机构的主从动件等速度点及速比的简便求法

王允地， 杨新宇， 王良文， 张航伟

(1.陕西科技大学机电工程学院, 陕西 西安 710021；2.郑州轻工业学院机电工程学院, 河南 郑州 450002)

0 引 言

主从动面垂直的RSS′R机构在工业缝纫机、纺织机械等行业中获得了广泛应用.虽然众多学者对其运动分析的解析法及位移分析的图解法进行了讨论，但还没有探讨对其进行速度分析的图解法[1-9].王允地等在文献[1]中研究了此种RSS′R机构主从动件运动参数及连杆空间运动参数的解析分析法.祝毓琥等在文献[2]中介绍了此种RSS′R机构从动件角位移的图解法.

本文根据空间运动刚体的速度投影定理[10]及主从动面垂直的RSS′R机构的内在联系，找到了主从动件上的等速度点，据此给出了主从动件速比的简便图解法.文中还对从动件角位移及机构压力角的图解法进行了补充讨论,并对两种常见的空间曲柄摇杆机构的极位条件进行了研究.利用本文所述的理论和方法，可以方便地设计出满足给定摆角及结构要求的空间曲柄摇杆机构.

1 主从动面垂直的RSS′R机构的示意图

主从动面垂直的RSS′R机构的示意图如图1.空间直角坐标系Oxyz的zox面是主动件AB的回转平面，yoz面是从动件DC的回转平面.主动件AB的长度为a,从动件DC的长度为c. 空间连杆BC的长度为b,球面副B的回转中心A位于Ox轴上，坐标为X；球销副C的回转中心D位于yoz面上，其坐标分别为Y及Z.主动件AB相对于z轴方向转角为φ1，从动件DC相对于y轴方向转角为φ3.

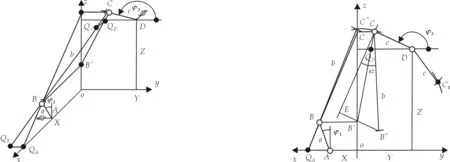
图1 RSS′R机构的示意图 图2 角位移、压力角及速比的图解法

2 从动件角位移及机构压力角的图解法

过球销副中心C作DC的垂线，并从B′向其作垂线，垂足为E点.以C为圆心，以连杆长b为半径画弧，与直线EB′交点为B″，则EC与BC的夹角α便是机构在此位置的压力角.

3 主从动件上的等速度点及速比

参看图1，记连杆BC与xoy面的交点为QB，与过从动件回转中心D且与xoy平行的平面的交点为QC，QA为QB在主动面zox上的投影，QD为QC在从动面yoz上的投影.由空间运动刚体的速度投影定理可知，主动件上QB点及从动件上QC点两者的速度在BC连线方向的投影相等，又因QB与QC两者的速度方向相同(均平行于Z轴)，因此，两者速度必然相等.

QB与QC处在主动件回转轴的同一圆柱母线上，QD与QC处在从动件回转轴的同一圆柱母线上，因此，主动件上的QA点与QB点速度相同，从动件上的QD点与QC点速度相同，综合得知，主动件上的QA点与从动件上的QD点速度相等.

参看图2，连B′与C点，与过D且与Z轴垂直的直线相交，其交点即为QD点.从球销副C向Z轴作垂线，垂足为C′，连C′与B点，与X轴的交点即为QA点.

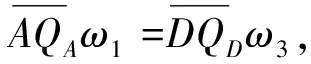
从公式看出，连杆BC在主动面投影与主动件AB共线，通过主动件回转中心A时，A与QA重合，从动件角速度为零.

4 两种常用的空间曲柄摇杆机构的极位条件

4.1 主动件回转中心位于主、从动面交线上的空间曲柄摇杆机构

参看图3，对于偏距X等于零，即主动件回转中心A位于Z轴的情况，当曲柄转到在上部与Z轴重合及在下部与Z轴重合时，主动件上的等速度点QA均与A点重合，摇杆DC的角速度为零，分别处于远极位DC1和近极位DC2.另外，当曲柄AB在两个区间内运动时，摇杆的运动规律对称.图3中取Y=40 mm,Z=70 mm,a=10 mm,b=70 mm,c=30 mm.

此类空间曲柄摇杆机构在工业缝纫机切刀部分及弯针部分的大量使用，使得整机结构更加紧凑.

4.2 从动杆动铰极位处于主、从动面交线上的空间曲柄摇杆机构

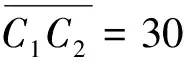
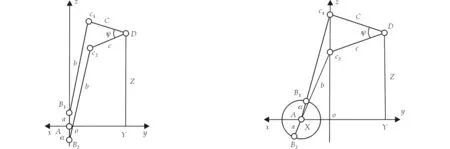
图3 曲柄中心位于Z轴的RSS′R机构 图4 摇杆动铰极位处于Z轴上的RSS′R机构

5 结 论

(1)分析出SRR′S机构的位置，做出连杆在主动面上的投影线与过主动件回转中心且与主、从动面交线垂直的直线的交点，得到主动件上的等速度点.再作出连杆在从动面上的投影线与过从动件回转中心且与主、从动面交线垂直的直线的交点，得到从动件上的等速度点.主动件回转中心到其上等速度点的距离与从动件回转中心到其上等速度点的距离的比值即为从动件角速度与主动件角速度的比值.

(2)主动件回转中心处于主、从动面交线上的空间曲柄摇杆机构的极位条件是曲柄转到与主、从面交线重合的位置.而从动件动铰极位处于主、从动面交线上的空间曲柄摇杆机构的极位条件则是曲柄和连杆在主动面内处于拉直及重叠共线位.

(3)本文的理论和方法可以推广到主、从动面不垂直的一般SRR′S机构中去.

参考文献

[1] 王允地.机构连杆空间运动分析[J].西北轻工业学院学报，2000，18(4)：65-68.

[2] 祝毓琥.机械原理[M]. 北京：人民教育出版社，1979.

[3] 张启先.空间机构分析与综合[M].北京：机械工业出版社，1980.

[4]华大年，唐之伟.机构分析与设计[M].北京：纺织工业出版社，1985.

[5] 黄 真.高等空间机构学[M].北京：高等教育出版社，2006.

[6] 谢存禧,李 琳.空间机构设计与应用创新[M].北京：机械工业出版社，2008.

[7] 华大年,华志宏.连杆机构设计与应用创新[M].北京：机械工业出版社，2008.

[8] C.H.Suh， C.W.Radcliffe. Kinematics and Mechanisms Design[M]. New York: John Wiley & Sons, 1978.

[9] 牧野洋,谢存禧,郑时雄.空间机构及机器人机构学[M].北京：机械工业出版社，1987.

[10] 王 铎,程 靳.理论力学[M].北京：高等教育出版社，2002.