平面上有限级随机Dirichlet级数的亏函数研究

杨 祺

(新疆师范大学数理科学学院,新疆乌鲁木齐830054)

曹月波

(石河子大学师范学院,新疆石河子832000)

关于随机函数亏值的研究,已经取得了许多研究成果[1-5]。对于有限级随机Dirichlet级数的亏函数,文献 [1]证明了全平面上有限级随机Dirichlet级数几乎必然没有亏函数。下面,笔者在随机变量满足一般的条件下,证明了平面上精确级为ρ(r)的随机Dirichlet级数几乎必然无任意精确级小于ρ(r)的亏函数①新疆师范大学优秀青年教师科研启动基金项目 (XJNU0816)。。

1 基本概念与引理

考虑Dirichlet级数:

式中,s=σ+it,σ,t∈ R,{bn}为复常数列,0=λ0＜λ1＜λ2＜… ＜λn＜… ＜+∞。若满足:

则级数(1)在全平面上是收敛与绝对收敛的,于是f(s)表示一整函数。记 f(s)的最大模为:

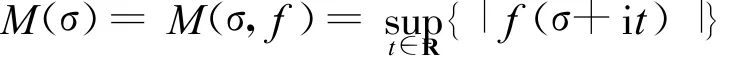
引理 1[6-7]对于有限 ρ级 Dirichlet级数(1),引进函数U(r)=rρ(r)(r=eσ),其中 ,ρ(r)在r ≥r0(r0＞0)上单调、分段连续,且满足并且当r＞r′0＞r0时,U(r)为r的增函数1。则称U(r)为级数(1)的型函数,ρ(r)为级数(1)的精确级.

引理2[6-7]设有限ρ级Dirichlet级数(1)满足条件(2),则有:

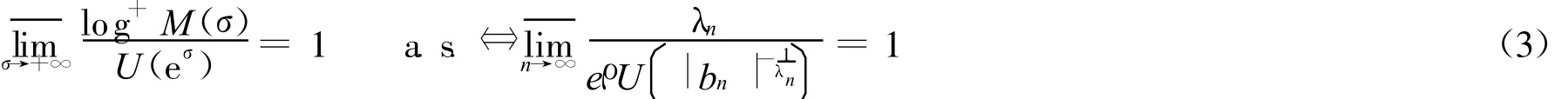
引理3[1,8]设函数 f(z)与 ψν(z)(ν=1,2,…,q)在|z|＜R ≤+∞内亚纯,ψν(z)互相判别,且T(r,ψν)=o{T(r,f)},则 :

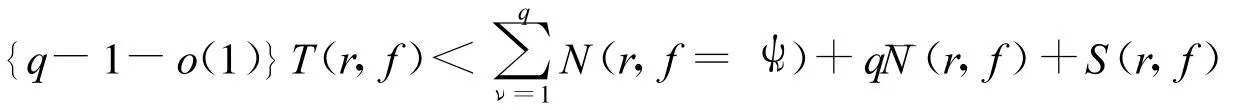
其中,当R=+∞时,S(r,f)=O{log(rT(r,f))},可能除去一列总幅长为有限的例外区间;当R＜+∞,除去r的一个集合E 0满足:

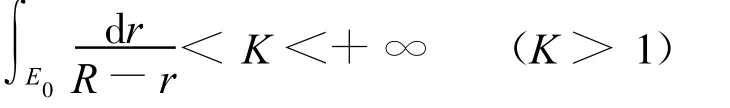
考虑与级数(1)对应的随机Dirichlet级数:

设{(Ψn,An,Pn)}是概率空间的无穷序列,是乘积概率空间,设{Xn(ωn)是空间上的独立随机变量序列,令

引理4[5]设{X n}是独立的随机变量序列,它满足 ∀n≥0,EXn=0,存在一个正数d,使得:

2 主要结果

定理1 若独立随机变量序列{Xn(ω)}满足式(5),并且

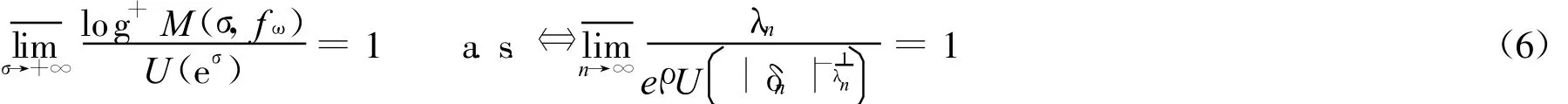
证明 用类似文献[6]中的方法易得。

定理2 若有限级随机Dirichlet级数满足定理1的条件,且

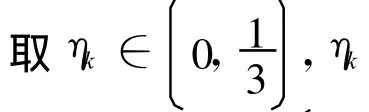
证明递减趋近于 0,Δ ＞0。令:

取正整数p充分大,令:

下面先证明对任意p+2个元素:

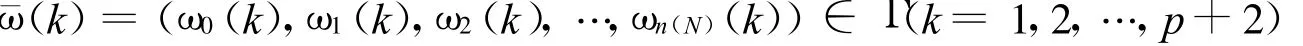
必存在k′,k″∈ {1,2,…,p+2}(k′≠k″)使得对任意 j∈ (n(1),n(2),…,n(N)},恒有:

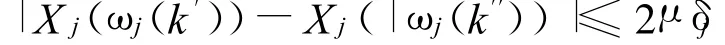
用反证法。假设上述不成立,则存在相应的p+2个随机级数:

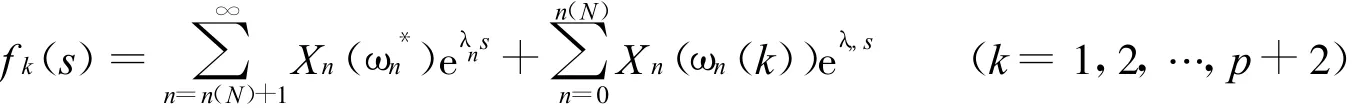
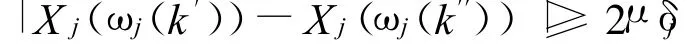
结合式(7)和式(8)有:

于是φk′≠φk″,这说明上面的p+2个亏函数互不相等,则由引理2,f至多能有p+1个不同的亏函数矛盾。

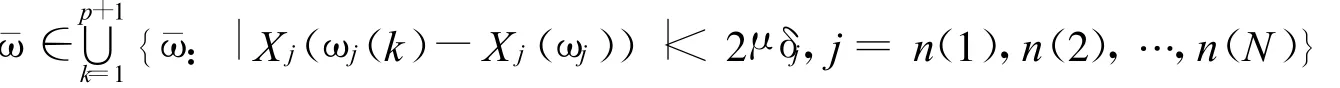
由引理4有:

这说明若 ω=(ω0,ω1,ω2,…)=(¯ω,=ω)∈ E=E(p,Δ,δ)⊂ Ψ。则:

于是由Fubini-Levi定理[3],并结合式(8)、(9)有:

因此P(E)=0。从而定理2得证。

[1]周俊英,孙道椿.Dirichlet级数的唯一性定理和随机Dirichlet级数的亏函数[J].华南师范大学学报,2006(1):36-42.

[2]余家荣,丁晓庆,田范基.Dirichlet级数和随机Dirichlet级数的值分布 [M].武汉,2004,52:98-100.

[3]孙道椿,黄立鹤.无限级随机Dirichlet级数 [J].华南师范大学学报,1998(4):87-93.

[4]孙道椿.随机幂级数的亏函数 [J].数学物理学报,1999,19(3):356-360.

[5]田范基.一般随机泰勒级数的例外函数[J].湖北大学学报,2002,24(3):203-205.

[6]陈聚峰,刘名生.有限级Dirichlet级数及随机Dirichlet级数 [J].数学物理学报,2005,25A(7):965-973.

[7]吴世轩,宁菊红.有限级Dirichlet级数[J].江西师范大学学报,2008,32(4):982-985.

[8]杨乐.值分布论及其新研究 [M].北京:科学出版社,1982.40-45. [编辑] 洪云飞