在eM-Plant环境下基于遗传算法的JSP仿真优化
2011-02-09王家海马云雷肖睿恒
王家海,马云雷,肖睿恒
(同济大学 机械工程学院,上海 201804)
0 引言
随着科学技术的发展,生产规模越来越大,复杂性越来越高,市场竞争越来越激烈,对企业的管理和生产过程的控制都提出了越来越高的要求。为了获得最大的经济利益,传统的,以经验为基础的生产调度方法已经不能满足现代生产的需求,如何科学有效的进行生产调度成为企业管理者面临的大问题。
生产调度问题是非常复杂的问题。通常是多约束、多目标、随机不确定优化问题。求解过程的计算量随问题的规模呈指数增长,已经被证明是NP完全问题[1]。其中作业车间调度问题(jobshop scheduling problem,JSP)问题是最困难的组合优化问题之一。本文正是想通过运用软件eM-Plant内置的GA(遗传算法)模块,对JSP问题进行初步的仿真和优化。
1 问题描述及建模
1.1 JSP问题数学描述[1]
设生产系统生产n个产品,表示为集合N={1,2,……,n},生产系统内有m台机器,表示为集合M={1,2,……,m},每个工件需要经过若干道工序加工完成,Oikq表示第i个工件的第k道工序在第q台机器上加工,其开始加工的时间和需要加工的时间为Sikq和Tikq;工件i的最后一道工序的开始加工时间和需要加工的时间记为Sieiq和Tieiq,工件i的投料时间和交货期是ri和di;Pi是工件的有序工序对[Oikp,Oikq]的集合,其中Oikp优于Oikq,Rq是使用机器q的所有工序Oikq的集合。如果目标函数为最小化最大完工时间,或者是最小完工周期,则JSP问题可以描述为:
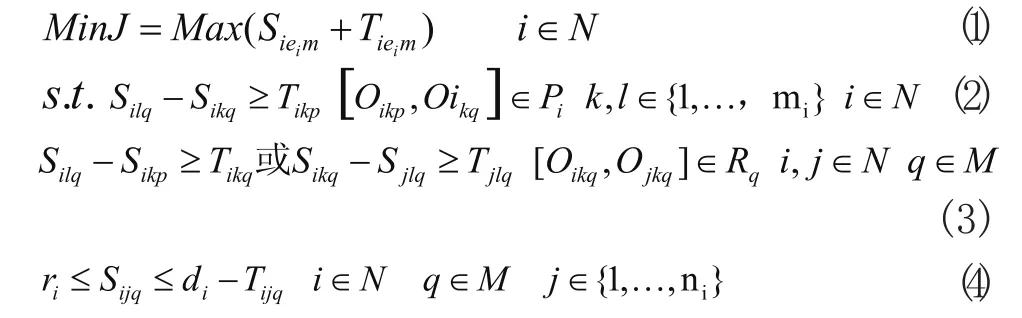
1.2 模型的建立
在笔者建立的作为演示的模型中,各项具体参数如下:
十种零件:J1,,J2,J3,J4,J5,J6,J7,J8,J9,J10。
四台机器:M1,M2,M3,M4
各零件的工序如表1所示。
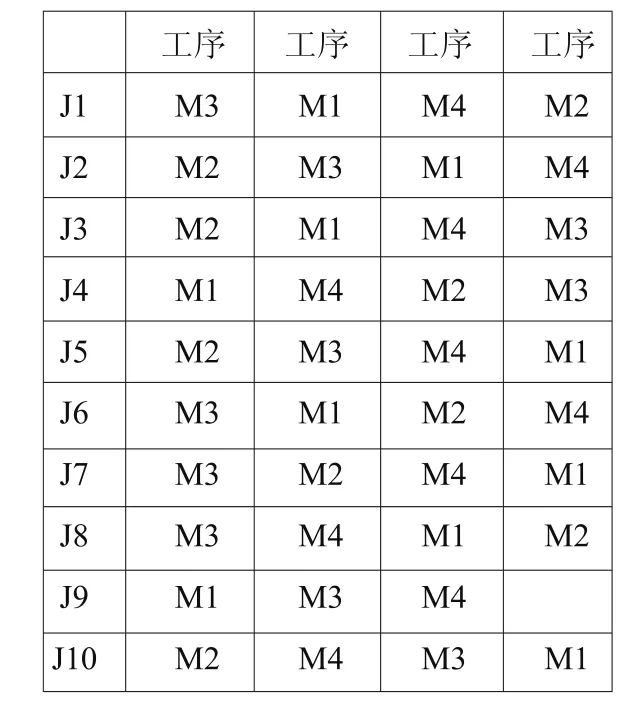
表1 工件加工工序
各机器在加工各零件的准备时间(秒):
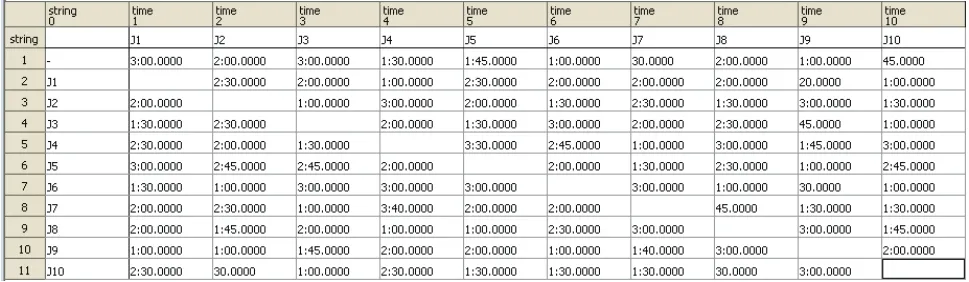
图1 M1的准备时间
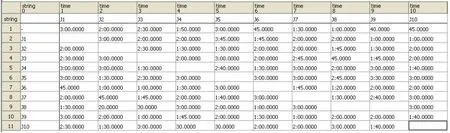
图2 M2的准备时间
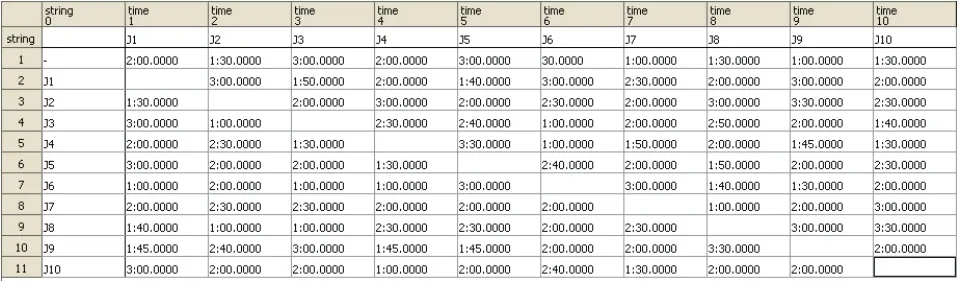
图3 M3的准备时间
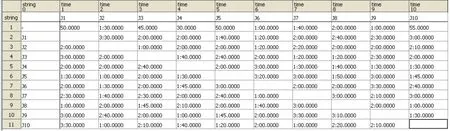
图4 M4的准备时间
在四台机器上的加工时间(分钟):
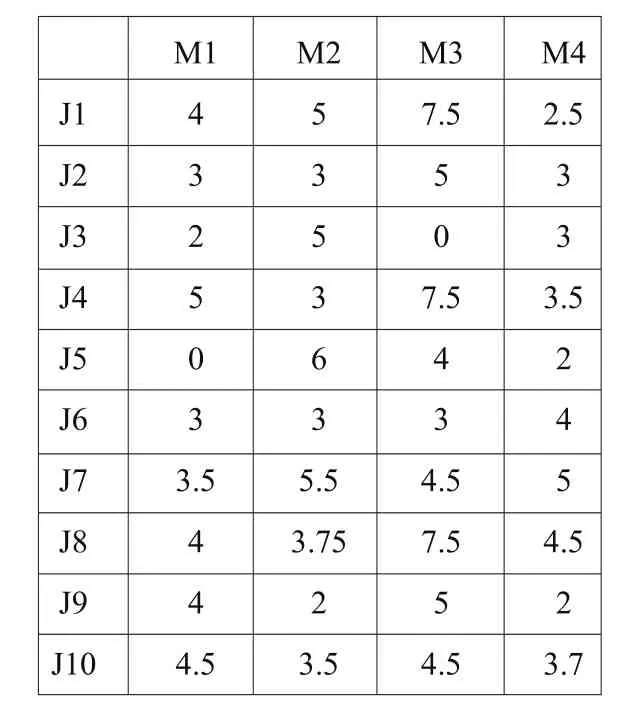
表2 各工件加工时间
模型如图5所示。
其中Delivery表式用来记录工件的加工顺序,SOP表是用来记录各个工件的工序,ProTime表用来记录各个机器加工各工件的时间,setTime表用来记录各机器在切换零件时的准备时间。
2 模型的仿真及优化
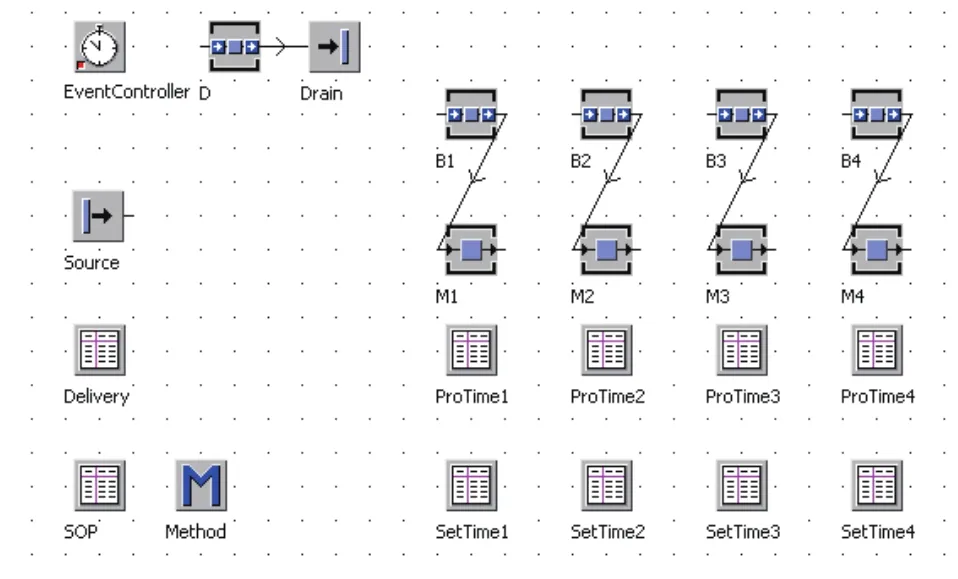
图5 JSP模型
2.1 模型的仿真结果
在模型建立完毕之后,笔者对此模型进行了仿真,工件进入系统的顺序是J1,J2,J3,J4,J5,J6,J7,J8,J9,10甘特图如6所示。
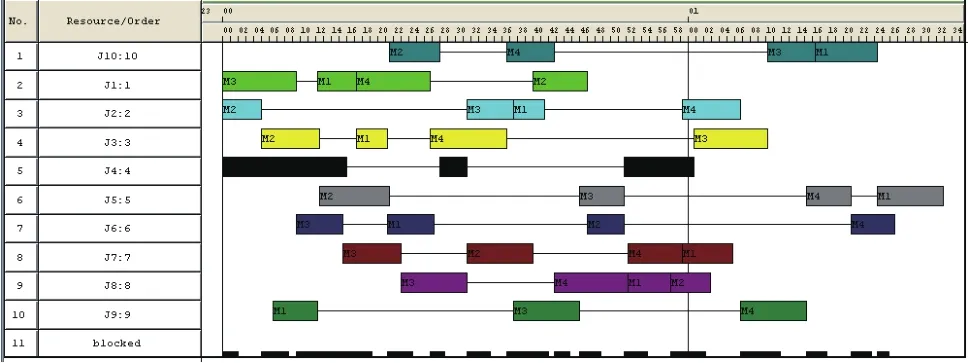
图6 未优化时的甘特图
总的加工时间是1:32:55。
2.2 模型的优化
eM-Plant为我们提供了GA模块进行对模型的优化,优化目标是使得仿真时间最短。JSP优化问题是典型的顺序优化问题,我们可以选择系统自带的GASequence工具和GAWizard结合来进行优化。鉴于系统帮助文档的参数值推荐,各参数设置如下[2]:
交叉概率:0.8
变异概率:0.1
代数:20
每代个体数量:10
优化后,零件进入系统的顺序是J10,J4,J6,J5,J8,J3,J9,J7,J1,J2,甘特图如7所示。
由优化后的统计图能看出,该问题由第一代时,平均的适应值为5820左右,经过十三代的遗传变异,适应值逐渐收敛,最后稳定在了4600左右,由此可见,该方法确实能有效的解决此类的问题。在优化之后,总的加工时间是1:17:20,比之前提高了15.5分钟,效率提高16.70%。

图7 优化后的甘特图
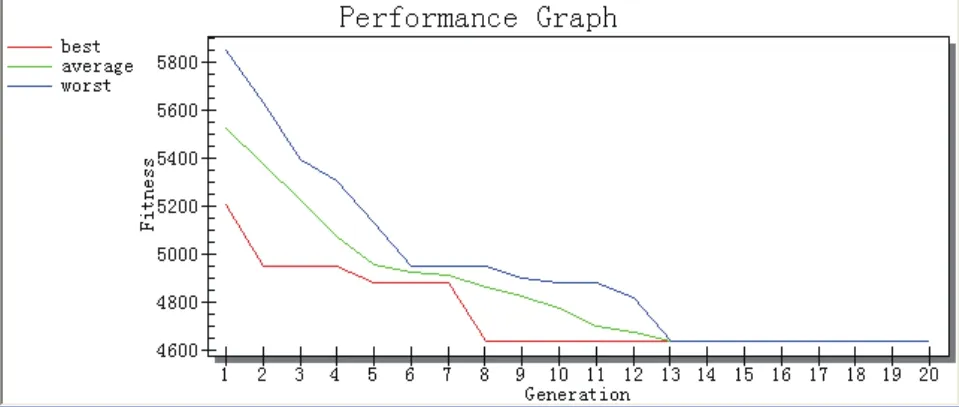
图8 优化结果
3 结束语
eM-Plant的GA模块简单易用,能初步的解决JSP问题,提高生产效率,但该模块也有明显的缺点:作为遗传编码的设计的重点,遗传编码的设计,在eM-Plant中是集成在GASequence中的,而eM-Plant中规定[2],其编码序列中中不能出现相同的基因,这就意味着,在处理多零件且每种零件不止一个的加工时,需要对同种零件的不同个体采用不同的表示方法,这显然增加了许多不必要的工作量。因此,笔者认为,在解决实际生产问题是,用外部代码进行遗传算法优化(比如C或者Matlab),只用eM-Plant的强大的仿真功能提供适应度函数的结果是更好的选择。
[1] 王万良,吴启迪.生产调度智能算法及应用[M].科学出版社,2007.
[2] Tecnomatix Plant Simulation Help.
[3] 刑文训,谢金星.现代优化计算方法[M].清华大学出版社,1999.
[4] 高玮玮.基于eM_Plant注塑模具制造过程的优化与仿真.苏州大学,2007.
