基于小波分解和相同尺度序列的神经网络短期电价预测
2011-02-08肖霖,张婧,曾鸣,董军
肖 霖,张 婧,曾 鸣,董 军
(1.重庆市电力公司 南岸供电局,重庆 400060;2.重庆市电力公司 市区供电局,重庆 400015;3.华北电力大学 能源与电力经济研究咨询中心,北京 102206)
目前常用的电价预测方法有时间序列法和神经网络法,主要根据大量的历史数据,找出电价序列的波动规律,从而建立预测模型进行预测[1—4]。小波变换具有滤波去噪功能,作为一种数据处理手段,首先被应用于负荷预测的研究[5]。在电价预测中,小波变换可以与时间序列法和神经网络法相结合,对电价样本分解后的各个子序列进行预测,通过重构各个预测结果得到最终预测电价[6—9]。
在现有研究的基础上,提出了基于小波分解和相同尺度序列相结合的电价预测方法,首先对负荷和电价原始数据进行多分辨率小波分解并剔除高频噪声信号,然后将相同尺度的负荷和电价子序列相结合,再根据该尺度子序列的时频特征有针对性地设计建立神经网络进行预测,最后将各尺度上的预测结果重构得到最终预测电价,并通过算例分析证明了该方法的实用性。
1 小波分解理论
1.1 小波分解原理
小波变换的概念由Morlet J于1984年首次提出,1989年Mallat S提出了多分辨率分解的概念,统一了在此之前的各种构造小波的方法,提出了二进小波变换的快速算法。多分辨率分解用小波函数和尺度函数对信号的低频概貌部分进行进一步分解,不考虑高频细节部分的分解。多分辨率分解在函数空间L2(R)内,将函数f描述为一系列近似函数的极限,每一个近似都是函数f的平滑版本,而且是越来越精细的近似函数,这些近似都是在不同尺度上得到的。设N为要分解的任意尺度,则f(t)在分解水平为N下的完全重构公式为
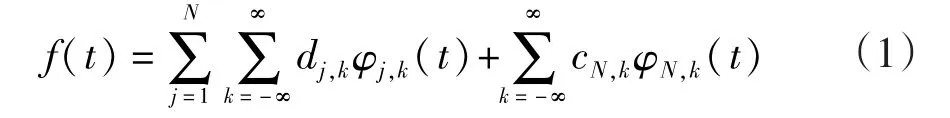
式中:j为尺度;k为平移因子;dj,k=〈f(t),φj,k(t)〉为小波展开系数;cN,k=〈f(t),φN,k(t)〉为尺度展开系数;φj,k(t)为小波函数;φN,k(t)为尺度函数;第1项为分解重构得到的各细节序列;第2项为概貌序列。
1.2 小波分解在电价预测中的应用
电价具有特殊的周期性,以天、星期等为周期波动,同时存在一定的非周期分量和随机分量。以3层分解为例,电价多分辨率小波分解的过程和子序列如图1和图2所示。多分辨率小波分解将部分周期性的电价分量、非周期分量以及低频随机电价分量投影到A3中,其他周期分量和随机分量分别投影到不同的尺度上。相对于A1,A3中含有高于尺度3的频率成分,但不含有介于尺度1—3之间的频率成分。由于不同尺度下的小波分量正交且无冗余,提供了带通滤波的良好工具,且可避免由各分量的关联性引起的分析困难。

图1 电价的多分辨率小波分解过程

图2 多分辨率小波分解后的电价子序列
2 短期电价预测模型
本文采用db5正交小波对历史电价序列和负荷序列进行分解。由于最终的预测电价是从不同尺度上子序列的预测结果重构得到的,而多次重构可能造成误差的累加,因此分解水平不宜过高。本文选择2尺度分解。当分解尺度为2时,概貌序列A2主要表现为日周期分量和半日周期分量,细节序列D2体现了其它周期分量和非周期分量,由不可测因素致使电价和负荷突变的随机噪声分量则集中在细节序列D1。在不考虑供应的情况下,负荷需求的波动是造成电价变化的直接原因。由于负荷波动相对于电价波动具有较强的规律性和较低的跳跃性,因此将分解后相同尺度的负荷和电价子序列相结合有助于利用神经网络挖掘潜在的电价变化规律,进而提高预测精度。预测模型的计算流程如图3所示。
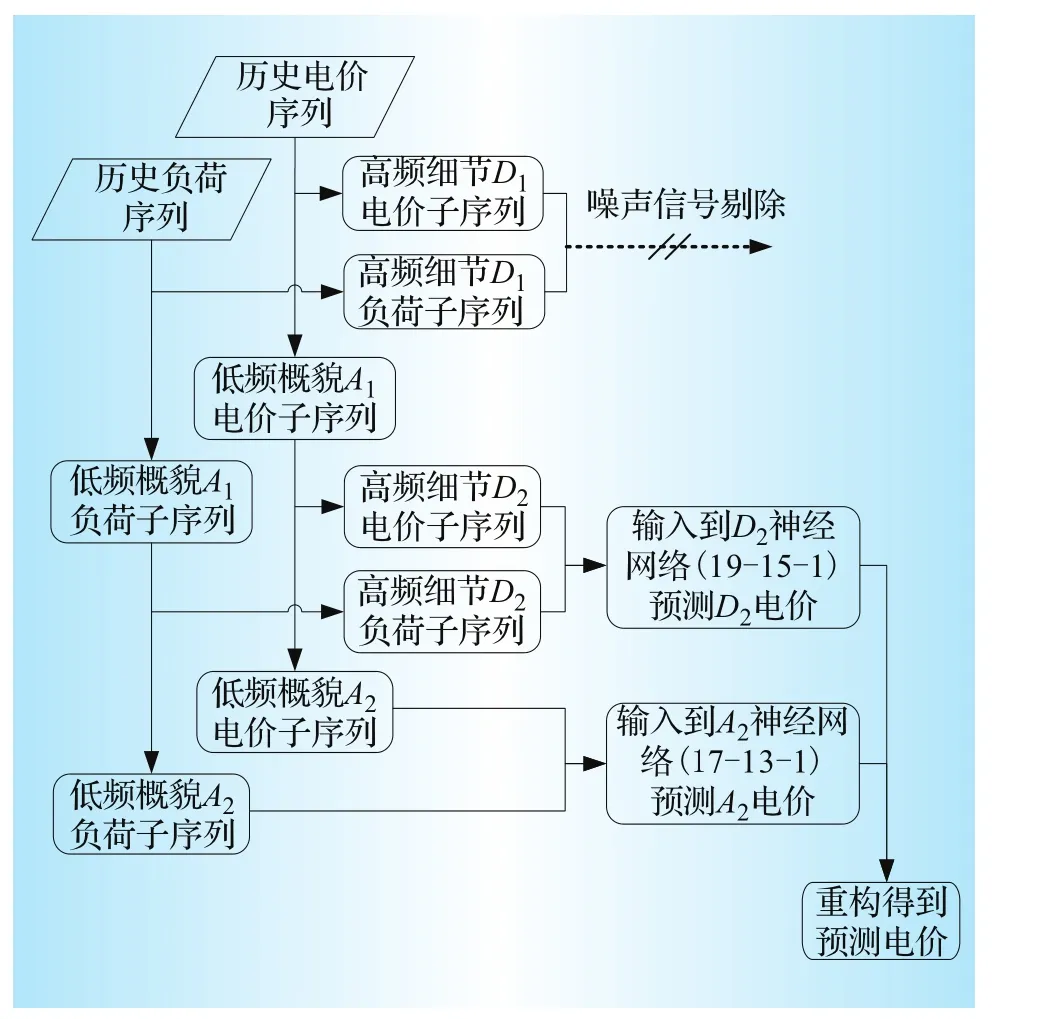
图3 预测模型计算流程
本文以历史电价和负荷数据作为神经网络预测的输入因素。事实上,在条件允许的情况下,在选择输入变量时可以将对电价影响作用不同的因素区别对待。例如:电价直接受供需因素的影响,因此可以将系统负荷容量、可用发电容量、市场供需比、必须运行率、竞价空间等作为直接影响电价的因素;气温、天气、节假日等只是直接影响需求或供给,而不对电价造成直接作用的因素可以作为电价的间接影响因素。对于直接影响因素和间接影响因素,可以采取不同的数据预处理方式。例如:对于温度因素可以设置敏感区间,当温度在常温范围内小幅变化时不考虑其对负荷和电价的影响,一旦温度上升或下降幅度过大进入敏感区间,则可能会影响用户的制冷或供热需求,从而影响电价。由于一天之内的温度变化相对较为缓慢,可以与概貌子序列相结合作为神经网络的输入变量,而不必与细节子序列相结合。
由于不同尺度的子序列具有不同的频率特性,因此可以对每一尺度的预测都分别建立BP神经网络模型,并针对该尺度所反映的波动规律有针对性的选择输入变量。例如:A2子序列随时间变化较为缓慢,且决定了大致的电价水平,因而输入变量的采集需要跨越较大时间间隔才能准确把握变化规律;D2子序列的波动较为频繁,虽然对电价的大体趋势没有直接影响,但却对价格尖峰的预测有很大的影响作用,因此需要在较短时间间隔内连续采集输入变量以体现该尺度上电价和负荷的变化趋势。本文对以上子序列分别建立BP神经网络进行预测,其网络结构如表1所示。
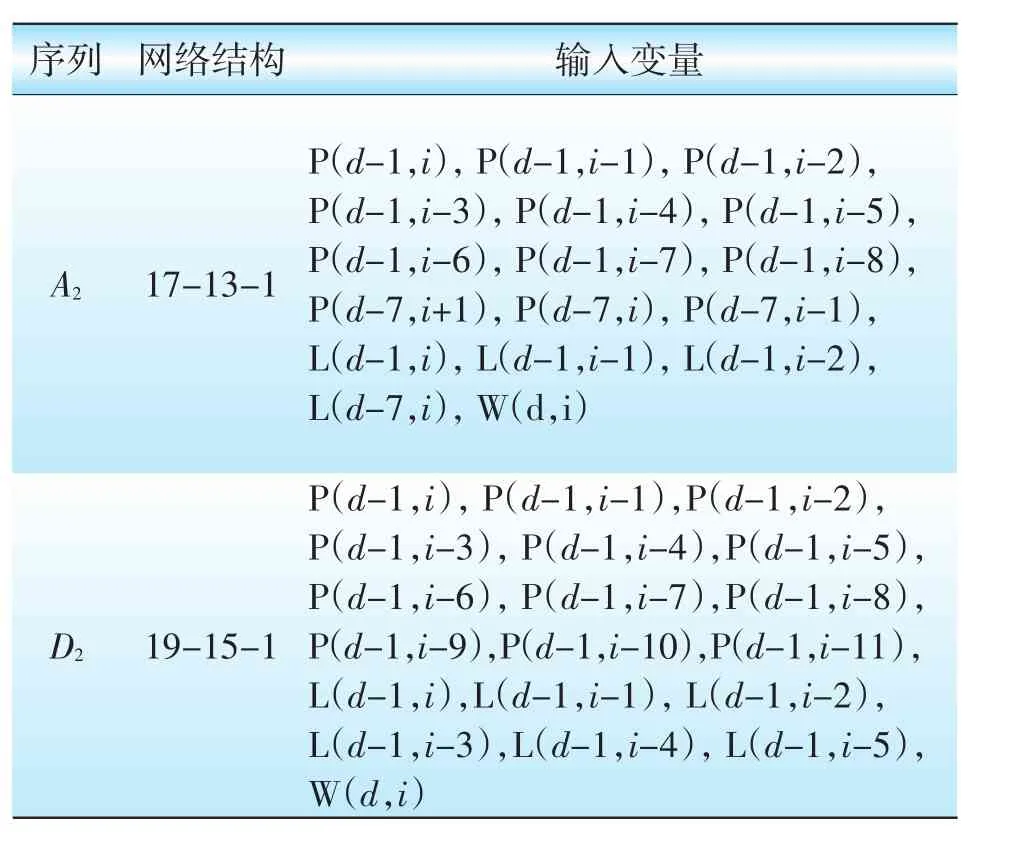
表1 各尺度子序列的BP神经网络结构
对于预测结果,可以采用平均绝对百分比误差(mean absolute percent errors,MAPE)度量预测电价的精度。由于实际电价中常出现0电价或接近于0的电价,本文采用改进的绝对百分比误差来度量。

式中:Pf,i为各时间点的预测电价;Pa,i为各时间点的真实电价。
3 算例分析
美国宾夕法尼亚-新泽西-马里兰(Pennsylvania-New Jersery-Maryland,PJM)电力市场是世界上最大的电力市场之一,由独立系统操作员(independent system operator,ISO)协调并确保市场的安全、经济、高效运营[10],其官方网站公开了规范完备的市场历史数据,为实证分析提供了数据基础。本文选取2007年2月至2008年2月的数据,具有较好的连续性和完整性,可以对提出的预测方法进行全面的检验。
假设有4个短期电价预测模型:模型1为本文提出的预测方法;模型2为传统的基于神经网络的预测方法;模型3为对电价进行单尺度小波分解,并将负荷分别与电价概貌序列和细节序列相结合进行神经网络预测的方法;模型4与模型1类似,但对电价和负荷均小波分解至3尺度。针对某一日d的某一时间点i的电价预测,选取d日i时之前1个月的历史数据用于神经网络训练。
2007年10月21日至2007年11月19日的电价预测结果如表2所示。模型2由于没有采用小波分解技术,单纯依靠神经网络模型难以准确把握电价的短期变化规律,预测误差较大。模型3对电价数据进行了小波分解,预测效果较模型2有所改善,但是由于模型3仅对电价数据进行了单尺度小波分解,没有剔除噪声成分,原始负荷数据和分解后的电价细节序列中均包含了噪声信号,因而不利于神经网络的训练和学习。另外,由于模型3没有对负荷数据进行同样分解,而是直接将负荷数据分别与时频特征不同的电价概貌序列和细节序列组成神经网络进行预测,因此预测误差高于模型1。
模型4与模型1在方法上类似,而且分解地更加深入。这虽然有利于突出各尺度子序列的时频特征,但最终的预测结果需要对3个不同尺度上的预测结果进行重构,而多次重构可能造成误差的累加,致使预测准确性降低。因此,模型1对电价和负荷进行2尺度分解,既通过小波的滤波功能剔除了多余的噪声信号,又避免了多次重构导致的误差累加,因而在电价预测中较为适用。由表2可知,模型1在这段时间内的预测表现整体较好,30天的MAPE平均值达7.61%。
为了更好地检验4种预测模型在各种市场环境下的适应性和有效性,选择PJM市场从2007年3月至2008年2月之间连续12个月的数据进行分析。经计算,4种模型全年滚动预测所得的MAPE平均值分别为8.64%、10.61%、9.34%和9.01%。将4种模型每天预测值的MAPE按照升序排列,可以得到误差持续曲线,如图4(a)所示。分析图4(a)可以发现,与其他几个模型相比,模型2的预测误差整体偏高,说明在神经网络短期预测的基础上引入小波分解技术有利于降低误差。模型3在预测误差较低时段的表现和模型1及模型4较为接近,但是在预测误差较高时,模型3的预测误差增长较为显著。图4(b)是对图4(a)中预测误差较高部分的局部放大。从图4(b)中可以看到,模型4的误差分布与模型1最为接近,但由于过度的分解可能导致重构误差的累加,因此模型4在抑制较高误差方面的表现不如模型1。在全年连续滚动预测中,模型1表现出了较好的适应性和有效性,一年中预测结果MAPE低于5%的有27天,低于10%的有273天,低于15%的有348天。

表2 预测精度对比

图4 各模型的全年预测误差持续曲线
4 结论
本文首先利用小波多分辨率分解提取电价和负荷序列中的不同频率成分,并剔除高频噪声信号,然后根据每个尺度的时频特征,加入对休息日和工作日的考虑,有针对性的设计建立BP神经网络模型,以相同尺度上的电价和负荷子序列作为输入变量进行电价预测,最后将各个尺度上的预测结果重构得到最终预测电价。算例分析表明,该方法可以将交织在一起的不同频率成分的混合信号有效地分解到不同尺度上,减少噪声干扰,准确提取电价和负荷的各种周期性特征。同时,负荷波动与电价相比具有较强的规律性和较小的跳跃性,因而相同尺度的电价和负荷子序列之间的结合有利于神经网络模型挖掘电价的潜在变化规律,进而改善短期电价预测的精度。在通过小波分解电价和负荷等序列用于预测时,既要充分体现数据基本的变化规律和滤去噪音,也要兼顾多个序列的重构可能会累积和放大预测误差。D
[1] RaulPino,José Parreno,Alberto Gomez,et al.Forecasting next-day price of electricity in the Spanish energy market using artificial neural networks[J].Engineering Applications of Artificial Intelligence,2008,21(1):53-62.
[2] Vahidinasab V,Jadid S,Kazemi A.Day-ahead price forecasting in restructured power systems using artificial neural networks[J].Electric Power Systems Research,2008,78(8):1 332-1 342.
[3] 栗然,崔天宝,肖进永.基于云模型的短期电价预测[J].电网技术,2009,33(17):185-190.
[4] Zhou M,Yan Z,Ni YX,et al.Electricity price forecasting with confidence-interval estimation through an extended ARIMA approach[J].IEE Proceedings of Generation,Transmission and Distribution,2006,153(2):187-195.
[5] 宋超,黄民翔,叶剑斌.小波分析方法在电力系统短期负荷预测中的应用[J].电力系统及其自动化学报,2002,14(3):8-12.
[6] 张显,王锡凡,陈芳华,等.分时段短期电价预测[J].中国电机工程学报,2005,25(15):1-6.
[7] 魏平,李均利,陈刚,等.基于小波分解的改进神经网络MCP预测方法及应用[J].电力系统自动化,2004,28(11):17-21.
[8] 张显,王建学,王锡凡,等.考虑多重周期性的短期电价预测应用[J].电力系统自动化,2007,31(3):4-8.
[9] 苏娟,杜松怀,李才华.基于多因素小波分析的神经网络短期现货电价预测方法[J].电力自动化设备,2007,27(11):26-29,33.
[10] Mandal P,Senjyu T,Urasaki N,et al.A novel approach to forecast electricity price for PJM using neural network and similar days method[J].IEEE Transactions on Power Systems,2007,22(4):2 058-2 065.
