市场环境下发电侧与需求侧备用资源联合优化
2011-02-08何艺,王健
何 艺,王 健
(1.广西电网公司 电力科学研究院,南宁 530023;2.华南理工大学 电力学院,广州 510640)
为保证电力系统的安全稳定运行,系统需要配置一定数量的备用容量。系统备用按备用响应时间可以分为瞬时备用、旋转备用(10min)、慢速备用(30min)和冷态备用(数小时)。备用容量的选取需要兼顾电力系统的可靠性和经济性2个方面。备用太少不能满足供电可靠性要求,过多又会降低经济性,造成不必要的资源浪费,所以合理的配置系统备用是电力系统应对各种功率缺额、保证安全经济运行的关键。
在双侧开放的市场环境下,发电侧备用容量(reserve capacity of generation side,RCGS)和需求侧可中断负荷(interruptible load,IL)都可作为系统的备用容量。电力系统中部分用户具有一定的负荷弹性和快速调控能力,紧急情况下能够在较短时间内(如:10min)切除部分负荷,相当于向系统提供了旋转备用。IL作为电力系统备用容量的一种形式,改变了单纯配置备用发电容量的传统思维模式,有利于能源的合理利用和备用容量的优化配置[1,2]。
许多国家和地区都鼓励可中断负荷参与辅助服务备用市场。以美国电力市场为例,包括加州ISO、纽约ISO、德州电力可靠性协会在内的各区域电力市场的辅助服务备用市场都有较成熟的市场架构和激励措施,通过各种形式和计划鼓励需求侧资源参与系统备用[3—5]。
2010年11月,国家发展和改革委员会等六部委联合印发《电力需求侧管理办法》,明确了电力需求侧管理工作的责任主体和实施主体,以及16项管理措施和激励措施,其中要求各级价格主管部门在具备条件地区实行可中断负荷电价等电价制度。办法的出台为我国可中断负荷相关理论和实践的开展,以及需求侧能源的利用给予了有力支持。
双侧开放市场下系统备用需要解决2个问题:①如何合理配置发电侧和需求侧备用资源;②如何协调系统备用的可靠性和经济性。文献[6]利用会计成本法建立发电侧备用容量的优化模型;文献[7]基于能量和备用容量市场联合优化决策方法,利用最优潮流求解用户加入旋转备用市场竞标的模型;文献[8]引入了风险的评估模式,提出预防控制和事故后控制的协调模型并进行优化;文献[9]根据效用无差异理论,利用存储理论概念建立最优备用容量的数学模型并运用决策论的算法求解;文献[10]对备用辅助服务市场中的IL招标数学模型进行了研究,该模型基于最优潮流算法,并考虑了诸如负荷电气位置、功率因数等因素;文献[11]运用最优潮流定量研究了需求弹性对最优备用容量的影响;文献[12]针对IL和电源备用容量服务效用上的差异,建立了两者同时参与备用市场的帕累托优化模型;文献[13]在备用实时市场建立了兼顾系统安全性和经济性的目标函数,并动态考虑了IL备用的报价行为以及实时节点电价的影响。
系统备用优化配置包括RCGS和IL这2种形式的备用容量,引入发电系统可靠性指标EENS,在EENS计算时考虑了IL作为备用容量的影响,对传统的可靠性指标EENS评估模型进行了重新修正计算。在满足一定的EENS指标、保证系统可靠性的前提下,建立电网公司最优购买策略模型和潮流模型,实现了系统的最优潮流和备用市场的联合优化,同时考虑了备用响应时间对系统安全性的影响。市场架构如图1所示。
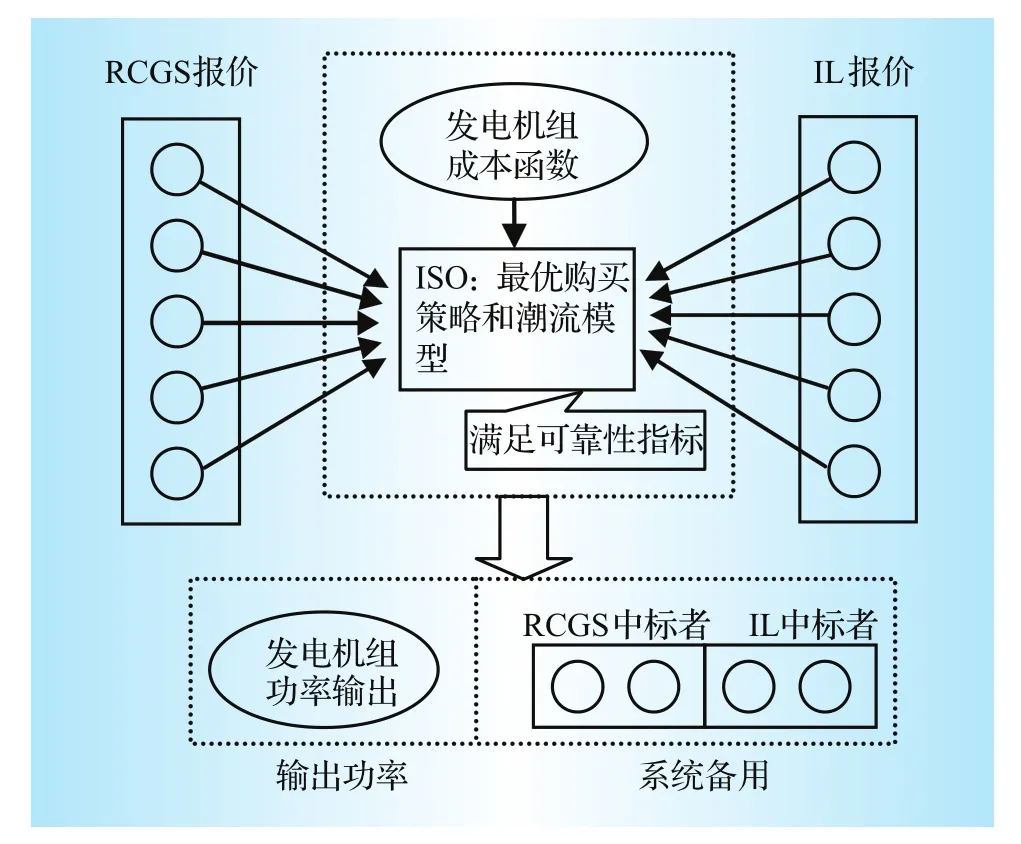
图1 双侧开放的备用市场架构
1 模型的建立
从系统运行管理者角度出发,建立发电成本与系统备用容量成本最少的目标函数、发电侧与需求侧共同参与辅助服务备用市场竞价的最优潮流模型。模型目标函数如式(1)所示,由发电成本、发电侧备用容量费用和需求侧中断负荷费用3部分组成。

式中:M表示参与竞价的发电机组;N表示参与竞价的可中断负荷用户;Pgm是发电机m的有功功率;Cm(Pgm)是发电机m的成本函数;ptgm是发电机组m提供备用的报价,美元/MW;Rtgm是竞价成功的发电机组m备用容量,MW;是IL用户n提供负荷中断的报价,美元/MW;是IL用户n中标的负荷中断量,MW;t是备用响应的时间,分别对应t=0min(瞬时备用),t=10min(旋转备用),t=30min(慢速备用)。这里仅考虑备用的容量成本,备用的电量成本是在事故发生或备用投入后才存在,在本模型中不作考虑。
(1)发电机组成本函数
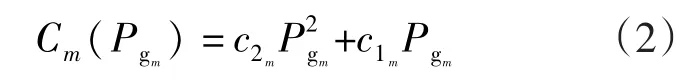
(2)约束条件
(a)潮流约束

(b)发电机有功和无功出力约束
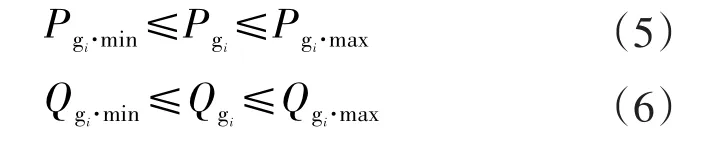
(c)节点电压约束
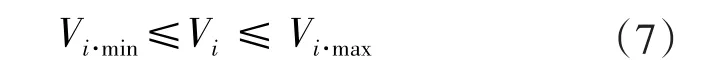
(d)发电机备用约束

式中:c2m、c1m是成本二次函数的系数;Pgi、Qgi是节点i上的有功和无功发电功率;Pdi、Qdi是节点i上有功和无功负荷功率;Vi是节点i的电压幅值;δij= δi- δj是i、j节点电压的相角差;是节点i的发电机有功出力上、下限;Qgi·max、Qgi·min是节点 i的发电机的无功发电功率上、下限;Vi·max、Vi·min是节点 i的电压上、下限;RRgm是发电机爬坡速率。
式(8)表示发电机m有功出力与备用容量之和应小于发电机m的装机容量;式(9)表示了备用容量的响应(尤其是10min旋转备用)应满足发电机爬坡速率的约束。
(e)可靠性指标约束
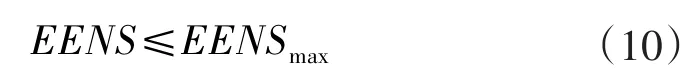
EENS是在一定期间内由于发电设备停运造成负荷停电而少供的电量,与系统备用容量和负荷状况密切相关。通过引入指标EENS,以小于最大值EENSmax作为约束条件,可以在优化系统运行费用的同时保证系统的安全可靠性。
发电机组能提供包括瞬时备用、10min旋转备用和30min慢速备用3种形式的备用,而IL用户要实现瞬时反应切负荷,中断成本太高,用户很难协调。故IL用户只提供相当于10min旋转备用和30min慢速备用这2种形式的IL备用。
2 电量不足期望值评估模型
2.1 传统EENS评估模型
解析法计算发电系统可靠性指标需建立2种模型:一种是由系统发电设备随机停运,根据停运容量而形成的系统状态空间模型,称为容量模型;另一种是负荷变化模型。将这2种模型结合即可得到表明电源充分性的系统综合模型[14]。
2.2 考虑可中断负荷的EENS评估模型
发电系统可靠性评估中考虑了IL的EENS曲线如图2所示,该曲线称为电量不足区域曲线。
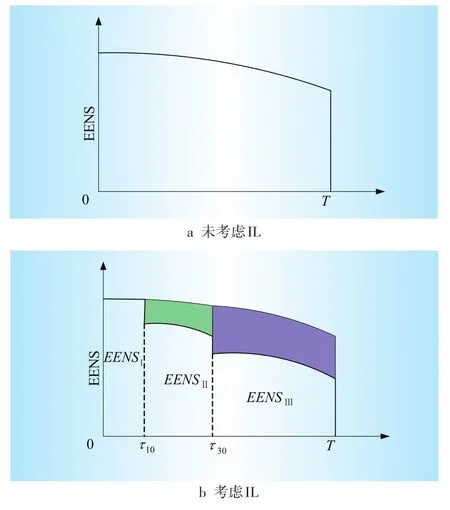
图2 时段T内系统EENS曲线
图2(a)表示没有IL参与下系统在时段T内的EENS,此时只有发电机组的备用容量参与备用市场;图2(b)则表示备用市场由于IL的参与有效降低了系统的EENS。由图2(b)可以看出,IL并不是在0时刻就能响应,而是经过了时间τ10(10min)后响应时间为10min的IL才能投入备用,EENSⅡ是发电机组和10minIL投入备用市场时系统的EENS,正上方的阴影部分表示由于10minIL投入备用而减少的EENS。同样经过时间τ30后响应时间为30min的IL也投入备用,EENSⅢ是发电机组、10min IL和30min IL投入备用市场时系统的EENS,其正上方的阴影部分是由于10min IL和30min IL投入备用而减少的EENS。
由于通信失灵、开关拒动等其他因素存在,IL不能100%成功响应,即IL存在响应失败的概率RIL。可把IL作为强迫停运率为RIL的发电容量加入到发电系统模型中,并通过式(10)计算累积概率,形成新的停运表,重新评估系统的EENS。
3 模型求解
最优购买策略的数学模型是包含连续变量和整数变量的非线性问题,采用改进遗传算法求解[15,16],具体步骤如下:
(1)编码采用混合编码方式,对发电机的有功和无功功率Pgi、Qgi,发电机备用容量Rtgm采用实数编码;对IL按响应时间分类型分别按报价进行排序,每类IL的中标个数采用整数编码。
(2)适应度函数为基因所对应的总费用,对于违反约束的情况,包括发电机最大功率约束、节点电压约束、发电机爬坡速率约束、可靠性指标约束等均采用惩罚的方式增加其基因对应的目标函数值,以更快淘汰违反约束的染色体。
(3)根据初始种群的值(除平衡节点外的发电机有功、无功功率)求解系统潮流,把得到的潮流解和各发电机备用容量、IL中断容量和报价代入适应度函数,并根据适应度进行排序。
(4)每隔10代保留适应度最好的5%染色体,其他染色体进行一次灾变。
(5)选择采用轮盘赌博的方式;交叉采用随迭代次数自适应法;变异采用变异率随个体适应度改变。
4 算例分析
以IEEE-30节点系统作为算例。IEEE-30节点系统共有6台发电机、20个负荷和41条线路[17]。发电机成本函数如式(2)所示,发电侧备用按瞬时备用、10min旋转备用、30min慢速备用分别进行报价,需求侧IL用户按10min响应时间和30min响应时间分别上报IL的容量价格,美元/MW,和中断容量,MW,节点电压幅值限制在0.94~1.06之间,研究时间段为240min。由于研究时段不长,故假定在研究时段内系统负荷保持不变。具体参数如表1—表3所示。

表1 发电机组参数

表2 发电机组备用容量报价

表3 可中断负荷参与备用容量报价
表2中发电机8和发电机11不参与备用市场或无法提供备用服务,发电机5无法提供瞬时备用。对于用户的负荷,电网公司或者中断、或者持续供电,不能进行部分的中断负荷和区段性的报价,因此只能采用0-1离散变量表示,如表3所示。响应时间为30min的IL用户报价总体低于10min的IL的报价,因为前者有更长的中断响应时间,能有充足的时间调整生产计划,最大化地减少停电损失。
下面分5种情况对模型进行计算和分析:①IL用户不参与备用市场,EENSmax=10MW;②IL用户参与备用市场,EENSmax=10MW,RIL=0;③IL用户不参与备用市场,EENSmax=5MW;④IL用户参与备用市场,EENSmax=5MW,RIL=0;⑤IL用户参与备用市场,EENSmax=5MW,RIL=0.05。优化结果如表4所示。
从表4可以看出,随着EENSmax的减少(即系统可靠性的提高),无论是系统备用容量还是总运行费用都是增加的。当系统可靠性要求不高时(①和②),只有少数IL用户在备用市场中标,对总运行费用影响不大。当进一步提高系统可靠性(EENSmax=5MW),通过③和④的比较可以看出,即使用户备用报价高于发电机,但相对于有限的发电侧备用资源,用户进入备用市场为系统提供了更多的备用容量选择,而且IL用户作为独立的备用容量加入发电容量模型,分散了停运表中的停运容量的概率,同等备用容量的情况下得到更好的可靠性指标,从而④的目标函数值、系统备用容量和备用费用支出等指标都优于③。⑤中考虑了IL的响应失败率RIL,需求侧IL容量不变,发电侧的10min旋转备用和30min慢速备用都略有增加,说明IL的响应失败率RIL对系统可靠性和备用最优购买策略是有影响的。
表5为情况③、④下各发电机中标的备用容量。③中由于每台机组瞬时备用容量有限(如表2所示),系统所需的瞬时备用由3台机组共同承担。根据机组备用报价,10min旋转备用应首先由发电机1承担,但机组爬坡速率的约束使得部分旋转备用不得不分给报价较高的发电机5和发电机13。30min慢速备用的报价中发电机2最低,但机组最大有功出力的约束使得一部分慢速备用得由发电机5承担。④中由于需求侧IL参与备用市场,发电侧的备用容量明显减少,备用市场的经济性和效率得到提高。
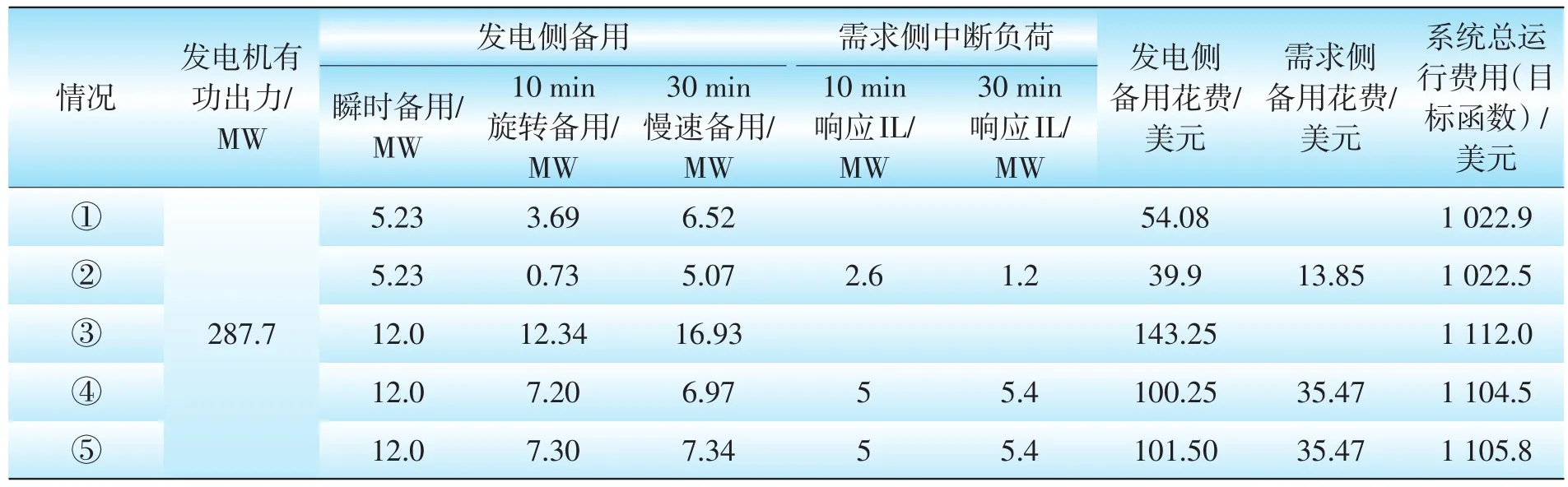
表4 系统经济效益比较
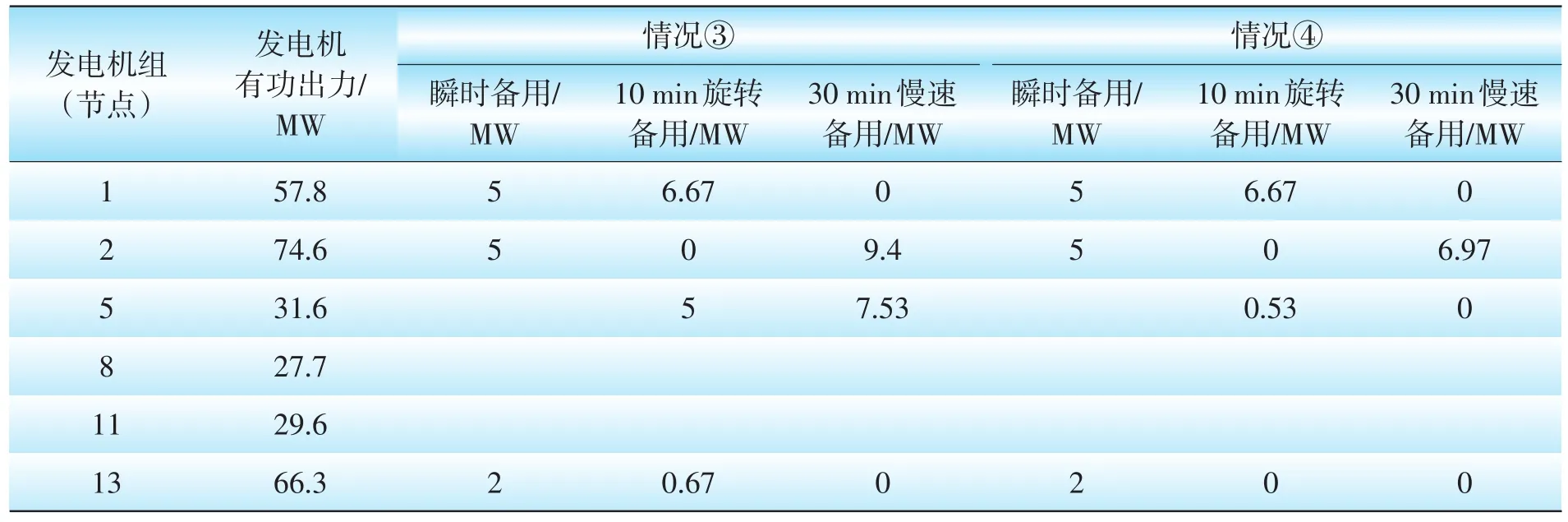
表5 发电机中标备用容量
5 结束语
发电侧和用户侧的积极参与是辅助服务市场建设的重要组成部分。文章建立起双侧开放的市场环境下最优潮流和备用市场的联合优化模型,在满足一定的EENS指标、保证系统可靠性的前提下,使系统的总运行费用最小,有效协调了安全性和经济性。结果表明需求侧IL进入备用市场为系统提供了更多的备用容量选择,有效降低了系统的总运行费,同时发电商对备用市场的控制力被减弱,市场的运营效率得到提高。
[1] 薛禹胜,罗运虎,李碧君,等.关于可中断负荷参与系统备用的评述[J].电力系统自动化,2007,31(10):1-5.
[2] 罗运虎,王勤,邢丽冬.系统备用容量优化问题综述[J].电网技术,2007,31(23):41-46.
[3] Price responsive load working group(NYISO).Status of NYISO demand response programs[R/OL].(2004-04-01)[2011-01-04].http://www.nyiso.com/public/webdocs/committees/bic_prlwg/meeting_materials/2004-04-01/prlwg_update_04012004.pdf.
[4] Departmentofmarketmonitoring(California ISO).Annu-al report on market issues and performance[R/OL].(2008-04-01)[2011-01-04].http://www.caiso.com/1f9c/1f9c8b49e9f0.pdf.
[5] Shen-Hsien Huang,Gonzalez-Perez C,Dumas J,et al.Grid security through load reduction in the ERCOTmar-ket[J].IEEE Transactions on Industry Applications,2009,45(2):555-559.
[6] 李晓军,谭忠富,王绵斌,等.考虑用户参与下电网公司购买备用的优化模型[J].电力系统及其自动化学报,2007,12(2):9-14.
[7] 潘雄,罗春雷,徐国禹.双侧开放市场中能量与备用容量的联合优化[J].电力系统自动化,2005,29(5):10-15.
[8] 罗运虎,薛禹胜,董朝阳,等.发电容量充裕性的混合优化[J].电力系统自动化,2007,31(12):30-35.
[9] 吴集光,刘俊勇,牛怀平,等.电力市场环境下最优备用容量的确定[J].电力系统自动化,2005,29(15):10-14.
[10] LeAnh Tuan,Kankar Bhattacharya.Competitive frame-work for procurement of interruptible load services[J].IEEE Transactions on Power Systems,2003,18(2):889-897.
[11] 王蓓蓓,李扬,万秋兰,等.需求弹性对系统最优备用投入的影响[J].电力系统自动化,2006,30(11):13-17.
[12] 葛炬,张粒子.可中断负荷参与的备用市场的帕累托优化模型[J].电力系统自动化,2006,30(9):34-37.
[13] Wang Jian,He Yi.Study onmodelof interruptible load to participate in reservemarket[C].Wuhan:Asia-Pacific Powerand Energy Engineering Conference,2009:1-4.
[14] 杨莳百.发电系统可靠性分析原理和方法[M].北京:水利电力出版社,1985.
[15] 王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
[16] 杨俊杰,周建中,喻菁,等.一种求解大规模机组组合问题的混合智能遗传算法[J].电网技术,2004,28(19):47-50.
[17] Alsaco,Stott B.Optimal load flow with steady-state secu-rity[J].IEEE Transactions on Power Apparatus and Sys-tems,1974,93(3):745-751.

