OFDM系统中的一种低复杂度带状ICI抑制算法

陈东华，仇洪冰

(1. 华侨大学信息科学与工程学院 福建 厦门 362021; 2. 西安电子科技大学通信工程学院 西安 710071;3. 桂林电子科技大学信息与通信学院 广西 桂林 541004)

OFDM系统中的一种低复杂度带状ICI抑制算法

陈东华1,2，仇洪冰1,3

(1. 华侨大学信息科学与工程学院 福建 厦门 362021; 2. 西安电子科技大学通信工程学院 西安 710071;3. 桂林电子科技大学信息与通信学院 广西 桂林 541004)

针对时变信道OFDM系统中的子载波间干扰(ICI)抑制问题，基于时变信道频域响应矩阵(CFR)的带状近似，提出一种低复杂度双迭代均衡方案。通过调整CFR矩阵的带宽大小，有效实现了性能和复杂度之间的良好折中。在检测过程中，首先利用线性ICI抵消降低了由于CFR矩阵的带状近似造成的性能恶化，其次通过迭代软干扰抵消检测算法来获得由信道时变带来的多普勒分集增益。理论分析和仿真结果表明，同传统线性最小均方误差时变信道均衡算法相比，该算法同时具有性能和复杂度的优势。

均衡器; 子载波间干扰; 正交频分复用; 时变信道

在高速移动通信中，无线信道的时变引起的多普勒频移会破坏OFDM系统子载波之间的正交性，导致子载波间干扰(ICI)并恶化系统性能[1]。

目前，抑制OFDM系统子载波间干扰的主要方法有频域均衡[2-3]、时域均衡[4]、ICI自抵消[5-6]等。文献[2-3]基于信干噪比最大化排序进行频域均衡，需要复杂的矩阵求逆，且需要大量的排序操作。文献[4]在时域上进行每子载波均衡，复杂度仍较高，且ICI自抵消方案以牺牲频率利用率为代价。根据时变产生的ICI主要来自相邻的子载波，忽略间隔较远的子载波的ICI。文献[7-10]分别提出了几种低复杂度ICI抑制算法。文献[7]提出低复杂度带状MMSE线性均衡器(BLE)，BLE通过带状矩阵的LDL分解来降低矩阵求逆的复杂度，其复杂度与子载波数呈线性关系，但是带外被忽略的ICI会带来均衡器的误码率地板效应。文献[8]提出单抽头均衡结合部分ICI抵消的迭代算法，但单抽头均衡器的性能受ICI的影响较大。文献[9-10]提出基于时域加窗的ICI抑制算法，该方法需要已知精确的时变信道多普勒频移，但实际中很难得到该参数的精确估计。本文根据ICI的分布随子载波间隔增大而逐渐减小的现象，提出一种新的迭代ICI抑制算法，该算法包含两级，第一级进行低复杂度带状LMMSE均衡，并利用检测的符号对带外ICI进行干扰抵消以消除带外ICI对带内信号的影响；第二级利用带外ICI抵消后的接收信号执行带内软干扰抵消均衡，以进一步抑制带内ICI。该算法能有效降低带外ICI引起的地板效应，且复杂度与性能之间可以实现折中。

1 ICI分析

2 迭代ICI抑制

给定CFR矩阵H，接收机可按如下LMMSE准则均衡得到发送信号的估计：

图1 CFR矩阵的带状近似示意图

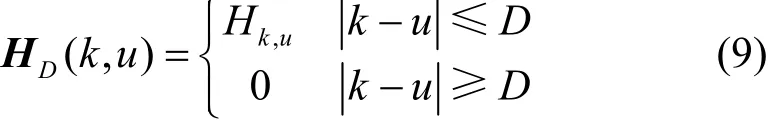
定义近似后的频域信道响应矩阵为HD，其第(k,u)个元素可表示为：即HD由H的主对角及D个上下对角线元素构成。基于此，文献[7]提出用带状矩阵HD取代H进行LMMSE均衡，即：

图2 带状矩阵的分割示意图

2.1 第一级迭代

第一级的每一次迭代分为两步，首先进行带内低复杂度带状均衡得到初始均衡值；其次，用均衡后的判决输出ˆs进行带外ICI抵消。第i次迭代的数学表达式为：

式(11)可利用带状矩阵的LDL分解来降低矩阵求逆的复杂度。利用带外ICI抵消后的接收信号(i+1)y再进行带状均衡，依次迭代直到收敛或达到预设的最大迭代次数。迭代过程的第一步可以看作是按最小均方误差准则的带内ICI抑制，第二步是带外ICI消除。其中，带内和带外带宽D1和D2可根据复杂度及性能要求灵活调整。

2.2 第二级迭代

经第一级迭代后，接收信号中带外ICI的影响得以降低，如果 s = sˆ，则考虑的带外ICI项都被抵消，接收信号仅包含带内ICI，不再受到带外ICI的影响，因此，利用第一级得到的接收信号，第二级只需在带内执行ICI抑制以抑制带内ICI的影响。迭代软干扰抵消LMMSE均衡[9-12]是一种有效的多符号分离算法，第二级中，用该算法执行带内ICI软抵消进一步抑制了ICI的影响。

当所有N个子载波估计以及它们的先验信息更新完毕后，利用更新的先验信息重新按式(13)和式(14)得到新的子载波估计，以此类推进行迭代检测，直到收敛或达到预设的最大迭代次数。

2.3 复杂度分析

3 仿真分析

图3给出了本文算法在D1=2和D2=6时的误比特率(BER)性能曲线，并给出了D=12时的带状LMMSE均衡算法的BER性能曲线。由图可见，经过第一级迭代，带外ICI得到抑制，性能得到改善；第二级迭代进一步抑制带内ICI。经两级迭代后，带内带外ICI同时得到抑制，性能有了明显提高。此时本文算法比D=12时的带状LMMSE均衡算法节省了3%的复乘运算，因此同传统带状LMMSE均衡算法相比，两级迭代均衡算法以更低的复杂度获得了更好的系统性能。

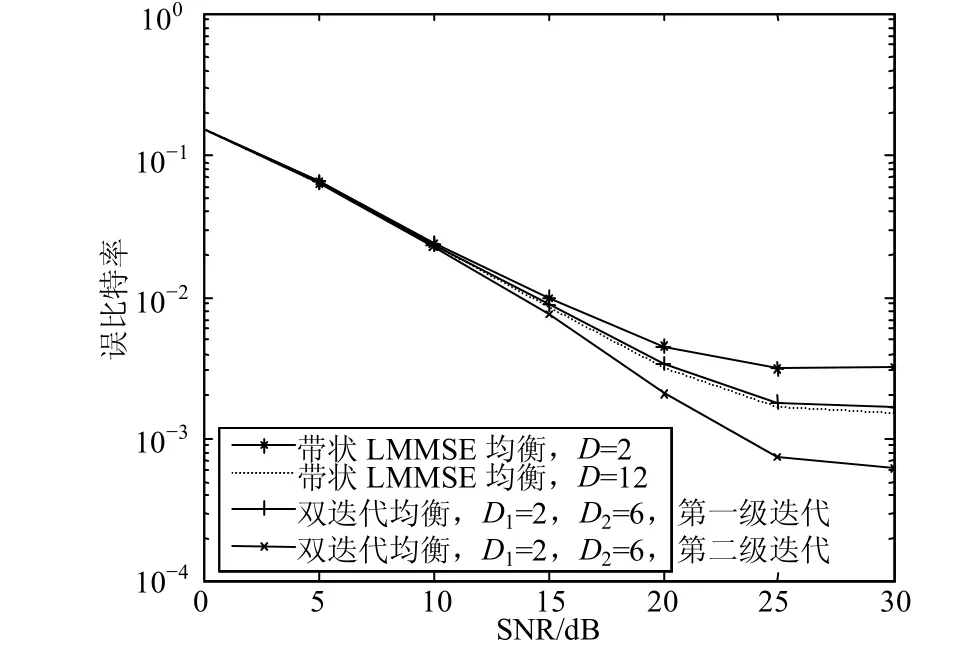
图3 本文算法与带状LMMSE均衡算法的性能比较

图4和图5分别给出了本文算法在带内外带宽分别为D1和 D2=N−D1- 1时系统的BER性能，即带外ICI包含除带内的所有ICI。图4和图5分别对应D1= 2 和D1=4的情况，与图3比较，由于考虑了更多的带外ICI，性能得到显著的提高。该两图还给出了传统LMMSE(全LMMSE)均衡算法的性能曲线。仿真结果表明，本文算法明显优于传统LMMSE均衡算法，这是由于信道时变引起ICI的同时，使得某一发射子载波的能量分散在各接收子载波上，意味着信道的时变带来了时间分集作用，因此，通过在每一次迭代过程中逐步抵消ICI，使得带状LMMSE均衡器能充分利用时间分集增益来提高均衡性能。全LMMSE均衡器虽然考虑了所有ICI，但全LMMSE均衡算法是在MSE最小准则下进行的ICI抑制，在严重的子载波间干扰下，时间分集效应得不到有效利用，因此本文迭代算法能获得比全LMMSE均衡器更好的均衡性能。该情况下本文的算法复杂度为 O (N2)，传统LMMSE算法的复杂度为 O (N3)，因此相对于传统ICI抑制算法，本文算法同时具有复杂度和性能的优势，而且CFR矩阵的带内外带宽可以灵活调整，可实现复杂度与性能之间的折中。

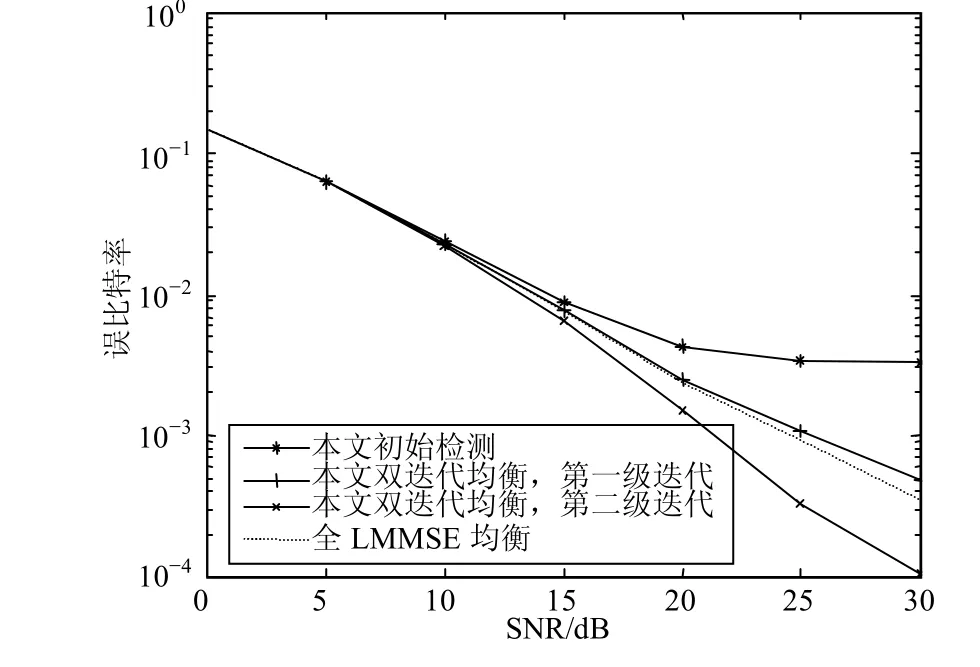
图4 D1=2，D2=N−D1−1时系统的性能

图5 D1=4，D2=N−D1−1时系统的性能

4 结 束 语

本文针对时变信道环境下OFDM系统的子载波间干扰抑制问题，根据时变信道CFR矩阵中非对角线信道响应值反应ICI功率的大小，ICI功率随对角线距离的增大而逐渐减小的现象，提出了一种两级迭代ICI抑制算法，该算法能有效地提高系统性能，具有较低的实现复杂度，并且根据复杂度与性能的要求，该算法可实现两者之间的折中，便于系统实现。

[1]HIJAZI H, ROS L. Polynomial estimation of time-varying multi-path gains with intercarrier interference mitigation in OFDM systems[J]. IEEE Transactions on Vehicular Technology, 2009, 58(1): 140-151.

[2]CHOI Y S, VOLTZ P J, CASSARA F A. On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels[J]. IEEE Transactions on Communications, 2001, 49(8): 1375-1387.

[3]CAI X, GIANNAKIS G B. Bounding performance and suppressing inter-carrier interference in wireless mobile OFDM[J]. IEEE Transactions on Communications, 2003,51(12): 2047-2056.

[4]GUPTA P, MEHRA D K. A novel technique for channel estimation and equalization for high mobility OFDM systems[J]. Wireless Personal Communications, 2009, 10:613-631.

[5]ZHAO Y, HAGGMAN S G. Intercarrier interference self-cancellation scheme for OFDM mobile communication systems[J]. IEEE Transactions on Communications, 2001,49(7): 1185-1191.

[6]秦文, 彭启琮. OFDM系统中基于符号变换的ICI自消除改进方法[J]. 电子科技大学学报, 2008, 37(5): 641-644.

QIN Wen, PENG Qi-cong. Improved ICI self-cancellation scheme for OFDM system based on symbol transform[J].Journal of University of Electronic Science and Technology of China, 2008, 37(5): 641-644.

[7]RUGINI L, BANELLI P, LEUS G. Simple equalization of time-varying channels for OFDM[J]. IEEE Communications Letters, 2005, 9(7): 619-621.

[8]LI R, LI Y, VUCETIC B. Iterative receiver for MIMO-OFDM systems with joint ICI cancellation and channel estimation[C]//Proceedings of IEEE Wireless Communications and Networking Conference. Las Vegas,USA: IEEE Press, 2008: 7-12.

[9]FANG K, RUGINI L, LEUS G. Low-complexity block turbo equalization for OFDM systems in time-varying channels[J].IEEE Transactions on Signal Processing, 2008, 56(11):5555-5556.

[10]SCHNITER P. Low-complexity equalization of OFDM in doubly selective channels[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 1002-1011.

[11]TUCHLER M, SINGER A C, KOETTER R. Minimum mean squared error equalization using a priori information[J]. IEEE Transactions on Signal Processing,2002, 50(3): 673-83.

[12]MOLISH A F, TOELTSCH M. Iterative methods for cancellation of inter-carrier interference in OFDM systems[J]. IEEE Transactions on Vehicular Technology,2007, 56(4): 2158-2167.

编 辑 张 俊

Low-Complexity Banded ICI Mitigation Scheme for OFDM Systems

CHEN Dong-hua1,2and QIU Hong-bing1,3

(1. College of Information Science & Engineering, Huaqiao University Xiamen Fujian 362021;2. School of Telecommunications Engineering, Xidian University Xi’an 710071;3. School of Information and Communication, Guilin University of Electronic Technology Guilin Guangxi 541004)

Aiming at mitigating intercarrier interference (ICI)caused by channel time variation in orthogonal frequency division multiplexing (OFDM)systems, a low-complexity doubly iterative equalization scheme is proposed by exploiting the approximately banded structure of channel frequency response (CFR)matrix. The scalability of band size of CFR matrix enables a good tradeoff between performance and complexity. In this scheme, a linear ICI canceller is used to reduce performance degradation caused by the band approximation of CFR matrix, and an iterative equalizer with soft interference cancellation is employed to gain the Doppler diversity induced by channel time variation. Theoretic analysis and simulation results indicate that the proposed technique has both performance and complexity advantages over the classic linear minimum mean square error (MMSE)equalizer in time varying channels.

equalizers; intercarrier interference; orthogonal frequency division multiplexing; time varying channels

TN911.5

A

10.3969/j.issn.1001-0548.2011.03.008

2009- 12- 02;

2010- 12- 10

国家自然科学基金(60962001)

陈东华(1977- )，男，博士生，主要从事宽带无线数字通信方面的研究.