Watterson信道下能量检测性能研究
2011-02-07闫江涛
闫江涛
(桂林电子科技大学 信息与通信学院,广西 桂林 541004)
0 引言
无线电频谱资源由频谱资源管理部门划分为两类:授权频段和非授权频段,非授权频段资源有限,但承载业务量不小,而授权频段的频谱利用率则不高。特别是对于3~30 MHz的短波波段,信道格外拥挤,且干扰严重。因此,必须找到一种有效的途径来提高频带利用率和抗干扰能力。
感知无线电(Cognitive Radio,CR)技术被认为是解决上述问题的最佳方法。它能够通过感知周围无线电磁环境,进行交互所获取的无线环境知识,调整传输参数(如载波频率、调制方式等),实现无线传输能力[1]。这样不仅可以实现高度可靠的通信,还可以通过感知频谱空洞提高频谱利用率。
如何检测空闲频谱是感知无线电中的关键技术之一,频谱检测技术方法多样,要求能够快速准确地检测到频谱空洞。其中能量检测算法实现要简单,可在无任何先验信息情况下通过信号能量进行检测,但如果信道存在衰落、阴影和噪声不确定性等影响时,能量检测的性能较差[2]。对于短波信道,其不仅存在衰落而且存在多径延时。本文针对Watterson短波信道模型,通过分集接收和提高观察时间的方法对能量检测方法进行改善,提高了检测概率。
1 Watterson信道模型
短波信道是典型的时变色散信道,采用的是多径瑞利衰落模型。其中Watterson模型是一个窄带信道模型,不适合于宽带信道描述与应用,在有限的带宽(10 kHz)和足够短的时间(10 min)可以近似平稳并用一个静态模型来描述。目前Watterson模型在大多数的情况下能够较好地反映出短波信道的特性,信道冲激响应[3]表示为
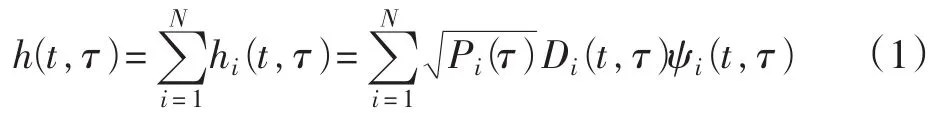
式中:h(t,τ)是第i条传播路径的冲激响应;t和τ分别是时间和传播延时;Pi(τ)表示第i条传播路径的延时功率谱,代表信道的脉冲响应是时间延迟功率谱;Di(t,τ)描述了每条路径的多普勒频移特性;ψi(t,τ)是随机调制函数,表现了短波信道的瑞利衰落现象。其信道模型的时变频率响应[4]可以表示为
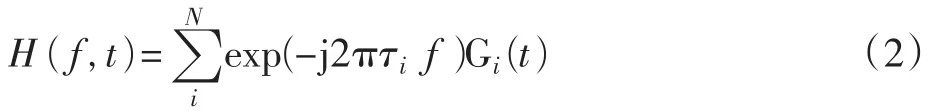
式中:N表示总路径条数;τi表示第i条路径的延迟时间;Gi(t)为随机过程,即
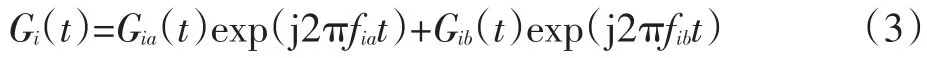
式中:Gia(t)和Gib(t)是两个相互独立的复高斯各态历经随机过程,它们彼此是零均值而且相互独立的正交分量。其包络服从瑞利分布,相位服从均匀分布。Gi(t)反映出了信道的时变色散,其谱密度函数为
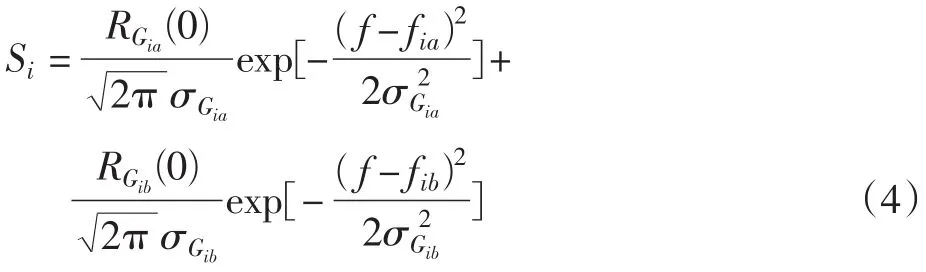
式中:RGia(0)为Gia(t)的自相关函数;σGia和σGib决定了第i条路径的多普勒频扩;fia和fib决定了第i条路径的多普勒频移。
2 能量检测模型
传统的能量检测算法如图1所示。先将信号通过滤波器滤除带外噪声和邻近信号,然后经过模数转换、平方器求出信号功率得到检测统计量Y,将其与预设门限值进行比较。当检测统计量Y大于门限值时,判定该频段存在第一用户,感知用户不能使用该频段;否则,判定该频段上仅有噪声,感知用户可以使用该频段。

图1 传统能量检测算法
当信道为非衰落的AWGN信道时[5],能量检测下的虚警概率和检测概率的表达式分别为
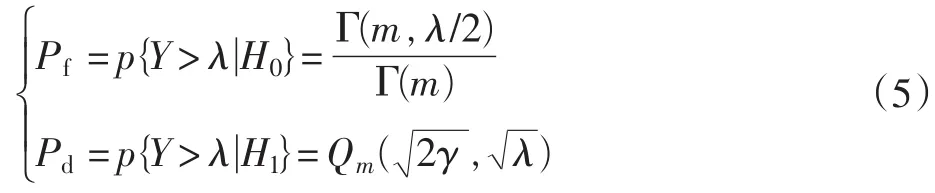
式中:Γ(.,.)表示不完整的伽马函数;Q()为一般的Mar⁃cum Q函数;m为观察时间与感兴趣的带宽的乘积。
当为衰落信道[6]时,信道幅度增益随信道衰落变化,信噪比的概率密度函数为fγ(x)时,平均检测概率为
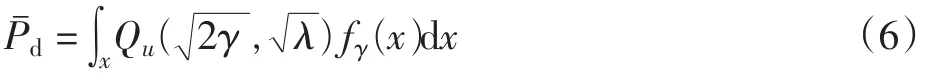
若为瑞利衰落信道,信噪比γ的概率密度函数为

这时,平均的检测概率为
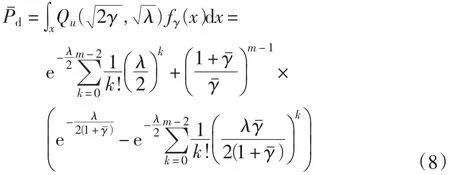
可以看出,传统的能量检测算法存在一个很严重的问题,特别是在低信噪比的环境中,当信道存在衰落、阴影和噪声不确定性等影响时,性能明显劣于AWGN下的检查性能。
然而,Watterson模型是在瑞利衰落模型的基础上建立的,为了解决在衰落信道下能量检测低的缺陷,这里主要研究了采用多天线分集接收的方法。这里在Watter⁃son信道下分别对采用平方律合并(SLC)、独立联合判决(MA)的能量检测算法进行了仿真和数据分析研究。
2.1 平方律合并[6]
平方率合并方法将每根天线上得到的检测统计量经过平方、积分得到的{}yi以相等的权重合并成新的检测统计量这里给出了此时的虚警概率和检测概率
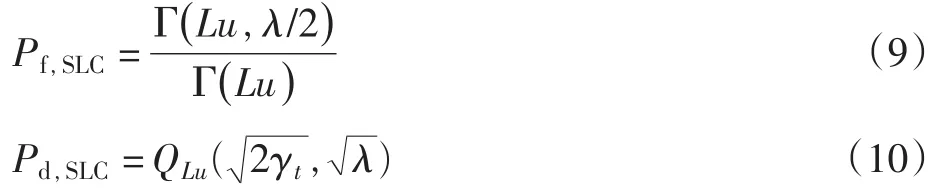
2.2 独立联合判决[7]
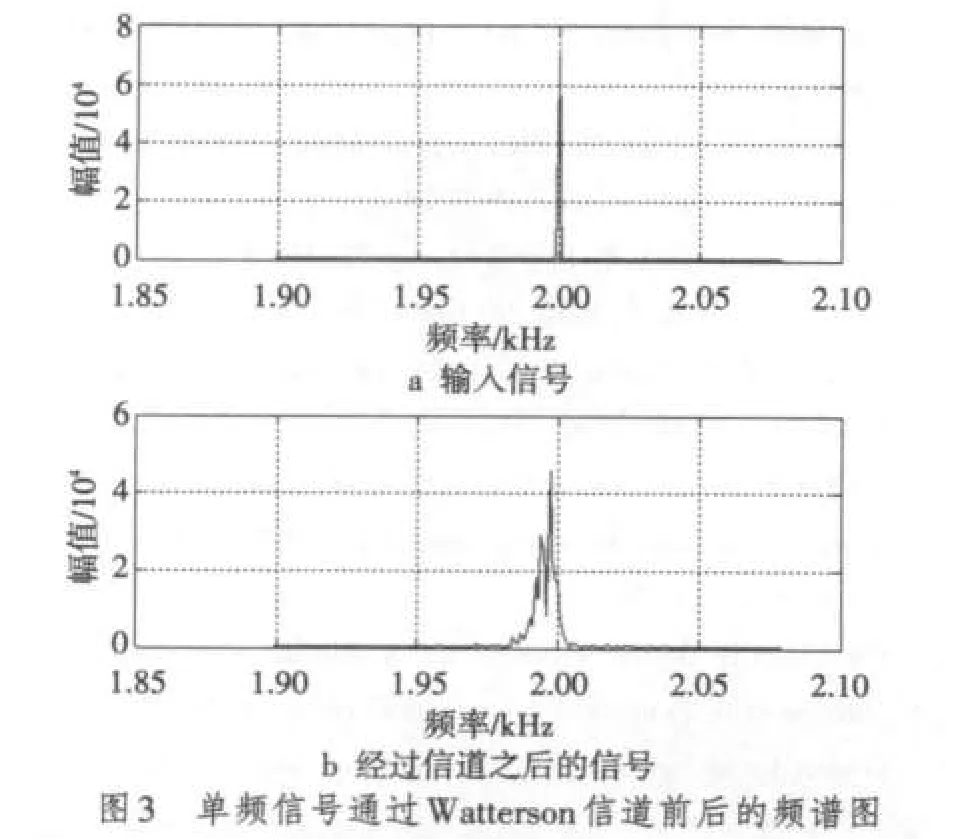
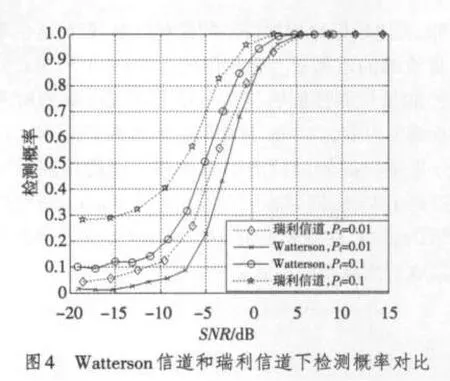
在该方案中要求天线数为奇数,每根天线上进行独自判决。采用“多数判决原则”将首次判决结果的数目K与参考值G(1≤G≤N)进行比较,如果K 仿真环境为Matlab7.1。 信道参数为:多普勒频移5 Hz,频扩5 Hz,多径为3,延时Delay=[0.003 s,0.005 s],信道为低通等效信道。 用户参数:第一用户信号是QPSK调制信号,其带宽为1 kHz,采样频率为10 kHz。 对几种能量检测方法在Watterson信道下进行仿真,并和瑞利信道下的能量检测性能进行了对比。 根据上面所分析的Watterson信道模型,从多径、衰落等方向进行仿真。系统总体框图[4]如图2所示,其中多径效应可以分别对原始输入信号进行延时得到,只需将预设的频移和频扩改变相应路径上的阶增益系数便可达到效果,这里设置为固定的5 Hz。 图3为单频信号经过多普勒频移和频扩后的频谱图,从频谱图中可以看出其频率发生了偏移和展宽,并且产生了多径效应,每条多径信号分别出现了多普勒频移和多普勒频扩现象。 对通过Watterson信道下的QPSK信号采用能量检测方法进行频谱感知,并和通过瑞利信道下的情况进行了对比,其中观察时间为10 ms。由图4可知信号通过Wat⁃terson信道和瑞利信道后能量检测的概率,可以看出在SNR大于2 dB时2种信道下的检测概率均大于0.9,而在低信噪时,由于存在信道衰落、阴影和噪声不确定性等影响,检测性能相对较差。Watterson信道由于存在多径效应引起的时间选择性衰落和频率选择性衰落,使能量检测性能低于瑞利信道。 针对Watterson信道的特点,分别对通过Watterson信道的QPSK信号,采用SLC和MA分集接收能量检测算法进行了仿真。由图5可以看出不论哪种分集方案,在同一虚警概率和信噪比下,其检测概率都要比单天线的高。由表1的数据看出,特别是在低信噪比的情况下,采用SLC分集接收的检测性能明显占优,在L=3,SNR=-5 dB的情况下采用SLC分集接收的检测性能要比采用MA分集接收的检测性能高出将近一倍,比单天线的高出两倍。这是由于采用了分集接收提供的功率增益可以在一定程度上改善因噪声不确定性造成的信号不可检测的现象,可以不同程度地克服多径和信道衰落的影响。而SLC和MA这两种算法相比,SLC能够提供较大的功率增益,仿真结果也证明了在短波信道的衰落和色散的影响下采用SLC分集接收算法感知性能明显优于MA分集接收。并且,随着天线条数的增加,采用SLC分集接收的能量检测性能不断提高。 图6和图7分别针对SLC分集接收这种能量检测算法在Watterson信道下的性能进行了研究,随着观察时间的增加,可以较好地增加信号的检测概率,但是这也增加了能量检测的运算量。在相同的观察时间下,SLC分集接收的能量检测性能明显高于单天线无分集的检测性能。在观察时间为10 ms且相同检测概率下,采用L=3的SLC分集接收的能量检测信号比单天线的检测信号的SNR提高了4 dB,同时也可以看出由于Watterson信道多径色散的影响,在观察时间小于5 ms时,不管是否采用分集接收检测概率都很低。 表1 分集接收检测概率对比 研究了在Watterson信道下感知无线电中能量检测的性能,针对能量检测在信道存在衰落、阴影和噪声不确定性等影响时,性能相对较差的缺点,提出采用多天线分集接收的方法,并和瑞利信道下的检测性能进行了对比。仿真结果证明,对于Watterson信道采用分集可以对抗信道的多径和衰落现象,在一定程度上提高了能量检测的性能,其中平方律合并方案(SLC)性能最优。文中对影响SLC接收的一些参数进行了仿真,也可以看出虽然在低信噪比下SLC分集接收的方法可以较好地改善其检测概率,但观察时间低于5 ms,即使采用分集也很难达到较好的检测性能。 [1] HAYKIN S.Cognitive radio:brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220. [2] CABRIC D,MISHRA S M,BRODERSEN R W.Implementation issues in spectrum sensing for cognitive radios[C]//Proc.38th Asilomar Conference on Signals,Systems and Computers 2004.[S.l.]:IEEE Press,2004:772-776. [3] VOGLER L E,HOFFMEYER J A.A model for wideband HF propagation channels[J].Radio Science,1993,28(6):1131-1142. [4] 李丁山,杨莘元,杨平.基于Watterson模型短波信道仿真算法[J].系统工程与电子技术,2004,26(11):1558-1560. [5] URKOWITZ H.Energy detection of unknown deterministic signals[J].Proceeding of IEEE,1967,55:523-531. [6] DIGHAM F F,ALOUINI M S,SIMON M K.On the energy detection of unknown signals over fading channels[J].IEEE Trans.Communications,2007,55(1):21-24. [7] HWANG S H,BAEK J H,DOBRE O A.Spectrum sensing using multiple antenna-aided energy detectors for cognitive radio[C]//Proc.IEEE Conference on Electrical and Computer Engineering.[S.l.]:IEEE Press,2009:209-211.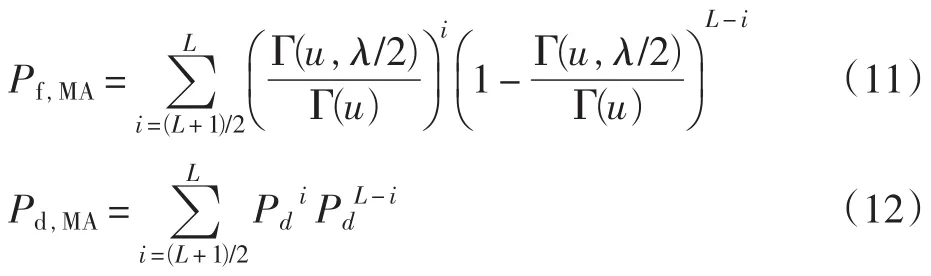
3 Matlab仿真及性能分析
3.1 Watterson信道仿真
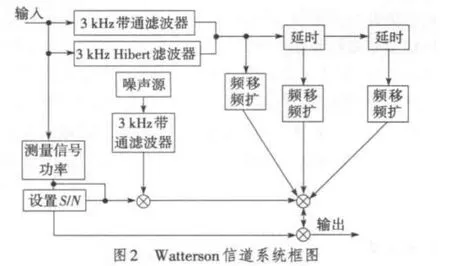
3.2 Watterson信道下能量检测仿真
4 小结
