简单中的丰富——例谈组合问题

●虞金龙 (绍兴市第一中学 浙江绍兴 312000)

简单中的丰富
——例谈组合问题

●虞金龙 (绍兴市第一中学 浙江绍兴 312000)

组合数学历史悠久．早在几千年前，我国的《河图》、《洛书》中就已经涉及一些简单有趣的组合问题了．组合问题看似简单，这个在小学数学就出现的知识点一直在各级竞赛中占有一席之地．组合问题中丰富的内涵，又经常令广大数学爱好者折服．组合问题在开阔学生思路、培养灵活思维习惯方面起着重要作用．

本文例举讨论组合问题中的几个常见模型，旨在抛砖引玉．

1 组合中的极值问题

例1平面上给定 n个点 A1，A2，…，An(n≥3)，任意3个点不共线．由其中的k个点对确定的k条直线(即过k个点对中的每一点对作一条直线)，使得这k条直线不相交成3个顶点都是给定点的三角形．求k的最大值．

分析设过点对A1，A2的直线为l，则点A1，A2不能同时与其余n－2个点中的任意一点连接，即过点A1或A2的直线至多只有n－1条(包括l)．同理，对 A3，A4，…，An这 n －2 个点而言，过 A3或 A4的直线至多只有n－3条，所以

例2将1到n2这n2个自然数随机地排列在n×n的正方形方格内，其中n≥2．对于在同一行或同一列中的任一对数，计算较大数与较小数之比．这n2(n－1)个比值分数中的最小值，称为这种随机排列的“特征值”，求“特征值”的最大值．

其中a，b分别是这一行或这一列中的最大数，且a＞b．如果所有这n个大数在不同的行与列中，那么当它们中的一个数与n2－n在同一行或同一列中时，有

其中a为与n2－n在同一行和同一列中的2个最大数中的较小的一个．对于排列

在第 j=2，3，…，n －1 列，从小到大排列为:j－1，j－2+n，j－3+2n，…，1+(j－2)n，n+(j－1)n，…，j+(n－1)n．其中前j－1项为公差为 d=n－1的等差数列，后n－j+1项仍为公差为d=n－1的等差数列，第j项与第j－1项的差为2n－1，于是

当j=n－1时，最后一个等号成立．

在第n列，当n≥3时，

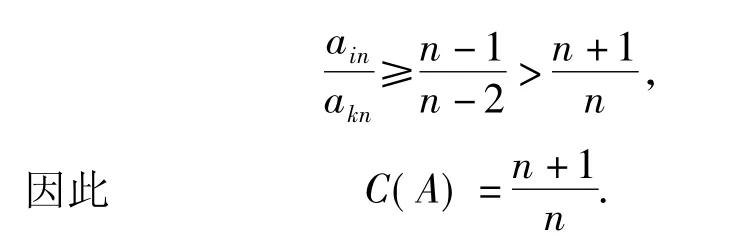
例3在7×7个方格的正方形中，作出其中m个正方形的中心，使这m个点中的任意4个点都不能构成边与网线平行的矩形，求m的最大值．

分析假设在7×7个方格的正方形中，已作出m个正方形的中心点且满足题目要求，其中第i行有xi个中心点，则

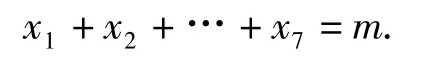
按已知，如果在某行已作出2个点，那么在其余的每行中都不能再标出具有相同横坐标的2个点，这意味着正方形中所有的同行两点组的横坐标对互不相同．由于方格的横坐标有7个不同的值，因此不同的横坐标对共有=21个，从而

图1

即至多可作出21个方格的中心满足条件．

当m=21时，构造如图1所示的排列方法可以满足条件，故m的最大值为21．

2 组合中的构造问题

例4能否将正整数集合N*分划为2个不相交的集合A和B，使得

(1)A中任意3个数不成等差数列;

(2)不能有B中的元素组成一个非常数的无穷等差数列．

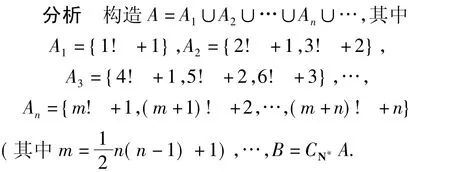
将A中的数从小到大排列，从第2项起，每一项大于前一项的2倍，因此A中任意3个数不成等差数列，其次B中没有非常数的无穷等差数列．

假设有{a+nd}(n=0，1，2，…)是 B 中一个非常数的等差数列，这里 a，d∈N*．由A的构造可知，存在无穷多个m∈N*，使得m!+a∈A，故存在m≥d，使得 m!+a∈A．令 n=，则 m!+0a=a+n0d∈A，这与对任意 n∈N*，a+nd∈B 矛盾．

可见，存在满足条件(1)，(2)的集合A，B．

例5设k为给定的正整数，试求最小正整数n，使得对任意n个整数，其中总存在2个整数，它们的和或差被2k整除．

分析设a1，a2，…，an为任意 n个整数，它们被 2k 除的余数依次为 r1，r2，…，rn，于是 ri∈{0，1，2，…，2k－1}，将 2k 个数的集合{0，1，2，…，2k －1}分为下列两数和能被2k整除(只有一个数的组，同数相加或相减)的k+1组:

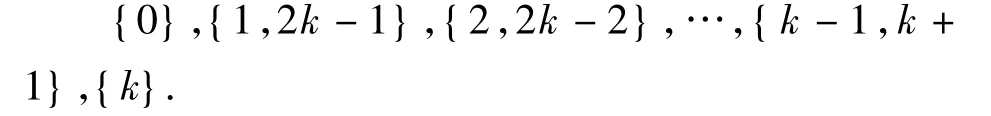
于是当n≥k+2时，根据抽屉原理，n个整数r1，r2，…，rn中必有 2 个数 ri，rj(1≤i＜j≤n)属于同一组，它们之和或差被2k整除，从而ai与aj的和或差被2k整除，故所求的最小正整数n≤k+2．

另一方面，取下列 k+1 个整数:0，1，2，…，k，它们中任意2个数之和在1与2k－1之间，任意2个数之差在－k与k之间并且不为0，这些和与差不能被2k整除，因此最小的正整数n≥k+2．

综上得所求的最小正整数n=k+2．

3 组合中的覆盖问题

例6在100×100的方格棋盘上放置着800个T形块，每个这样的图形恰好盖住棋盘上的4个方格，且任何2个图形都不重叠，求证:在棋盘上还可以再放置1个这样的图形，使它完全盖住4个空方格．

图2

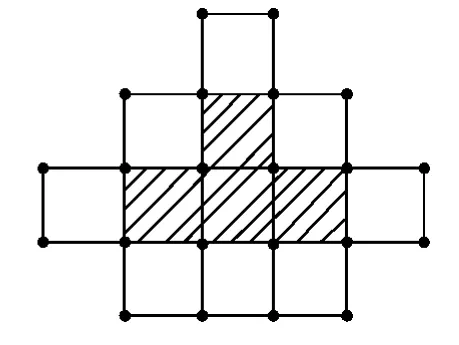
图3

分析将图2中阴影方格称为中心方格，假设在棋盘上已经放好1个T图形，这个T图形与其周围的8个方格如图3所示．如果棋盘上再放置一个T图形，且其中心格不在图3所示的12个方格中，则后放入的T图形与原来的T图形不相互重叠．另一方面，若放入的T图形的中心格不在棋盘四周的边格中，则此图形不会超出棋盘之外．由于棋盘内部共有98×98个方格，而982－12×800=4，故知还可以再放入1个T形图，使得它与已有的T图形不相互重叠．

例7能否用如图4所示的9块“田字型”方块和7块“L型”的模块把国际象棋盘覆盖?

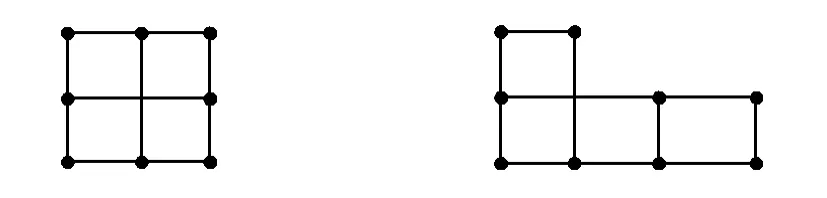
图4

分析国际象棋盘是8×8的64个方格，将奇数列的每一个小方格内赋值1，偶数列的每一小方格内赋值－1，于是每块田字形块盖住的方格内的数字之总和为0;而L形模块盖住的方格内的数字之和为3+(－1)=2或1+3×(－1)= －2，设L形中的x块盖住数字和为2，7－x块盖住的数字之和为－2．如果满足题目条件的覆盖存在，那么盖住的各小格内的数字总和应为

另一方面，8×8的棋盘上各小格内的数字之和应为32×1+32×(－1)=0，因此4x－14=0，得 x=∉Z，矛盾．故满足题设的覆盖是不存在的．

4 组合中的计数问题

例8设 n≥2，S={1，2，…，n}，对于每个 1≤k≤n，记xk是S的所有k元子集合的最小元素的和，试求

因此，只要考虑n作为最小元素在和中的贡献．显然以n为最小元的集合只有一元集合{n}，从而n在所求和中的贡献为n，故所求的值是n．

例9某次经贸洽谈会共有12m(m∈N*)个单位参加，其中每个单位都恰好同其余3m+6个单位签过合同．对任何2个单位，同这2个单位签过合同的单位数是相同的．问共有多少个单位参加这次经贸洽谈会?

1 2 3 4 5 6 6 1 2 3 4 5 5 6 1 2 3 4 4 5 6 1 2 3 3 4 5 6 1 2 2 3 4 5 6 1

用1，2，3，4，5，6 表示 6 种颜色，将单位染色，按上表排列，每单位恰好与它同行或同列或与它具有相同颜色的单位签约，这样保证每个单位恰与15个单位签约，只需再证这种构造满足第2个条件即可．设P，Q是任意2个单位，若他们坐在同一行，则与这2单位签约的单位有这一行的其余4个单位及位于P所在列与Q同色的单位和位于Q所在列与P同色的单位，则2个单位共同签约的6个单位分别是:位于P所在的行和Q所在的列的1个单位(与P，Q均不同色)、位于P所在列和Q所在的行的1个单位、位于P所在行和列且与Q同色的2个单位、位于Q所在行和列且与P同色的2个单位．

5 组合中的操作问题

例10任意地将数1，2，…，n写在一个圆周上．允许每一次交换相邻的位置，只要这2个数之差的绝对值大于1，试证经过若干次这样的交换之后，可以使得所有数按自然顺序排列在圆周上．

分析规定顺时针方向为正向．首先，可以交换1与其他数的位置，使得1与2相邻且1排在前面，然后将2按顺时针方向交换并前进，直到与3相邻，接着再将1与其他数交换，使之与2相邻，从而得到1，2，3按顺时针方向排好，再用3倍的交换步骤，依次使3与4，2与3，1与2靠拢，于是1，2，3，4已经排好．这样继续下去，最后便可使全部各数都按正方向排好，显然，反方向排列同样也可以操作成功．

例11国际象棋盘有32个黑格与32个白格，每次操作把位于内部的2×2正方形的每个方格改变成另外的颜色，问能否通过若干次操作使得棋盘里恰好剩下一个白色的方格?

分析8×8国际象棋盘中有32个黑格与32个白格，规定给每个黑色的格子赋值1，给每个白色的格子赋值－1，初始状态有32个1和32个－1，它们的乘积为

每次操作改变2×2=4个方格的颜色，相当于把4个方格的数值改变符号，对于64个格子的数值乘积S而言，每次操作相当于乘以(－1)4．如果先后共进行了k次操作，k次操作后格子中数值的乘积为不可能为163×(－1)，因此无论通过多少次操作不可能使得棋盘里恰好剩下一个白色的方格．

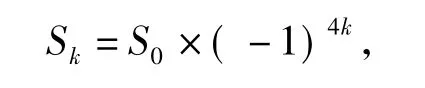
例12在黑板上写上3个整数，然后将其中一个擦去，换上其他2个数之和与1的差．将这个过程重复若干次之后得到(17，1 999，2 015)，则这3个数的初始值能否是

(1)(2，2，2);

(2)(3，3，3)．

分析由于3个数在题述的操作过程中奇偶性的变化关系为(偶，偶，偶)→(偶，偶，奇)→(偶，偶，奇)，因此(2，2，2)无法经过若干次操作达到(17，1 999，2 015)．

若(奇，奇，奇)→(奇，奇，奇)→(奇，奇，奇)，则(3，3，3)有可能是操作过程的初始值．

若先考虑(3，3，3)经过若干次变化后达到(17，a，b)(17 ＜a ＜b)，则

显然2 015=1 999+16也满足．

固定17，选择尽可能小的 a＞17，使得(17，a，a+16)经过若干次调整操作能达到(17，1 999，2 015)．对(17，a，a+16)，若擦去 a+16，则操作后仍为自己不动，故应考虑擦去a，此时经操作后得(17，a+16，a+2 ×16)．再擦去 a+16，经操作后得

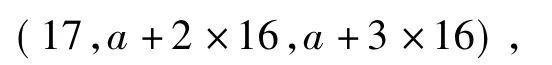
经过n次操作可得

由于1 999=31+123×16，因此若取 a=31，则(17，31，47)需要123次擦去中间数的操作可达(17，1 999，2 015)．

又因为由递推:(17，31，47)←(15，17，31)←(3，15，17)←(3，13，15)←(3，11，13)←(3，9，11)←(3，7，9)←(3，5，7)←(3，3，5)←(3，3，3)，知(17，31，47)可由(3，3，3)经过 9 次操作达到，所以(17，1 999，2 015)可由(3，3，3)经过 123+9=132次操作达到．

数学竞赛中出现的组合问题，其表达形式往往简单、明了，而求解它们却需要敏锐的观察力、丰富的想象力和必要的技巧，通常没有一定的模式可循，而且各种难易程度的问题都非常丰富．因此各种程度的智力训练和数学竞赛中，大多离不开组合问题．