支持向量机优化的克里金插值算法及其海洋资料对比试验

0 引言

由于观测仪器、手段和观测环境的限制，在时空上均匀分布的连续观测数据通常很难获得，不足以满足科学研究的需要，因此需要对现有的不规则数据进行插值以提供均匀的网格化资料(Liu et al.，1998;Wang et al.，2008)。常用插值方法主要包括逐步订正法、最优插值法、样条函数插值法、分形插值法、克里金插值法等(Cressman，1959;McIntosh，1990;Oliver and Webster，1990;杨晓霞等，1991;潘晓滨等，1996;李培军等，2005;刘巍等，2010)。

克里金插值(Kriging interpolation)是基于地质统计学变异函数模型而发展起来的空间插值方法，是一种最优的无偏、线性估计方法。克里金法正在被广泛地应用于地质学、水文学、土壤科学、气象、农业、遥感、石油工程、生态、海洋、资源与环境以及其他研究“时空变量”的领域(常文渊和戴新刚，2004;张仁铎，2005;李伟等，2007;甄计国等，2009)。

在克里金插值中，十分关键的问题是选择反映数据分布空间结构特征的变异函数，其决定着空间插值的精度(张仁铎，2005)。常见的变异函数模型有:线性模型、球形模型、指数模型、高斯模型等。一般情况下，变异函数模型的选取是，根据样本的变异结构云图(又称实验变异函数，experimental variogram)来选取最接近其结构特征分布的内置变异函数。这种传统的变异函数选取方法具有较大的主观性，利用不同的变异函数模型得到的克里金插值效果差别较大，且不一定能选取最优的变异函数模型。

为此，本文针对常规克里金插值方法变异函数固定内置不利于针对性地刻画实际数据结构分布的缺点，提出用最小二乘支持向量机方法从实际资料场中拟合重构变异函数，进而对常规克里金插值方法进行变异函数优化的研究思想和算法途径，即支持向量机—克里金法(SVM-Kriging)。该方法可根据不同的资料场结构特征分布进行变异函数的自适应拟合，进而克服常规方法中变异函数选择的主观性，提高了插值精度。

1 常规克里金法

1.1 基本原理

这里对克里金插值法的基本原理作简要介绍，关于克里金法基本原理和变异函数更详细内容请参见张仁铎(2005)。

设Z表示某一变量的数值大小，x表示空间位置点，Z(x)表示点x处变量Z的值。

设普通克里金法的估计公式为:

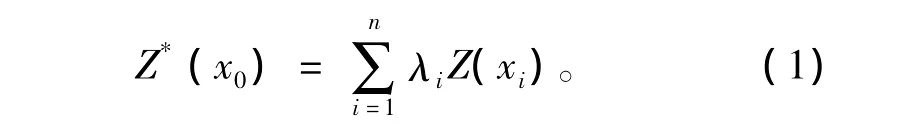
其中:Z(xi)是xi位置的测量值;λi为待定系数，表示分配给Z(xi)的残差的权重;Z*(x0)是在x0位置的估计值;n是用于估计过程的测量值的个数。

为了保证无偏估值，令E［Z*－Z］=0(E表示数学期望)，则有

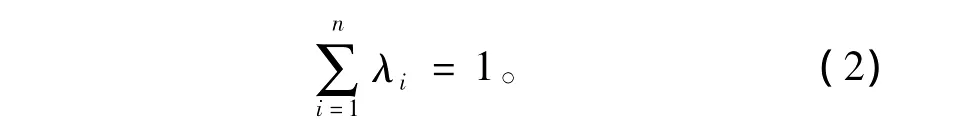
根据这一条件，估计误差的方差表达式可以简化为

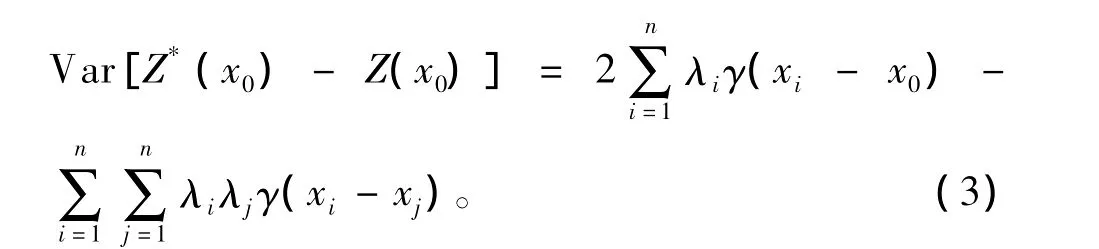
式中:Var表示方差;γ(h)是变异函数。在限制条件(2)下，为使(3)式的估计方差最小，引入拉格朗日乘数μ，通过推导得出计算权重的克里金线性方程组

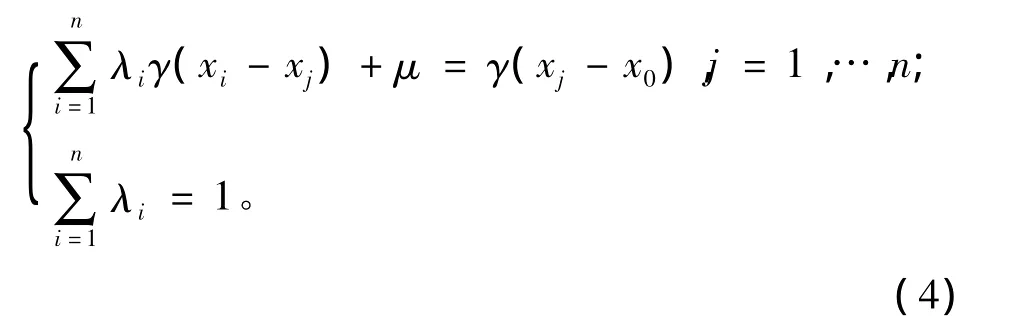
式中γ(xi－xj)表示距离为xi和xj之间的变异函数值。解方程(4)即可得到所有权重λ1，…，λn和拉格朗日乘数μ，于是利用估计公式(1)就可以得到估计值Z*。

1.2 变异函数

克里金插值的核心是根据样本点来确定研究对象(某一变量)随空间位置而变化的规律，以此去推算未知点的属性值。这个规律，就是变异函数。变异函数是用来描述区域化变量结构性和随机性这一空间特征而提出的。

样本的变异函数(即实验变异函数)可以通过下式进行计算:

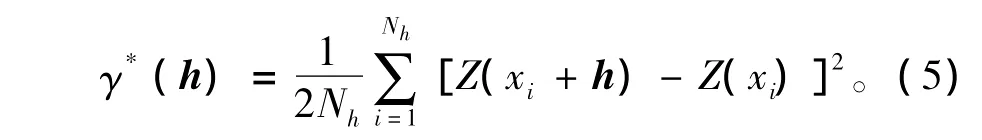
其中Nh为距离相隔为矢量h的所有点对的个数，矢量h叫做分离距离。如果γ(h)=γ(r)，r=|h|=h(h的数值大小)，即γ只依赖于分离距离的大小而不依赖于它的方向，则称γ为各向同性的，也称变量Z是各向同性的。为简单起见，以下考虑普通克里金法的各向同性情况。

变异函数核心思想是把所有的点对按照间隔距离的大小进行分组，在每一个组内，计算每个点对变量值的差异，最后取平均作为该组变量值的差异(变异值)。这样，将整个空间分为不同大小的组，并有相对应的属性差值。根据样本点计算某一未知点的属性值时，会考虑到多种不同距离空间点位的相关关系。

一般情况下，利用采样点及变异函数的计算公式(5)得出样本点的实验变异函数，观察其分布图像，寻找合理的变异函数模型，按照估计方差最小的原则，运用最小二乘法进行拟合，拟合后的曲线为经验变异函数。变异函数模型是克立金空间插值的前提条件，同时它也决定着空间插值的精度。变异函数模型通常选为某一种理论模型。常见的理论模型有:线性模型、球形模型、指数模型、高斯模型等。数学表达式如下:

线性模型γ(h)=C0+C1h;

球形模型γ(h)=

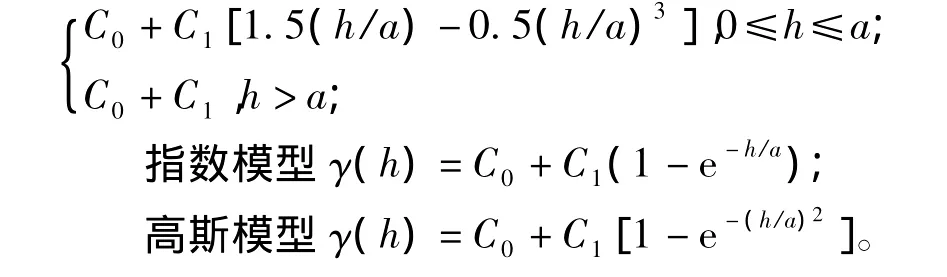
其中，C0，C1，a为待定参数。变异函数的选取，不仅仅是将实验的点变异函数拟合为经验的模型变异函数曲线问题，用户需要根据自己的经验去选择基本变异函数模型的类型，而这种选取方法通常带有一定的主观性和随意性。

1.3 存在问题

目前，在常规克里金插值方法中对变异函数模型的选择还没有很好的方法，往往要通过选择不同的变异函数模型进行插值效果比较后确定，这种常规做法比较耗时(需要进行多次克里金插值计算)，且变异函数模型类型比较有限，难以从中找到适合实际数据场分布特征的变异函数模型，因此，常规方法带有很大的主观性和随意性。针对克里金法中的变异函数模型选取方面存在的问题，本文采用最小二乘支持向量机对实验变异函数进行拟合，可以避免变异函数模型类型选择方面的不足。它不需要根据自己的经验去选择基本变异函数模型类型的问题，而是直接根据实验变异函数云图分布来进行拟合。下面介绍最小二乘支持向量机。

2 最小二乘支持向量机

支持向量机(SVM)由Vapnik(1995)提出，是近年来出现的基于统计学习理论的解决多维函数拟合和预测问题的机器学习工具。其主要思想是:通过事先选择的非线性映射将输入向量映射到高维特征空间，在这个空间中构造最优决策函数。在构造最优决策函数时，它利用了结构风险最小化原则，同时还巧妙利用了原空间的核函数取代了高维特征空间的点积运算。Suykens et al.(2001)提出的最小二乘支持向量机(LS-SVM)是支持向量机的一种，它是将标准支持向量机算法中的不等式约束转化为等式约束而得到的。其主要思想如下。

对非线性回归问题，设训练样本为(x1，y1)，…，(xl，yl)∈Rn×R。非线性回归函数为

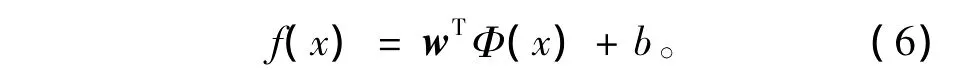
对于最小二乘支持向量机，优化问题变为

其中C为正则化参数。求解式(7)的优化问题，可以引入Lagrange函数

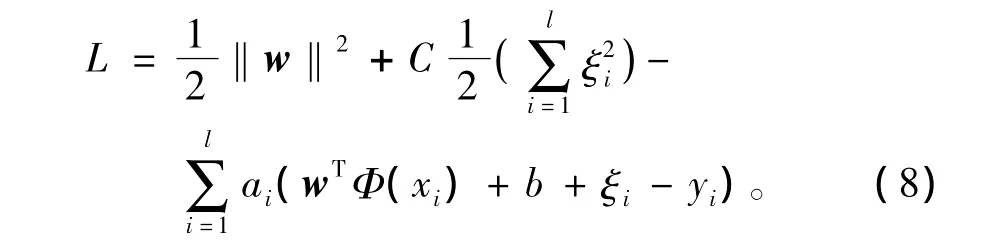
式中:ai为Lagrange乘子;常数γ＞0，它控制对超出误差的样本的惩罚程度。最优的ai和b可以根据KKT(Karush-Kuhn-Tuchker)条件，转化为求解如下的线性方程

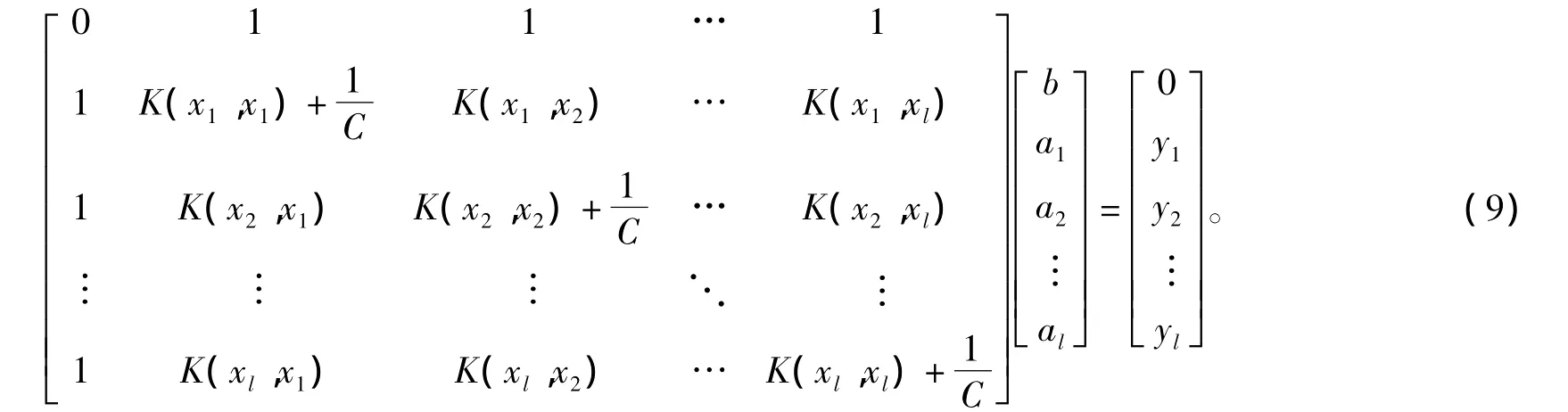
其中:K(xi，xj)为核函数。

从而得到非线性回归函数的解为

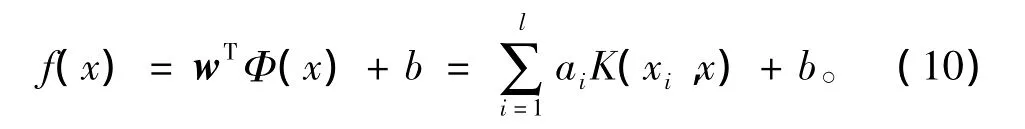
最常用的核函数有以下几种:多项式核函数K(xi，xj)=(σ(xi·xj)+r)d，σ＞0;Sigmod核函数K(xi，xj)=tanh(σ(xi·xj)+r);RBF核函数K(xi，xj)=exp(－σ‖xi－xj‖2)，σ＞0。

刘科峰等(2006)研究表明，RBF核函数效果相对较好。因此，文中最小二乘支持向量机的核函数选用RBF核函数。核函数确定后，还需确定两个相关的参数:σ、C。其中σ为核参数，调节核函数的平滑程度;C控制模型误差的大小。这两个模型参数在很大程度上决定了该模型的学习能力及泛化能力，本文采用刘科峰等(2006，2009)提出的遗传算法对参数进行优化选择。

3 支持向量机—克里金(SVM-Kriging)方法

常规克里金方法中常采用观察实验变异函数图分布特征，寻找合理的变异函数模型。本文针对克里金法中的变异函数模型选取方面存在的问题，提出了采用最小二乘支持向量机对实验变异函数进行拟合的方法，能够对实际数据场分布的结构特征进行自适应判别，从而有效地克服了常规方法的主观性和随意性。

支持向量机—克里金方法可分为以下3个主要步骤:

1)通过公式(5)计算样本的实验变异函数γ*(h)，得到γ*(h)随分离距离h的变化规律;

2)采用第2节提出的经过遗传优化参数的最小二乘支持向量机法对实验变异函数γ*(h)进行拟合，得到经验变异函数γ(h);

3)对于各待估点x0，利用公式(4)可解出其对应的权重λ1，…，λn，然后代入公式(1)可得到变量在x0处的估计值Z*(x0)。

4 海洋资料对比试验

海洋观测资料对于研究海洋环境特征及其演变都具有极为重要的影响和作用，但是由于观测手段和研究成本的制约，观测资料不足，已有资料大多稀疏，不能很好地满足海洋研究的需要，因此，对既有的数据资料进行加密插值是挖掘和拓展数据信息资源的重要途径。

为了检验利用最小二乘支持向量机拟合变异函数的克里金插值效果，本文利用GODAS(global ocean data assimilation system)资料进行应用实验。GODAS资料是NCEP的一种月平均全球资料同化系统资料。选用资料范围为［120.5°E～71.5°W，60°S～58°N］，要素包括海表盐度(本文为5 m深处盐度)和海面动力高度(SSH)。为代表性起见，资料时间分别为2006年1月、4月、7月、10月，可以基本代表冬、春、夏、秋4个季节。

4.1 插值算法流程

因各要素、各月份的克里金插值方法类似，故本文以2006年1月海面动力高度场为例进行算法应用试验说明。

选择［120.5°E～71.5°W，60°S～58°N］范围内海面高度场网格点数据，网格精度为2°×2°，共有85×60=5 100个网格点，其中在海洋上共有4 215个网格点，陆地上网格点变量值无意义。从4 215个网格点中随机抽取出75%的网格点资料(共3 161个)作为交叉验证数据，利用余下的25%网格点资料(共1 054个)作为已知信息进行数据的插值恢复试验。图1为余下的25%数据场(插值信息场)。

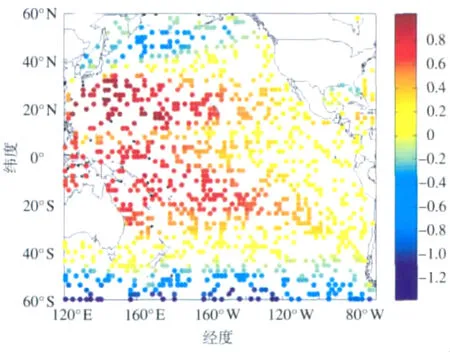
图1 抽取75%格点数据后余下用于插值试验的散点海表动力高度场(单位:m)Fig.1 Remaining sea surface height data for interpolation test after take out of 75%of available data(units:m)

首先，对数据进行预处理。将经纬度坐标(θi，φi)(i=1，…，n)进行如下变换:

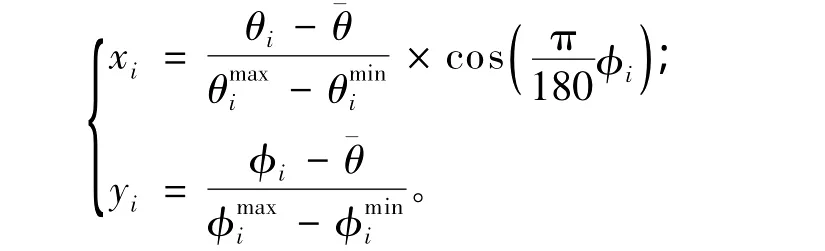
其次，计算实验变异函数。利用已知的1 054个信息，按照公式(7)计算得到实验变异函数(图2)。

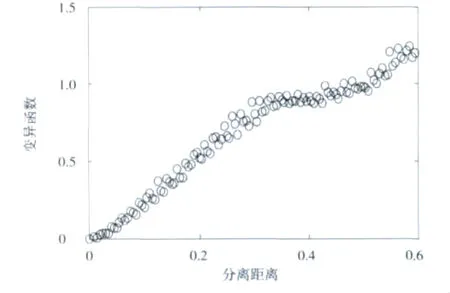
图2 实验变异函数Fig.2 Experimental variogram

第三，得到经验变异函数。分别采用4种常规的变异函数模型和本文提出的支持向量机模型进行实验变异函数的拟合，得到经验变异函数(empirical variogram)，如图3所示。同时，可算出曲线拟合相关系数分别为支持向量机0.988 4、高斯函数0.983 3、指数函数0.988 2、线性函数0.970 4和球形函数0.986 6。这5种变异函数模型中以支持向量机拟合的相关系数最高。

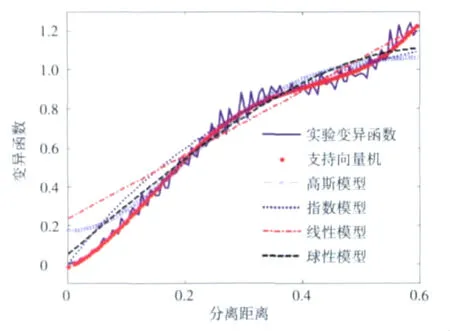
图3 不同变异模型函数拟合曲线Fig.3 Experimental variogram and fitting curves of different models

最后，得到各待估点处变量值。利用拟合得到的不同经验变异函数分别对各个待估点进行普通克里金插值，得到插值恢复场。

其他月份和变量的插值过程类似，此处略去描述。

4.2 交叉验证结果

本文采用交叉验证的方法对插值结果进行了分析对比。交叉验证法即首先预留一个或多个数据样点，然后用其他样点数据来估计该点以检验插值精度，评价某一指定的插值方法的质量。本文随机选取75%资料作为交叉验证数据。误差结果定量化指标为:平均误差Em，平均绝对误差Ema，均方根预测误差Ermsp。Em总体反映估计误差的大小，Ema可以估量估计值可能的误差范围，Ermsp可以用来比较不同的插值方法，其值越小，插值方法越好。设交叉验证的数据个数为n，则Em、Ema、Ermsp的定义如下:

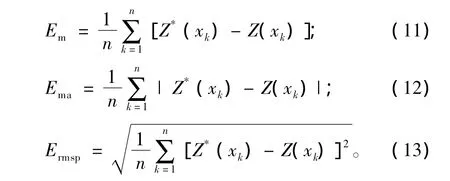
分别采用高斯函数、指数函数、线性函数、球形函数和支持向量机模型拟合变异函数，对2006年1月、4月、7月、10月的海表盐度和海面动力高度进行普通克里金插值。表1、表2是交叉验证法检验得到的各月误差结果及各要素4个月的平均误差结果。

由表1、表2可以看出:总的来说，支持向量机—克里金法插值产生的均方根预测误差相比其他常规克里金法(包括高斯函数模型、指数函数模型、线性函数模型、球形函数模型)均较小，支持向量机—克里金法对于不同变量、不同时间的实际数据场具有较大的自适应优势。

5 小结

克里金插值结果对变异函数的选择依赖性较大，不同的变异函数导致不同的插值效果。选择合适的方法拟合变异函数对于改进克里金插值效果具有较大作用。本文以海表盐度、海表动力高度等海洋资料为例进行插值比较研究。对于不同时间的资料，各插值方法效果的优劣会有一定差别，故方法普适性还待更多资料的插值试验验证。总的来说，本文提出的基于支持向量机拟合变异函数的克里金插值相比其他几种模型函数(高斯函数、指数函数、线性函数、球形函数)具有较大的优势。事实表明，基于支持向量机拟合的变异函数对克里金插值结果有较大改进，它可以避免变异函数模型选择的主观人为性，因此适用于实际要素场资料(特别是数据结构复杂和分布特性先验未知)的客观分析与自动插值处理。

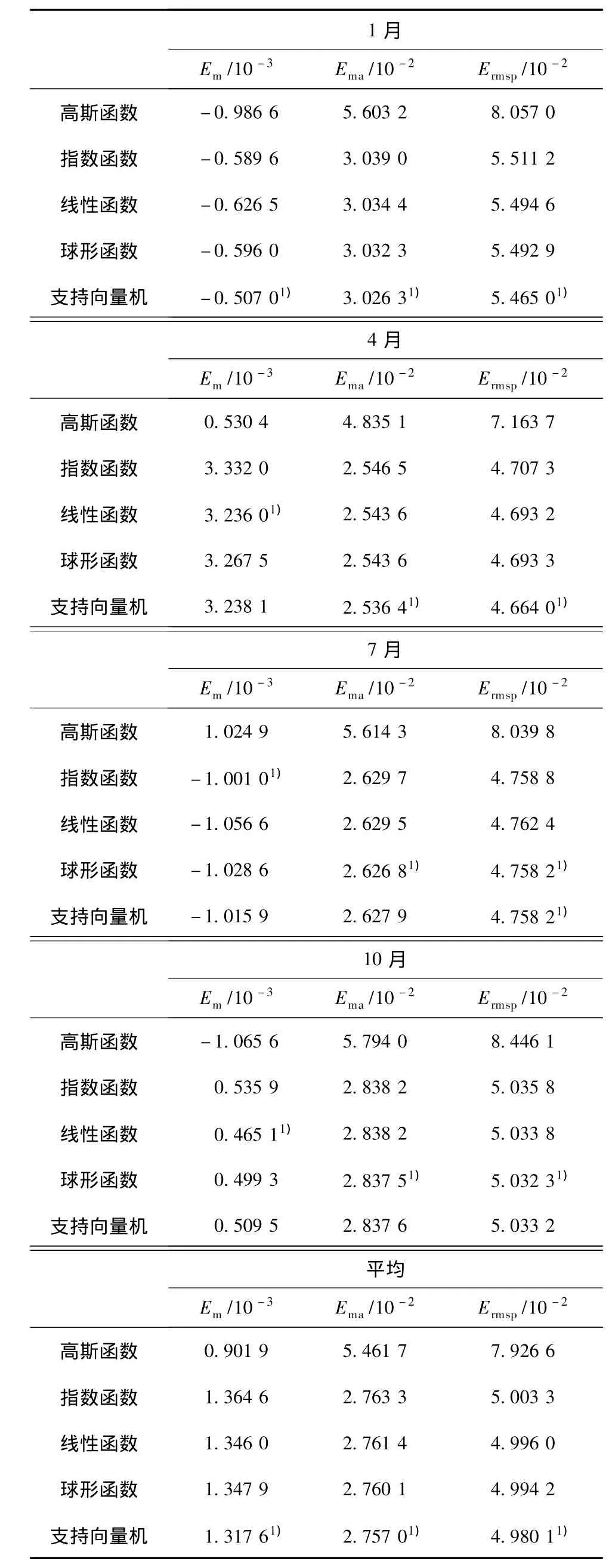
表1 海面动力高度的各种不同插值变异模型结果比较Table 1Interpolated quality comparison of sea surface height based on different variogram modelsm

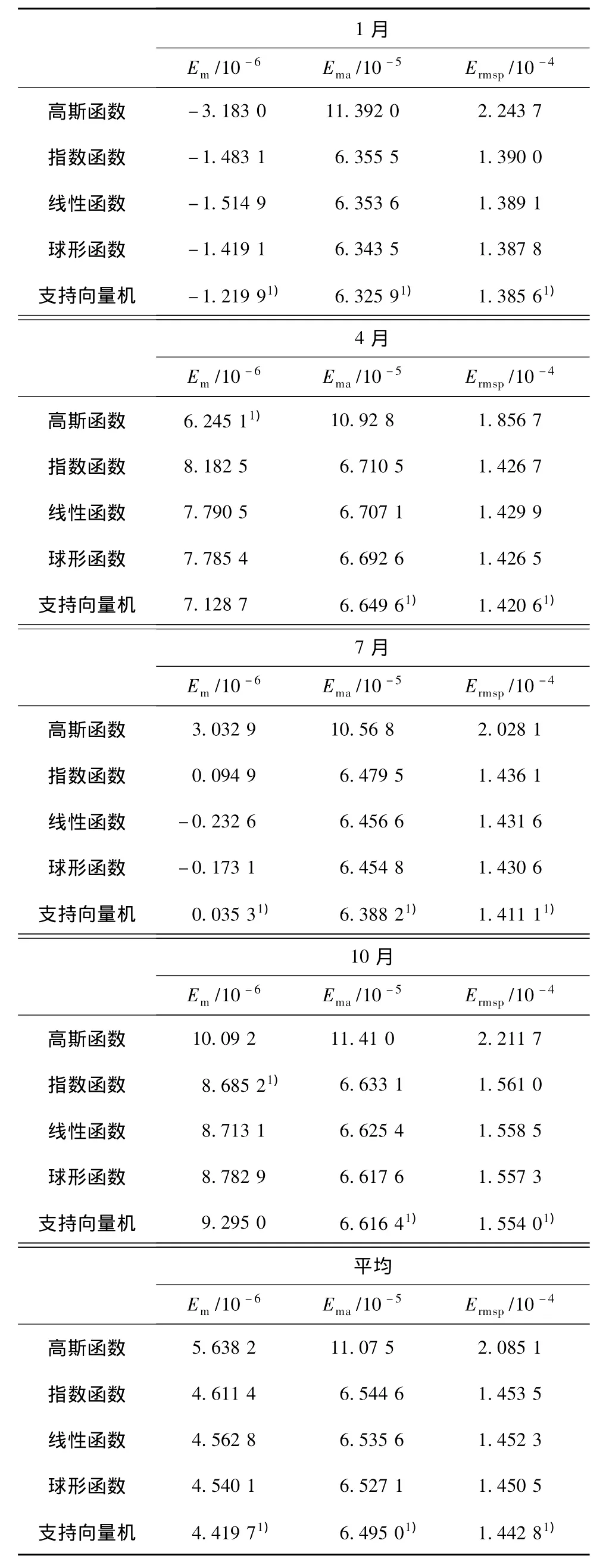
表2 海表盐度的各种不同插值变异模型结果比较Table 2Interpolated quality comparison of sea surface salinity based on different variogram modelsPSU

常文渊，戴新刚.2004.地质统计学在气象要素场插值的实例研究［J］.地球物理学报，47(6):40-47.

李培军，张维峰，郭洪涛，等.2005.气象资料三维化技术中的插值问题［J］.气象科学，25(6):617-623.

李伟，李庆样，江志红.2007.用Kriging方法对中国历史气温数据插值可行性讨论［J］.南京气象学院学报，30(2):246-252.

刘科峰，张韧，万齐林，等.2006.结构风险极小的支持向量机方法及其在副热带高压数值预报优化中的应用［J］.应用基础与工程科学学报，14(增刊):384-390.

刘科峰，张韧，洪梅，等.2009.基于最小二乘支持向量机的副热带高压预测模型［J］.应用气象学报，20(3):354-359.

刘巍，张韧，王辉赞，等.2010.分形插值参数的遗传优化及其ARGO海温场应用试验［J］.大气科学学报，33(2):186-192.

潘晓滨，魏绍远，马华平，等.1996.逐次最优插值方案及其试验［J］.气象科学，16(1):30-39.

杨晓霞，沈桐立，徐文金，等.1991.最优插值客观分析方法［J］.南京气象学院学报，14(4):566-574.

张仁铎.2005.空间变异理论及应［M］.北京:科学出版社.

甄计国，陈全功，韩涛.2009.甘肃省各流域降水量的GIS模块插值估计与改进［J］.气象科学，29(4):467-474.

Cressman G P.1959.An operational objective analysis system［J］.Mon Wea Rev，87:367-374.

Liu W T，Tang W，Polito P S.1998.NASA scatterometer provides global ocean-surface wind fields with more structures than numerical weather prediction［J］.Geophys Res Lett，25(6):761-764.

McIntosh P C.1990.Oceanographic data interpolation:Objective analysis and splines［J］.J Geophys Res，95(C8):13529-13541.

Oliver M A，Webster R.1990.Kriging:A method of interpolation for geographical in formation system［J］.Int J Geographical Information Systems，4(3):313-332.

Suykens J A K，Vandewalle J，Moor B D.2001.Optimal control by least squares support vector machine［J］.Neural Networks，14:23-35.

Vapnik V N.1995.The nature of statistical learning theory［M］.New York:Springer Verlag.

Wang H，Zhang R，Liu W，et al.2008.Improved interpolation method based on singular spectrum analysis iteration and its application in missing data recovery［J］.Appl Math Mech，29(10):1351-1361.