遗传算法求解最大预报误差的可行性研究

郑琴，张露，戴毅，陆小庆

(解放军理工大学理学院，江苏南京211101)

0 引言

数值天气预报与人们的日常生活息息相关，一些灾害性天气(如台风、暴雨)给人民的财产和生命安全构成极大威胁，也对国家的经济发展产生一定影响，因此提高预报效果、减少预报误差，具有十分重要的意义。然而，大气系统是一个非线性系统，且具有混沌特征，使得各种模式的预报结果对初始场的微小误差非常敏感，由于观测误差(包括仪器误差、观测点在时间和空间上的不够密集引起的插值误差等)的存在，导致初始场具有不确定性，从而大气的实际运动状态不可能被完全精确地描述出来，因此研究初始场的不确定性对预报效果的影响有着重要的理论意义和实践意义。

按照导致预报误差的原因不同，数值天气预报问题可以划分为两类:第一类可预报性与初始误差有关，第二类可预报性与模式误差有关。根据实际需求，Mu et al.(2002)又将与第一类可预报性相关的问题划分为以下3个子问题:最大可预报时间下界问题、最大预报误差上界问题、最大允许初始误差和参数误差下界问题。为了有效求解这3个子问题，最近Duan and Luo(2010)提出了一种新策略，由条件非线性最优扰动(conditional nonlinear optimal perturbation，CNOP)来实现这3个问题的求解。CNOP属带约束的优化问题，目前求解CNOP的主要方法是采用能处理约束条件的优化算法SQP(sequential quadratic programming)、SPG2(spectral projected gradient 2)(Mu et al.，2002;Mu and Duan，2003;Mu et al.，2003;Mu and Zhang，2006;Mu and Jiang，2007;Duan and Mu，2009;Duan and Luo，2010)和基于经验正交函数(empirical orthogonal function，EOF)分解的快速算法(Wang and Tan，2009)。SQP或SPG2是基于梯度信息的优化算法，其梯度由传统伴随方法(conventional adjoint method，ADJ)计算。许多CNOP的相关文献所采用的非线性模式均不含“开关”，因此传统伴随方法能为优化算法提供正确的梯度信息;然而，在数值天气预报中，对物理过程，特别是湿物理过程的参数化，会导致模式方程中的某些项关于时间或模式变量不连续或不可微，这种现象通常称为“on-off”开关问题(Xu，1996a，1996b;Xu and Gao，1999;Mu and Wang，2003;Mu and Zheng，2005;Wang et al.，2005;Zheng and Mu，2006;戴毅和郑琴，2007;郑琴和戴毅，2009)。当控制方程中有不连续“开关”时，目标函数相应它的某些初值的梯度不存在，传统伴随方法不能为优化过程提供正确的搜索方向，导致优化失败。基于EOF的快速求解CNOP方法，避免了伴随模式程序的编写和计算，该方法所求得的CNOP只是真正意义下的CNOP的一种近似，其近似程度与样本的选取密切相关，在实际应用中，可能会对误差增长的强度有所减弱(Wang and Tan，2009)。

为了避免上述各种方法的不足，寻求一种新的全局优化算法，求解CNOP和最大预报误差，显得尤为重要。遗传算法(genetic algorithm，GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索全局最优解的方法，整个迭代过程不需要梯度的相关信息。目前，遗传算法已被应用于资料同化(陈东升等，2004;胡娅敏等，2006;石娟等，2009;Fang et al.，2009)和CNOP的求解(Fang and Zheng，2009)等问题中。

本文以修改的Lorenz模型为预报模式，主要研究当模式含有开关时，遗传算法求解最大预报误差的可行性，有效克服了模式含有开关时，传统伴随方法不能为优化过程提供正确下降方向，以及经验正交分解方法只能求近似解的矛盾。第1节介绍CNOP和最大预报误差问题;第2节对修改的Lorenz模型进行简单描述，并分析其特点;第3节介绍遗传算法的基本原理和基本流程;第4节是数值试验，对于修改的Lorenz模型，分别选取模式的3个初始态，用传统伴随方法和遗传算法求解最大预报误差，比较分析试验结果，检验遗传算法求解该问题的可行性;第5节给出结论，并对遗传算法求解最大预报误差的优劣进行了简单的评述。

1 CNOP和最大预报误差

1.1 CNOP的定义

为了考察非线性对大气和海洋运动可预报性的影响，克服线性奇异向量和线性奇异值的缺点，Mu et al.(2003)提出了CNOP的概念，它是满足一定约束条件且在预报时刻有最大非线性发展的一类初始扰动。假设模拟大气和海洋运动的模式如下:

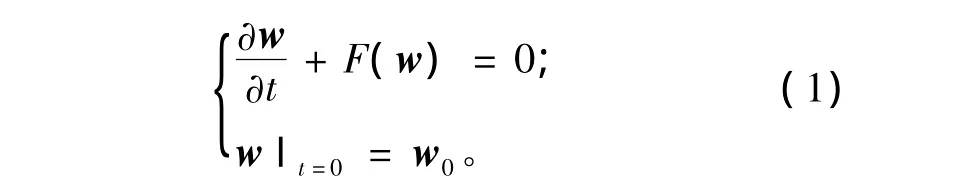
其中:w(x，t)=(w1(x，t)，w2(x，t)，…，wn(x，t));x=(x1，x2，…xn);t代表时间;F是非线性算子;w0是初始态。(x，t)∈Ω×［0，T］，Ω⊂Rn，T＜+∞。假设Mt是模式(1)从时刻0到t的传播算子，在初始态w0上叠加一初始扰动u0，在T时刻记初始扰动u0的非线性发展为u(T)，则

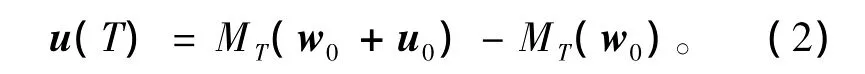
选取适当范数‖·‖，记目标函数为

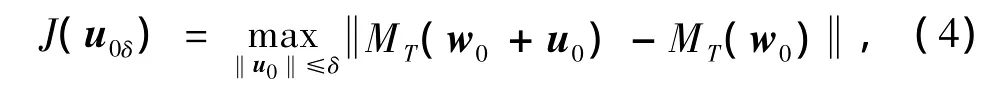
若初始扰动u0δ满足则初始扰动u0δ称为CNOP≤δ是初始扰动的约束条件。

目前，CNOP方法已广泛应用于资料同化(Fang et al.，2009)、目标观测(Tan et al.，2010)和可预报性问题(Mu et al.，2002;Mu and Duan，2003)的研究中。

1.2 最大预报误差上界问题

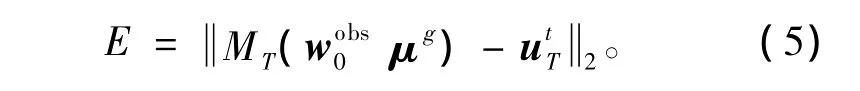
对于模式(1)，假设初始态的观测值wobs0和模式参数μg是已知的，在给定的预报时刻T，记预报误差为E，则为给定二范数是T时刻状态的真实值，然而这个真实值不可能确切知道，因此通过(5)式来求解预报误差E也是不可能的。为此，Mu et al.(2002)将此问题减弱为求解下列最大预报误差上界问题。若知道初始误差和模式参数误差的相关信息，如其中为给定范数，在(6)式成立的条件下，预报误差E可以通过下面的优化问题来估计，其中Bδ1和Bδ2分别是以和μg为球心、以δ1和δ2为半径的球。可证得E≤Ew，这样Ew就给出了预报误差E的上界估计。本文假定模式是完美的，不存在模式参数误差，只考虑初始观测误差。

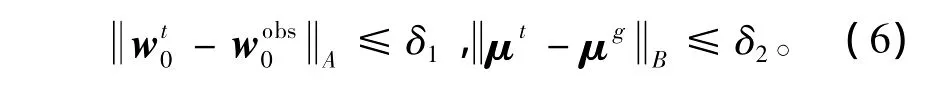
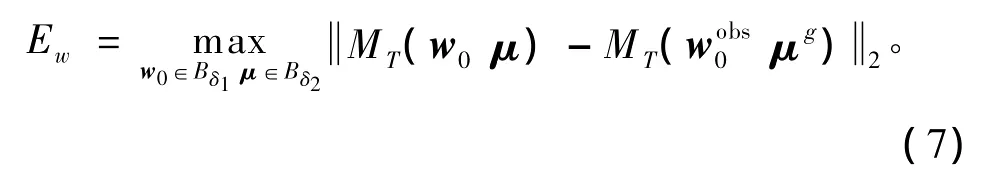
2 修改的Lorenz模型

美国著名气象学家E.N.Lorenz在研究大气环流模型的过程中，给出了用来刻画大气热对流不稳定性的Lorenz模型(Lorenz，1963):

其中r=r0+r1H(c)，c≡y－yc。令模式(9)中三个方程右端为0，可求出Lorenz模型的3个平衡点:

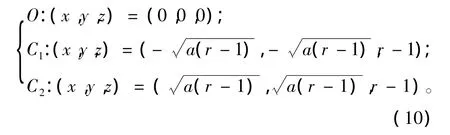
文中以该模型为理想模型进行数值试验，考虑到C1与C2两点的对称性，数值试验时取O点和C1点为模式初始态，为全面检验算法的有效性，另取一非平衡点A(－6.36，－8.27，21.2)共3个点为初始态，求解最大预报误差。

3 遗传算法

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，它从一组解出发，在迭代过程中利用遗传操作(选择、交叉、变异)来改善当前解，并用适应度函数来评判解的优劣，整个迭代过程不需要梯度信息。所以遗传算法提供了一种求解复杂系统问题的通用框架，它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，广泛应用于许多学科领域(陈东升等，2004;胡娅敏等，2006;朱玉祥等，2006;Fang et al.，2009;刘巍等，2010)。遗传算法的计算流程如下:

第1步确定决策变量和约束条件;

第2步建立优化模型，确定代价函数，即适应度函数;

第3步确定算法的相关参数，如种群大小、终止条件、选择概率、交叉概率、变异概率等;

第4步初始化种群;

第5步按照初始条件计算代价函数，选择种群中的最优个体，并判断是否满足终止条件?若满足，算法结束，输出最优解，若不满足，转到下一步;

第6步按照遗传策略，通过选择、交叉和变异算子产生新一代种群;

第7步判断种群中的个体是否满足终止条件?若满足，算法结束，输出最优解，若不满足，转到第6步。

遗传算法的寻优能力与遗传算子(选择、交叉和变异)的配置有很大关系，本文采用混合交叉和自适应变异算子。

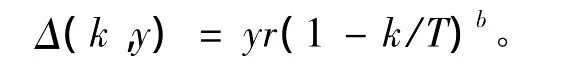
其中:r是［0，1］区间上的随机数;T是最大遗传代数;b是确定非均匀程度的参数，本文设定b=2。

求解CNOP属约束优化问题，将Deb(2000)提出的联赛选择和小生境技术用于遗传算法来求解最大预报时间上界。

4 数值试验

为了揭示开关对传统伴随方法的影响，检验遗传算法求解最大预报误差问题的可行性，在数值试验中以修改的Lorenz模型为理想模式，分别选取模式的3个初始态，用传统伴随方法和遗传算法来求解。传统伴随方法，首先写出模式的切线性方程和伴随方程，进而计算出梯度信息，给优化算法提供下降方向，求出CNOP和它所对应的预报误差即为最大预报误差的上界Ew;遗传算法，首先确定适应度函数以及一些相关参数，确定遗传操作方案，按第3节的计算流程搜索CNOP以及最大预报误差。

对于修改的Lorenz模型(9)，在数值试验时参数取值为:Prandtl数p=10，外形比a=8/3，r0=28，r1=－18，yc=－4.6，时间步长为0.005，取3个初始基态O点、C1点和A(－6.36，－8.27，21.2)点，最大初始观测误差δ取为0.08、0.8、1.6、2.4、3.2和4.0，分别取二范数()和无穷范数()进行试验。

4.1 初始基态为O点

对于修改的Lorenz模型(9)，以平衡点O点为初始态，预报时间步为300取为二范数，传统伴随方法和遗传算法的求解结果分别由表1和表2给出。

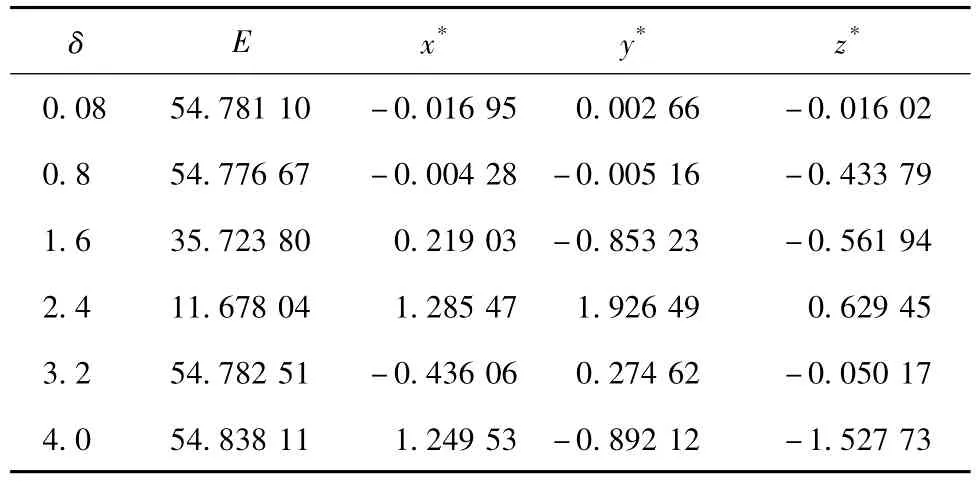
表1 初始态为O点、T=300、‖X‖2≤δ传统伴随方法求解结果Table 1Maximum prediction errors E and CNOPs yielded by the conventional adjoint method for the modified Lorenz model with the initial basic state O，T=300，and‖X‖2≤δ

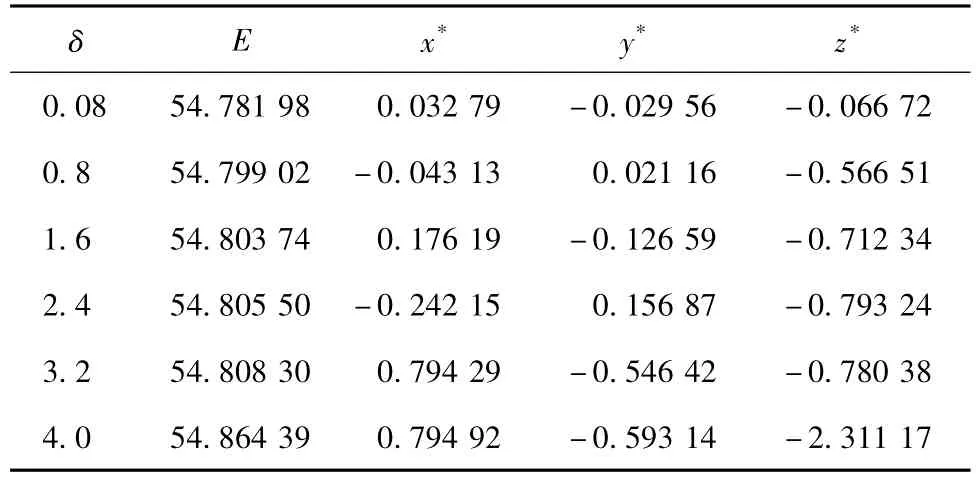
表2 初始态为O点、T=300、‖X‖2≤δ遗传算法求解结果Table 2Maximum prediction errors E and CNOPs yielded bythe genetic algorithm for the modified Lorenz model with the initial basic state O，T=300，and‖X‖2≤δ

由表1和表2可看出，取二范数时，两种方法的计算结果存在较大差异，在最大允许初始误差δ相等的条件下，传统伴随方法所求的最大预报误差小于或等于遗传算法的求解结果。如当δ=1.6时，传统伴随方法所求CNOP为(0.219 03，－0.853 23，－0.561 94)，最大预报误差为35.723 80，遗传算法所求CNOP为(0.176 19，－0.126 59，－0.712 34)，最大预报误差为54.803 74，两CNOP所对应的预报误差和模式y值随时间的发展如图1所示。显然这时传统伴随方法所求的最大预报误差是不可信的，因为当模式含开关时，传统伴随方法可能搜索到全局CNOP(如δ=0.08)，也可能搜索到局部CNOP(如δ=1.6)，而遗传算法总能给出全局CNOP。

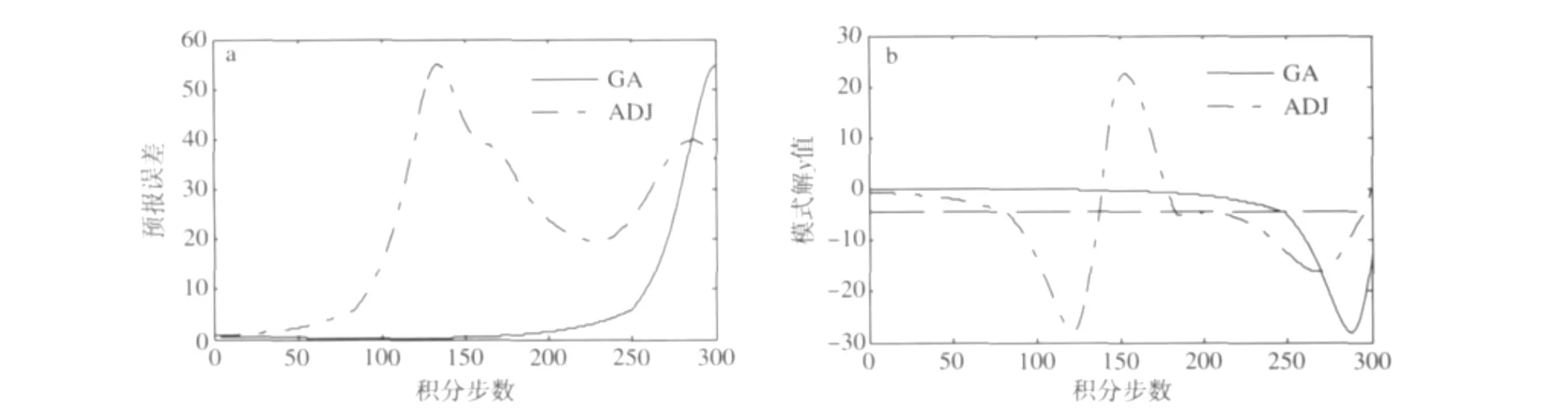
图1 初始态为O点、取二范数、δ=1.6时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.1 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is O，δ=1.6，and the norm is two norm

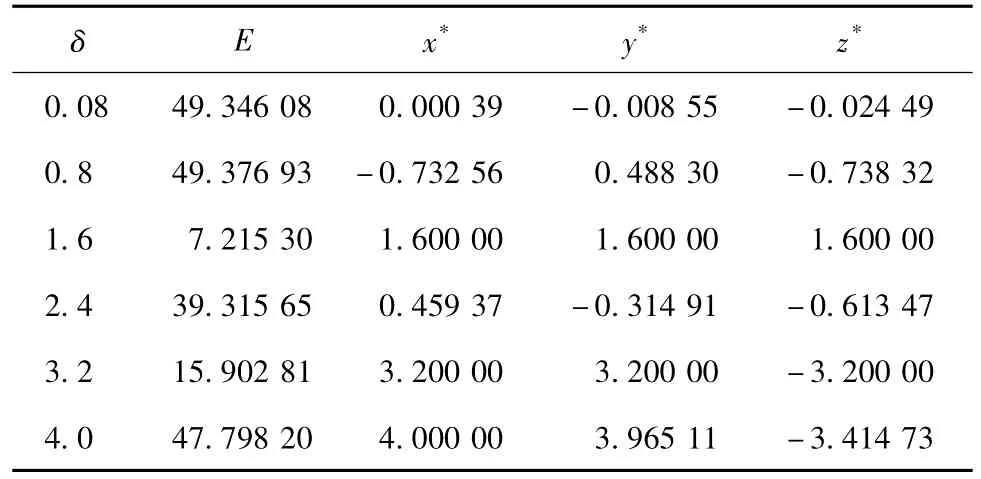
表3 初始态为O点、T=300、‖X‖∞≤δ传统伴随方法求解结果Table 3Maximum prediction errors E and CNOPs yielded by the conventional adjoint method for the modified Lorenz model with the initial basic state O，T=300，and‖X‖∞≤δ

由表3和表4可看出，取无穷范数时，两种方法的计算结果也存在较大差异，如当δ=1.6时，传统

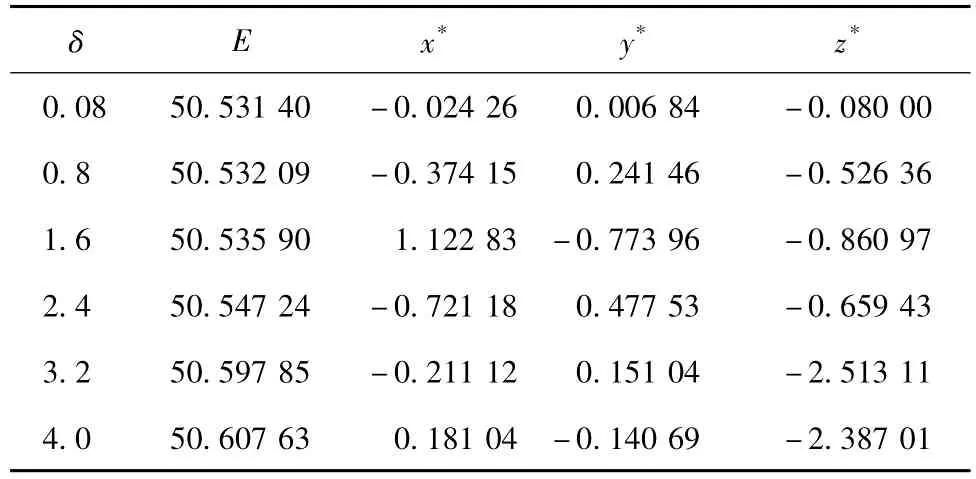
表4 初始态为O点、T=300、‖X‖∞≤δ遗传算法求解结果Table 4Maximum prediction errors E and CNOPs yielded bythe genetic algorithm for the modified Lorenz model with the initial basic state O，T=300，and‖X‖∞≤δ

伴随方法所求CNOP为(1.6，1.6，1.6)，最大预报误差为7.215 30，遗传算法所求CNOP为(1.122 83，－0.773 96，－0.860 97)，最大预报误差为50.535 90，两CNOP所对应的预报误差和模式y值随时间的发展如图2所示，传统伴随方法所求的最大预报误差是不可信的。

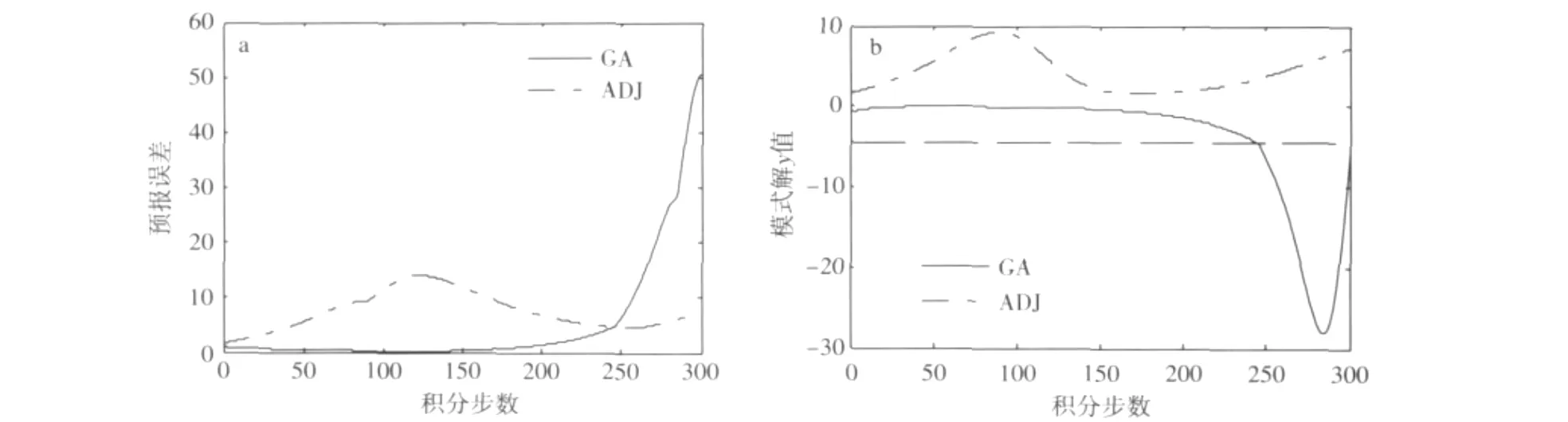
图2 初始态为O点、取无穷范数、δ=1.6时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.2 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is O，δ=1.6，and the norm is infinite norm

4.2 初始基态为C1点

以平衡点C1点为初始态，预报时间步为800，取为二范数，传统伴随方法和遗传算法的求解结果分别由表5和表6给出。

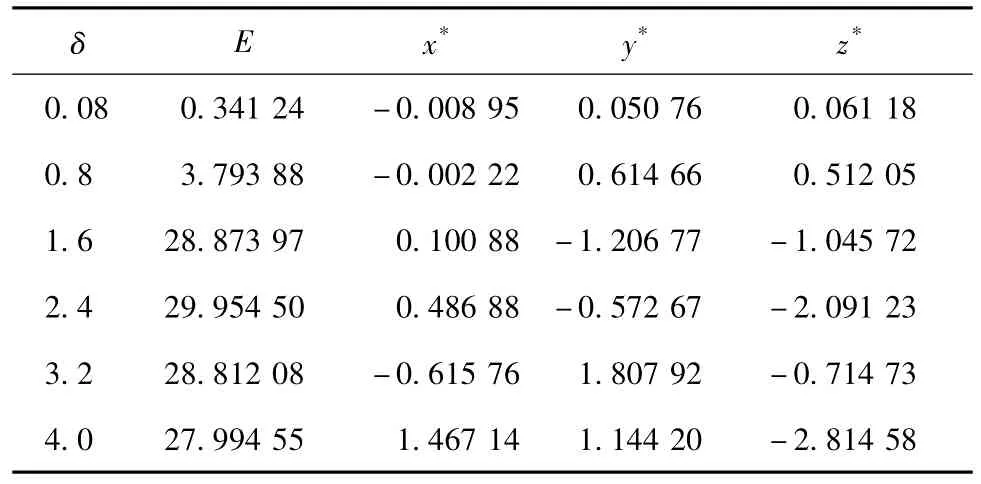
表5 初始态为C1点、T=800、‖X‖2≤δ传统伴随方法求解结果Table 5Maximum prediction errors E and CNOPs yielded bythe conventional adjoint method for the modified Lorenz model with the initial basic state C1，T=800，and‖X‖2≤δ

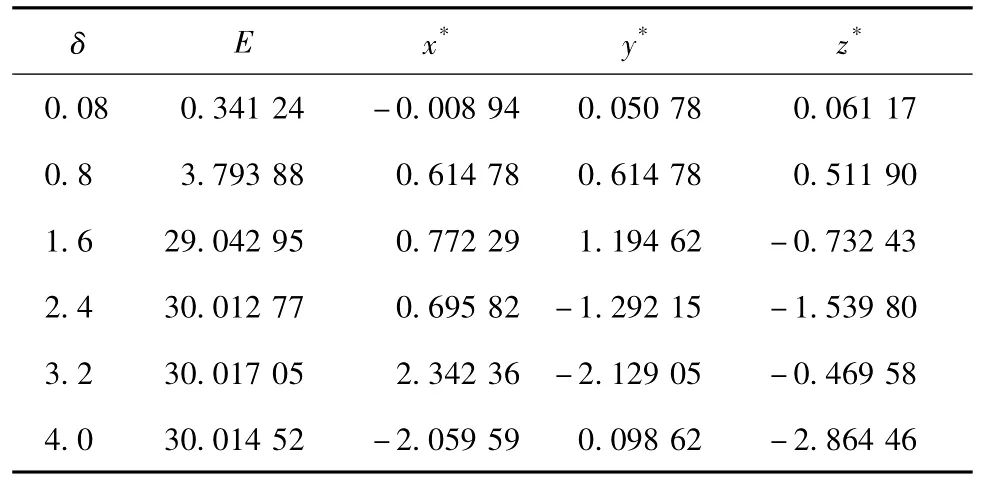
表6 初始态为C1点、T=800、‖X‖2≤δ遗传算法求解结果Table 6Maximum prediction errors E and CNOPs yielded by the genetic algorithm for the modified Lorenz model with the initial basic state C1，T=800，and‖X‖2≤δ

由表5和表6可看出，两种算法的求解结果存在差异，如当δ=3.2时，传统伴随方法所求CNOP为(－0.615 76，1.807 92，－0.714 73)，最大预报误差为28.812 08，遗传算法所求CNOP为(2.342 36，－2.129 05，－0.469 58)，最大预报误差为30.017 05，两CNOP所对应的预报误差和模式y值随时间的发展如图3所示。

同样以C1点为初始态，预报时间步为800，取为无穷范数，传统伴随方法和遗传算法的求解结果分别由表7和表8给出。

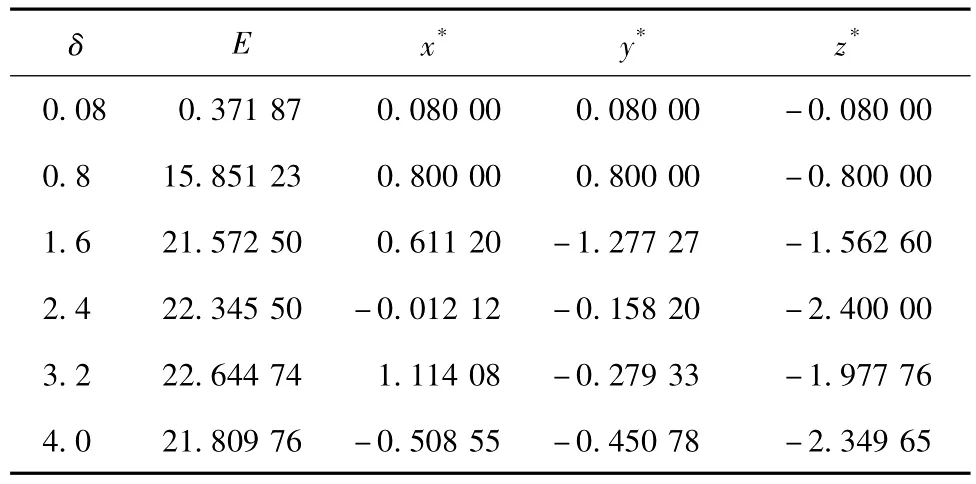
表7 初始态为C1点、T=800、‖X‖∞≤δ传统伴随方法求解结果Table 7Maximum prediction errors E and CNOPs yielded bythe conventional adjoint method for the modified Lorenz model with the initial basic state C1，T=800，and‖X‖∞≤δ

由表7和表8可看出，两种算法的求解结果存在差异，如当δ=3.2时，传统伴随方法所求CNOP为(1.114 08，－0.279 33，－1.977 76)，最大预报误差为22.644 74，遗传算法所求CNOP为(－0.615 52，2.190 31，－1.142 62)，最大预报误差为23.634 55，两CNOP所对应的预报误差和模式y值随时间的发展如图4所示。

图3 初始态为C1点、取二范数、δ=3.2时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.3 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is C1，δ=3.2，and the norm is two norm

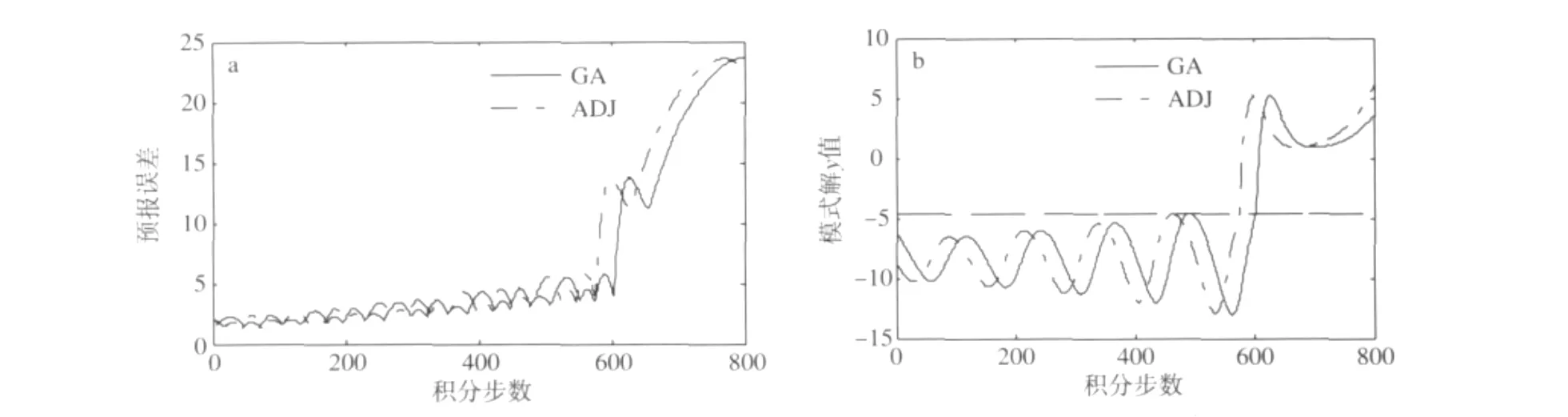
图4 初始态为C1点、取无穷范数、δ=3.2时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.4 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is C1，δ=3.2，and the norm is infinite norm

表8 初始态为C1点、T=800、‖X‖∞≤δ遗传算法求解结果Table 8Maximum prediction errors E and CNOPs yielded by the genetic algorithm for the modified Lorenz model with the initial basic state C1，T=800，and‖X‖∞≤δ

表1 0初始态为A点、T=800、‖X‖2≤δ遗传算法求解结果Table 10Maximum prediction errors E and CNOPs yielded by the genetic algorithm for the modified Lorenz model with the initial basic state A，T=800，and‖X‖2≤δ

4.3 初始基态为A点

以非平衡点A(－6.36，－8.27，21.2)点为初始态，预报时间步为800取为二范数，传统伴随方法和遗传算法的求解结果分别由表9和表10给出。

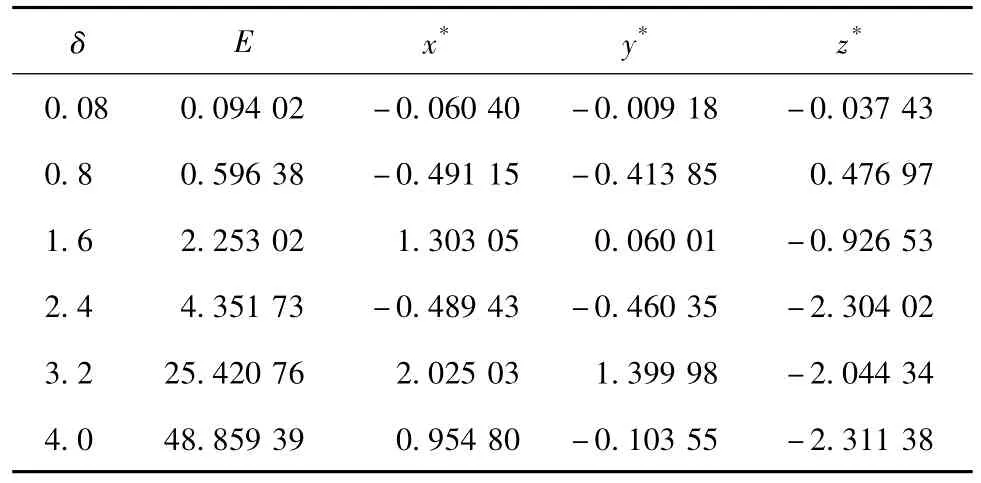
表9 初始态为A点、T=800、‖X‖2≤δ传统伴随方法求解结果Table 9Maximum prediction errors E and CNOPs yielded bythe conventional adjoint method for the modified Lorenz model with the initial basic state A，T=800，and‖X‖2≤δ

由表9和表10可看出，两种算法的求解结果差异较大，如当δ=3.2时，传统伴随方法所求CNOP为(2.025 03，1.399 98，－2.044 34)，最大预报误差为25.420 76，遗传算法所求CNOP为(1.774 67，－0.123 57，－2.064 01)，最大预报误差为48.888 90，两CNOP所对应的预报误差和模式y值随时间的发展如图5所示。

由表11和表12可看出，两种算法的求解结果差异较大，如当δ=3.2时，传统伴随方法所求CNOP为(1.754 87，1.767 44，－1.725 20)，最大预报误差为35.455 56，遗传算法所求CNOP为(2.438 53，0.252 51，－1.832 10)，最大预报误差为38.726 99，两CNOP所对应的预报误差和模式y值随时间的发展如图6所示。

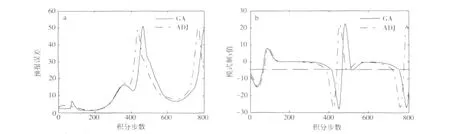
图5 初始态为A点、取二范数、δ=3.2时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.5 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is A，δ=3.2，and the norm is two norm

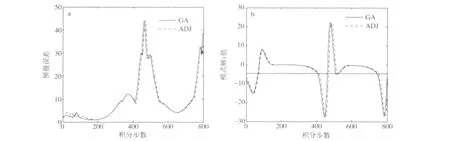
图6 初始态为A点、取无穷范数、δ=3.2时，两CNOP所对应的预报误差(a)和模式y值随时间的发展(b)Fig.6 (a)The prediction errors corresponding to the CNOPs yielded by GA and ADJ，and(b)the time evolution of the component y of the perturbed solution of model(9)when the initial basic state is A，δ=3.2，and the norm is infinite norm

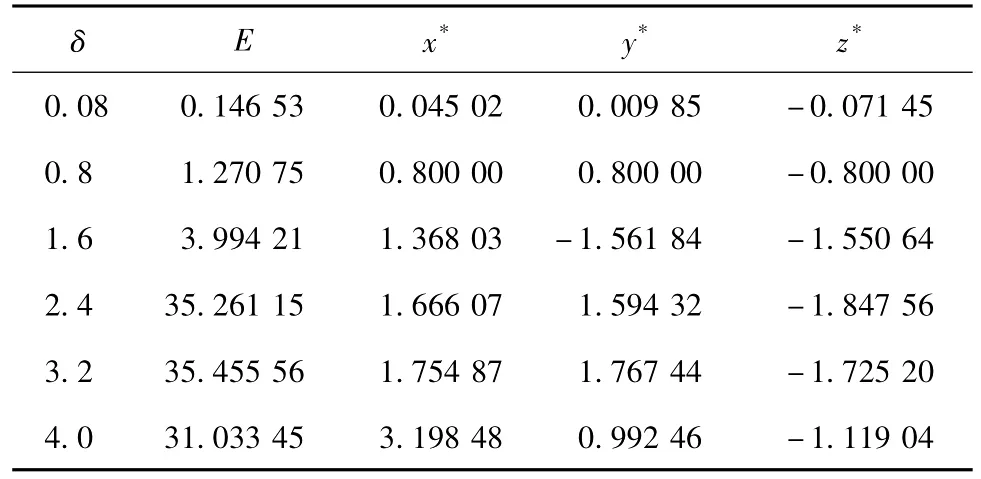
表1 1初始态为A点、T=800、‖X‖∞≤δ传统伴随方法求解结果Table 11Maximum prediction errors E and CNOPs yielded by the conventional adjoint method for the modified Lorenz model with the initial basic state A，T=800，and‖X‖∞≤δ

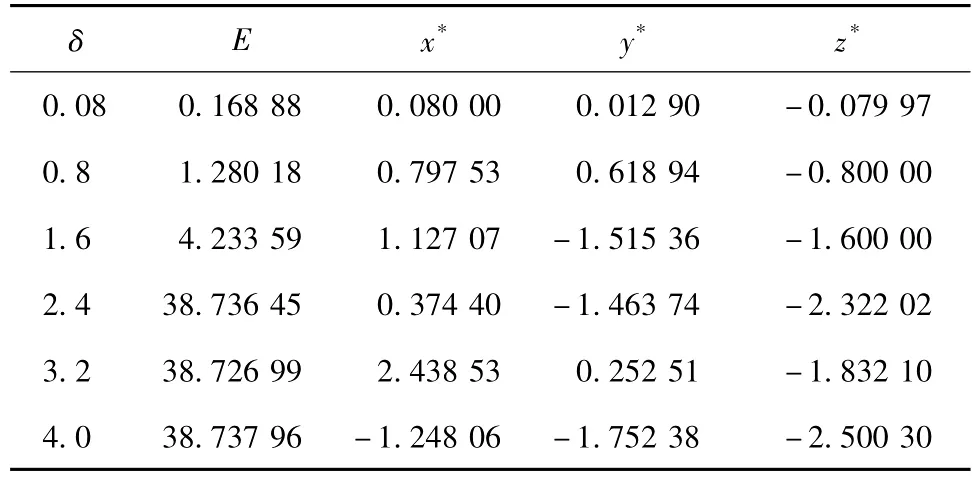
表1 2初始态为A点、T=800、‖X‖∞≤δ遗传算法求解结果Table 12Maximum prediction errors E and CNOPs yielded by the genetic algorithm for the modified Lorenz model with the initial basic state A，T=800，and‖X‖∞≤δ

5 结论

以修改的Lorenz模型为理想模型的数值试验中，初始态无论是平衡点还是非平衡点，初始扰动的度量范数无论是二范数还是无穷范数，在最大允许初始误差δ相等的条件下，传统伴随方法所求的最大预报误差小于或等于遗传算法的求解结果，而且所求的最大预报误差E并不是随最大允许初始误差δ的增大而增大的，说明了当模式存在开关时，代价函数对初值的梯度不存在，传统伴随方法不能为优化过程提供正确的下降方向，导致优化失败，给出的解可能是局部最优解，而遗传算法不受开关的影响，总能给出全局最优解。

遗传算法解决模式含开关时，求解最大预报时间问题的同时，应注意到其计算耗时远大于传统伴随方法，不过遗传算法在迭代过程中，同代的不同个体的遗传操作相互独立，这一特性使得该算法容易实现并行，因此遗传算法向高维模式和实际模式推广时，应考虑并行技术，提高运算效率;另外遗传算法在设计过程中，需要根据模式的具体特点来确定参数，选定遗传操作方案，本文仅采用遗传算法处理约束问题的一般方法来求解，为此探讨新的优化方案，提高算法的收敛速度和计算精度，还需要进一步深入研究。

陈东升，沈桐立，马革兰，等.2004.气象资料同化的研究进展［J］.南京气象学院学报，27(4):550-564.

戴毅，郑琴.2007.具有“on-off”过程的变分资料同化［J］.解放军理工大学学报:自然科学版，8(1):94-98.

胡娅敏，丁一汇，沈桐立.2006.基于遗传算法的四维变分资料同化技术的研究［J］.大气科学，30(2):248-256.

刘巍，张韧，王辉赞，等.2010.分形插值参数的遗传优化及其ARGO海温场应用试验［J］.大气科学学报，33(2):186-192.

石娟，沈桐立，王盘兴.2009.遗传算法同化GPS可降水量资料的研究与应用［J］.气象科学，29(5):584-590.

郑琴，戴毅.2009.非线性扰动方程方法在具有“on-off”振荡的变分资料同化中的可行性［J］.自然科学进展，19(1):81-88.

朱玉祥，苗春生，孙承佼.2006.基于遗传算法的试题库智能组卷系统研究［J］.南京气象学院学报，29(2):282-285.

Deb K.2000.An efficient constraint handing method for genetic algorithms［J］.Comput Methods Appl Mech Engrg，186:311-338.

Duan W S，Mu M.2009.Conditional nonlinear optimal perturbation:Applications to stability，sensitivity and predictability［J］.Science in China Series D:Earth Sciences，52(7):883-906.

Duan W S，Luo H Y.2010.A new strategy for solving a class of constrained nonlinear optimization problems related to weather and climate predictability［J］.Adv Atmos Sci，27(4):741-749.

Fang C L，Zheng Q.2009.The effectiveness of genetic algorithm in capturing conditional nonlinear optimal perturbation with parameterization“on-off”switches included by a model［J］.J Trop Meteor，15(1):13-19.

Fang C L，Zheng Q，Wu W H，et al.2009.Intelligent optimization algorithms to VDA of model with on/off parameterizations［J］.Adv Atmos Sci，26(6):1181-1197.

Lorenz E N.1963.Deterministic nonperiodic flow［J］.J Atmos Sci，20:130-141.

Mu M，Duan W S，Wang J C.2002.The predictability problems in numerical weather and climate prediction［J］.Adv Atmos Sci，19(2):191-204.

Mu M，Duan W S.2003.A new approach to studying ENSO predictability:Conditional nonlinear optimal perturbation［J］.Chin Sci Bull，48:1045-1047.

Mu M，Duan W S，Wang B.2003.Conditional nonlinear optimal perturbation and its application［J］.Nonlinear Processes in Geophysics，10:493-501.

Mu M，Wang J F.2003.An adjoint method for variational data assimilation with physical“On-Off”processes［J］.J Atmos Sci，60:2010-2018.

Mu M，Zheng Q.2005.Zigzag oscillations in variational data assimilation with physical“On-Off”processes［J］.Mon Wea Rev，133:2711-2720.

Mu M，Zhang Z Y.2006.Conditional nonlinear optimal perturbation of a two-dimensional quasigeostrophic model［J］.J Atmos Sci，63(6):1587-1640.

Mu M，Jiang Z N.2007.A new approach to the generation of initial perturbations for ensemble prediction:Conditional nonlinear optimal perturbation［J］.Chin Sci Bull，52:1457-1462.

Tan X W，Wang B，Wang D L.2010.Impact of different guidances on sensitive areas of targeting observations based on the CNOP method［J］.Acta Meteorological Sinica，24(1):17-30.

Wang B，Tan X W.2009.A fast algorithm for solving CNOP and associated targetobservationtests［J］.ActaMeteorSinica，23(4):387-402.

Wang J F，Mu M，Zheng Q.2005.Initial condition and parameter estimation in physical“On-Off”processes by variational data assimilation［J］.Tellus，57A:736-741.

Xu Q.1996a.Generalized adjoint for physical process with parameterized discontinuities，part I:Basic issues and heuristic examples［J］.J Atmos Sci，53:1123-1142.

Xu Q.1996b.Generalized adjoint for physical process with parameterized discontinuities，part II:Vector formulations and matching conditions［J］.J Atmos Sci，53:1143-1155.

Xu Q，Gao J D.1999.Generalized adjoint for physical process with parameterized discontinuities，PartⅥ:Minimization problems in multidimensional space［J］.J Atmos Sci，56:994-1002.

Zheng Q，Mu M.2006.The effects of the model errors generated by discretization of“on-off”processes on VDA［J］.Nonlinear Processes in Geophysics，13(3):309-320.