基于二次函数的模糊数运算

蒲昌玖

（重庆教育学院，重庆400067）

1 引言

模糊数是实数集R上的一类具有与概率分布函数类似性质的特殊模糊集。模糊数之间的加、减、乘、除等四则运算早已有之，如文献［1］、［2］；这些都是基于Zadeh的扩张原理定义的。这些标准模糊运算存在一定的缺陷：随着运算次数的增加，运算后的结果会出现越来越模糊的现象。针对这一缺陷，G.J.Klir于1997年提出了限制模糊运算，主要是研究等式约束关系下的模糊运算，无法给出运算结果的解析表达形式。郭嗣琮［3］利用结构元表示形式有效地解决了模糊数和模糊值函数运算的解析表示问题；杨皎平［4］给出了模糊数在单调函数约束限制的模糊运算，并利用结构元给出了此类模糊运算结果的解析表达形式。

本文主要研究模糊数之间存在二次函数关系限制下的模糊运算，在单调函数约束限制的模糊数运算的基础上，利用模糊结构元，给出了此类模糊数运算的解析表达形式。

2 模糊数定义及标准模糊运算

以往，称实数集R上的正规凸模糊集为模糊数。本文称实数集R上的有界闭模糊数（即正则有界闭凸模糊集）为模糊数，即加上“有界闭”。

定义2.1［1］为有界闭模糊数，当且仅当其隶属函数

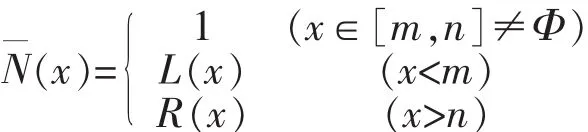
定义2.2［5］设A∈F（U），Supp A＝｛x∈U｜A（x）≠0｝叫Fuzzy集A的支撑集。

根据扩张原理，模糊数的四则运算可以定义如下：

定义2.3［2］设，为两个模糊数，隶属函数分别为（x）（y），设的支撑集为X，的支撑集为Y，x∈X，y∈Y，标准模糊运算被定义为（*）（z）＝

3 限定关系下的模糊数运算

R（*）（z）中*∈｛+，-，×，÷｝。

性质1［4］设、为同一模糊数，设x∈，y∈，R：x＝-y，则R（-）＝0。

通过性质1知，在限定关系下的模糊数运算解决了标准模糊运算与自己的差不为0的缺陷。

例1设一个作业有两个部分组成，完成第一个部分的时间为A＝（0.6 0.8），完成第二部分的4 6时间为B＝（0.8 0.6），求完成整个作业的天数（A、6 8 B是模糊数）。

从以上的计算可以看出，标准模糊运算所得结果的模糊度比原先增加了；而限定关系下模糊运算的结果并不存在这样的问题。出现这样的问题的原因是标准模糊运算没有考虑模糊数之间存在的关系。

3.1 用结构元表示限定关系下的模糊运算

定义3［3］设E为实数R上的模糊集，隶属函数记为E（x），x∈R。如果E（x）满足下述性质：

（1）E（0）＝1，E（1+0）＝E（-1-0）＝0；

（2）在区间［-1，0）上E（x）是单增左连续函数，在区间（0，1］上是单降右连续函数；

（3）当-∞＜x＜-1或者1＜x＜+∞时，E（x）＝0。则称模糊集E为R上的模糊结构元。

若模糊结构元E满足：

（1） 对于∀x∈（-1，1），E（x）＞0；

（2） 在区间［-1，0）上E（x）是连续且严格单调增的，在区间（0，1］上是连续且严格单调降的。则称E为正则模糊结构元。

文中讨论的模糊结构元均为正则模糊结构元，为简便起见都简称为模糊结构元。

定理3.1［6］（局部映射原理）设E是R上模糊结构元，具有隶属函数E（x），由设f（x）在区间［-1，1］上是连续、单调，则模糊结构元E的模糊变换f（E）是模糊数，且f（E）的隶属函数为E（f-1（x）），这里f-1（x）是f（x）的反函数。

定理3.2［1］对于给定的正则模糊结构元E和任意的有界闭模糊数A，总存在一个在［-1，1］上的单调有界函数f，使得A＝f（E）。

设E1、E2为模糊结构元，隶属函数为E1（x）、E2（y）。设x，y∈［-1，1］，存在限定关系xRy，则可得用结构元表示的限制关系下的模糊运算公式为［4］：其中*∈｛+，-，×，÷｝，限定关系R有函数关系、不等式关系甚至是概率关系等等。

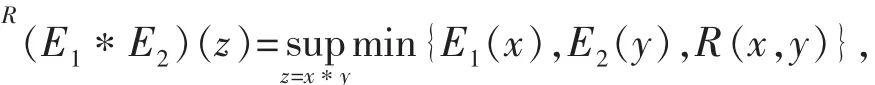
杨皎平［4］等给出了单调函数约束限制下模糊运算结果的解析表达形式，在实际运用中具有重要的意义。本文主要研究二次函数限制关系下的模糊数运算。y＝x2无疑是最简单的二次函数，下面讨论基于y＝x2限制条件下的模糊数的运算。

命题1［4］对模糊数A、B，设A的支撑集为X，B的支撑集为Y，A的隶属函数为A（x），B的隶属函数为B（x），如果满足下面条件，则有B＝R（A），

（ⅰ）R（x）为X上的单值单调有界函数，Y为其值域。

（ⅱ）如果y＝R（x），那么A（x）＝B（y）。

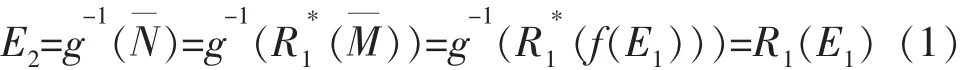
其中R1为［0，1］上的单调有界函数。

命题3当x、y∈［-1，0］，且存在关系R（x，y）：y＝x2，设f、g和是［-1，0］上的单调有界函数，E1、E2为

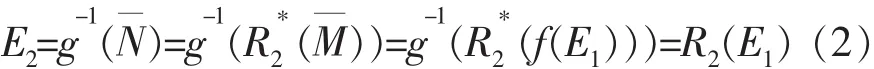
其中R2为［-1，0］上的单调有界函数。

定理3.3设E1、E2为模糊结构元，如果f和g分别是［-1，0］和［0，1］上的两个单调函数，＝f（E1），＝g（E2），R（x，y）：y＝x2，如果满足下面条件，则有：

R（E1*E2）（z）＝E1（（fgR1）-1（z））*E2（（fgR2）-1（z）），其中*∈｛+，-，×，÷｝。

（ⅰ）R（x）为E1的支撑集上的单调有界函数，E2的支撑集为其值域。

（ⅱ）如果y＝R（x），那么E1（x）＝E2（y）。

证明记限制关系R（x，y）：y＝x2在区间［0，1］上为R1，在区间［-1，0］上为R2。

（1）由于f、g和R1是［0，1］上的单调有界函数，所以f（x）*g（R1（x））也为单调有界函数。根据结构元表示的限制关系下的模糊运算公式，得出：

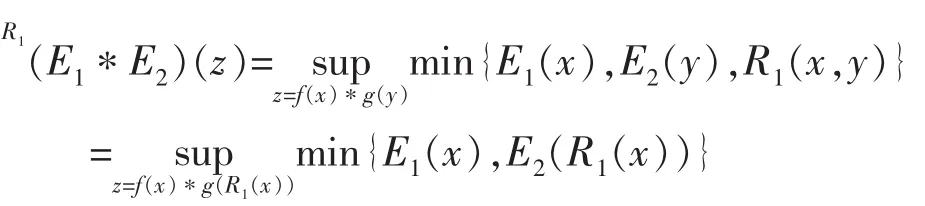
＝E1（（fgR1）-1（z））（因f、g和R1是［0，1］上的单调有界函数）

（2）由于f、g和R2是［-1，0］上的单调有界函数，所以f（x）*g（R2（x））也为单调有界函数。根据结构元表示的限制关系下的模糊运算公式，得出：

＝E1（（fgR2）-1（z））（因f、g和R2是［-1，0］上的单调有界函数）

综合（1）和（2）：

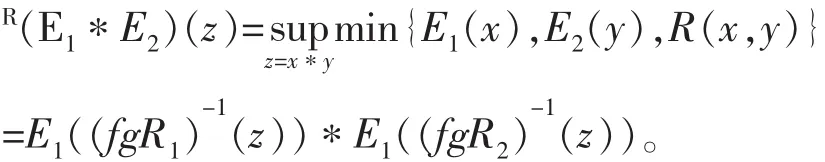
对两个满足二次函数限定关系的模糊数的运算，可以分成两部分，分别根据命题2和命题3来得到两个结构元之间的关系表达式，再根据定理3.3计算得出最后的结果。在实际问题中，大多的情况不是y＝x2这样简单的二次关系，但总可以通过平移来达到这样的条件。对于任意一个模糊数，也总可以通过线性变换将其变成一个模糊结构元。模糊数之间的限定关系也可以通过线性变换为结构元之间的限定关系。

例2设A＝3+5E1，B＝4+8E2，设A的支撑集为X，B的支撑集为Y，对x∈X，y∈Y，满足函数关系R：y＝x2，求R（A+B）解。

解：（1）当x∈［0，1］，R：y＝x2为单值单调有界函数，根据命题1，得B＝R（A）＝（A）2，根据命题2得：

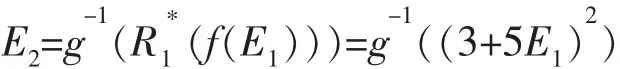
4 结论

限定关系下的模糊运算能很好地解决标准模糊数运算存在的缺陷，在原有理论的基础上，利用了模糊结构元，并给出了运算因子之间存在二次函数关系限制下的模糊运算结果的表达形式。通过例1验证了表达形式的有效性，为实际应用奠定了一定的理论基础，具有重要的意义。

［1］罗承忠.模糊集引论［M］.北京：北京师范大学出版社，1989.

［2］张文修等.模糊数学引论［M］.西安：西安交通大学出版社，1991.

［3］郭嗣琮.模糊值函数分析学的结构元方法简介（Ⅰ）-结构元与模糊数运算［J］.数学的时间与认识，2008，38（2）：87～93.

［4］杨皎平，高雷阜.单调函数限定下的模糊算子的研究［J］.科学技术与工程，2005，5（2）：65～68.

［5］徐宗本，张讲社，郑亚林.计算智能中的仿生学：理论与算法［M］.北京：科学出版社，2003.

［6］郭嗣琮.模糊分析中的结构元方法（Ⅰ）［J］.辽宁工程技术大学学报，2002，21（5）：670～673.