一种用于单周期控制的斜率自适应积分电路的设计
2011-01-29电子科技大学电子薄膜与集成器件国家重点实验室余清华
电子科技大学电子薄膜与集成器件国家重点实验室 宋 健 代 杰 余清华
一种用于单周期控制的斜率自适应积分电路的设计
电子科技大学电子薄膜与集成器件国家重点实验室 宋 健 代 杰 余清华
采用电流模相乘器结构,同时结合计数器,设计了一种结构简单、斜率自适应、高精度的积分器,具有良好的线性特性,线性范围达到0~6V,能够广泛应用在固定开关频率的单周期控制的功率因数校正芯片中。此外,还对负反馈电路的稳定性和频率补偿进行了讨论和仿真,得到了约78度的相位裕度。最后给出了具体的积分器电路图和仿真结果。
单周期控制;电流模相乘器;计数器;积分器
1.引言
在开关电源领域,任何使输入电网电流为非线性,或即使是正弦波但和正弦输入电压不同相位,或使输入电流具有谐波的电路结构都会降低功率因数从而产生额外的功率损耗。为了提高对电能的利用效率,需要引入功率因数校正技术[1]。
传统的功率因数校正电路技术复杂,步骤繁琐,体积大,成本高,而单周期控制技术是一种非线性控制技术,不但大大简化了电路而且使得电路的抗干扰能力、鲁棒性、动态响应更好[2]。单周期控制的控制策略是对控制信号进行积分后与基准信号进行比较,决定开关的占空比。
本文中的积分器将控制电压转换成电流后,利用双极型晶体管的电流-电压指数关系,构成一个自动调节尾电流源的模拟乘法器,再利用电流对电容充电实现积分,能够很好地应用在各类单周期控制的PFC芯片中。
2.积分器的原理分析
本文中所设计的积分器是在电流模相乘器[3]的基础上加以改进,利用电流对电容充电实现积分的功能。首先给出单周期控制PFC的原理[4]。

式(7)、(8)为单周期控制方程组。其中Vm是系统控制电压,ig是输入电流,RS是输入电流检测电阻。实际上,V2(t)是对Vm在整个周期内积分,当V1(t)和V2(t)相等时,通过PWM比较器可以确定开关的占空比D。从(8)式可知单周期控制的核心在于对Vm进行积分。因此,需要构建一个积分器。
如图1所示为本文设计的积分器的整体电路图,其中电源电压VCC=7.5V,VIN是输入电压,即为式(8)中的控制电压Vm,VBIAS1、VBIAS2是固定偏置电压,VPULSE是每个周期对积分器进行复位的脉冲,VOUT是积分器的输出。
Q34、Q35、Q36、Q37和R18构成电流基准源,其中Q35、Q36、Q37相同,Q34的面积是他们的4倍。Q27、Q28、Q29、Q30、Q31、Q32、Q33和R17产生稳定的偏置电压VBIAS1。Q1、Q2、Q3、Q4构成电流模相乘器,Q5、Q7、Q9、R1、R2与Q6、Q8、Q10、R3、R4分别构成威尔逊电流镜,忽略基极电流影响,则有


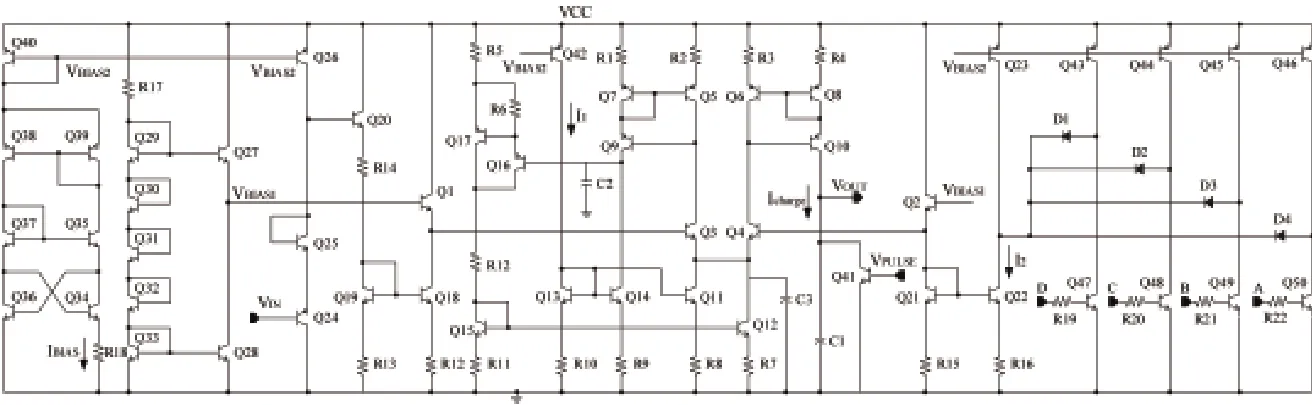
图1 积分器整体电路图
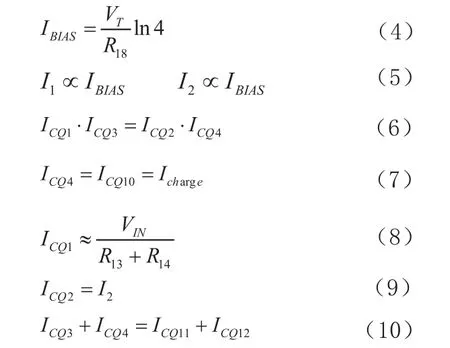
Q12、Q15、Q16、Q17、R5、R6、R7、R11、R12、C2、C3构成负反馈回路,随着输入电压VIN的变化自动调节Q12中电流的大小,同时维持Q9和Q14中流过的电流相等,因此
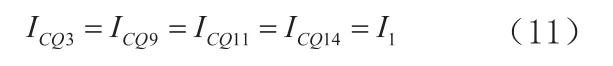
将式(7)、(8)、(9)、(11)代入式(6)得到

对比式(2)与式(13),只要使
.即可满足要求,一个周期内使得积分器输出VOUT=VIN。因此只要根据PFC的工作频率来设计 的值,就能得到满足要求的积分电路。
由于电路性能会受温度、电源电压和各种工艺参数的影响,导致不可能得到一个精确的 。因此,需要设计一个模16可逆型计数器来自动调整 值的大小,1/即为积分斜率。图1中,Q43~Q50、D1~D4和R19~R22组成四个开关,根据计数器的4位输出来改变I2的大小,来积分斜率。其中Q23、Q43、Q44、Q45、Q46的面积之比为8:2:1:0.5:0.25。
可逆计数器控制由图2给出。通过一个比较器,对VOUT和VIN进行比较,如果VIN>VOUT,比较器输出高电平,控制计数器正向计数,I2变小,积分斜率变大,VOUT将会变大;如果VIN<VOUT,计数器逆向计数,I2变大,积分斜率变小,VOUT将会变小。这样,通过一个可逆计数器就实现了对积分器斜率的自动调整。
3.积分器的仿真
3.1 积分器输出随输入电压变化
如图3所示为积分器输出随输入电压变化的仿真图。其中VIN时斜坡电压,VOUT为积分输出的锯齿波电压。图4是积分器输出随输入电压变化局部放大图,可以看到,积分输出VOUT的峰值与积分输入VIN基本重合,积分效果理想。
从仿真得到VIN=5.6V时,VOUTPEAK=5.625V,计算得到精度为
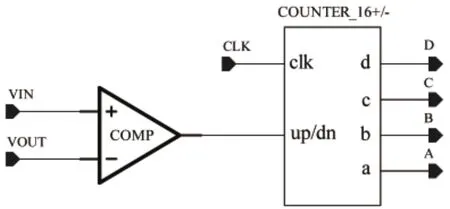
图2 可逆计数器控制电路
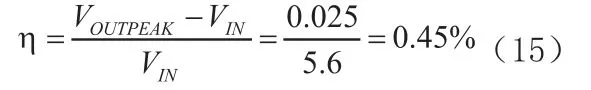
3.2 电路稳定性的分析和仿真
当电路存在负反馈时,如果相位裕度太小,会在较高频率扰动时造成系统的不稳定。根据文献[5]的说明,当相位裕度为60°时,闭环频率响应的尖峰已可忽
略。如图1所示,Q12、Q15、Q16、Q17、R5、R6、R7、R11、R12、C2、C3构成负反馈回路,因此必须对其稳定性进行考虑。随着输入电压VIN的变化反馈回路自动调节Q12中电流的大小,使得积分电流变化,始终保持与输入电压VIN成正比。因此对积分器反馈回路的稳定性进行仿真很重要。
反馈回路中Q16的基极为一个高阻节点,因此加电容C2到地,引入一个低频主极点,使得环路增益下降点提前,幅频曲线增益交点提前,提高了环路相位裕度。当加上C3后在高频引入极点,使得高频增益下降变快,抑制高频噪声的影响。环路的频率响应曲线如图5所示,环路增益约为60dB,其相位裕度约为78°,系统的稳定性很好。
3.3 积分电流的仿真
由于负反馈的调节,尾电流源Q12中的电流会随着输入电压VIN的变化而变化,实现积分电流Icharge跟随输入电压变化。对输入电压VIN进行DC扫描,范围从0~7V,观测Q10中的充电电流变化。从图6的仿真结果可以看到,积分电流Icharge随着输入电压VIN的增大而增大,并且与VIN成正比。仿真结果验证了式(12)中推导的Icharge与VIN的正比关系。当VIN>6V时,Icharge达到饱和,所以输入电压的范围在0~6V。
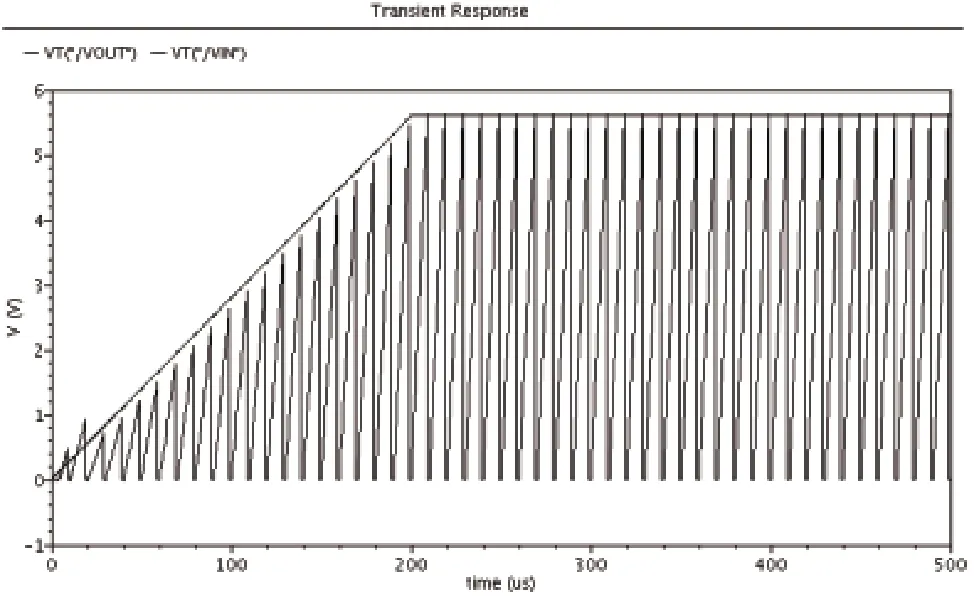
图3 积分器输出随输入电压变化的仿真图
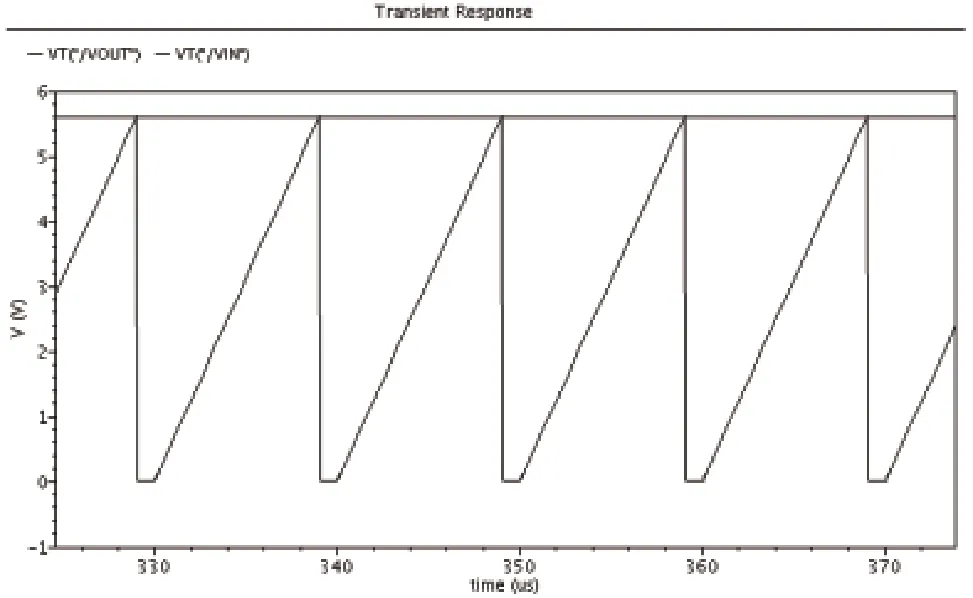
图4 积分器输出随输入电压变化局部放大图
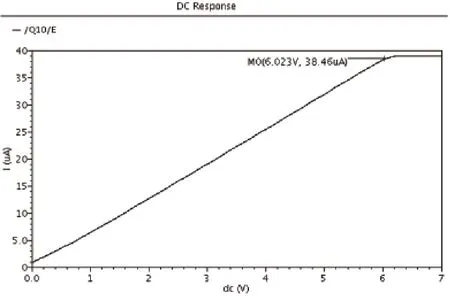
图6 积分电流随输入电压的变化关系
4.结论
本文所设计的积分器采用电流模相乘器的结构,同时结合可逆计数器控制,实现了斜率自适应功能。利用稳定的负反馈结构以保证积分器在不同输入电压下都能精确地实现对输入电压进行积分的功能。通过仿真结果表明,积分器的输入电压范围大,稳定性良好,精度高,适用于单周期控制的PFC芯片。
[1]Abraham I.Pressman,Keith Billings,Taylor Morey.Switching Power Supply Design[M].Third Edition,New York:McGraw-Hill Company,2009:671-672.
[2]Keyue M.Smedley,Slobodan Cuk.One-Cycle Control of Switching Converters[J].IEEE Transactions on Power Electronics,1995,10(6):625.
[3]周柏毓.一种双环控制的连续电流模式功率因数校正控制器设计[D].成都:电子科技大学微电子与固体电子学院,2007.
[4]胡新新,郭育华.基于IR1150的有源功率因数校正电路的设计[J].自动化信息,2008,11:35.
[5]毕查德拉扎维著.陈贵灿,程军,张瑞智译.模拟CMOS集成电路设计[M].西安:西安交通大学出版社,2003:289-315.
宋健(1986—),男,江苏苏州人,硕士研究生,主要研究方向:模拟集成电路设计。
代杰(1986—),男,四川富顺人,硕士研究生,主要研究方向:模拟集成电路设计。
余清华(1987—),男,福建宁化人,硕士研究生,主要研究方向:模拟集成电路设计。
