极小化两种目标函数的具有学习效应的单机排序问题
2011-01-29娄宗山
娄 敏,娄宗山
(1.曲阜师范大学管理学院,山东日照 276826;2.山东省诸城第一中学,山东诸城 262200)
最近几年来,关于学习效应的排序问题受到了国内外许多学者的广泛关注.在经典的排序理论中,工件的加工时间通常都被看做是一个固定的常数.然而,在许多现实情况中,如机器或工人反复或连续加工相同或类似的工件时,由于他们能从中学习到如何更加有效的完成工件的生产,因此越在后面的工件它所需要的加工时间就越少,这种现象就是“学习效应”.
唐国春等[1]对现代排序问题的10个分支进行了系统详细的讨论.Biskup[2]首次将学习效应应用于排序问题当中,他提出了一个工件的加工时间与工件所在位置有关的学习效应模型;在单机条件下,他研究了目标函数为极小化总完工时间的排序问题,得到了工件按照规则排列获得最优排序.Yang和Kuo[3]对于Biskup[2]提出的学习效应模型研究了具有学习效应的间歇批生产的单机排序问题,并且给出了目标函数为极小化最大完工时间这一问题的多项式时间算法.Kuo和Yang[4-5]给出一种与时间有关的学习效应模型并且进行了深入研究,给出了相应的多项式时间算法.王吉波等[6-7]继续对带学习效应的排序问题进行了探讨,将安装时间,恶化效应等应用到带学习效应的排序问题中,并且给出了最优算法.
本文研究了具有学习效应和遗忘效应的间歇批生产的单机排序问题,分别讨论批与批之间没有学习效应的传递,批与批之间有部分学习效应的传递这两种情形是多项式可解的,针对批与批之间有总的学习效应传递的情形,我们给出了在每一批内工件个数都相等这一特殊情形下的多项式时间算法.
1 符号表示
m表示批的个数,m≥2;
Bi表示第i批,i=1,2,…,m; ni表示第i批的工件个数,i=1,2,…,m; n表示工件的总个数,n1+n2+…+nm=n; Jij表示第i批中的第j个工件,j=1,2,…,ni;
ai表示Bi内工件的学习因子,0<ai≤1;
bi表示Bi的学习因子,0<bi≤1;
pij表示工件Jij的正常加工时间;
pr表示工件J在B中排在第r个位置上加工的实际加工时间;ijiji
pi[k]表示工件Ji[k]在Bi中排在第k个位置上加工的正常加工时间;
pk表示工件J在B中排在第k个位置上加工的实际加工时间;i[k]i[k]i
Cij表示工件Jij的完工时间;
Ci[k]表示工件Ji[k]在Bi中排在第k个位置上加工的完工时间;
Cmax表示所有工件的最大完工时间;为所有工件的总完工时间.
所有n个工件被分成m批放在一台机器上进行加工,并且所有工件在0时刻都是准备就绪的.如果工件被安排在第一批的第一个位置上进行加工,那么它的实际加工时间就是它的正常加工时间.由于学习效应的存在,被加工的工件越往后,它所需要的加工时间就越少.为描述方便,我们用LE表示学习效应;B表示间歇的批生产问题.定义,其中α,β,ai均为常数,且满足α≥0,β≥0,α+ β=1,0<ai<1.
然而,如果生产线之间中断的时间比较长,那么可能会出现遗忘效应,即可能出现批与批之间没有学习效应的传递,有部分学习效应的传递,有总的学习效应的传递这样三种情形.下面两部分分别对两种目标函数下的情形进行探讨.
2 极小化最大完工时间
2.1 批与批之间没有学习效应的传递
Jij被安排在Bi中的第r个位置上加工的实际的加工时间表示为prij=pij(αari-1+β).因此,若Bi在第i批加工,那么所有工件的最大完工时间为).用Tno表示批与批之间没有学习效应的传递,因此根据排序理论中经典的三参数表示法将该问题记为:1|B,LE,Tno|Cmax.
引理1 对于问题1|LE|Cmax的最优排序可以通过工件的正常加工时间的SPT规则得到.
定理1 对于问题1|B,LE,Tno|Cmax存在一个最优排序满足下面两个条件:
(1)对于每一批内的工件,按正常加工时间的SPT规则排列;
(2)批与批之间按照任意次序在机器上加工.
证明(1)每一批内的工件的最优排序问题等价于问题1|LE|Cmax,根据引理1,按工件的正常加工时间的SPT规则排列即可得最优排序.
(2)批与批之间没有学习效应的传递,因此批的加工时间并不受其所在位置的影响,所以批与批之间按照任意次序在机器上加工即可.
下面给出求解问题1|B,LE,Tno|Cmax的最优算法:
算法2.1 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 批与批之间按照任意次序在机器上加工.
在第1步中,将Bi内的工件按照SPT规则排列,其时间复杂性为O(nilog ni),那么对所有批内的工件排序花费时间为iΣm=1O(nilog ni),所以第1步的时间复杂性为O(n log n);第2步,批与批之间按照任意次序排列花费时间为O(1),因此算法A的时间复杂性为O(n log n).
2.2 批与批之间有部分学习效应的传递
假设每一批内的工件的学习效应与2.1一致.定义Bi被安排在第r批加工的实际加工时间:Pir= Pi(αbri-1+β),其中Pi为Bi内的工件按照SPT规则排序的完工时间,并且Pi不受批所在位置的影响.若Bi在第i批加工,于是有
用Tpart表示批与批之间有部分学习效应的传递,那么该问题用三参数表示法记为1|B,LE,Tpart| C.
max记|C,那么问题1|B,LE,Tpartmax的批的加工次序问题可转化为下面的指派问题来求解:
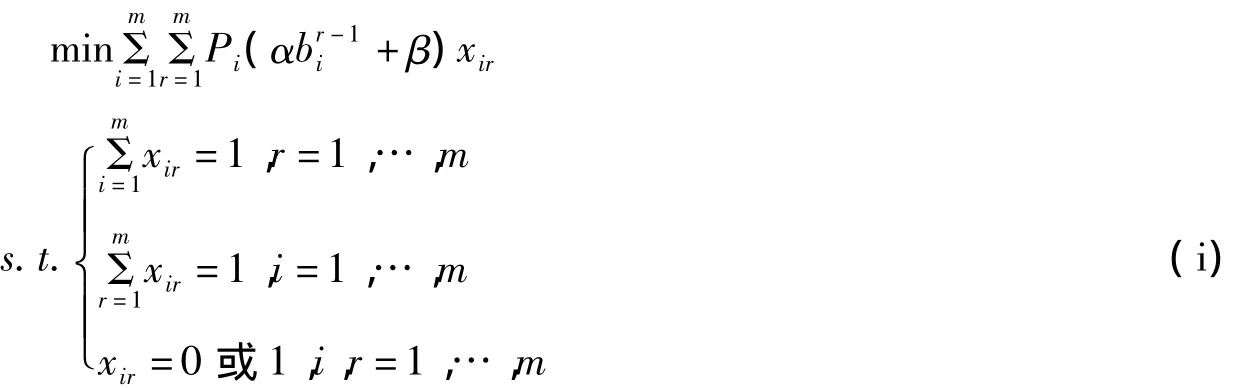
下面给出求解问题1|B,LE,Tpart|Cmax的最优算法:
算法2.2 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 根据指派问题(i)来安排批的加工次序.
第1步的时间复杂性为O(n log n),第2步求解指派问题花费的时间是O(m3),因此算法2.2的时间复杂性为O(n log n+m3).
推论1 若所有批的学习因子都相等,即bi=b(i=1,…,m),那么对于问题1|B,LE,Tpart|Cmax存在一个最优排序满足下面两个条件:
(a)对于每一批内的工件,按正常加工时间的SPT规则排列;
(b)批与批之间按照Pi不减的顺序排列.
证明 (a)对于每一批内的工件,根据引理1可知按照SPT规则得到最优排序;
(b)如果所有批的学习因子都相等,那么可以将每一批看做一个工件,批的完工时间Pi作为Bi的加工时间,因此问题1|B,LE,Tpart|Cmax等价于问题1|LE|Cmax,根据引理1知按照Pi不减的顺序排列即可得最优排序.
由推论1知,(a)的时间复杂性为O(n log n);(b)中对批的次序排列需花费时间O(m log m),由于n>m,因此在bi=b(i=1,…,m)这一特殊情形下,问题1|B,LE,Tpart|Cmax的时间复杂性为O(n log n).
2.3 批与批之间有总的学习效应的传递
不失一般性,我们假设Bi是在第i批加工,那么Bi中的工件Jij在第r个位置上加工时,其实际加工时间为,因此有.用T表示批与批之间有总的total学习效应的传递,那么该问题用三参数表示法记为1|B,LE,Ttotal|Cmax.
定理2 对于问题1|B,LE,Ttotal|Cmax,每一批的最大完工时间的最优值可以按工件的正常加工时间的SPT规则排列得到.
证明 假设π为一最优排序,对于Bi中的两个工件Jij和Jil,满足pij≥pil,Jij在Bi中的第r个位置上加工,Jil在Bi中的第r+1个位置上加工.令s为第r-1个位置上工件的完工时间,B为在Jij和Jil之后加工的工件的加工时间之和.
交换工件Jij和Jil的位置得到一个新的排序π',π'中交换Jij和Jil的位置后s和B不变
由α≥0,β≥0,α+β=1,0<ai≤1知.因此有
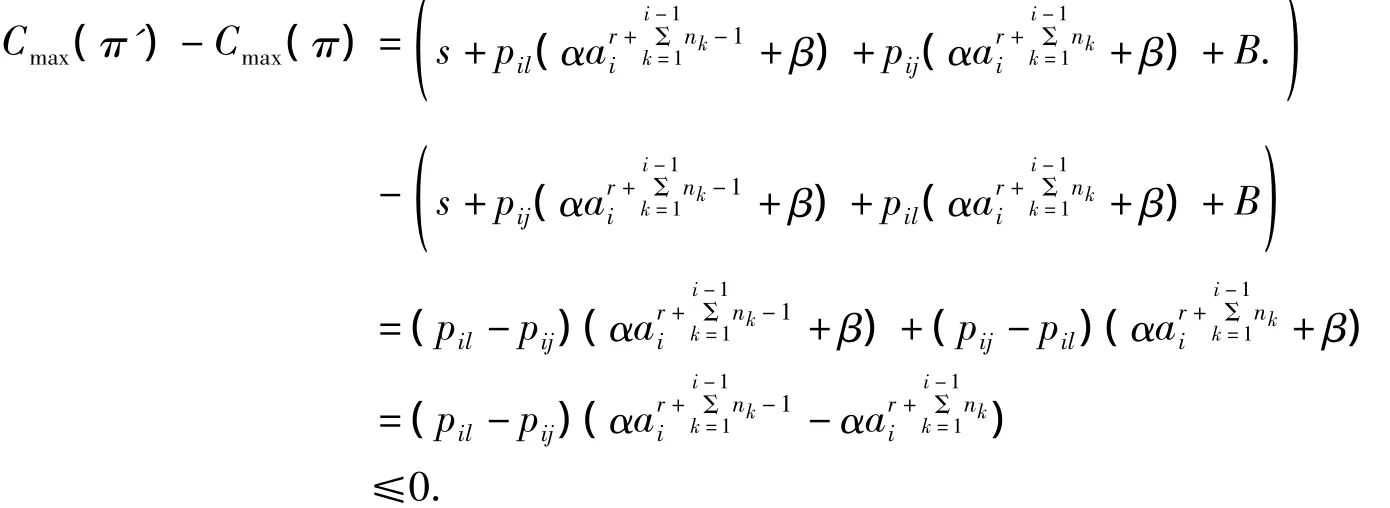
这说明π'也是最优排序.对π中不满足SPT规则排序的工件进行调整,直到它们都满足SPT序为止,由此得到满足定理的最优排序.
推论2 对于问题1|B,LE,Ttotal|Cmax,存在一个最优排序使得每一批内的工件都按正常加工时间的SPT规则排列.
下面我们讨论问题1|B,LE,Ttotal|Cmax的两种特殊情况:
第1种特殊情况:
定义1 Bi≺Bj表示Bi被Bj支配或者Bj支配Bi:
如果
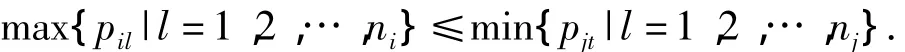
定义2 如果B1≺B2≺…≺Bm,就说形成了支配批的增序.
定理3 若B1≺B2≺…≺Bm并且a1=a2=…=am,那么对于问题1|B,LE,Ttotal|Cmax存在一个最优排序满足下面两个条件:
(a)对于每一批内的工件,按正常加工时间的SPT规则排列;
(b)批与批之间按支配批的增序排列.
第2种特殊情况: =n=…=n=¯n如果每一批内工件的个数都相等,即n12m,记,则问题1|B,LE,Ttotal|Cmax的批的加工次序问题可转化为下面的指派问题来求解:
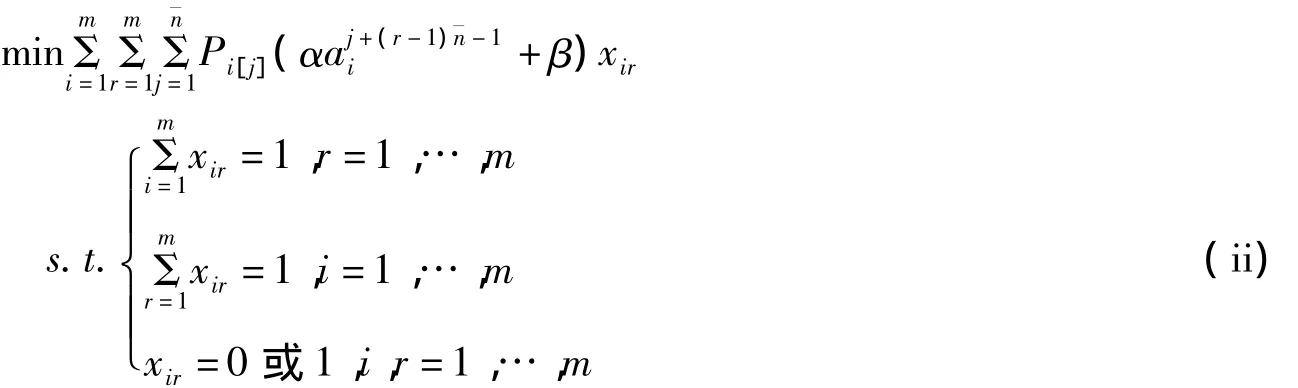
下面给出当n1=n2=…nm=¯n时,求解问题1|B,LE,Ttotal|Cmax的最优算法:
算法2.3 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 根据指派问题(ii)来安排批的加工次序.
算法2.3的时间复杂性为O(n log n+m3).
3 极小化总完工时间
3.1 批与批之间没有学习效应的传递
根据排序理论中经典的三参数表示法将该问题记为:1|B,LE,Tno|ΣΣCij.
引理2 对于问题1‖ΣCj,其最优排序可以通过SPT规则得到.
引理3 对于问题1|LE|ΣCj的最优排序可以通过正常加工时间的SPT规则得到.
记P为B按照SPT规则排序的完工时间ii,下面我们给出求解问题1|B, LE,Tno|ΣΣCij的最优算法:
算法3.1 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 批与批之间按照Pi非减的次序在机器上加工.
算法3.1的时间复杂性为O(n log n).
定理4 算法3.1最优的解决了问题1|B,LE,Tno|ΣΣCij.
证明 对于每一批内的工件的最优排序问题等价于问题1|LE|ΣCj,根据引理3,每一批的工件按照正常加工时间的SPT规则排序即可得最优排序.
因为批与批之间没有学习效应的传递,所以可以把每一批看做一个工件,批的完工时间Pi作为Bi的加工时间,则问题1|B,LE,Tno|ΣΣCij等价于问题1‖ΣCj,那么由引理2知,批与批之间按照Pi不减的顺序排列即可得最优排序.
3.2 批与批之间有部分学习效应的传递
假设每一批内的工件的学习效应与3.1一致.定义Bi被安排在第r批加工的实际加工时间:Pir=,其中为Bi内的工件按照SPT规则排序的完工时间,并且Pi不受批所在位置的影响.记Ci表示在批与批之间没有学习效应传递的情况下每一批内的所有工件的总完工时间,有该问题用三参数表示法记为1|B,LE,Tpart|ΣΣCij.
记
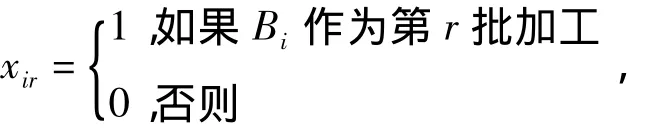
那么问题1|B,LE,Tpart|ΣΣCij的批的加工次序问题可转化为下面的指派问题来求解:

算法3.2 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 根据指派问题(iii)来安排批的加工次序.
算法3.2的时间复杂性为O(n log n+m3).
定理5 算法3.2最优的解决了问题1|B,LE,Tpart|ΣΣCij.
推论3 如果所有批的学习因子都相等,即bi=b(i=1,…,m),那么对于问题1|B,LE,Tpart|ΣΣCij,算法3.1为最优算法.
证明 对于每一批内的工件,根据引理3知,按照SPT规则得到最优排序;如果所有批的学习因子都相等,那么可以将每一批看做一个工件,Pi作为Bi的加工时间,那么问题1|B,LE,Tpart|ΣΣCij等价于问题1|LE|ΣCj,由引理3知按照Pi不减的顺序排列即可得最优排序.
3.3 批与批之间有总的学习效应的传递
不失一般性,我们假设Bi是在第i批加工,那么Bi中的工件Jij在第r个位置上加工时,其实际加工时间为,该问题可以用三参数表示法记为1|B,LE,Ttotal|ΣΣCij.
定理6 对1|B,LE,Ttotal|ΣΣCij问题,每一批内工件的总完工时间的SPT最优值可以按正常加工时间的规则排列得到.
证明 假设π为一最优排序,对于Bi中的两个工件Jij和Jil,满足pij≥pil,Jij在Bi中的第r个位置上加工,Jil在Bi中的第r+1个位置上加工.令s表示在Bi中第r-1个位置上加工工件的完工时间,A和B分别表示在Jij和Jjl之前和之后加工的工件的总完工时间.
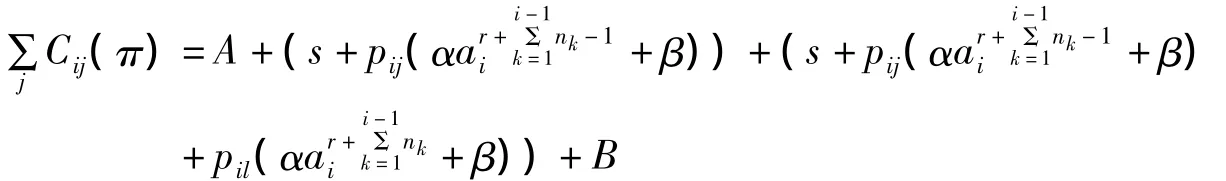
交换工件Jij和Jil的位置得到一个新的排序π',π'中交换Jij和Jjl的位置后,A不变.

由α≥0,β≥0,α+β=1,0<ai≤1知,所以有
这说明π'也是最优排序.对π中不满足SPT规则排序的工件进行调整,直到它们都满足SPT序为止,由此得到满足定理的最优排序.
推论4 对于问题1|B,LE,Ttotal|ΣΣCij存在一个最优排序使得每一批内的工件按正常加工时间的SPT规则排列.
下面我们讨论问题1|B,LE,Ttotal|ΣΣCij的一种特殊情况:
如果每一批内工件的个数都相等,即n1=n2=…=nm=¯n,记,则问题1|B,LE,Ttotal|ΣΣCij的批的加工次序问题可转化为下面的指派问题来求解:
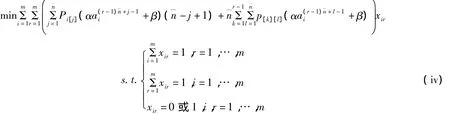
下面给出当n1=n2=…=nm=¯n时,求解问题1|B,LE,Ttotal|ΣΣCij的最优算法:
算法3.3 第1步 对于每一批内的工件,按正常加工时间的SPT规则排列;
第2步 根据指派问题(iv)来安排批的加工次序.
算法3.3的时间复杂性为O(n log n+m3).
定理7 当每一批内工件的个数都相等时,算法3.3能最优的解决问题1|B,LE,Ttotal|ΣΣCij.
[1]唐国春,张峰,罗守成,等.现代排序论[M].上海:上海出版社,2003.
[2]Biskup D.Single-machine schedulingwith learning considerations[J].European Journal of Operational Research,1999,(115):173-178.
[3]D.L.Yang,W.H.Kuo.A single-machine Scheduling problem with learning effects in intermittent batch production[J].Computer and Industrial Engineering,2009,(57):762-765.
[4]KuoW H,Yang D L.Minimizing themakespan in a single-machine scheduling problem with a time-based learning effect[J].Information Processing Letters,2006,(97):64-67.
[5]KuoW H,Yang D L.Minimizing the total completion time in a single-machine scheduling problem with a time-dependent learning effect[J].Eruopean Journal of Operational Research,2006,(174):1184-1190.
[6]王吉波,王明征.具有一般学习效应的单机排序问题[J].数学研究与评论,2005,25(4):642-646.
[7]Wang JB.Singlemachine scheduling with a time-dependent learning effect and deteriorating jobs[J].Journal of the Operational Research Society,2009,(57):9-16.
