二维有限元网格的局部调整及优化

2011-01-29江磊

制造业自动化 2011年4期

关键词：四边形加密编码

江磊

JIANG Lei

（成都纺织高等专科学校基础部，成都 611731）

1 网格的局部加密

1.1 局部网格加密算法的问题

在有限元网格加密中主要存在的问题[1]：多级加载和半带宽。对于单元局部加密的最大问题就是新增的单元、节点的编号如何处理，对于一般的有限元程序来说，如果单元和节点的变化不合理，对于生成的总体刚度矩阵的半带宽会加大，消耗更多的计算机内存。如坝体有限元计算程序，可模拟坝体修建的整个过程，模型是最终的坝体，然后记录了修建工程中的某些阶段，也就是多次加载。另外，为了能够适应现有的计算能力还必须合理的确定节点单元编码，这样可以减小半带宽。

1.2 算法具体描述

1.2.1 获得加密单元和过渡单元

有限元计算的结果通常经过后处理，我们在生成的等值线、彩色云图上很容易指定哪一部分的变化较剧烈，需要加密。用户使用鼠标选择加密区域，获得这个矩形的左上角和右下角的坐标：(left, top)，(right, bottom)。然后扫描所有的单元，只要单元的一个节点落在加密区域内，这个单元就是需要加密的。扫描结束后，生成一张表，记录需要加密的单元号。

1.2.2 产生新的节点

因为接触单元不可以划分为三角形单元，出现二角形单元有两种情况：(1)需加密的单元中含有三角形单元，在这种情况下，应为三角形单元不是接触单元，所以，划分不会产生三角形的接触单元。(2)在生成过渡单元这样的过渡单元时，如果过渡单元是接触单元的话，就产生了三角形的接触单元，这是不允许的，必须采取必要的措施。采取的方式是，如果某个加密单元的过渡单元是接触单元的话，则对应的这边就不增加节点，过渡单元也不进行划分。新增节点延续原来的节点编号，节点的坐标由所在的边或者所在单元型心确定。在这一过程中扩充原来的加密单元、过渡单元表格，使其包含需加密单元新增加的节点的信息。依次为边1增加的节点号，边2增加的节点号，边3增加的节点号，边4增加的节点号，型心处增加的节点编号。如果对应的部分没有增加节点，就写-1。

1.2.3 节点排序

要使生成的刚度矩阵具有合理的半带宽，需要单元和节点编码有一定的规律。通常网格在生成的时候都考虑了结构半带宽的优化，加密后的网格破坏了原有的半带宽。对于像坝体这样的矩形结构，可以先按照水平方向编码，然后竖直方向编码。把原来的节点信息表做一个备份。

1.2.4 单元排序

如何合理的对单元进行排序，是局部加密的关键。采用的是这样的一种想法：在加密前，如果一个单元的编码出现在另外一个单元的编码前，经过加密处理后，如果这个单元被拆分了，那么拆分后的几个单元的编码也要出现在另外的那个单元的前面。

2 网格质量优化

网格生成完毕后，其拓扑结构(如节点-单元关系、单元-单元关系、节点-节点关系)也就确定了，这些关系在一定程度上反映着网格的规则程度。通常，在四边形网格中任一个内部节点相连的最佳单元个数为4，但是任何一种生成四边形有限元网格的算法中，由于只考虑了节点周围局部的情况，而往往会在生成的网格中存在着不规则节点和由此导致的畸形单元。这些节点和单元的存在都直接影响着网格的质量，从而影响着有限元分析结果的准确性。

进行网格优化就是进一步提高网格质量以满足有限元分析的需要。总的来说，网格优化分为拓扑优化和几何优化两种。拓扑优化是改变网格的拓扑结构以达到优化的目的；而几何优化则不改变网格的拓扑结构，只是重新调整网格节点的位置，使单元尽量地接近正方形。本文采用网格优化算法，首先是通过改变网格的拓扑结构来使不规则单元的数量减少到最小，然后再对网格进行位置的优化，最终达到对整个网格质量的提高和改善。

2.1 拓扑优化

网格的拓扑优化[2]侧需要对网格节点之间的连接关系作出调整，对于四边形单元，节点连接的单元数介于3到6之间，认为是可以接受的。拓扑优化主要有以下几种模式：

删除节点；

删除单元；

删除边；

对角线调换；

在介绍网格的拓扑优化之前，先引进一个“度”的概念。在图论中，一个无向图中节点的度是指共享该节点的边的数目，这里重新定义为共享该节点的单元的数目：

2.1.1 点删除

这种拓扑优化主要应用于删除那些合并过程中四边形单元的内角有大于180o的单元的情况。依次检验内部节点，当某个节点的度为2时，必然会产生。

2.1.2 单元删除

依次检验所有的单元，如果此单元中存在一对相对的节点设为(A, B)度皆为3时，则删除此单元，并将节点A、B合并为一个节点。

2.1.3 边删除

依次检验连接了两个节点的单元边，如果某边AB的两个端点的度皆为3，则删除此边，连接到A、B节点的单元需要重新构建成两个新的四边形单元。这两个单元的公共边的选择需要按照节点的度来确定。设NC、ND、NF、NG分别为节点C、D、F、G的度，则两个四边形公共边的选择按如下原则：

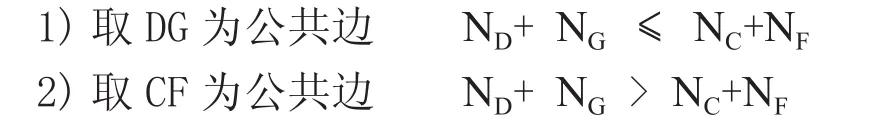
2.1.4 对角线调换

依次检验每一对相互连接的单元，公共边AD将被调换成EB或者CF，如果满足以下关系N1=NA+ND；N1= NA+ ND；N1= NA+ ND，则：

1)公共边AD调换成BE

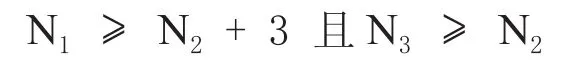
2)公共边AD调换成CF

需要注意的是：上面的拓扑优化执行的前提是这种调整不会引起任何的单元交叠或产生畸形单元。网格拓扑调整应该按照1-4的顺序进行。节点删除将首先执行，然后接着是单元删除、边删除和对角线的调换，当对角线调换完毕，再回到节点的删除，从而进行下一轮的拓扑调整，直到不需进行拓扑调整为止。

2.2 几何优化

网格的几何优化是指通过移动内部节点的位置来调整网格的形状以达到优化网格质量的目的。这类方法中最为典型的是Laplacian修匀方法，它用迭代法将每一个内部非固定节点移至由其邻接节点构成的多边形的形心位置，公式如下：

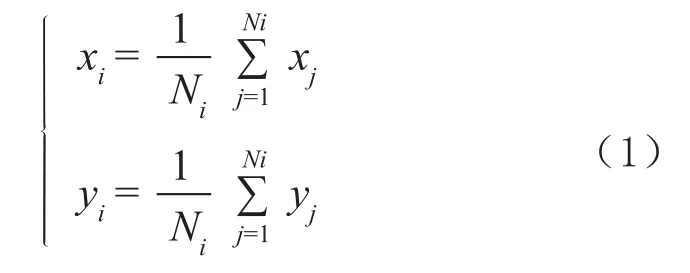
其中Ni是节点i所连接的节点总数，j是与i相连的节点，节点xi和yj是节点i的横坐标和纵坐标值。这种方法是通过移动内部节点位置的方法来优化网格单元的形状，同时使网格看起来更加光顺，所以也称其为一种网格的修匀或光顺的方法。

上式作为一个简单而又常常比较有效的迭代公式被广泛应用于网格修匀，但它也存在一些根本的缺陷：1)当存在非凸的几何区域时，某些单元可能会重叠，结点可能被移到区域的边界之外；2)在3D网格中，一个结点可能被移至某个相邻单元的内部；3)不能用于边界结点的调整。尽管后来Herrmann及其他研究人员又分别提出了一些改进的算法，但终究不可能克服修匀技术所固有的不足。

众所周知，在结构优化中优化方法可分为准则法和数学规划法两大类。数学规划法是严格按优化问题的数学描述进行求解，在理论上是严谨的，但在实际应用中其效率将随优化问题的规模增大而下降；准则法是基十直观推测，尽管有一定道理，但在理论上并不能保证获得最佳的结果。著名的三杆析架向题，己严格证明了满应力准则设计和最轻重量设计并不总是等价的。关于上述两类方法的实际应用，一般说来，设计变量少规模小的问题尽可能采用数学规划法来逼近最优解，而设计变量多规模人的问题尽可能引进准则的技巧来调整计算规模。

与此类似，在网格结点位置的优化中，Laplacian修匀属于准则法，它具有准则法普遍所具有的优点：方法简单，计算量小，速度快。Laplacian修匀技术作为网格生成方法的一种补充，己为大多数研究人员所接受。但是Laplacian修匀同样也具有准则法所固有的不足，最根本的问题在于不能确定修匀后的网格是否为最优网格。

图1为网格优化前后的比较。铺路法由于是从边界向区域内部生成单元，所以内部单元的质量比较差。从图中可以看出，经Laplacina修匀后，中心的网格质量得到提高。