基于SONS的结构模态参数识别研究

刘晓伟 李舜酩 张袁元

南京航空航天大学,南京,210016

基于SONS的结构模态参数识别研究

刘晓伟 李舜酩 张袁元

南京航空航天大学,南京,210016

仅利用结构的振动响应信号,提出了使用2阶非平稳源(SONS)盲分离方法识别结构模态参数的方法。在介绍SONS算法和采用盲源分离方法识别模态参数流程的基础上,以简支梁锤击振动响应信号进行了实验,并分析了响应信号含噪声的情况。实验表明,SONS方法准确地提取了简支梁结构的低阶模态振型、固有频率和阻尼比,抗噪性能好,且分离结果较二阶盲辨识(SOBI)算法准确、稳定。针对高阶模态直接盲分离识别效果不好的现象,采用先滤波再盲源分离的方法,成功识别了高阶模态固有频率。

响应信号;模态参数;盲源分离;锤击信号;信噪比

0 引言

盲源分离(blind source separation,BSS)仅从传感器观测信号中分离出源信号,具有其他分离方法无法比拟的优势,是一种很有应用前景的信号处理技术。自Jutten等[1]提出了一种类神经盲源分离,即现在常称的H-J算法以来,人们在盲源分离方面做了很多研究。近年来,在振动信号处理中应用盲源分离技术的文献越来越多[2],比如从复杂的混合信号中提取用于轴承诊断的信号[3]、从噪声环境中提取航空发动机转子振动信号[4]、内燃机振动信号的盲源分离[5]、混叠转子振动信号的盲源分离[6]等。

传统的线性模态分析是将位移矩阵分解为一个模态振型矩阵和一个模态坐标矩阵。模态坐标代表了结构基本的振动形式,模态振型则反映了系统响应中各个基本振动形式的参与量。时域模态参数的识别可以看做是一个盲源分离问题[2],混合矩阵提供了模态振型,盲源分离的信号则包含了各阶模态的固有频率和阻尼比信息。文献[2,7-8]讨论了应用 AMUSE(algorithm for mu ltip le unknow n signals ex traction)和二阶盲辨识(second order blind identification,SOBI)方法在系统的模态参数识别中的应用,指出了SOBI方法具有良好的抗噪性。文献[9]采用稳健的SOBI(R-SOBI)算法对四自由度的弹簧质量模型进行了分析,指出R-SOBI算法比SOBI算法具有更好的抗噪性。

本文采用二阶非平稳源(second order nonsteady source,SONS)盲分离方法对结构的振动响应信号进行信号分离,得到振型矩阵,然后通过从分离得到的单自由度信号中提取频率及阻尼比,从而得到结构的各阶模态参数。

1 盲源分离的基本概念

盲源分离是指在源信号与混合通道参数均未知的条件下,仅通过传感器观测信号来估计源信号的一种信号处理方法。盲源分离的数学模型可表示为

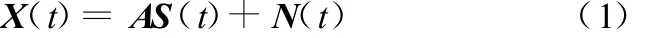
N个未知信号源Si(t)(i=1,2,…,N),构成一个列向量S(t)=(s1(t),s2(t),…,sN(t))T,t是离散时间。A是一个M ×N矩阵,称为混合矩阵。N(t)=(n1(t),n2(t),…,nM(t))T是 M 维观测高斯噪声信号。而 X(t)=(x1(t),x2(t),…,xM(t))T则是通过传感器观察到的M维向量,通常情况下,假设噪声是加性高斯噪声。含有噪声的盲源分离模型处理起来十分棘手,为简单计,通常的研究不考虑噪声的影响,其分离模型可表示为

式中,Y(t)为分离信号矢量(即源信号的一个估计值);W为N×M矩阵,称为分离矩阵或解混矩阵。

由于混合系统的参数和源信号的先验知识都是未知的,所以需要作如下假设:①各源信号之间相互统计独立,且源信号之间最多只有一个高斯分布的源,否则不能分离;②观测信号数大于或者等于源信号数,且混合矩阵为列满秩矩阵。

在上述假设条件下,盲源信号分离的求解结果有不确定性,主要表现为分离后信号矢量的排列顺序可以变化和信号的幅值与初始相位可以变化。但通常这并不影响源信号的识别,因为源信号的大多数有关信息都包含在其波形上,而不是在它们的幅值和排列次序上。

2 二阶非平稳源盲分离算法

在SOBI算法中,白化矩阵是通过零时延协方差矩阵的特征分解求得,这不能有效降低噪声的干扰,会影响算法的分离精度。SONS方法采用一种稳健的白化方法,即利用多个时延协方差矩阵生成一个线性混合矩阵,通过适当的参数选择来保证该线性组合矩阵的正定性,进而对该矩阵进行奇异值分解来获取相关的白化矩阵,并获取白化信号。该白化算法是一个迭代运算过程,对加性噪声的影响不再敏感。该方法按如下步骤来实现:

(1)计算观测数据在不同时延τj下的协方差矩阵 CX(τj),并调整为

SONS算法步骤可以归纳为:①利用上述的稳健白化算法对观测信号进行白化处理,得到白化信号Z(t);②将白化信号Z(t)划分为互不重叠的K个数据块,计算每个数据块在不同时延下的协方差矩阵Mz(tk,τj);③将在 ②中得到的时延协方差矩阵进行联合近似对角化,得到正交分离阵ˆU;④求取分离矩阵W=ˆUTQ。

从而可以得到源信号的估计:

3 模态参数识别基本概念

模态参数识别包括提取结构一系列的模态频率、模态阻尼和模态振型。在这些参数中,模态振型以数学向量的形式描述了系统在某一模态频率下的振动形式,它反映了系统振动从物理空间到模态空间的映射关系。

根据结构动力学理论,一个n自由度线性系统的自由振动方程为

模态参数识别的任务就是从结构的响应输出x(t)中提取振型矩阵φ和包含在模态响应Q(t)中的模态频率ωi及模态阻尼比ζi。从式(14)可以看到,时域的模态分析与盲源分离之间存在着一些相似之处,两者都是从混合信号中估计潜在的组成分量;两者都是仅仅利用结构系统的输出信息。模态响应Q(t)相当于源信号S的一种特例。盲源分离主要是从混合信号中估计分离矩阵W=A-1,而这其中正包含有模态振型矩阵的信息,即φ=A。结构的模态频率wi及模态阻尼比ζi可以从分离信号Q(t)中分析得到。盲源分离方法提取模态参数的流程图如图1所示。

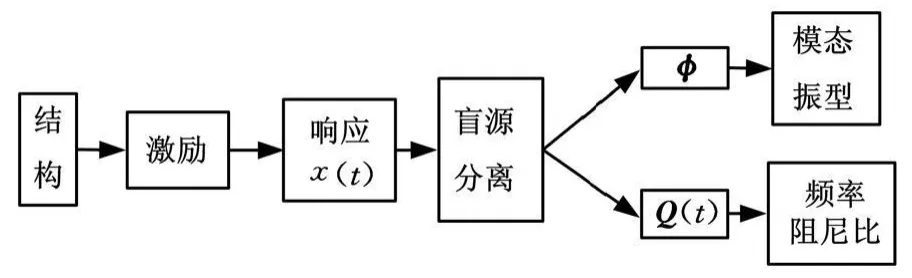
图1 盲源分离提取模态参数流程

4 实验研究

采用简支梁模型对盲源分离提取模态参数进行实验研究。简支梁的前3阶模态固有频率分别为 102.54H z、288.09H z、563、96H z,前 3 阶模态阻尼比为0.25%、1.45%、0.77%。对简支梁施加垂向锤击激励,用6个加速度传感器采集垂向响应信号,6个传感器的采样频率均为5000H z,响应信号如图2所示。

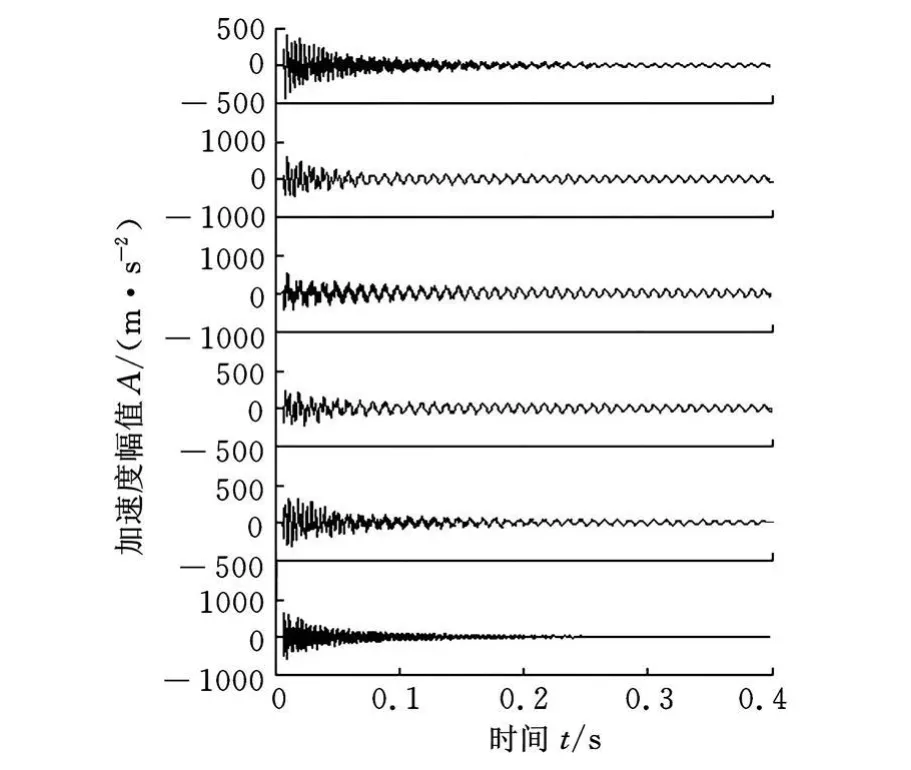
图2 简支梁锤击响应信号

采用SONS方法对振动响应信号进行盲源分离,得到的各个时域信号即为模态坐标下的单自由度振动响应信号,如图3所示。通过SONS算法所估计的各个分离信号的混合矩阵H就是模态振型矩阵,振型矩阵H的每一列都是一个振型向量,其阶次与分离信号相对应。混合矩阵H为

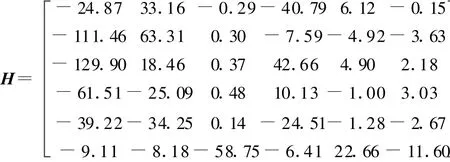
可以看出,通过盲源分离得到的振型矩阵能够反映前6阶振型的基本形状。对分离得到的时域信号进行频谱分析,就可以识别出各阶模态的固有频率,如图4所示。从图4可以看出,前3阶模态坐标响应信号得到了很好的分离,高阶模态坐标响应信号分离效果不好。

通过模态坐标下的单自由度响应信号,采用振幅对数衰减率的方法可以识别出各阶模态的阻尼比。简支梁前3阶模态固有频率、阻尼比识别结果见表1。表1中同时给出了SOBI(二阶盲辨识)算法和模态实验的结果。

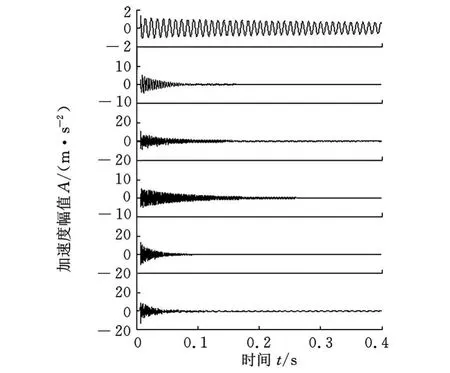
图3 SONS算法振动响应分离信号

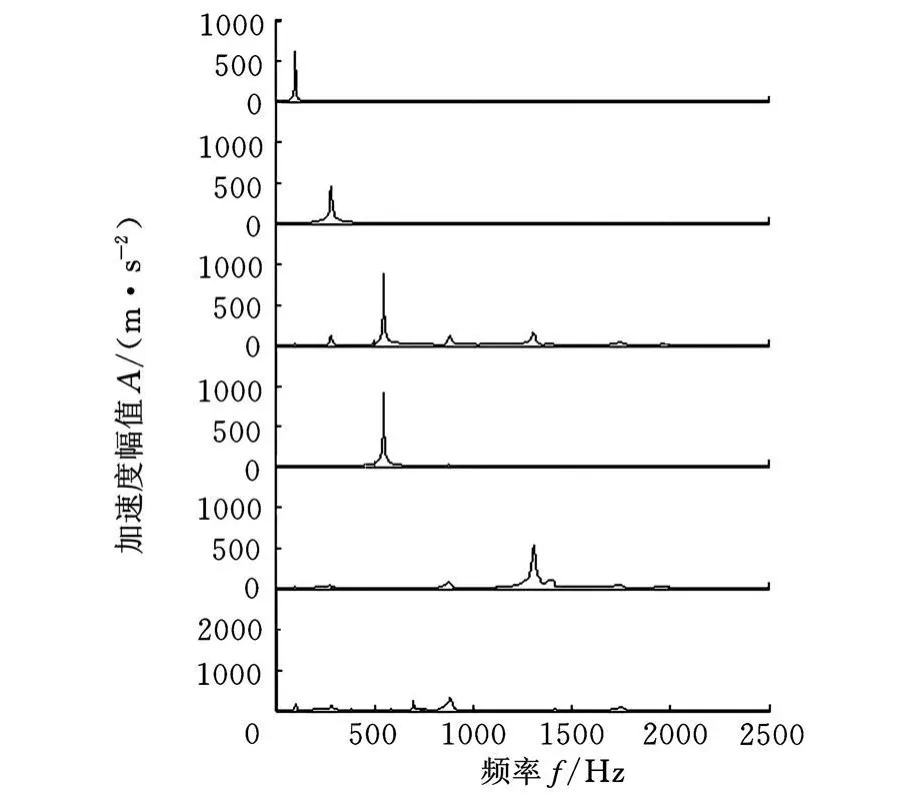
图4 SONS算法振动响应分离信号频谱

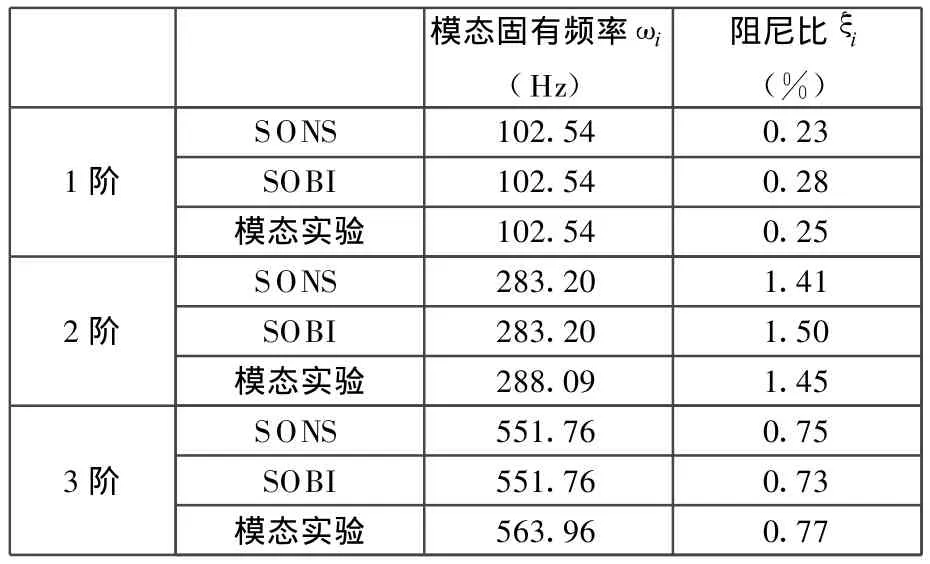
表1 盲源分离提取模态参数

从表1中可以看出,简支梁结构前3阶模态固有频率和阻尼比都得到了准确的识别,SONS算法和 SOBI算法的识别结果差别不大,但SONS算法比SOBI算法识别的阻尼比更加准确。对采集的锤击振动响应信号添加信噪比(SNR)为20dB的高斯白噪声,采用SONS算法进行盲源分离,分离结果如图5、图6所示。

从图5、图6可以看到,分离信号的顺序与未添加噪声时不同,这是由盲源分离本身的特性所决定的,不影响我们通过分离信号识别模态参数。

从图6可以看出,添加信噪比为20dB的高斯白噪声之后,结构前3阶的模态固有频率仍然可以得到很好的识别,通过分离的时域信号可以提取模态阻尼。进一步增加噪声强度,对锤击响应信号分别添加信噪比为15dB、10dB和5dB的高斯白噪声,进行盲源分离,并与SOBI分离结果进行对比,模态参数的识别结果见表2。

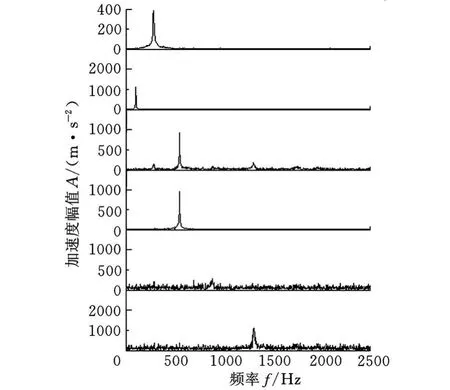
图6 信噪比为20dB时响应信号的SONS分离信号频谱

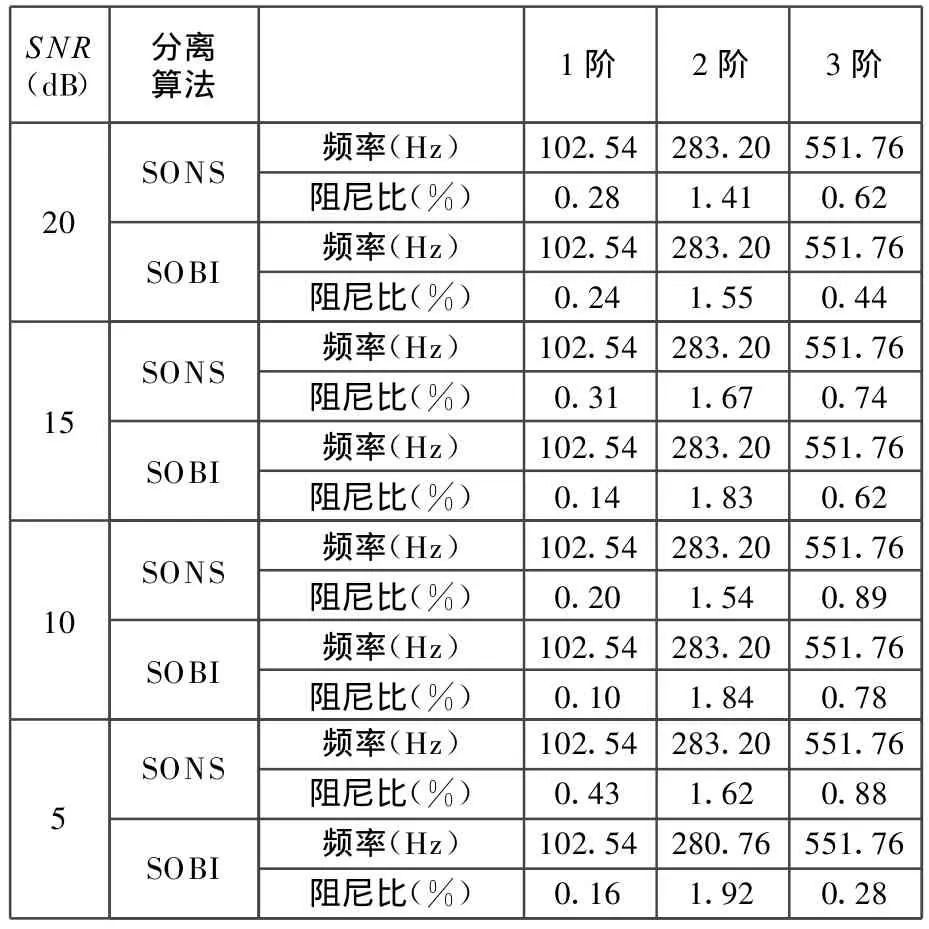
表2 不同信噪比下频率、阻尼比识别结果

从表2中可以看出,对于含噪声的信号,两种方法对模态固有频率的识别结果基本相同,但对阻尼比的识别,采用SONS方法的识别结果明显要优于SOBI方法的识别结果,特别是在信噪比为5dB的强噪声情况下。采用SOBI方法识别的阻尼比误差很大,并且识别结果不稳定,而采用SONS方法得到的结果较准确,且稳定性好,可见SONS算法比SOBI算法具有更强的抗噪性。

对于高阶的模态参数,由于分离出的时域信号受剩余模态的影响,阻尼比的识别受到限制,但模态固有频率可采用先滤波再分离的方法进行识别。从图 4可以看到,第4阶模态固有频率在886Hz左右,但其峰值较小,识别精度受到影响,因此可以滤掉800H z以下频率的信号,然后再采用盲源分离的方法分离信号。分离信号的频谱如图7所示。

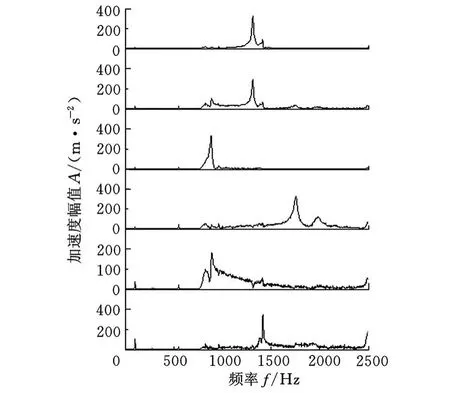
图7 滤波后SONS分离信号频谱

从图7中可以很明显地得到简支梁第4阶、第5阶和第6阶模态的固有频率,分别为883.79Hz、1311.04H z、1755.37Hz,通过模态实验得到的结果为 903.32H z、1346.26H z、1789.52Hz,可见通过先滤波再盲源分离的方法可以得到较准确的高阶模态固有频率。

5 结论

(1)直接采用SONS盲源分离算法就可以准确地识别振动结构的低阶模态参数。

(2)SONS盲源分离算法较SOBI盲源分离算法对模态参数的识别更准确。

(3)SONS算法具有很好的抗噪性,在强噪声环境下也能准确识别模态参数,且识别结果准确、稳定。

(4)对振动响应信号先滤波再进行盲源分离,可以准确识别高阶模态固有频率。

[1] Jutten C,Herault J.Blind Separation of Sources,Part I:an Adap tive A lgorithm Based on Neurom imetic A rchitecture[J].Signal Processing,1991,24:1-10.

[2] Zhou Wen liang,Chelidze D.Blind Source Separation Based Vibration Mode Identification[J].Mechanical System and Signal Processing,2007,21:3072-3087.[3] Zang C,Friswel M I,Im regun M.Structure Damage Detection Using Independent Component Analysis[J].Structure H ealth Monitoring,2004,3(1):69-83.

[4] 李舜酩.转子振动故障信号的盲分离[J].航空动力学报,2005,20(5):751-756.

[5] 石林锁,袁涛.内燃机振动信号的盲源分离方法试验研究[J].内燃机学报,2007,25(5):463-468.

[6] 雷衍斌,李舜酩,郝青青.一种基于累积量的盲源分离新方法及其应用[J].中国机械工程,2010,21(7):787-792.

[7] Kem chen G,Ponce let F,Golinval J C.Physical Interpretation of Independent Component Analysis in Structural Dynam ics[J].Mechanical System and Signal Processing,2007,21:1561-1575.

[8] Poncelet F,Ke-ehen G,Golinval JC,et al.Output Only Modal Analysis Using Blind Source Separation Techniques[J].Mechanical System and Signal Processing,2007,21:2335-2358.

[9] 付志超,程伟,徐成.基于R—SOBI的结构模态参数辨识方法[J].振动与冲击,2010,29(1):108-111.

A Study of Structure Modal Parameter Identification Based on Second Order Non-stationary Source Separation

Liu Xiaowei LiShunm ing Zhang Yuanyuan
Nanjing University o f Aeronautics&A stronautics,Nanjing,210016

A method of identifying the structure's m odal parameters by second order nonstationary source separation(SONS)arithm etic was proposed only using structure's vibration response signals.On the basis o f introducing the process of SONS algorithm and the steps of using BSSmethod to identify modal parameters,an experimentwas carried out using the hammering signals of sim ply supported beam,and the response signals w ith noise were analyzed.The experim ent demonstrates that the structure's low order mode shape,natural frequency and dam ping ratio are picked up by SONS method accurately.The SONS algorithm has good noise immunity,and its separation resu lts are better and more steady than SOBI(second order b lind identification)algorithm.Aiming at the phenomenon where high order modal parameters can not be identified very well using direct BSSmethod,amethod of doing BSS after signal filtering was proposed and high order natural frequency w as identified by thismethod successfully.

response signal;m odal parameter;blind source separation(BSS);hammering signal;signal-noise ratio(SNR)

TB123

1004—132X(2011)12—1454—05

2010—08—05

江苏省研究生培养创新工程资助项目(CX10B_094Z)

(编辑 何成根)

刘晓伟,男,1987年生。南京航空航天大学能源与动力学院硕士研究生。研究方向为信号处理、振动与噪声控制。李舜酩,男,1962年生。南京航空航天大学能源与动力学院教授、博士研究生导师。张袁元,男,1983年生。南京航空航天大学能源与动力学院博士研究生。