球面4R机构运动特性研究及其应用探索
2011-01-29周香琴
周香琴
浙江理工大学,杭州,310018
球面4R机构运动特性研究及其应用探索
周香琴
浙江理工大学,杭州,310018
为了运用球面4R机构满足周期性往复运动的需求,以GTM剑杆织机中球面4R引纬机构为研究对象,建立了机构的结构参数和输出运动参数之间的函数关系,利用数学方法得出了机构运动函数的特性,分析了各结构参数对运动曲线形态的影响。通过组合相关的结构参数,获得了不同形态的运动曲线,实现了机构的变异,扩展应用到引纬机构的扩幅设计和开口机构的创新设计中。研究结果表明,通过合理组合球面4R机构中的两个结构参数可以实现多种应用。
球面4R机构;运动特性;曲线形态;剑杆织机;引纬
0 引言
引纬机构是剑杆织机的核心机构,它决定了织机的车速。在高档的剑杆织机中,球面4R机构(用于引纬驱动)因其结构紧凑、运动副简单、加工安装方便、成本低并且适应高速工况而深受欢迎。RSSR机构、4R机构目前的研究大多为理论研究[1-5]。从工程实际要求出发,有针对性地研究运动特性,为工程应用提供理论依据的应用基础研究比较少见。笔者通过数学论证和数值计算相结合的方法,分析该机构的运动特性,建立相关机构参数与运动性能之间的映射关系,通过组合设计有关参数,达到机构创新的目的,扩大机构的应用领域,为灵活运用4R机构提供方法和思路。
1 GTM剑杆织机引纬机构介绍
GTM剑杆织机是比利时PICANOL公司于20世纪90年代生产的剑杆织机。图1所示为该机的引纬驱动机构。与主轴固连的旋转臂1通过滚针轴承与叉形连杆2连接,叉形连杆2与十字节3通过推力轴承连接,十字节通过轴承固定在箱体上。旋转臂1、叉形连杆2与十字节3上的所有运动副轴线交于一点C,形成一个球面4R机构,从而起到调节引纬动程的作用。十字节3和扇形齿轮5通过中心分别位于E点和F点的轴承与H形连杆4连接,扇形齿轮5通过中心位于G点的轴承与箱体连接,形成了一个平面四连杆机构,铰接点F在扇形齿轮的长槽上滑动,用以改变扇形齿轮的摆幅大小,起到调节引纬门幅的作用。扇形齿轮5与传剑轴6上的齿轮啮合 ,实现引纬动程的放大。传剑轴6通过固定在其上的剑轮,带动剑头和剑带运动,实现剑杆织机的引纬功能。

图1 GTM剑杆织机引纬驱动机构
图1a、图1b所示分别为GTM剑杆织机主轴处于180°(两剑头交接纬纱的位置)和0°时的位置,旋转臂1在正常织造时的转动方向为图1所示方向。由于有了一套平面四连杆机构,其中,扇形齿轮上用于调节F、G间距的长槽可以根据需要设计。在GTM剑杆织机中,当织机主轴处于180°时,E点处于引纬动程调节长槽的圆心上(图1a的位置),此时F点沿圆弧槽改变位置,扇形齿轮的位置不会改变,即剑头的位置不会改变,所以采用该方法调节剑头动程可以实现剑头交接纬纱时刻位置不变,操作简便。通过以上的分析,我们可以得到GTM剑杆织机引纬驱动机构简图(图2)。
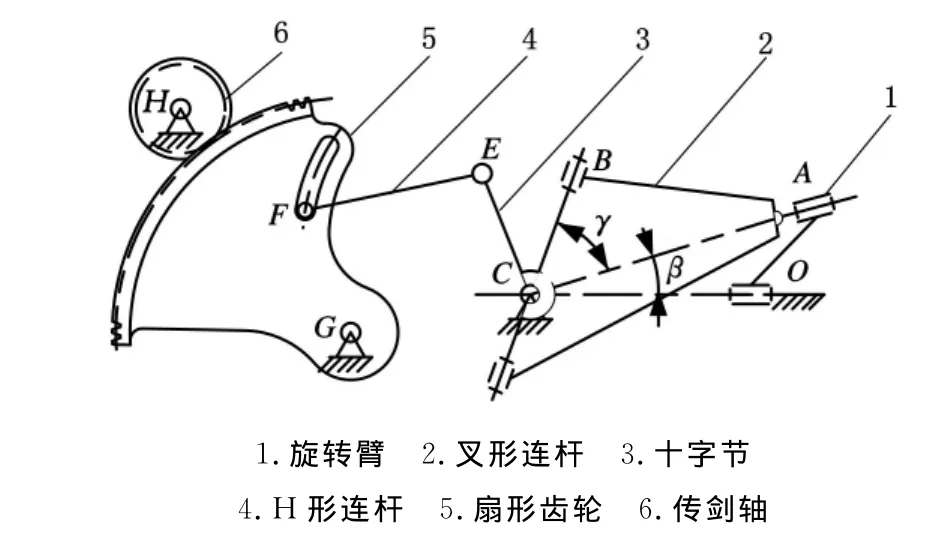
图2 GTM剑杆织机引纬驱动机构简图
2 球面4R机构运动函数的推导
由前面的分析可以看出,引纬运动的规律变化主要是由OABC球面的4R机构控制的,该机构的输入构件为旋转臂1,输出构件为十字节3,它们的运动方向正交。下面重点分析该机构的运动函数。
在旋转臂与叉形连杆的相对运动轴线AC上取一点A,在旋转臂的转动中心轴线OC上取一点O,使OA⊥OC,假设O、A两点的间距为L1,旋转臂上两运动副轴线OC与AC的夹角为β。在叉形连杆与十字节的相对运动轴线BC上取一点B,假设A、B两点的间距为L2,叉形连杆上两个运动副轴线AC与BC的夹角为γ。假设十字节上两点B、C的间距为L3,机架上两点O、C的间距为L4,A、C两点的间距为L5。以O点为坐标原点,OC所在的直线为X轴,CB的运动平面为OXY平面,建立如图3所示的直角坐标系。
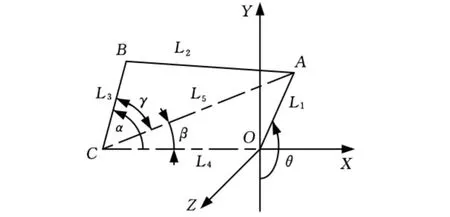
图3 球面4R机构结构参数示意图
θ为OA在OYZ平面内的转角。α为CB在OXY平面内的转角,θ与α的起始位置和正向如图3所示。
根据前面的分析可知:OA 在OYZ平面内绕X轴做圆周运动,BC在OXY平面内绕C点做摆动,AB绕C点做空间运动。

式(7)为球面4R引纬机构的运动函数方程,因为γ为叉形连杆的结构参数,β为旋转臂的结构参数,根据式(7)可以得到α=f(θ)的函数对应关系。在实际机构中,重点要研究的是f(θ)-f(0°)与结构参数γ和β之间的关系。现假设α1=η(θ)=f(θ)-f(0°)。

3 函数特性研究
3.1 函数的对称性和机构存在条件

3.2 函数的单调性
对式(7)求一阶导数并整理后得到

3.3 极值


3.4 γ=90°时的函数性质

3.5 γ=c与γ=180°-C时函数之间的关系

3.6 结构参数β、γ对函数形态的影响
在实际的GTM引纬驱动机构中,β=30°,γ=60°。剑头剑带的动程与十字节的初始角无关。前面的讨论中,θ以逆时针方向为正,但实际机构中,正常运转时θ以顺时针方向运转。由于η(θ)关于θ=0°对称,所以旋转臂1顺转和逆转的规律相同,前面的讨论能代表实际机构的运行情况。另假设ζ(θ)=f(θ)-f(180°)。

固定γ=60°,分别取β=10°,20°,30°,35°,40°,为了便于讨论运动曲线的形态,把不同β值对应的曲线通过一个系数M(β)修正,使函数的极值相同。假设ξ(θ)= M(β)η(θ),求得相应的ξ(θ)(θ)、(θ),得到图6所示的曲线规律。其中M(β)是一个只与结构参数β有关的系数。
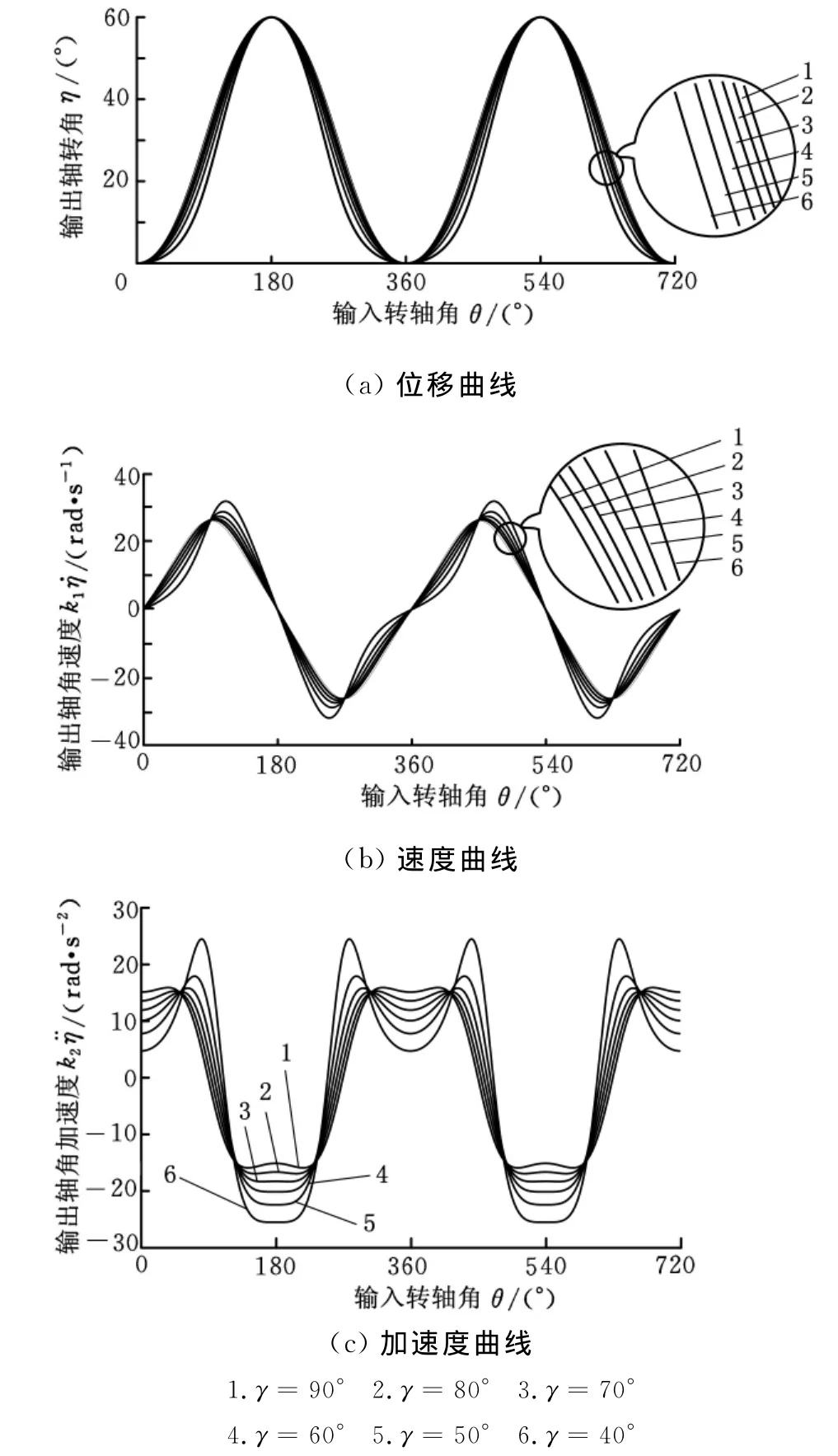
图4 γ对运动函数形态的影响(30°<γ≤90°)
3.7 讨论
通过上文的分析可知,随着γ的增大,加速度和速度的最大值减小,位移曲线在0°附近比较平缓,在180°附近相对陡一些。γ大于90°后,随着γ的增大,加速度和速度的最大值增大,位移曲线在180°附近比较平缓,在0°附近相对陡一些。ζ(θ+关于θ轴对称,与3.5节的结论一致。
从图4、图5可以看出,γ=90°时η加速度曲线比较平缓,速度曲线关于θ=90°,θ=270°对称,位移曲线在0°和180°附近平缓程度相同,与3.4的结论一致。
通过上文的分析,并从图6可知,随着β值的加大,最大加速度、最大速度值在加大,位移曲线在0°附近逐渐趋于平缓,在180°附近变化不明显。
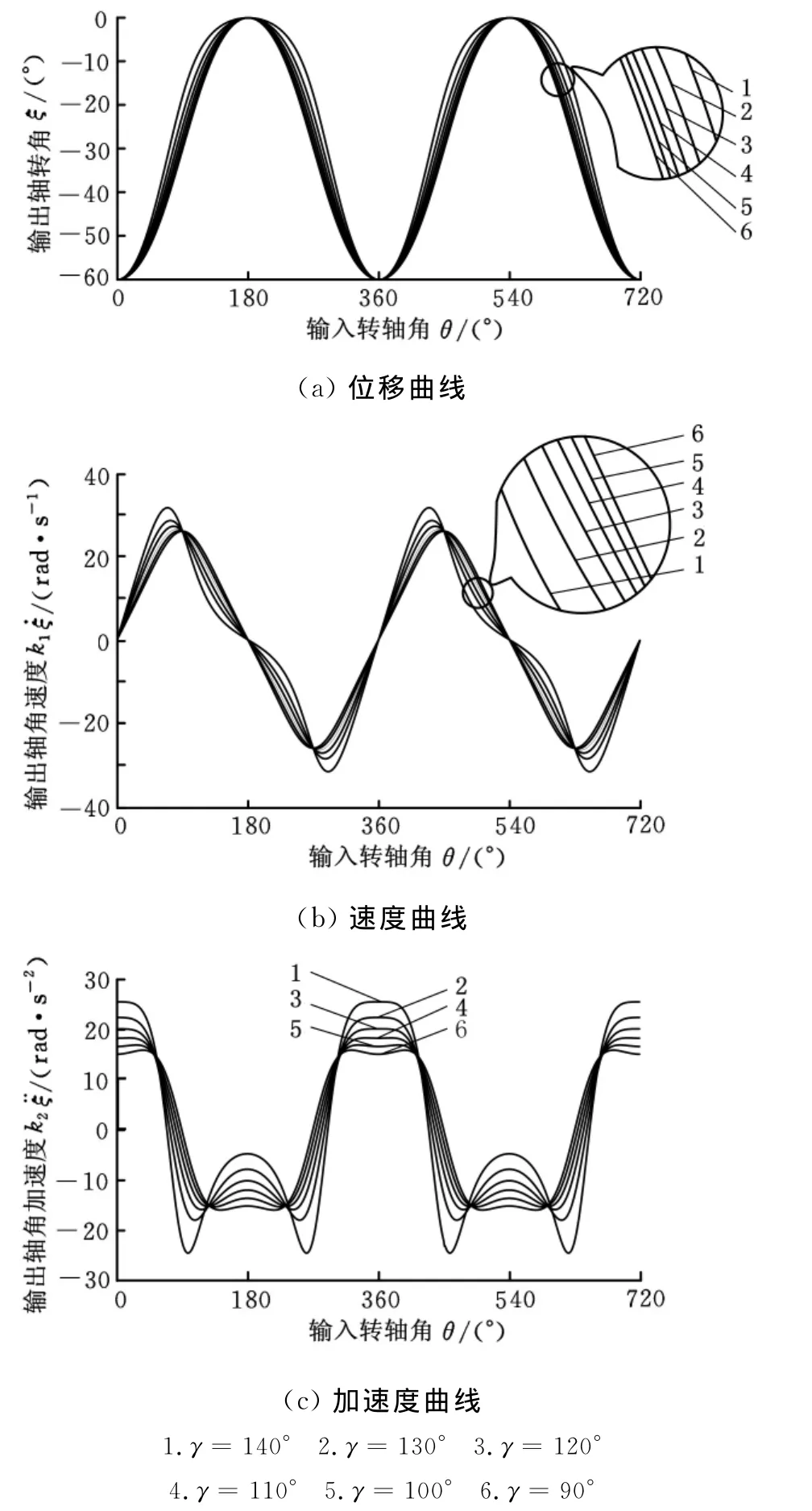
图5 γ对运动函数形态的影响(90°≤γ<150°)
4 应用探索
4.1 增加总动程减少空动程的应用
在实际的引纬机构设计中,剑头的运动规律需要与打纬和开口的运动规律相配合,剑头进入梭口的时间是有规定的,剑头在梭口外的动程一般称为空动程。在引纬机构的设计中,特别是在宽幅织机的设计中,控制空动程是一项重要的任务。空动程大,机器的占地面积大、刚性差;空动程小,引纬的最大速度、最大加速度大。在GTM剑杆织机中,引纬机构能适应的最大织机门幅是280cm。采用增大齿轮传动比的办法,可以达到增大引纬门幅的效果,但是空动程也按总动程的比例一起增大,若采用这种方法扩大门幅,整个引纬机构的结构更改大、成本高。根据前面的讨论分析可知,可以采用增大β、减小γ来达到增大总动程、减小空动程的效果,并且保证β+γ的值不变,保证机构的外形尺寸不变。为配合齿轮速比的适当变化,在保证强度的前提下,更换少量的零件,来满足引纬机构扩幅的要求,通过这种方法成功地将该引纬机构的适应门幅增加到360cm。

图6 β对运动函数形态的影响(0°<β≤90°)
4.2 运动曲线反向的应用
在剑杆织机中,引纬机构的外形尺寸和结构布局往往影响整台织机的结构。针对不同的门幅,为了较好地设计系列型剑杆织机,引纬驱动机构的结构点的位置和外形尺寸最好变化不大或者不变,不影响周边的部件和墙板的结构。4.1节的应用完全符合这个要求,但要想再扩大门幅到540cm或更大,一味地增大β、减小γ已经不能满足要求了,需要增加一级齿轮传动,但这带来了剑头剑带运动方向改变的问题。
通过前文的讨论分析,我们可以看出,在其他参数相同的情况下,可以通过改变γ和输入参数θ的起始位置改变位移曲线的形态,满足位移、速度、加速度规律曲线的反向要求。利用这种方法成功地完成了门幅为540cm的剑杆织机引纬驱动机构的设计,通过分析,可以继续扩幅,应用到门幅达1000cm的剑杆织机上。剑杆织机机构如图7所示,图7中的主轴处于180°时的位置。与图2中的机构相比,增加了过渡齿轮7和过渡齿轮轴8(分别与传剑轴6上的齿轮和扇形齿轮5啮合),十字节3和叉形连杆2的连接方式改变了,90°<γ<180°-β。但外形尺寸和主要结构点位置基本没变,实现了引纬驱动机构的扩幅设计。

图7 特宽幅引纬驱动机构原理图
4.3 在开口机构上的应用
根据前文的分析可知,γ=90°时的球面4R机构能符合复动式开口驱动的基本要求,织机中综框的运动平面与主轴的运动平面垂直,且主轴转两圈,综框来回运动一次。在一般的织机中,主轴到开口机构的运动传输是通过一级同步带实现的,通过一级锥齿轮实现运动方向和运动速度的改变,再通过凸轮或偏心轮机构实现综框的开口运动规律要求。运用前面讨论的空间连杆机构可以实现两个功能,即运动方向的转变和开口运动规律的产生。开口机构要求的速比变化可以在同步带传输时实现,这样就可以减少一级锥齿轮的传动,简化了结构,降低了成本。如图8所示,主动同步带轮1与主轴固定,通过同步带2带动被动同步带轮3运动,实现运动的远距离传递和速度的变化,旋转臂4与被动同步带轮固定,通过由旋转臂4、空间连杆5、开口刀片6和机架组成的球面4R机构实现运动的转向和开口运动规律的生成,开口刀片通过多臂连杆(连杆机构)带动综框,实现织机的开口。该机构的缺点是只能适用于平纹开口,比较适合窄幅,优点是该装置结构简单、运动副少、成本低,而且比较适于高速运动。
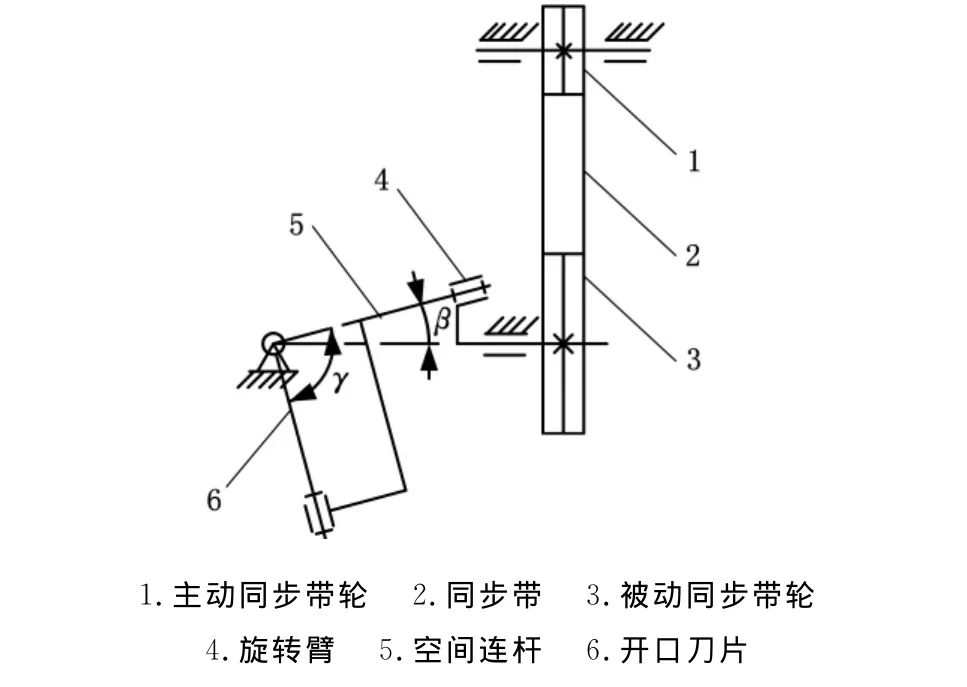
图8 简易开口机构驱动原理图
5 结束语
本文所讨论的球面4R机构,虽然只有2个结构参数γ和β,但通过选择合适的γ和β可产生不同的位移、速度、加速度曲线,来满足剑杆织机引纬空动程与总动程比值的不同要求。针对不同的目标函数如何选择最优的γ和β的匹配还有待进一步的研究。通过选择特殊的γ值,球面4R机构还能能应用到织机的开口部件中,作为开口驱动机构。
[1]陈建能,赵雄,徐宾,等.椭圆齿轮-曲柄摇杆引纬机构的运动学建模与特性分析[J].中国机械工程,2007,18(19):2294-2297.
[2]滕兵.织机引纬机构的分析研究[J].纺织机械,2008(5):46-48.
[3]苗鸿宾,乔峰丽.空间RSSR机构的运动分析和研究[J].机械设计与制造,2008(2):7-9.
[4]李克让,陈明.剑杆引纬机构的传动规律研究[J].纺织学报,2004,25(1):44-45.
[5]SommerⅢ H J.Jerk Analysis and Axode Geometry of Spatial Linkage[J].Journal of Mechanical Design,2008,130(4):042301.
[6]张启先.空间机构的分析与综合(上册)[M].北京:机械工业出版社,1984.
Kinematics Characteristics Research of Spherical 4R Mechanism and Its Application Explore
Zhou Xiangqin
Zhejiang Sci-Tech University,Hangzhou,310018
In order to apply spherical 4R mechanism to meet various reciprocating movements,based on spherical 4R weft insertion mechanism of GTM rapier loom,an output kinematics function of mechanism was established.Some important properties of kinematics function were proved with mathematic method,and the mapping between structure parameters and appearance of kinematics function curve was built.After creative design some structural parameters,some different appearances of kinematics function curve were obtained and the mechanism was changed.This changed mechanism can be used in designing weft mechanism and shed mechanism.The results indicate that many kind of applications can be obtained by reasonably combining two structure parameters in spherical 4R mechanism.
spherical 4R mechanism;kinematics characteristic;curve appearance;rapier loom;weft insertion
TH112.1
1004—132X(2011)02—0153—06
2010—04—09
国家科技支撑计划资助项目(2009BAF39B00);浙江省重点科技创新团队项目(2009R50018)
(编辑 张 洋)
周香琴,女,1965年生。浙江理工大学机械与自动控制学院高级工程师。研究方向为剑杆织机和机构学。发表论文9篇。
