各向异性双相介质弹性波场褶积算法数值模拟①

宫 猛，李信富

（中国地质大学（北京）地球物理与信息技术学院，北京 100083）

0 引言

双相弹性介质理论认为实际的地下介质是由固相、液相组成的。固相的多孔隙骨架是均匀的、各向同性的弹性固体；液相的充满孔隙空间的物质是具有粘弹性的、不可压缩的流体。特别是含油储层具有较大的孔隙度，表现出明显的双相介质性质。双相介质理论与单相介质理论不同，它充分地考虑了介质的结构、流体与气体的特殊性质、局部特性与整体效应的关系，因此更能准确地描述实际地层结构和地层性质，自然也就更能适应越来越复杂的油气储藏勘探的实际需要，从而引起了国内外地震学家和勘探地震学家们的高度重视，由此而发展起来的正演和反演研究具有更好的应用前景。1951年，Gassmann提出了关于弹性波在多孔介质中的传播理论［1］，并建立了著名的Gassmann方程（反映了速度与孔隙度之间的定量关系）。之后，Biot根据潮湿土壤的电位特性和声学中声波的吸收特性，发展了Gassmann的流体饱和多孔隙双相介质理论［2－3］，奠定了双相介质波动理论的基础。Biot理论充分考虑了孔隙介质的双相特性，发现了第二类纵波，并指出粘滞力控制孔隙流体的相对运动是弹性波在孔隙介质传播过程中发生衰减的重要机理，并于后人的工作中得到了验证、发展和应用。

由于Biot双相介质波动方程在复杂地质环境下没有确定的解析解，只能通过数值方法求得，所以人们对Biot双相介质的数值模拟做了大量研究。Zhu和McMechan用有限差分法模拟了双相介质［4］；Hassanzadeh用有限差分法模拟了双相介质中纵波的传播［5］；牛滨华等讨论了裂隙含流体、气体各向异性介质一维二、三分量波动方程［6］，然后用有限元方法进行了波场数值模拟；N.Dai等用一阶应力－速度波动方程模拟了各向异性双相介质［7］；牟永光基于Biot理论对双相PTL、双相EDA、及双相PTL十EDA介质中弹性波问题进行了深入研究［8］，给出了双相各向异性介质中弹性波方程的有限差分方法；邵秀民和蓝志凌推导了有人工边界时流体饱和多孔介质波动方程的有限元计算公式［9］；Arntsen和Carcione对双相介质中的慢纵波进行了模拟研究［10］；杨宽德等从同时包含两种力学机制的孔隙弹性波方程出发，利用有限差分法对含流体孔隙各向同性介质中的地震波和声波进行了数值模拟［11］，并与基于Biot流动的Biot理论之模拟结果进行比较；杨顶辉利用有限元方法对双相PTL介质和双相各向同性介质中的弹性波传播进行了数值模拟［12］；刘洋等推导了各向异性双相介质的伪谱法数值解法和有限元解法［13－14］；孙卫涛和杨慧珠采用交错网格技术建立了各向异性孔隙介质波动方程的高精度差分格式，并对这类差分格式的频散特性和稳定性作了详细分析讨论，解决了计算稳定性和边界反射问题［15］；王东等利用基于Biot理论的孔隙弹性介质的高阶交错网格有限差分算法，模拟了具有随机分布特征的多种流体饱和岩石中声波［16］；裴正林基于Biot理论给出了三维双相各向异性介质应力－速度弹性波方程交错网格任意偶数阶精度有限差分解法，对三维双相横向各向异性介质中弹性波场进行了模拟［17－18］。

双相各向异性介质是非常复杂的介质，也是目前地震学研究的前沿、热点课题和难点课题之一。双相各向异性理论是以双相各向同性理论和地震各向异性理论为基础，产生和发展的重要原因在于这种理论能够更真实地描述地下介质问题。Biot建立了孔隙各向异性介质理论，是研究双相各向异性问题的基础。

本文通过对李信富等提出的方法进行改进［19］，推出各向异性双相介质中地震波传播数值模拟计算的褶积微分算法，并对之进行数值计算检验。

1 双相介质波场模拟基本方程

Biot双相介质的运动平衡方程为

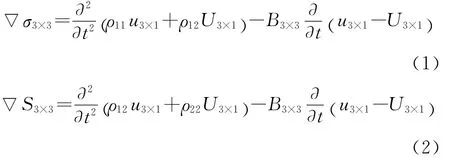
式中，ρ11，ρ12，ρ22为质量系数，ρ11表示单元体中固体相对流体运动时固体部分总的等效质量，ρ22为流体相对固体运动时流体部分总的等效质量，ρ12表示流体和固体之间的质量耦合系数，是粘滞、摩擦等效应的综合反映，又称为视质量。

为了得到一阶速度－应力方程，首先要将固相位移分量和流相位移分量从各自满足的方程分离开来。令式 （1）×ρ22－式（2）×ρ12，并整理得到固相位移分量公式：

令式 （1）×ρ12－式（2）×ρ11，并整理得到流相位移分量公式：

设固相速度矢量为v3×1＝ ［vx，vy，vz］，流相速度矢量为V3×1＝ ［Vx，Vy，Vz］，将速度对时间的一阶导数替换式（3）与式（4）中位移对时间的二阶导数，我们可以进一步得到固相速度和流相速度的一阶时间导数方程形式：

B3×3是耗散系数，对于各向同性Biot双相介质bx＝by＝bz；对于垂向横向各向同性Biot双相介质bx＝by。

进而，可以建立一阶速度－应力波动方程各分量形式如下：

固相速度分量

流相速度分量

固相应力分量

流相应力

2 双相介质波场模拟数值检验

为了检验本文方法的有效性，利用该方法对均匀横向各向同性双相介质和分层双相介质中弹性波场传播进行了数值模拟计算。

2.1 横向各向同性双相介质褶积算法波场特征

本模型考察横向各向同性双相介质中的地震波波场特征。网格点数为200×200；空间步长为10 m；时间步长为0.001s；介质方位角为零。震源位于模型中心位置，采用倾斜集中力源激发，Richer子波主频为15Hz，所用弹性参数如表1所示。图1是不同分量的波场快照。

从波场快照中可以看出，（1）在方位角为零的横向各向同性双相介质中，二维三分量数值模拟只能观测到三种波，即快纵波qP1、快横波qS1和慢纵波qP2，这三种波具有各向异性特性，且慢纵波属于第二类波，其余为的一类波。（2）由于不同方向上地震波的传播速度不同，地震波的波前面不再是圆形，而成为椭圆形，其曲率的大小由各向异性参数决定。（3）从波场快照中还可以看出，在二维三分量横向各向同性双相介质波场模拟中x分量和z分量的波场特征相似，y分量波场有所区别，y分量是由固体骨架各向异性引起的。

表1 均匀双相TIV介质物性参数

图1 横向各向同性双相介质模型弹性波场快照（介质倾角为0°；方位角为0°；t＝280ms）Fig.1 Snapshots of elastic wavefield in transverse homogeneous two－phase media（the dip is zero degree and the azimuths is zero degree.The propagation time of the wave is 280ms）.

2.2 两层横向各向同性双相介质波场模拟

本模型考察两层横向各向同性双相介质水平分界面上的的地震波波场特征。使用二维二分量格式进行模拟，介质方位角为零。模型如图2所示，网格点数为200×200；空间步长为10m；时间步长为0.001s；震源位于（100，60）处，采用倾斜集中力源激发，Richer子波频率为15Hz，主对称轴为z轴。分界面在z＝80处，接收排列在z＝50处，与界面平行。两层介质的弹性参数见表2。图3是各分量的波场快照。图3中可见，快纵波、慢纵波和快横波在界面上产生透射或反射后可以相互转换，其速度大小依次为：快纵波、快横波和慢纵波。由于各向异性介质中地震波传播的特殊性，只有在三维空间模拟才能全面认识波场的空间变化。

图2 两层水平分界面模型Fig.2 Two－layered model with a horizontal subsurface.

从图中可以看出：（1）双相TIV介质中的反射域弹性波有三类：直达类波：直达快纵波（qP1）、直达横波（qS1）、直达慢纵波（qP2）；反射波类：快纵波的反射波（qP1qP1）、横波的反射波（qS1qS1）、慢纵波的反射波（qP2qP2）；转换波类：由快纵波形成的转换横波（qP1qS1）、由快纵波形成的转换慢纵波（qP1qP2）、由慢纵波形成的转换快纵波（qP2qP1）和由横波形成的转换慢纵波（qS1qP2）。（2）从第一类波转换为第二类波后，该波型具有第二类波的性质；同样，从第二类波转换为第一类波后，该波型具有第一类波的性质。

表2 两层双相TIV介质物性参数

图3 两层双相TIV介质中弹性波场快照（介质倾角为0°；方位角为0°；t＝350ms）Fig.3 Snapshots of elastic wavefield in two－layered transverse homogeneous two－phase media（the dip is zero degree and the azimuths is zero degree.The propagation time of the wave is 350ms）.

3 结论与讨论

本文利用时间错格有限差分－空间褶积微分算子法来计算非均匀介质中的地震波场。时间错格有限差分－空间褶积微分算子法应用于地震波场数值模拟的主导思想是：利用基于Forsyte广义正交多项式褶积微分算子的有效表示计算波场对空间的偏导数，采用错格有限差分法计算对时间的偏导数，其计算思路类似于伪谱法。该方法是一种全新的、快速的、高精度的地震波场模拟方法，它相对于有限元法而言，可使用较大的网格；相对于有限差分法而言，频散效应小，计算精度高；相对于伪谱法而言，计算速度较快。

数值模拟结果表明，各向异性介质中波场数值模拟的褶积算法非常准确地模拟了各向异性介质中的波场传播过程，对各种波的刻画非常清楚，为研究复杂介质中地震波的传播特征提供了一种新的方法选择。

［1］Gassmann F.Elastic waves through a packing of spheres［J］.Geophysics，1951（16）：673－685.

［2］Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid. Ⅰ.low－frequency range［J］.J.Acoust.Soc.Am.，1956（28）：168－178.

［3］Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid.Ⅱ.higher－frequency range［J］.J.Acoust.Soc.Am.，1956（28）：179－191.

［4］Zhu X，G A McMechan.Numerical simulation of seismic responses of poroelastic reservoirs using Biot theory［J］.Geophysics，1991（56）：328－339.

［5］Hassanzadeh S.Acoustic modeling in fluid－saturated porous media［J］.Geophysics，1991（56）：424－435.

［6］牛滨华，吴有校，孙春岩.裂隙含流体气体各向异性介质波场数值模拟［J］.长春地质学院学报，1994，24（4）：454－460.

［7］N Dai，Vafidis A，Kanasewieh E R.Wave propagation in heterogeneous，porous media：A velocity－stress，finite difference method［J］.Geophysics，1995，60（2）：327－34.

［8］牟永光.储层地球物理学［M］.北京：石油工业出版社，1996：5.

［9］邵秀民，蓝志凌.流体饱和多孔介质波动方程的有限元解法［J］.地球物理学报，2000，43（2）：264－278.

［10］Arntsen B，Carcione J M.Numerical simulation of the Biot slow wave in water－saturated Nivelsteiner sandstone［J］.Geophysics，2001（66）：890－896.

［11］杨宽德，杨顶辉，王书强.基于Biot－Squirt方程的波场模拟［J］.地球物理学报，2002，45（6）：853－861.

［12］杨顶辉.双相各向异性介质中弹性波方程的有限元解法及波场模拟［J］.地球物理学报，2002，45（4）：575－583.

［13］刘洋，李承楚.双相各向异性介质中弹性波传播伪谱法数值模拟研究［J］.地震学报，2000，22（2）：132－138.

［14］刘洋，魏修成.双相各向异性介质中弹性波传播有限元方程及数值模拟［J］.地震学报，2003，25（2）：154－162.

［15］孙卫涛，杨慧珠.双相各向异性介质弹性波场有限差分正演模拟［J］.固体力学学报，2004，25（l）：21－28.

［16］王东，张海澜，王秀明.部分饱和孔隙岩石中声波传播数值研究［J］.地球物理学报，2006，49（2）：524－532.

［17］裴正林.二维双相各向异性介质弹性波方程交错网格高阶有限差分法模拟［J］.中国石油大学学报（自然科学版），2006，30（2）：16－20.

［18］裴正林.三维各向同性介质弹性波方程交错网格高阶有限差分法模拟［J］.石油物探，2006，41（2）：308－315.

［19］李信富，李小凡.地震波传播的褶积微分算子法数值模拟［J］.地球科学－中国地质大学学报，2008，33（6）：861－866.