第四方物流模式下库存与运输整合优化

姜 林

（重庆教育学院计算机科学系，重庆400067）

0 引言

库存控制与运输优化是两个重要研究领域，长期以来他们是分开研究的，随着供应链管理模式的出现，越来约多的企业为了获得核心竞争力而将物流作业外包给第三方物流，因此库存与运输整合优化问题（Inventory-Transportation Integrated Optimization，简称ITIO问题）应运而生。库存与运输整合优化问题的产生具有很强的现实意义，如何平衡二者之间的效益背反现象，已引起了管理界的广泛关注。Burns［1］（1985）研究了无限时间长度，单供方多需方的物品配送系统，并在直达运输和零担运输这两种策略下建立了EOQ模型。Federgruen［2］（1984）研究了客户需求随机、费用因素可变的ITIO非线性库存费用问题，建立了非线性混合整数规划模型，并用广义斑德分解算法来求解。DrorM.［3］（1987）建立了一个混合整数规划模型，通过引入惩罚和激励因子来反映相邻周期决策的相互影响，将长时间多周期问题简化为单周期短时间的配送问题。Mason［4］（2003）重点从信息角度研究减少装卸货的等待时间及减少处理费用的ITIO问题。Edwin-Romeijn.H.［5］（2007）针对双层供应网络结构，提出一种库存和运输联合优化的优化模型，并用嵌入遗传算法与分枝定界法求解。袁庆达［6］（2002）的博士论文中，针对战略层和其它层次的ITIO决策，构造了许多数学优化模型和求解算法。宋海清［7］（2008）考虑了多供应商通过配送中心向分销商供货的分销网络，并用拉格朗日方法求解。

目前的文献大多考虑配送过程中的库存与运输整合优化问题，如VMI模式下的库存-路径问题，鲜有文献引入第四方物流模式来考虑供应链分销系统的库存与运输整合优化问题。实际上分销系统的运输过程通常是由多个活动组成，比如先用汽车运输到港口，再报关，最后经水路运输到目的地等等，由于第三方物流代理商能力有限，不能独立完成众多运输任务中的所有活动，因此须将物流作业外包给第四方物流公司，第四方物流公司作为第三方物流的集成商，根据他们各自的优势将不同运输任务中的各个活动合理的分配给第三方物流代理商，在此过程中如果第三方物流代理商在实际条件允许下承担同一项运输任务的连续几个活动，或者是不同运输任务的相似几个活动，还可以减少成本，我们把前者称之为活动整合，后者称之为批量整合，这两个概念是由LeungLawrenceC［8］（2000）、LeungLawrenceC［9］（2009）提出来的，并已获得国际上的认可。活动整合减少的成本来自于代理商统筹安排、信息共享，批量整合减少的成本来自于代理商将运输任务合二为一，带来规模效应。本文的目标就是在这两种整合思想的引导下通过引入第四方物流模式建立起供应链分销系统的库存与运输整合优化的EOQ模型，并针对该模型设计相应的大规模邻域收索算法，使运输与库存费用最小。

1 问题的描述

我们考虑由一个供应商和L个客户构成的供应链分销系统，该系统中的运输任务由多个活动组成（如图1所示），供应商将整个物流作业外包给第四方物流公司，第四方物流公司合理的选择第三方物流代理商来完成运输任务中各个活动。我们假定供应商货品单一，客户无初始库存，需求量是确定的，并假定客户的需求量较大且地理位置分散，因此货物是直接运送的。｛Aj，j＝1，2，…，J｝表示完成所有运输任务的活动集合，特别的｛Aj，j∈φl⊆｛1，2，…，J｝｝表示完成第l项运输任务（第l项运输任务是指向第l个客户供货）所需活动，其中φ1表示完成运输任务l所需活动的指标集，例如φ2＝｛1，4，6｝表示完成第2项运输任务需要A1，A4，A6活动，｛Bi，i＝1，2，…，I｝表示可供选择的代理商集合。

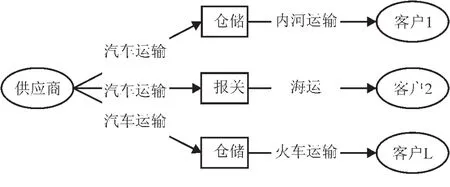
图1 模型示意图

∏＝｛π（i，l，τ），i＝1，2，…，I，l＝1，2，…，L，τ⊆φ1｝表示代理商在实际条件允许下可以承担的活动整合，其中π（i，l，τ）表示第i个代理商可以承担第l项运输任务的连续几个活动Aj，j∈τ⊆φ1，例如i＝3，l＝2，τ＝｛2，3｝表示第3个代理商可以承当第2项任务的A2，A3活动整合，在不引起混淆的情况下将π（i，τ，l）简记为π，特别的用∏l表示第l项运输任务中的活动整合，∏＝∏1∪∏2∪…∪∏L。

Θ＝｛θ（i，j，σ），i＝1，2，…，I，j＝1，2，…，J，σ⊆｛1，2，…，L｝｝表示代理商在实际条件允许下可以承担的批量整合，其中θ（i，j，σ）表示第i个代理商承担几个相似运输任务l，l∈σ⊆｛1，2，…，L｝的Aj活动，例如，i＝2，j＝3，σ＝｛4，5｝表示第2个代理商承担第4项和第5项运输任务的A3活动，在不引起混淆的情况下将θ（i，j，σ）简记为θ，特别的用Θ1表示含有运输任务l中活动的批量整合，Θ＝Θ1∪Θ2∪…∪ΘL。

2 模型的建立

我们用μl表示客户l的单位时间需求量，Cl表示客户l的最大库存容量，表示从供应商到客户l的最大发送频率，hl表示客户l单位时间单位货物的库存成本（不考虑供应商的库存成本），cijl表示第i个代理商承担第l项运输任务的Aj，j∈φl活动的成本，Ql表示客户l的每次运输量，fl表示客户l的发送频率，fl＝μl/Ql，w表示承当活动整合π获得的成本折扣，r表示承当批量整合θ获得的成本折扣，Wl表示承当活动整合∏l获得的成本折扣，Rl表示承当批量整合Θl获得的成本折扣分摊到任务l上的折扣，Wl的计算由定义即可得出，现举列说明Rl的计算，例如Θ2＝｛θ（2，1，｛1，2｝），θ（3，2，｛2，3｝｝，第2个代理商承担相似任务1和2的第1个活动以及第3个代理商承担相似任务2和3的第2个活动获得的成本折扣分别为30和24，对θ（2，1，｛1，2｝）而言，因为批量整合整合的是相似活动，所以进行第2项任务的第1活动平均分摊到的折扣为（1/2）×30＝15，同理进行第2项任务第2活动平均分摊到的折扣为（1/2）×24＝12，所以R2＝15+12＝27。特别的如果某一活动即属于一个活动整合又属于一个批量整合，那么我们不再重复计算成本折扣，也就是不再考虑该活动的批量整合成本折扣。

xijl表示第i个代理商是否承担第l项任务的Aj，j∈φl活动，xijl＝1表示承担，xijl＝0表示不承担，x＝（xijl，i＝1，2，…，I，j∈φl，l＝1，2，…，L）。

我们的模型目标是使长期平均库存与运输成本之和最小，模型建立如下1）目标函数

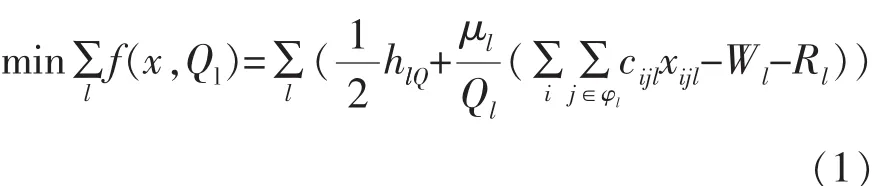
2）运输量Ql满足约束

3）每一项运输任务的每一个活动只能由一个代理商承担

4）由于代理商自身的资源有限，同时也为了保证任务完成的质量，每个代理商i承担的活动数目不超过ai

3 模型具有的性质

性质1：很容易看出f（x，Ql）是关于C（l）的单调函数。

证明：由函数f（x，Ql）在Ql∈［μl/f*l，Cl］上的单调性立即得出。

4 算法设计

该模型属于复杂的组合优化问题，其计算量呈指数型增长，在有限的时间内寻求精确解是不现实的，因此我们设计适合该问题的大规模邻域收索算法。大规模邻域收索算法作为一种启发式算法，其效率取决于初始点的选取以及邻域的结构，在我们的算法设计中采用一种快速有效的启发式算法来获得合理的初始解，同时在初始解的改进过程中，我们用活动交换改进图来设计邻域结构。

4.1 初始解的确定

从性质2看出运输费用的改变导致运输量和总成本的改变，过高的运输费用是由资源没有合理配置造成的，也造成了总成本的增加，是不经济的。我们基于优化运输过程中各活动的指派将导致合理的总成本的思想来确定初始解，另一方面在优化各活动的指派中，由活动整合与批量整合所获得的成本折扣相对于完成任务的成本来说是少量，因此在确定初始解时暂不考虑活动整合与批量整合，这样问题演变成一个广义指派问题，我们采用的算法的思想是首先指派哪些如果不将任务指派给成本最低的代理商将导致成本增加的任务。

Ijl表示尚未指派的第l项任务的Aj，j∈φl活动的集合，Mijl表示有能力接受第l项任务的Aj，j∈φl活动的代理商i的集合。对Aj∈Ijl，i1和i2分别表示承担成本最小和次小的两个代理商，Dj表示前面两种成本的差。

算法1：

步骤一 对所有的Aj∈Ijl，j∈φl计算Mijl，i1，i2，Dj；步骤二 选择j*使得Dj*＝max｛Dj｝；

步骤三 指派任务Aj*给对应的代理商i*1，更新参数，转步骤一。

4.2 初始解的改进

相对成本

改变活动的指派方案导致运输与库存费用总成

活动交换改进图

称有向图G＝（V，V′，E）为活动交换改进图，如果满足：①顶点V对应于所有的活动Aj，j＝1，2，…，J；②顶点V′是顶点V的复制；③E为有向弧（e，f′）∪（f′，g）的集合，e，g∈V，f′∈V′，弧（e，f′）表示活动e与f的交换，弧（f′，g）表示活动g将会是下一步交换的第一个活动，例如，图G中一条有3个弧（e，f′），（f′，g），（g，m′）的路径表示互换活动e与f，g与m的2步交换操作；④弧（e，f′）的边长c（e，f′）表示互换活动e与f的相对成本，弧（f′，g）的边长c（f′，g）为0。

通过活动交换改进图的定义我们可以看到改进图中的一条路径唯一地对应一系列活动交换，路径的长度对应交换后总成本的增量，初始解的改进就等价于寻找一条负成本增量的路径，幸运的是我们可以用最短路径算法来寻找一条成本减少最多的路径，从而找到最好的改进解。

随机搜索改进

如果xijl＝1，称xijl是基变量，称所有基变量的组合为一组基。随机搜索改进如下：首先随机选择一可行的活动整合将其放入基中，同时与之矛盾的变量xijl（不满足约束（3））设置为0，计算相对成本，如果相对成本小于0接受当前解为改进解，否则不接受，重复M次；其次对批量整合进行相似操作，重复N次。

5 算法步骤

算法总的流程框架如图2所示。

6 算例

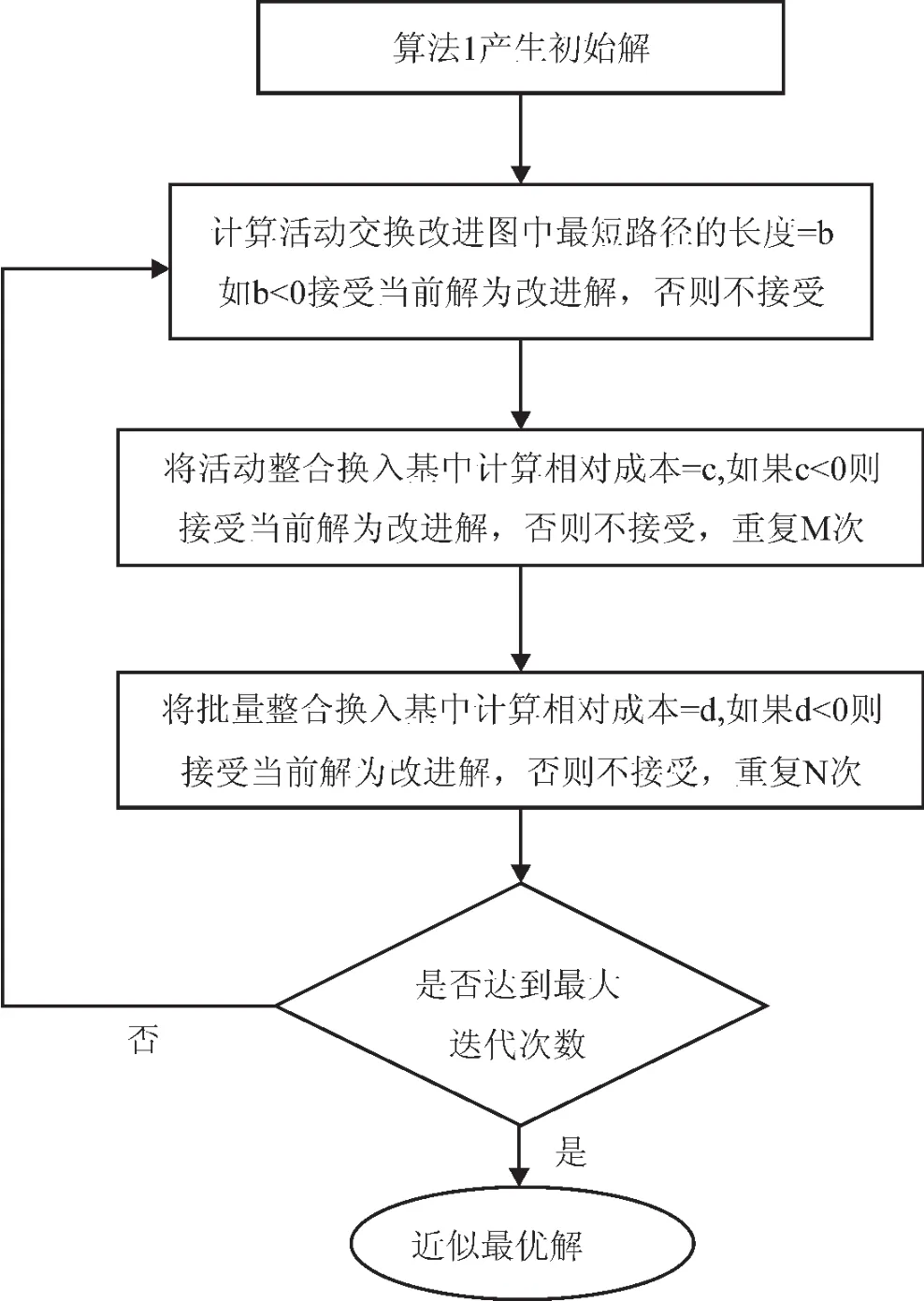
图2 算法流程图

我们假定供应商向3个客户供应货物，且向每一个客户供货的运输过程分为3个活动，每一个活动有3个代理商可以选择，成本如表1－2所示，库存费用h1＝10，h2＝11，h3＝11，单位时间需求量μ1＝7，μ2＝12，μ3＝20，最大库存容量C1＝15，C2＝20，C3＝25，最大发送频率＝2，＝3＝5，每个代理商最多承担5个活动。

由算法1产生指派方案：完成任务1活动1到任务3活动3的最小成本与次小成本差分别为1，4，3，3，2，2，1，11，1，其中最大值为11，对应将任务3的活动2指派给代理商2，则x223＝1，同理x321＝1，x331＝1，x112＝1，x222＝1，x232＝1，x211＝1，x113＝1，x133＝1，其它xijl为0，产生的活动整合｛π（3，1，｛2，3｝｝和｛π（2，2，｛2，3｝｝，产生的批量整合｛θ（1，1，｛2，3｝｝。由性质2有Q1＝9.1，Q2＝12.5，Q3＝19.3，总成本为450.7。

用Matlab7.0编程运算得到的活动交换改进图最短路：代理商3替代代理商2承担任务1的活动1，代理商1替代代理商2承担任务2的活动2与活动3，产生的活动整合｛π（3，1，｛1，2，3｝｝和｛π（1，2，｛1，2，3｝｝，产生的批量整合｛θ（1，1，｛2，3｝｝。由性质2有Q1＝8.8，Q2＝12.5，Q3＝19.3，总成本447.0。随机搜索不能改进解。

7 小结

本文在库存与运输整合优化的模型中引入第四方物流以及活动整合、批量整合的概念，并设计了适合该问题的大规模邻域搜索算法，得到了近似最优解，性能更好的算法和分析是值得继续研究的问题。

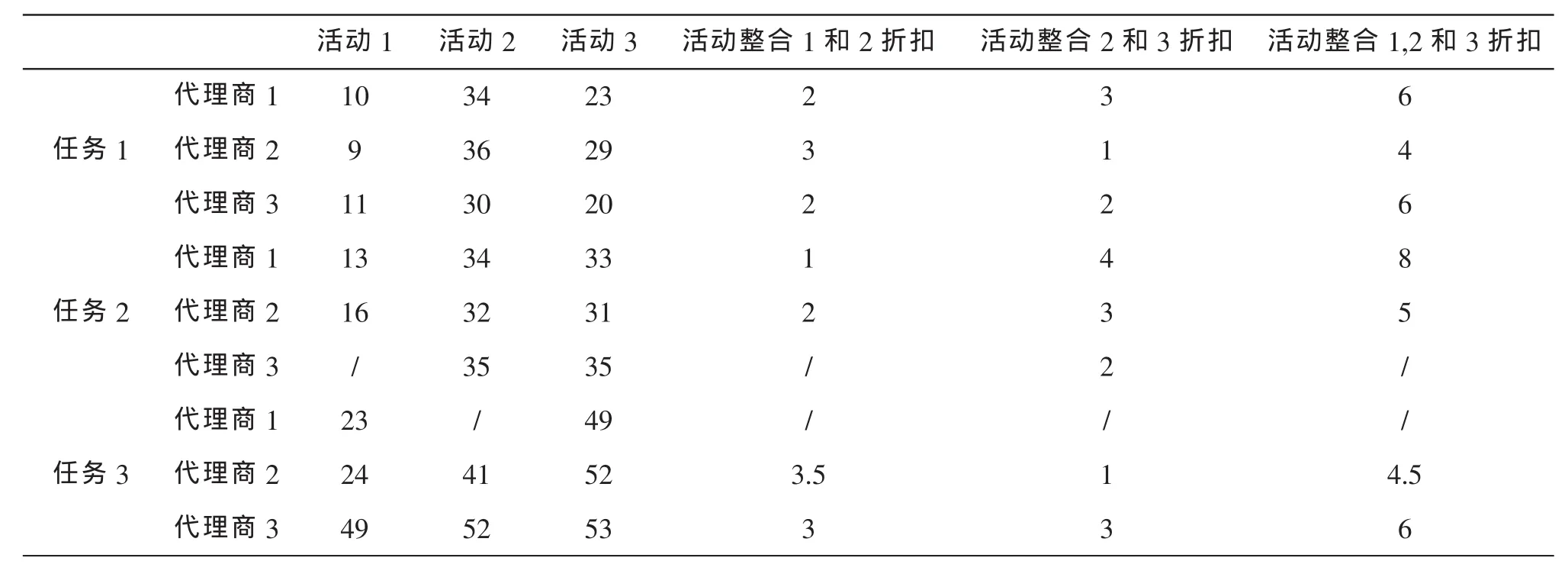
表1 承担活动成本以及活动整合成本折扣

表2 批量整合成本折扣表

［1］Burns L.D.，Hall R.W.Distribution strategies minimize transportation and inventory costs［J］.Operations Research.，1985，33（2）：469－490.

［2］Federgruen A.，Zipkin.A combined vehicle routing and inventory allocation problem［J］.Operation Research，1984，32（5）：1019～1037.

［3］DrorM.，BallM.Inventory/routing：reduction from an annual to a short－period problem［J］.Naval Research Logistics，1987，34：891－905.

［4］Mason S J..Integrating the warehousing and transportation functions of the supply chain［J］.Transportation Research，2003，39E：141～159.

［5］Edwin Romeijn.H.，Jia Shu and Chung－Piaw Teo.Designing two－echelon supply networks.European Journal of Operational Research，2007，16：449－462.

［6］袁庆达.随机型库存－运输联合优化问题的研究［D］.西南交通大学博士学位论文，2002.

［7］Haiqing Song，Vernon N.Hsu，Raymond K.Cheung.Distribution Coordination Between Suppliers and Customers with a Consolidation Center［J］.Operations Research，2008，56（5）：1264–1277.

［8］Leung，L.C.；Waiman Cheung；Yer Van Hai.A Framework for a Logistics E－Commerce Community Network：The Hong Kong Air Cargo Industry［J］.IEEE Transactions on SMC，2000，30（4）：446－455.

［9］Lawrence C.Leung，Yer Van Hui，Yong Wang.A 0–1 LP Model for the Integration and Consolidation of Air Cargo Shipments［J］.Operation Research，2009，57（2）：402～412.