Computing Models and Algorithms for Complex Co-design Systems

YE Hua and WU Ji-gang

(School of Computer Science and Software, Tianjin Polytechnic University Xiqing Tianjin 300387)

Computing Models and Algorithms for Complex Co-design Systems

YE Hua and WU Ji-gang

(School of Computer Science and Software, Tianjin Polytechnic University Xiqing Tianjin 300387)

Hardware/software (HW/SW) partitioning is a critical step in the design of complex embedded system. The computing models and the corresponding algorithms for hardware/software partitioning reported in recent years are summarized. The HW/SW partitioning is modeled as a variety of knapsack problems with different constraints, where items in knapsack problems correspond to the blocks in partitioning problems, and the communication cost between blocks is considered. Both exact algorithms and heuristic ones are introduced based on different computing models. Some potential problems on research are listed for future work.

algorithm; complex system; computing model; hardware/software partitioning

An embedded system is a system that has embedded software and computer-hardware, which makes it a system dedicated for an application or specific part of an application, product or a part of a larger system. Embedded systems typically consist of application-specific hardware parts such as FPGAs or ASICs, and programmable parts such as processors like DSPs or ASIPs. In comparison with the hardware parts, the software parts are much easier and faster to develop and modify. Hardware, however, provides better performance. For this reason, a system designer's goal is a system that minimizes the weighted sum of the software delay, hardware area, and power consumption. The weights are determined by the user according to the design preferences. Hardware/software (HW/SW) co-design which has become one of the primary applications of electronic system level tools and methodologies is used to make hardware and software work together to process the input as quickly as they can. A critical issue in complex embedded system co-design is to quickly find effective hardware and software partitioning with good complexity and performance estimations. The HW/SW partitioning must satisfy power, delay, and area measures while addressing salient factors such as the communication cost and the inherent overhead in the management of hardware resource.

There are many different academic approaches to solve the HW/SW partitioning. The traditional heuristics include hardware-oriented and software-oriented approaches. The hardware-oriented approach starts with a complete hardware solution anditeratively moves parts of the system to the software as long as the performance constraints are fulfilled[1-3],while the software-oriented approach starts with a software program moving pieces to hardware to improve speed until the performance of the final system meets the given constraint[4-6]. It has been shown that the HW/SW partitioning is NP-hard for most cases. Thus, many approaches for HW/SW partitioning emphasize on the algorithmic aspects proposed in recent years, e.g., simulated annealing algorithm[4,7-8], integer programming approaches[9-10],and dynamic programming algorithm[11-12]. All these algorithms can work perfectly within their own co-design environments, but it is impossible to compare them, because of the big differences in their co-design environments and the lack of benchmarks[13].

The related architecture for HW/SW partitioning is generally assumed to consist of single software and single hardware unit[11,14-19]. The system to be partitioned is given in the form of a task graph or a set of task graphs generally.

There are many models and algorithms for HW/SW partitioning reported in recent years. This paper can be considered as an up-to-date supplement,reporting the most recent developments in the HW/SW partitioning. The main objective of the paper is to provide readers with an overview of the area, in the context of a vision for models and algorithms on HW/SW partitioning.

1 Computing Models and Algorithms

Hardware/software partitioning decides which blocks of the system could be implemented in hardware and which ones could be realized as software.Hardware/software partitioning algorithm could be considered the standard knapsack problem proposed in Ref. [20]. The application of the embedded system is considered to be broken down into blocks such that each of them can be run simultaneously. So a set of items S = { p1,p2,,pn} is partitioned into hardware and software. The symbols of hiand sidenote the time required for the block pito be run in hardware and software, respectively. The symbol of aidenotes

1.1 Knapsack Model and Algorithm

the area required for hardware implementation of blockpi, and the symbolAdenotes the total area available for hardware implementation. A vector X= [x1,x2,,xn]such that xi∈ {0,1} used to denote the part piis implemented in software or hardware. The total running time of the application is given by:

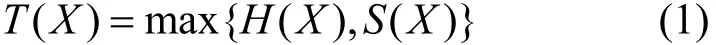
where H(X) is the total running time of the blocks running in hardware and S(X) is the total running time of the blocks in software. All the blocks that are realized in hardware can be run parallelly and all the software blocks are considered to be run serially. So the formula (2) is got:

The outline of the algorithm, denoted as Alg_HSP,for dealing with the hardware/software partitioning problem, is given below:

The proposed algorithm was simulated for different problem sizes and area constraints.Experimental results show that the large number of subproblems, which do not contribute to optimal solutions, could be eliminated rapidly by examining the upper and lower bounds of the subproblems. The proposed knapsack model does not include the communication overheads, so the model would be extended.

1.2 Area-efficient algorithm

HW/SW partitioning is a problem of improving the area utilization, reducing power and accelerating the execution of the embedded systems. Area efficiency is one of the major considerations in constraint aware HW/SW partitioning process. An efficient heuristic algorithm with the objective of minimizing area utilization under the constraints of execution time and power consumption is proposed in Ref.[21].

The efficient heuristic algorithm proposed is based on the partitioning model employed[11]. Fig. 1 shows the corresponding computational model for HW/SW partitioning.

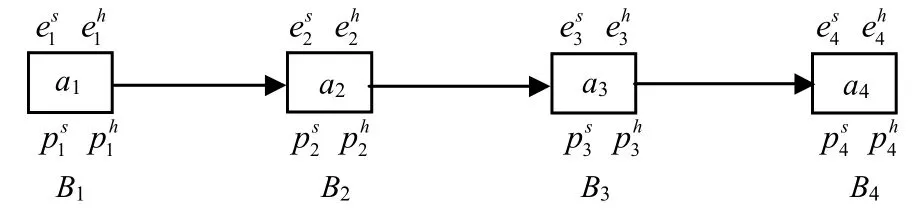
Fig.1 The system model used by the partitioning algorithms

The given application of the system corresponds to a sequence of n blocks, denoted as B1,B2,,Bn,that may be moved between hardware and software.The blocks may be functions or procedures, in which the communication between the blocks can be omitted.In order to yield the minimal area penalty while having an execution time less than or equal to the given constraintand having a total power consumption less than or equal to the given constraint, the formulation (5) is got.

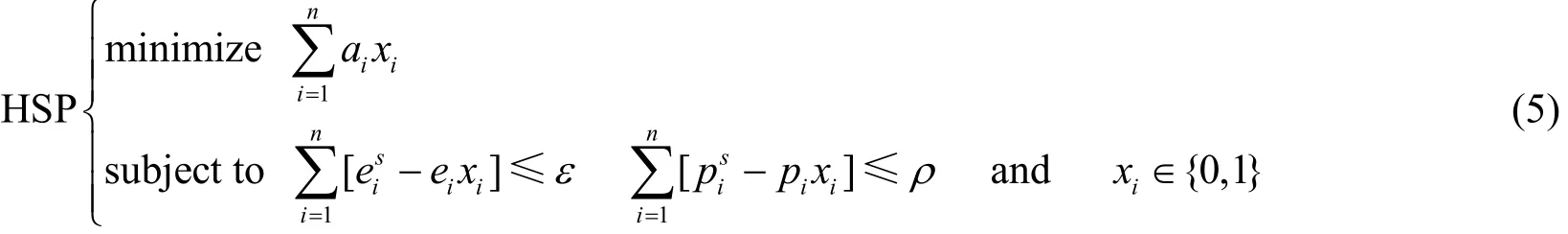
The following notations are used in the formulation (5)

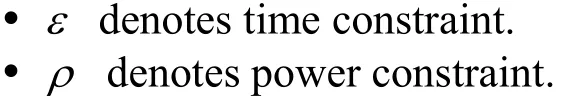
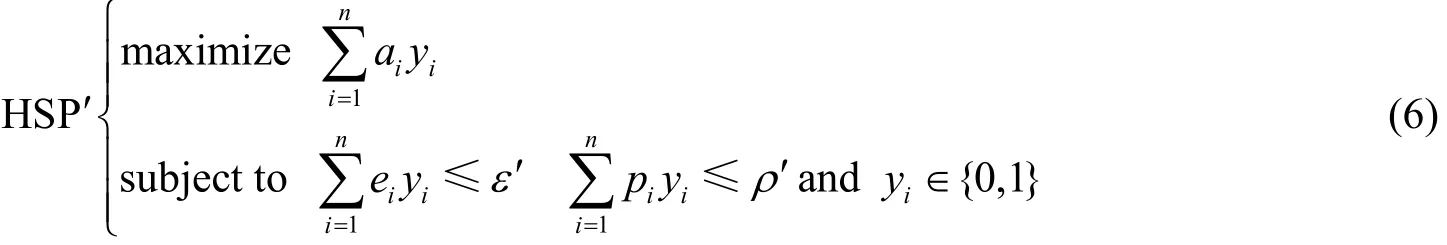
The problem HSP′ is an extended 0-1 knapsack problem, which is one of the most well-know NP-complete problems.

Then, the proposed heuristic algorithm, which is denoted as Alg_HA, is outlined as follows.

Algorithm Alg_HA

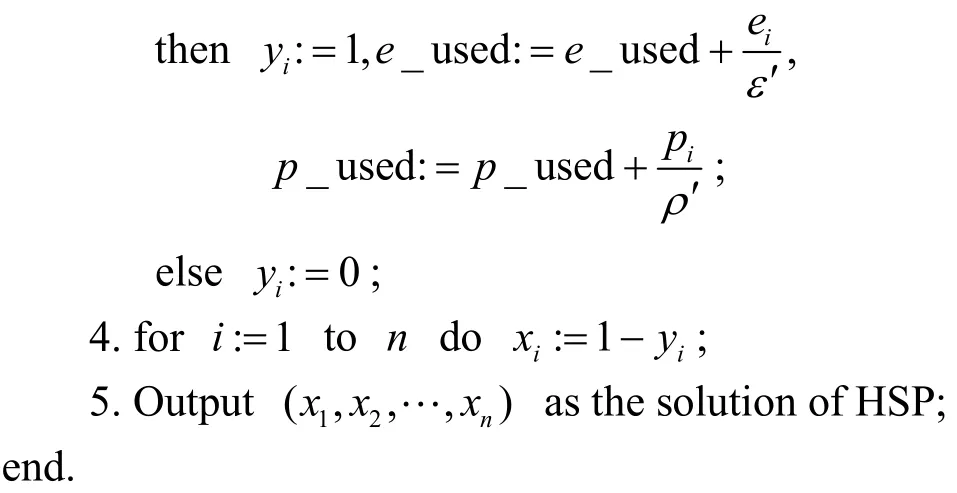
The time complexity of the proposed heuristic algorithm is dominated by the sorting process for the data set of n elements, and thus bounded by O(n log n)[22].The proposed heuristic algorithm Alg_HA is evaluated by an exact algorithm Alg_EA. Both Alg_HA and Alg_EA are simulated. The execution time and the power consumption in software and hardware are generated randomly in the simulation. The simulation results show that area penalties decrease for the problems with loose power constraints for a fixed time constraint, and the approximate solutions are nearly optimal.

With the development of profiling methodology,the hot path would be considered in the HW/SW partitioning model.

1.3 A New Model and Algorithm with Communications Penalty

The communications penalty is omitted in most algorithms which would be considered in a real embedded system. A new computational model is designed for the HW/SW partitioning problem in Ref. [23]. Based on the new model, a new dynamic programming algorithm is proposed which uses the source data to calculate the optimal solution directly.The new model proposed is based on the partitioning model employed in Ref. [12]. Figure 2 extends this model.

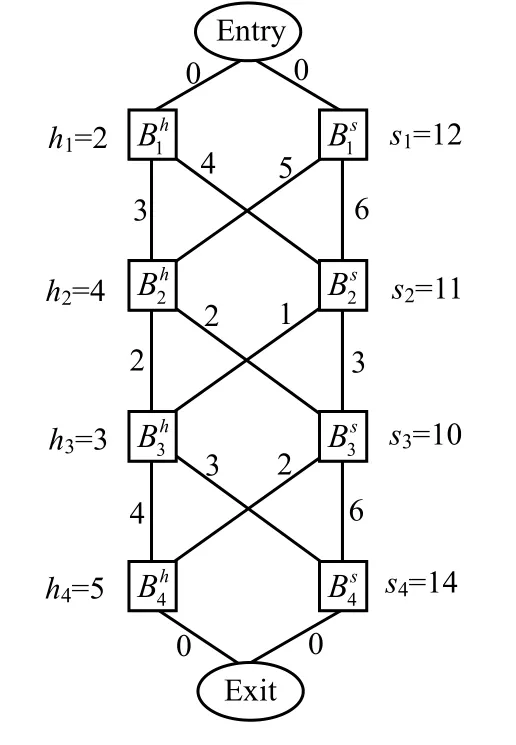
Fig.2 New model indicated by source execution time and all communication time

The application of the system corresponds to a sequence of n blocks, denoted as B1,B2,,Bn, that may be moved between hardware and software. The solution corresponding to the optimal path is subjected to the constraint of the available hardware area, and the length of the optimal path is as short as possible, in order to find the optimal path in a direct graph. In Fig.2,the communication penalty is considered in the new model.

The following notations are used in Fig. 2.communications derived from all possible HW/SW assignments of the neighboring blocks, utilizing the source data, rather than the extra speedup as mode of measurement.

Given available hardware areaA, the partitioning problem can be modeled as the following problem:

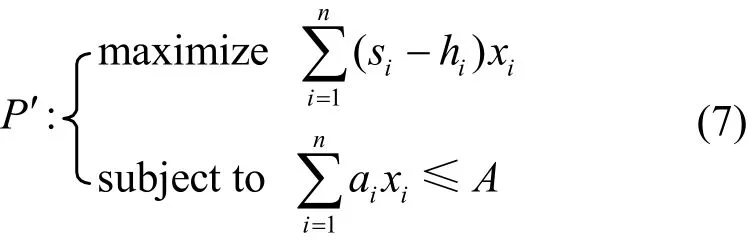
It is clear that P’ is the standard 0-1 knapsack problem of NP-complete[24].

The new algorithm for partitioning, called Alg_NAP, assigns one block at a time but is based on the new computational model as shown in Fig. 2. The Alg_NAP can be formalized to the following formula (8):

For formal description, see Ref.[23]. Simulation results show that the execution time of both algorithms increases with the number of the blocks in linear for a given hardware area A, and increases with the hardware area also in linear for a given number of the blocks. The execution time of the two algorithms also matches their time complexity O(n A) . Because Alg_NAP takes into account all types of the communications, Alg_NAP is able to solve the HW/SW partitioning problems more realistically than SPACE.

1.4 Power-efficient algorithm

Although there are several HW/SW partitioning techniques proposed over the last decade in which minimizing the execution time of the system is mainly considered, power efficiency is ignored or appears as one of the constraints which is one of the major considerations in the current HW/SW co-designs. A new model with objective of minimizing power consumption under the constraints of hardware area and execution time is proposed in Ref. [25]. An efficient heuristic algorithm with the execution time O(n logn) is proposed for the quality approximate solutions of the problems with n code fragments.

The efficient heuristic algorithm proposed is based on the partitioning model employed[26]. Fig. 3 shows the corresponding computational model for HW/SW partitioning with four blocks.

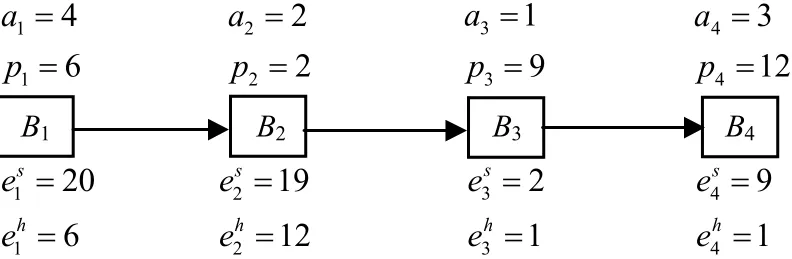
Fig.3 An example of the system model with four blocks

The given application of the system corresponds to a sequence of nblocks, denoted as B1,B2,,Bn,which may be moved between hardware and software.The blocks may be functions or procedures, in which the communication between the blocks can be omitted.

The following notations are used in Fig. 3.

The model discussed above focuses on yielding the minimal power consumption while having a total area penalty less than or equal to the available hardware controller area A and having an execution time less than or equal to the given constraint . Let X = [x1,x2,,xn], where xi∈ {0,1}, be a feasible solution of the partitioning problem which indicates the part Biis implemented in software or hardware.

The model proposed can be formulated as the following maximization problem for the givenAand :

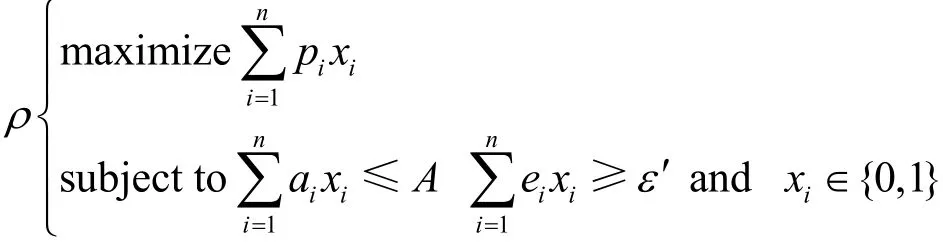
The larger the hardware area is, the shorter the execution time is, while the higher the power becomes generally. Usually the given constraints are loose enough to provide large space of the feasible solutions.So the program is reduced to the 0-1 knapsack problem as follows:

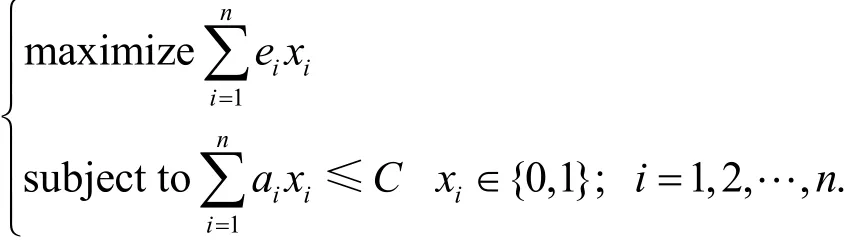
The heuristic algorithm, denoted as Alg_HEU and based on the model proposed, is outlined as follows.

Algorithm Alg_HEU

The time complexity of the proposed heuristic algorithm is dominated by the sorting process for the data set of n elements, and thus bounded by O(n log n)[24].

The proposed heuristic algorithm Alg_HEU is evaluated by an exact algorithm Alg_DPP. Both Alg_HEU and Alg_DPP are simulated. The simulation results show that the power saving becomes higher and higher for both Alg_DPP and Alg_HEU under the same time constraint with the increase of the available hardware area. The proposed heuristic algorithm Alg_HEU, running in O(n log n), is faster than the proposed exact algorithm Alg_DPP running in O(n Aε) for n code fragments under the hardware area constraint Aand the time constraint . Moreover, the algorithm Alg_HEU is able to get nearly optimal solution for small-sized problems, and thus it is reasonable to believe that the Alg_HEU is applicable to the large problem sizes in the HW/SW partitioning.

1.5 Functional Partitioning and Scheduling Algorithms

HW/SW partitioning decides which blocks of the given system could be implemented in hardware and which ones could be realized as software. HW/SW scheduling is the ordering of partitioned tasks in each processing element in such a way that a good processor utilization is achieved, and communication time between both internal tasks and inter-processor tasks is optimized[27-29]. It is well-known that partitioning and scheduling are the crucial steps during HW/SW co-design. The efficient heuristic algorithms for HW/SW partitioning and scheduling based on the architecture and constraints described[30]are proposed[31]. The proposed algorithms for partitioning and scheduling are combined. The proposed partitioning algorithm is based on a task graph[30]by iteratively moving the task with highest benefit-to-area ratio in higher priority. The proposed scheduling algorithm carries out the task based on hardware-only critical path in higher priority in task graph.

The proposed algorithms in Ref. [31] are based on task graphs described in Ref. [30]. A task graph is a directed acyclic graph (DAG)G =(T,E), where Tis the set of the tasks {t0,t1,,tn}, and E is the set of directed edges. In the task graph, each task node defines a functional unit of the program, which contains information about the computation the task needs to perform. A directed edge (ti,tj)inEdefines an immediate precedence constraint between task tiand task tj, in which (ti,tj) indicates that task tjcannot start until task tiis finished. Here, tiis called a predecessor of tj, and tjis called a successor of ti[30].

The following notations are used in the model and algorithms.

Given available hardware areaA, the partitioning problem proposed can be formularized as the following minimization problem:

The proposed partitioning algorithm deals with the communication penalty, which is an important factor for HW/SW partitioning, among tasks by merging it into the processing time of the tasks.Software tasks can communicate with others sequentially, and hardware tasks do concurrently in the DAG. The sv′ and hv′ are formularized as follows:

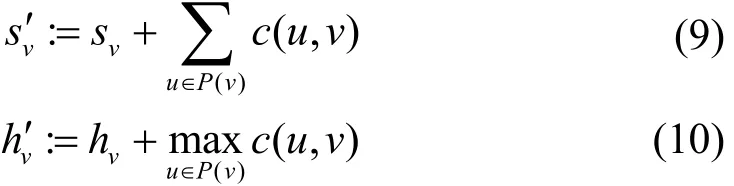
The task graph G is reduced to G′ by utilizing formula (9) and (10).

The benefit of moving the task v to hardware is denoted as bv, and the set of software tasks (including v) lying in the same precedence level of the software task v is denoted as Tv. bvis defined as follows:

The proposed heuristic algorithm, denoted as Alg_HA, is outlined as follows.

Algorithm Alg_HA

The communication penalty and the parallelizability between hardware tasks are taken into consideration in the scheduling algorithms proposed.The task scheduling is according to the task's priority.The algorithm calculates priorities for each task based on dynamic programming. In order to enhance the parallelism of the hardware tasks, the software task with highest priority, especially lying in the hardware-only critical path, is generally taken into the first consideration[31].

Let the taskudenote a predecessor of the v, then the communication factor of v corresponding to u,denoted as cof(u,v), is defined as follows:

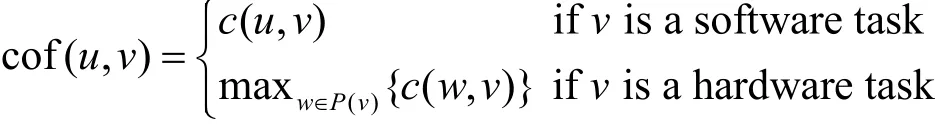
The software tasks are scheduled according to the priorities. The priority of u, denoted as pri(u), is formularized as follows:

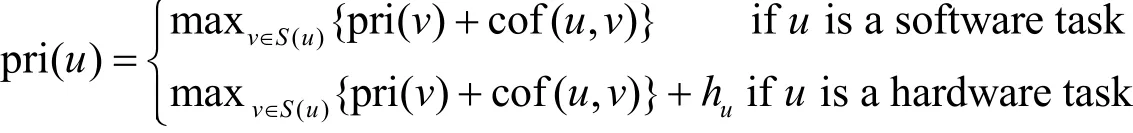
The following notations are defined in the scheduling algorithms.

The proposed scheduling algorithm which is

denoted as Alg_CPCS(G) is outlined as follows:

Input: task graph G;

Output: complete_time, the complete time of G;

Algorithm Alg_CPCS(G);

/*Critical-Path and Communication Combined Scheduler*/

/* All communication times related to t0are set to 0. */

/* The initial values of ready_time(ti), start_time(ti)and end_time(ti) are set to 0 for all i≤n.*/

For more details on algorithm Alg_CPCS(G), see Ref. [31].

Both Alg_HA and Alg_CPCS are simulated and compared with the previous algorithms as shown in Ref. [30]. The simulation results show that the proposed partitioning algorithm is comparable with the best combinatorial algorithm, and the proposed scheduling algorithm obtains the improvements over the traditional approaches by up to 10% without large increase in running time.

1.6 Algorithms for Path-based Hardware/Software Partitioning

With the development of profiling methodology,many powerful path profiling techniques have been reported in Refs. [32-34]. One path of higher execution frequency, called hot path which consists of the executed components with high frequency, dominates the whole execution time of the given application. The HW/SW partitioning for the given application can be approximately solved by efficiently partitioning the selected hot path. A path-based HW/SW portioning algorithm is proposed in Ref. [35], which is based on an extended computing model in which communication penalties between neighboring components are considered. In addition, an efficient tabu search algorithm is also implemented to refine the approximate solutions produced by the heuristic algorithm.

The model, as shown in Fig.2, takes all kinds of the communication time into account, no matter how the blocks implement.

The execution time can be formularized as:

The heuristic algorithm, denoted as Alg_HEA, is outlined below.

Algorithm Alg_HEA

/* A heuristic algorithm for HW/SWpartitioning, for the given n blocks and the available hardware area A. */begin

The time complexity of the algorithm Alg_HEA is bounded by O(n +k logn).

Tabu Search(TS) is one of the traditional heuristic-based algorithms to search for the global optimal solution for NP-hard problems[34-35]. A TS algorithm, denoted as Alg_TSA, is implemented to refine the heuristic solution generated by Alg_HEA.For more details on Alg_TSA, see Ref. [35].

A dynamic programming algorithm, denoted as Alg_DPA, is proposed to calculate the optimal solution of the problem P, in order to evaluate the performance of the algorithms Alg_HEA and Alg_TSA. The algorithms Alg_HEA, Alg_TSA and Alg_DPA are simulated.

The simulation results show that the heuristic algorithm Alg_HEA can be refined by Alg_TSA (heur)to a nearly optimal one, both for the computation-intensive case and for the communication-intensive case. The Alg_HEA is a fast algorithm to approximately solve the problem P, while the tabu search algorithm Alg_TSA can refine the approximate solution to a nearly optimal one within an acceptable runtime. The difference between the approximate solutions and the optimal ones is bounded by 0.5%, and it hardly increases with the increase of the problem size.

1.7 One Dimensional (1D) Search Algorithm

A model which was designed as an undirected communication graph for the embedded system to partitioned was proposed in Ref. [39]. Based on the model, a heuristic algorithm was proposed for the NP-hard version by searching a 2D solution space to obtain high quality candidate partitions. A type of hardware/software partitioning problems have been transformed into a 1D search problem in Ref [40],instead of a 2D search problem as described in Ref.[39]. Three low-complex algorithms are proposed with the lower bound of the solution quality for the hardware/software partitioning problem based on the new computing model.

The model proposed in Ref. [39] is based on the following notations.

Two versions of the partitioning problem were modeled in Ref. [39, 41].

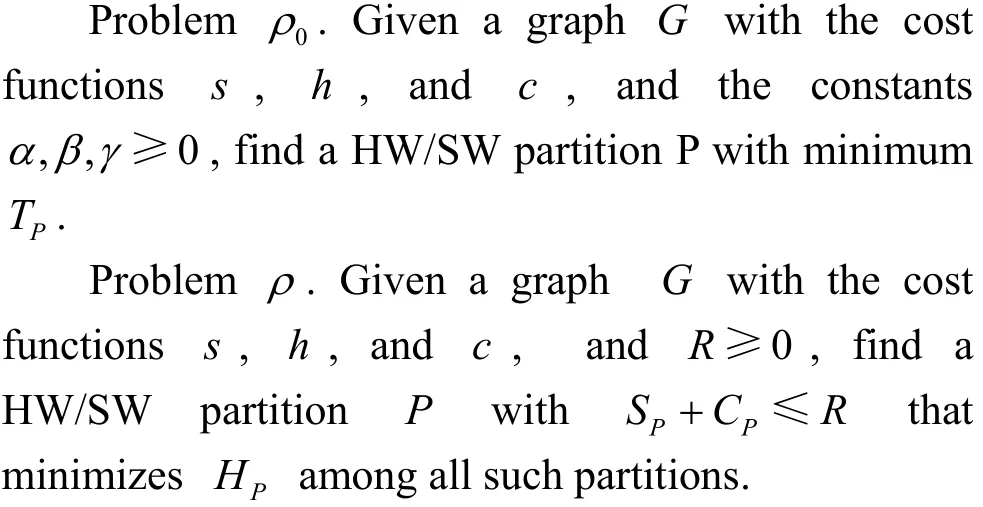
Thus, the HW/SW partitioning problem is approximately solved by searching 1D solution space.

Three algorithms, including Alg-new1, Alg-new2 and Alg-new3, for the problem are proposed based on 1D search problem for the problem . Alg-new1 only collects the feasible solutions of the problem Q for the final approximate optimal solution. Alg-new2,as an improved version for Alg-new1, is proposed in order to further promote the solution quality. The third algorithm, denoted as Alg-new3, is proposed to accelerate Alg-new2 while keeping the solution with higher quality. The following pseudocode shows the formal description of the Alg-new3.

Algorithm. Alg-new3

/*Searching 1D solution space (0, 1), from 1 to 0 with decrement ∆ , to find an approximate optimal solution of the problem Q.*/

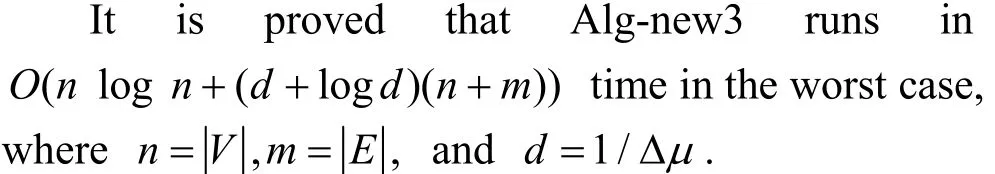
The algorithm Alg-new1, Alg-new2, Alg-new3,and the algorithm proposed in Ref. [39] have been implemented in C++. The empirical results show that the proposed three algorithms provide significant speedup in searching for approximate optimal solutions. These algorithms can produce better solutions with improvement of 14 percent on average and up to 50 percent for best cases. Moreover, the time complexity for partitioning a graph with n nodes and medges is significantly reduced from O(dxdyn3) to O(n log n + d(n + m)), where d and dx⋅dyare the number of the fragments of the searched 1D solution spaces. Also, the proposed lower bound is comparable to the old one proposed in Ref. [39].

2 Conclusion

We have provided a general view for HW/SW partitioning problem on different computing models.Different computing models and the corresponding algorithms are introduced for the HW/SW partitioning with different constraints. In addition, some potential problems on the complex system design have been proposed in this paper for future work.

[1] GUPTA R K, COELHO C N, DE MICHELI G. Synthesis and simulation of digital systems containing interacting hardware and software components[C]//Proc the 29th ACM/IEEE Design Automation Conference. Los Alamitos,CA, USA: ACM Press, 1992: 225-230.

[2] GUPTA R K, DE MICHELI G. Hardware-software cosynthesis for digital systems[J]. IEEE Design and Test of Computers, 1993, 10 (3) : 29-41.

[3] NIEMANN R, MARWEDEL P. Hardware/software partitioning using integer programming[C]//Proc the IEEE/ACM European Design Automation Conference(EDAC). Paris, France: IEEE Computer Society Press, 1996:473-479.

[4] ERNST R, HENKEL J, BENNER T. Hardware-software co-synthesis for micro-controllers[J]. IEEE Design and Test of Computers, 1993, 10 (4): 64-75.

[5] VAHID F, GAJSKI D D, GONG J. A binary-constraint search algorithm for minimizing hardware during hardware/software partitioning[C]//Proc IEEE/ACM European Design Automation Conference (EDAC). Paris,France: IEEE Computer Society Press, 1994: 214-219.

[6] VAHID F, GAJSKI D D. Clustering for improved system-level functional partitioning[C]//Proc the 8th International Symposium on System Synthesis. Cannes,France: ACM Press,1995: 28-33.

[7] PENG Z, KUCHCINSKI K. An algorithm for partitioning of application specific system[C]//Proc of IEEE/ACM European Design Automation Conference (EDAC). Paris,France: IEEE Computer Society Press, 1993: 316-321.

[8] HENKEL J, ERNST R. An approach to automated hardware/software partitioning using a flexible granularity that is driven by high-level estimation techniques[J]. IEEE Transactions on Very Large Scale Integration (VLSI)Systems, 2001, 9(2): 273-289.

[9] NIEMANN R, MARWEDEL P. An algorithm for hardware/software partitioning using mixed integer linear programming[J]. Design Automation for Embedded Systems,1997, 2 (2): 165-193.

[10] WEINHARDT M. Integer programming for partitioning in software oriented codesign[C]//Proceedings of the 5th International Workshop on Field-Programmable Logic and Applications. London: Springer-Verlag,1995: 227-234.

[11] MADSEN J, GRODE J, KNUDSEN P V, et al. LYCOS:the lyngby co-synthesis system[J]. Design Automation for Embedded Systems, 1997, 2(2): 195-235.

[12] WU Ji-gang, SRIKANTHAN T. Low-complex dynamic programming algorithm for hardware/software partitioning[J]. Information Processing Letters, 2006, 98(2):41-46.

[13] EDWARDS S, LAVAGNO L, LEE E A, et al. Design of embedded systems: formal models validation, and synthesis[J]. Proceedings of the IEEE, 1997, 85 (3):366-390.

[14] O’NILS M, JANTSCH A, HEMANI A, et al. Interactive hardware-software partitioning and memory allocation based on data transfer profiling[C]//Proc Int’l Conf Recent Advances in Mechatronics. Turkey: Bogazici University Publication, 1995: 447-452.

[15] SRINIVASAN V, RADHAKRISHNAN S, VEMURI R.Hardware/software partitioning with integrated hardware design space exploration[C]//Proc Conf Design,Automation and Test in Europe. Paris, France: IEEE Computer Society Press, 1998: 28-35.

[16] DICK R P, JHA N K. MOGAC: a multiobjective genetic algorithm for hardware-software cosynthesis of distributed embedded systems[J]. IEEE Trans.Computer-Aided Design of Integrated Circuits and Systems, 1998, 17(10): 920-935.

[17] HENKEL J, ERNST R. An approach to automated hardware/software partitioning using a flexible granularity that is driven by high-level estimation techniques[J]. IEEE Trans. Very Large Scale Integration Systems, 2001, 9(2):273-290.

[18] GRODE J, KNUDSEN P V, MADSEN J. Hardware resource allocation for hardware/software partitioning in the LYCOS system[C]//Proc Conf Design, Automation and Test in Europe. Paris, France: IEEE Computer Society Press, 1998: 22-27 .

[19] LOPEZ-VALLEJO M, LOPEZ J C. On the hardware-software partitioning problem: system modeling and partitioning techniques[J]. ACM Transactions on Design Automation of Electronic Systems, 2003, 8(3):269-297.

[20] RAY A, WU Ji-gang, SRIKANTHAN T. Knapsack model and algorithm for hardware/software partitioning problems[J]. Computing and Informatics, 2004, 23(5):1001-1013.

[21] WU Ji-gang, SRIKANTHAN T. Algorithmic aspects of area-efficient hardware/software partitioning[J]. The Journal of Supercomputing, 2006, 38(3):223-235.

[22] KNUTH DE. The art of computer programming (Volume 3), Sorting and Searching[M]. 2nd ed. USA:Addison-Wesley Professional, 1998: 74-81.

[23] WU Ji-gang, SRIKANTHAN T, ZOU G W. New model and algorithm for hardware/software partitioning[J].Journal of Computer Science and Technology, 2008, 23(4):644-651 .

[24] PISINGER D. Algorithms for knapsack problems[D].Copenhagen: University of Copenhagen, 1995.

[25] WU Ji-gang, SRIKANTHAN T, YAN Cheng-bin.Algorithmic aspects for power-efficient hardware/software partitioning[J]. Mathematics and Computers in Simulation,2008, 79(4): 1204-1215.

[26] MARTELLO S, TOTH P. Knapsack problems: algorithms and computer implementations[M]. New York: John Wiley& Sons Inc, 1990: 197-210.

[27] TAHAEE S-A, JAHANGIR A H. A polynomial algorithm for partitioning problems[J]. ACM Transactions on Embedded Computing Systems, 2010, 9(4):1-38.

[28] YUAN Ming-xuan, GU Zong-hua, HE Xiu-qiang, et al.Hardware/software partitioning and pipelined scheduling on runtime reconfigurable FPGAs[J]. ACM Transactions on Design Automation of Electronic Systems, 2010, 15(2):1-41.

[29] ALI U, MALIK M B. Hardware/software co-design of a real-time kernel based tracking system[J]. Journal of Systems Architecture, 2010, 56(8): 317-326.

[30] WIANGTONG T, CHEUNG P Y K, LUK W. Comparing three heuristic search methods for functional partitioning in hardware-software codesign[J]. Design Automation for Embedded Systems, 2002, 6(4):425-449.

[31] WU Ji-gang, SRIKANTHAN T, JIAO Tao. Algorithmic aspects for functional partitioning and scheduling in hardware/software co-design[J]. Design Automation on Embedded Systems, 2008, 12(4): 345-375.

[32] BALL T, LARUS J R. Efficient path profiling[C]//Proc of the 29th Annual ACM/IEEE International Symposium on Microarchitecture. Washington: IEEE Computer Society,1996: 46-57 .

[33] DUESTERWALD E, BALA V. Software profiling for hot path prediction: Less is more[C]//Proc 9th Int conf Architectural Support for Programming Languages and Operating Systems. Cambridge: IEEE Computer Society,2000: 202-211.

[34] MELSKI D, Interprocedural path profiling and the interprocedural express-lane transformation[D]. Wisconsin:University of Wisconsin, 2002.

[35] APIWATTAN APONG T, HARROLD M J. Selective path profiling[C]// Proc ACM SIGPLAN-SIGSOFT Workshop on Program Analysis for Software Tools and Engineering.New York: ACM Press, 2002, 28(1): 35-42.

[36] BALAS E, ZEMEL E. An algorithm for large zero-one Knapsack problems[J]. Operations Research, 1980, 28(5):1130-1154.

[37] GLOVER F. Future paths for integer programming and links to artificial intelligence[J]. Computers and Operations Research, 1986, 13(5): 533-549.

[38] GLOVER F, LAGUNA M. Tabu Search[M]. MA, USA:Kluwer Academic Publishers, 1997:134-142.

[39] ARATO P, MANN Z A, ORBAN A. Algorithmic aspects of hardware/software partitioning[J]. ACM Transactions on Design Automation of Electronic Systems, 2005, 10(1):136-156.

[40] WU Ji-gang, SRIKANTHAN T, CHEN Guang.Algorithmic aspects of hardware/software partitioning: 1D Search Algorithms[J]. IEEE Transactions on Computers,2010, 59(4): 532-544.

[41] ARATO P, JUHASZ S, MANN Z A, et al.Hardware-software partitioning in embedded system design[C]//IEEE International Symposium on Intelligent Signal Processing. USA: IEEE Standards, 2003: 197-202.

软硬件协同设计复杂问题的计算模型和算法

叶 华，武继刚

(天津工业大学计算机科学与软件学院 天津 西青区 300387)

软硬件划分是设计复杂嵌入式系统的关键环节。论文综述了近年来提出的解决软硬件划分问题的计算模型和相应算法。软硬件划分问题可以建模成各种限定不同约束条件的背包问题模型，同时需要考虑任务块间的通信消耗。背包问题中的子项相当于软硬件划分问题中的任务块。论文针对不同的计算模型，介绍了相应的精确算法和启发式算法。论文最后探讨了若干待研究的潜在问题。

算法; 复杂系统; 计算模型; 软硬件划分

TP301.6

A

10.3969/j.issn.1001-0548.2011.03.002

2011 − 04 − 10

国家自然科学基金(60970016)

叶 华(1976 − )，女，讲师，主要从事嵌入式系统软硬件协同设计方面的研究.

date： 2011 − 04 − 10

Supported by the National Natural Science Foundation of China under Grant(60970016)

Biography：YE Hua was born in 1976, and her research interests include hardware/software co-design in embedded systems.

编 辑 蒋 晓