总装材料对氦气吸附性能的试验研究

薛长利，刘伟强

（1.国防科技大学 航天与材料工程学院，长沙 410073；2.航天东方红卫星有限公司，北京 100094）

0 引言

航天器的密封性能关系着航天器飞行的寿命及可靠性[1-2]，需要通过检漏等无损检测手段来保证航天器推进系统的装配质量。在航天器推进系统密封性的检测及试验研究中，氦质谱检漏经常作为重要的方法和手段[3]。在卫星研制过程中所采用的检漏方法主要有氦质谱正压单点检漏法、氦质谱正压积累检漏法和氦质谱正压真空检漏法。目前，我国卫星出厂前整星检漏和发射场整星检漏均采用氦质谱正压积累检漏法[4]。

在采用正压积累法进行检漏，普遍认为：在试验的过程中，由于卫星总装材料、积累容器材料等对氦气有吸附作用，会对卫星的检漏试验数据造成影响[5]。鉴于没有相关研究以及数据，我们对卫星总装过程中所使用的部分材料的吸附性进行了宏观的研究，探讨总装材料对检漏结果的影响。分子间的相互作用。它们之间的相互作用力有范德瓦尔斯力和化学键力两种形式，分别对应于物理吸附和化学吸附的宏观现象。物理吸附的特点是吸附比较弱，对吸附质一般无选择性，温度越低吸附量越大，且可以形成多层吸附。而化学吸附的特点是吸附比较强，对吸附质有选择性，只能形成单层吸附[6]。

氦气与纱布等总装材料的吸附为物理吸附，适用BET吸附等温线，即在相同的温度条件下，氦气与总装材料的吸附是多分子层吸附。按照气体吸附理论，第一层氦气分子在总装材料表面吸附后尚能提供足够强的吸引力产生第二层甚至更多层，尤其在低温下的物理吸附可形成多层分子吸附。BET吸附等温线的方程表达式[6]为

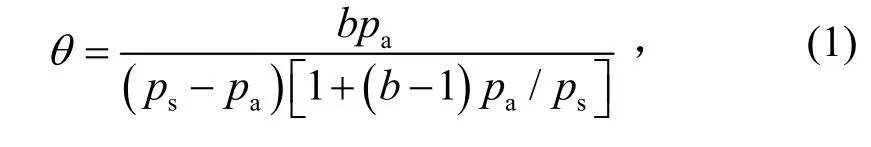
1 试验原理

1.1 吸附机理

当气体和固体表面处于平衡态时，靠近固体表面的气体密度总是大于远离表面的密度，这说明固体表面有俘获气体分子并使其滞留于表面附近的能力。这种气体被固体表面俘获而附着于表面上的现象称为吸附现象。承担吸附作用的物质称为吸附剂，被吸附的物质称为吸附质。

吸附现象的本质是固体表面分子与气体表面

式中： pa为吸附分子的平衡气体压强；ps为同一温度时气体的饱和蒸气压；b为常数，与吸附热及汽化热有关；θ为覆盖度，表示被气体占据的吸附中心数与总吸附中心数之比。

对覆盖度为θ的吸附表面，其吸附的气体摩尔数[6]为

式中：σ为实际吸附分子的量；N0为吸附中心数，根据研究，布满1 cm2表面的单分子层分子数约为

1015个；NA为阿伏加德罗常数，NA=6.02×1023mol-1。氦气在常温常压下理想气体状态方程[6]

式中：p为气体压力；V为气体体积；n为气体的摩尔数；R为普适气体常量；T为气体的绝对温度。

1.2 检漏试验吸附模型

正压积累检漏试验中的吸附材料长期处于大气环境中，材料的吸附中心已经吸附了氮气、氧气、水蒸气等大气中的气体分子，并处于动平衡状态。在试验过程中，氦气体积分数缓慢增加，部分氦气随之吸附到吸附材料表面，并达到新的动态平衡。

正压积累检漏试验中的氦气分配如图1所示。卫星推进系统内的氦气向积累容器泄漏，其中一部分使得积累容器中的氦气体积分数增加，另一部分被吸附材料表面捕获并吸附。在积累一段时间后，积累容器内氦气的体积分数变化为

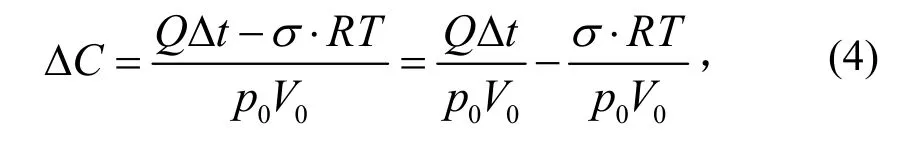
式中：∆C为氦气在积累容器中的体积分数变化；Q为卫星或者标准漏孔的漏率；∆t为积累有效时间；p0为积累容器内气体总压力；V0为积累容器内气体总体积。

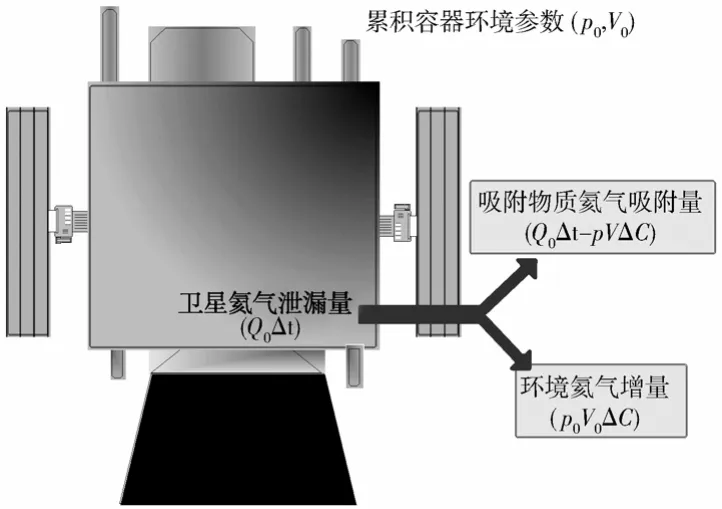
图1 检漏试验氦气分配示意图Fig.1 Schematic diagram of helium distribution in leakage test

根据体积分数定义，氦气的体积分数为由式(1)～式(5)，并令A=N0RT/NA，由于正压积累检漏中pa＜＜ps，用ps代替ps-pa后得

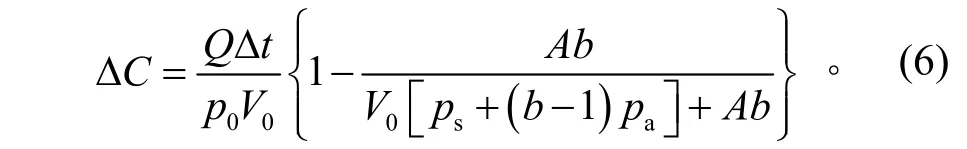
由于氦质谱仪显示值与实际体积分数成线性关系，通过氦质谱仪对氦气体积分数进行测量，氦质谱仪的测量值与氦气体积分数的转换关系可以表示为

式中：∆I为氦质谱仪对应积累容器中的体积分数的增加值；k为转换系数，通过对氦质谱仪标定获得。

2 试验设计

2.1 试验目的

在正压积累检漏试验过程中，卫星周围的环境为大气环境，氦气的体积分数一般在5×10-6～7×10-6之间，卫星的实际漏率在10-6Pa·m3·s-1量级。此试验研究的目的是总装材料吸附性对卫星整星检漏结果的影响。

2.2 试验装置

试验装置如图2所示。

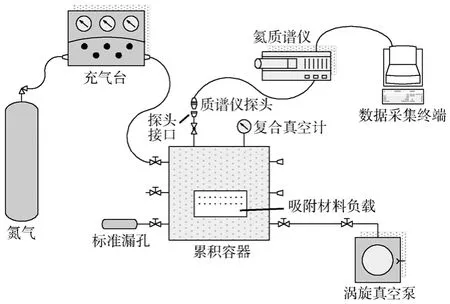
图2 总装材料吸附性试验装置Fig.2 Schematic diagram of test equipment for adsorption capability test of assembly materials

试验装置主要设备有：

1）积累容器。为φ400 mm×400 mm圆柱体内腔，具有KF25法兰接口以及专用探头接口。采用不锈钢材料，内部表面抛光处理。

2）氦质谱仪。Inficon UL1000型氦质谱仪在吸检模式下最小可检漏率为1×10-9Pa·m3·s-1。

3）充气台。用于向积累容器充入规定压力的高纯气体，出口压力范围0～2.5MPa。

4）标准漏孔。用于提供固定氦气流量，标称漏率1.9×10-6Pa·m3·s-1。

5）涡旋真空泵。用于对积累容器的抽真空，容器极限真空度10-2Pa。

6）其他试验用品还包括高纯氮气、管路及阀门组件、计时器等。

氦质谱仪通过数据线与计算机串行接口相连，试验过程数据通过软件自动采集和记录。

2.3 试验方法

在进行负载试验前，为了取得在没有任何吸附材料而仅有积累容器本身内壁吸附时的本底数据，需要进行空载测试，方法如下：

1）将没有试验负载的积累容器真空度抽至优于0.1 Pa，并在该真空度下保持15min；

2）用充气台向积累容器充入高纯氮气，充气压力至1～1.1 atm，然后关闭充气阀门；

3）以较小开度打开积累容器放气阀门，将积累容器放气至与外界压力相同，然后关闭阀门；

4）打开标准漏孔阀门，并开始计时，经过一定时间后关闭漏孔阀门；

5）等待积累容器内氦气稳定一定时间后，用氦质谱仪通过测量口测试容器内氦气体积分数；

6）重复步骤4）～5），测试不同积累时间后容器内的氦气体积分数。

在完成空载试验后，将试验负载放入积累容器，按照与空载相同的方法进行试验。

3 试验实施及分析

3.1 反应时间测试

为了获得在施加氦气后积累容器中氦气扩散达到稳定状态所需要的时间，分别在空载、纱布负载2以及多层负载三种情况下进行了氦气扩散反应时间测试，测试结果见图3。

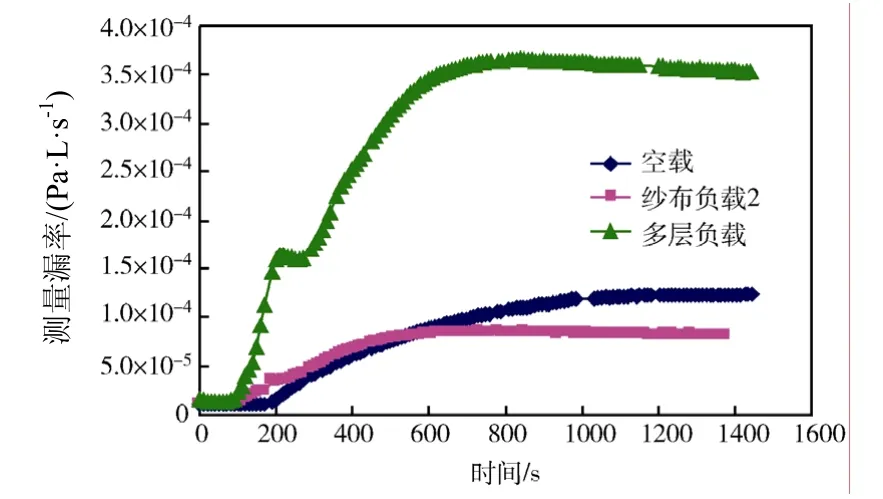
图3 氦气扩散时间曲线Fig.3 Balance time of helium diffusing in test chamber

从测试曲线可以看出：在不同负载的情况下，氦气在积累容器中达到均衡稳定的时间有较大差异，时差范围为10～25min。因此试验中各数据点的采集时间间隔应大于各自稳定时间。同时，由于测试中施加的氦气量不同，造成平衡后的氦气体积分数也存在差异。

3.2 试验内容

积累试验分别进行了空载、纱布负载1、纱布负载2、海绵负载以及多层负载五种情况的试验。4种负载材料性能参数见表1。

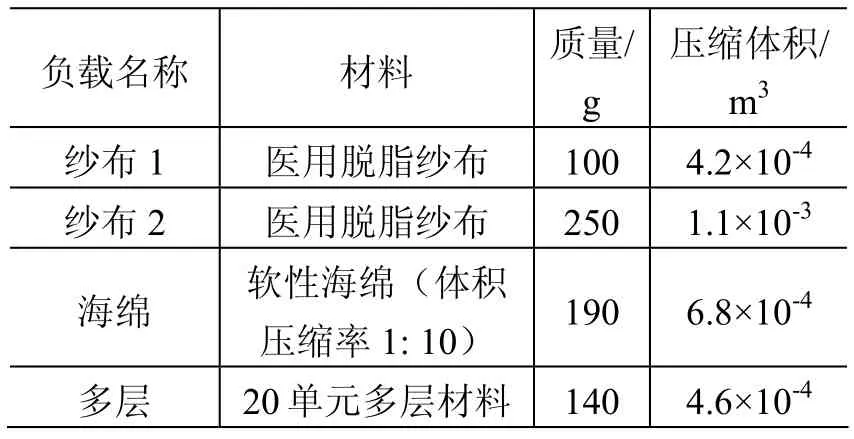
表1 试验用吸附性负载材料Table 1 Absorptive loads used in tests

根据对实测数据的理论分析，按照最小二乘法对数据进行线性回归处理，获得对应的回归曲线。为了验证试验的重复性，在相同情况下均进行了多次测试，在数据处理中，同一负载的试验顺序分别用T1、T2、T3表示。

3.3 试验结果及分析

3.3.1 积累容器空载试验分析

空载测量漏率-时间曲线如图4所示。

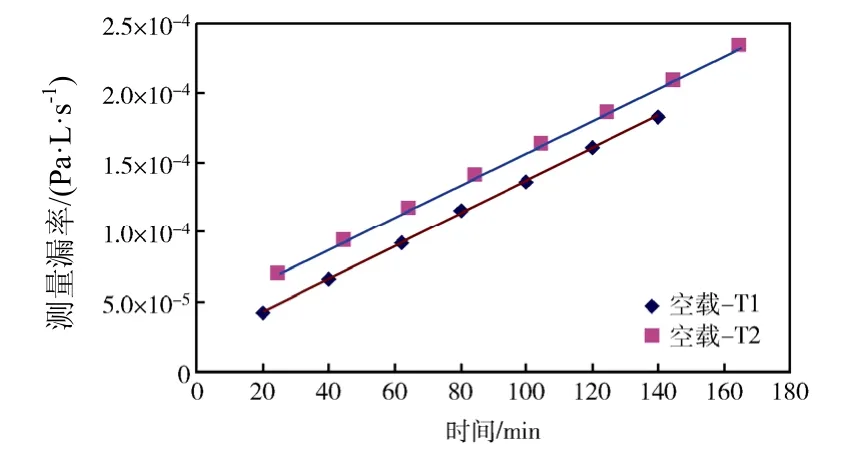
图4 空载测量漏率随时间增长的回归曲线Fig.4 Regression curves of helium concentration growth in tests without load

表2给出了空载数据回归曲线参数，可以看出，积累容器内的氦气体积分数与漏孔积累时间成线性关系。由式(4)可知，整个积累试验中影响氦气体积分数的主要因素有两部分：一部分是标准漏孔提供的恒定流量的氦气，使容器内的氦气体积分数随时间按线性比例增加；另一部分是由于容器内壁的吸附造成氦气体积分数的下降。由于容器内壁经过抛光处理，其物理表面积较小，可以判断容器内壁存在以下两种可能：

1）容器壁对氦气的吸附很小，对标准量级漏孔的积累没有影响；

2）容器壁对氦气的吸附较大，但其吸附规律符合线性关系。

对于以上两种情况，因为试验条件相同，故可以通过比较空载和负载情况下的测量漏率增长速度的差异来确定负载的吸附量。

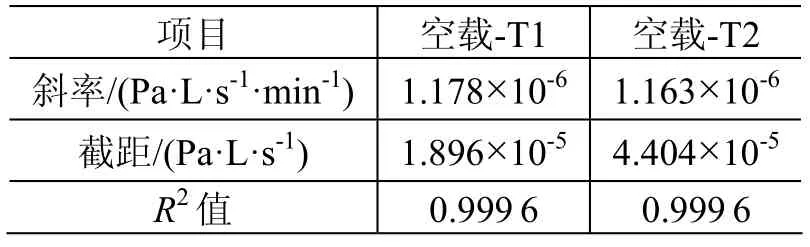
表2 空载数据回归曲线参数Table 2 Parameters of regression curves in tests without load

3.3.2 积累容器负载试验分析

各个负载试验的数据回归曲线及参数如图5～图8及表3～表6所示。

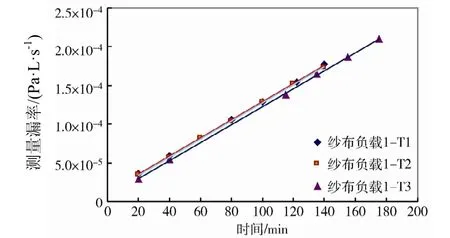
图5 纱布负载1下测量漏率增长的回归曲线Fig.5 Regression curves of helium concentration growth in tests with gauze pieces group No.1

表3 纱布负载1的数据回归曲线参数Table 3 Parameters of regression curves in tests with gauze pieces group No.1

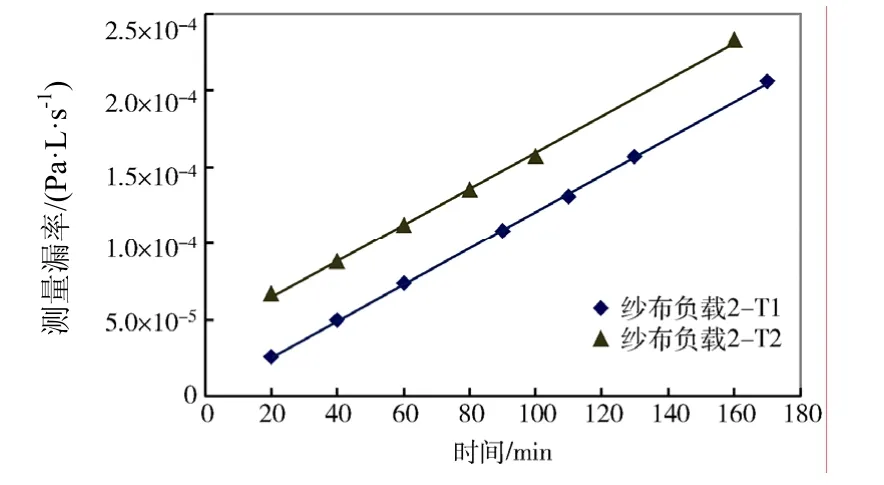
图6 纱布负载2下测量漏率增长的回归曲线Fig.6 Regression curves of helium concentration growth in tests with gauze pieces group No.2

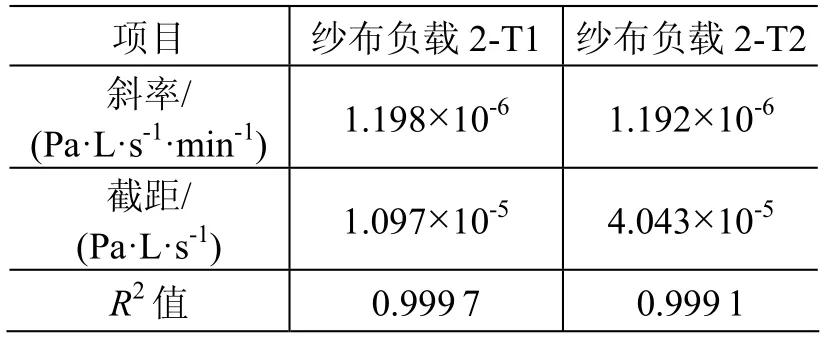
表4 纱布负载2的数据回归曲线参数Table 4 Parameters of the regression curve in tests with gauze pieces group No.2

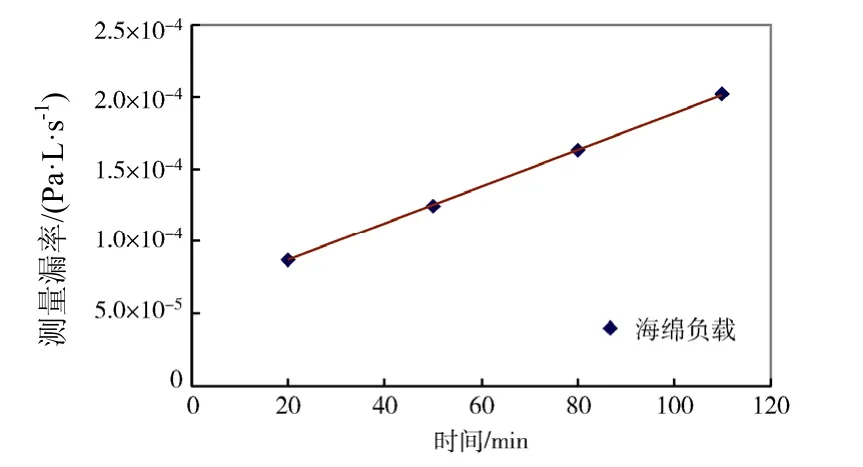
图7 海绵负载下测量漏率增长的回归曲线Fig.7 Regression curve of helium concentration growth in tests with sponge blocks

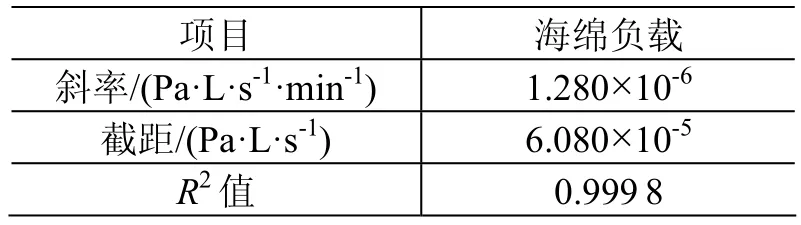
表5 海绵负载的数据回归曲线参数Table 5 Parameters of the regression curve in test with sponge blocks

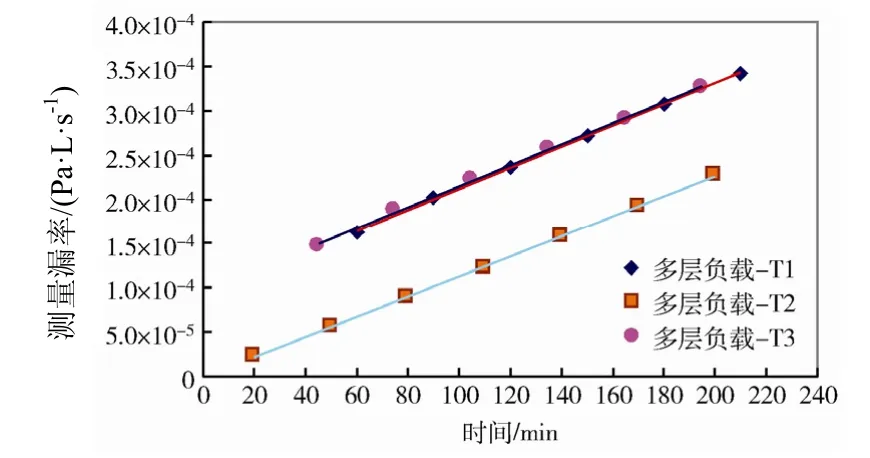
图8 多层负载下测量漏率增长的回归曲线Fig.8 Regression curves of helium concentration growth in tests with multilayer heat reflection components

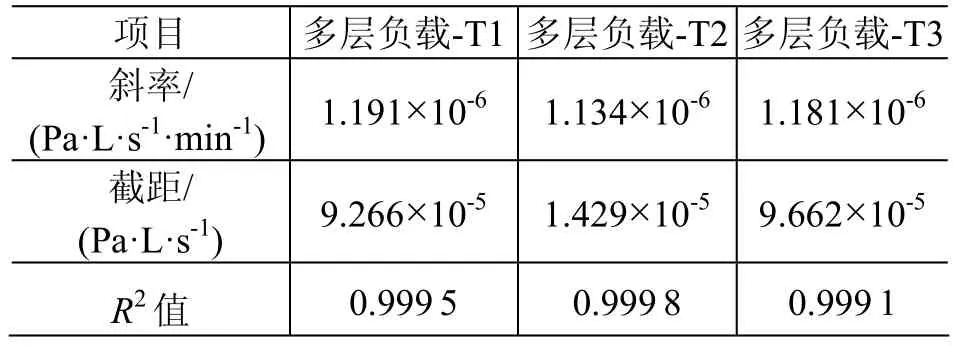
表6 多层负载的数据回归曲线参数Table 6 Parameters of regression curves in tests with multilayer heat reflection components

通过各组负载多次重复试验表明：试验装置的重复性较好，根据回归曲线的斜率进行统计分析，试验重复性误差均小于 5%，其中包括氦质谱仪稳定性、操作、计时、校准环境变化等环节引入的误差。

回归曲线的截距均存在差异，即每次试验的起始点均有所不同。经过对试验方法的分析，造成此差异的主要原因在于：在对容器抽真空后进行充气、复压、泄压的过程中，由于在大气环境下操作，使得部分空气进入容器后，造成了初始氦气体积分数的不同，影响了测量的初始值。

按照式(4)计算负载体积对积累容器有效容积的影响，结果如表7所示。其中V0表示积累容器容积，VL表示负载的压缩体积，(V0-VL)为加入负载材料后积累容器的有效容积。按照计算结果分析，试验用负载的体积对氦气体积分数的影响均为正值，表明有负载情况下测量漏率的增长速度大于空载情况下的增长速度。

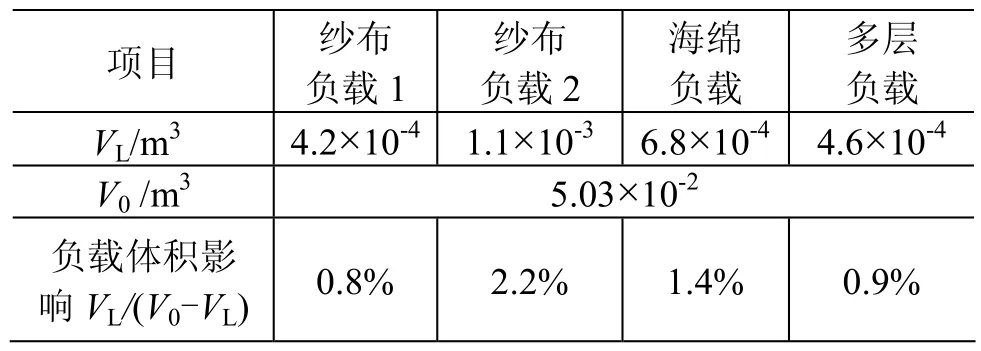
表7 负载体积对测试结果的影响Table 7 Effect of load volume on test results

表8统计列出了多次负载试验的分析结果，其中斜率均值为各组测试曲线的斜率平均值，增减幅为各组负载均值相对空载均值的增减幅度，吸附的影响量按照以上两项的差值。吸附的影响量中实际上包括了系统误差以及随机误差等不可直接测量项。吸附的影响在理论上应该为负值。

表8 负载试验测试结果分析Table 8 Analysis of test results with load

结合各曲线及其回归参数进行分析，在试验条件下，通过与空载下测量漏率积累数据曲线的斜率进行比较，纱布以及多层材料对测量漏率积累的影响较小，综合系统误差、重复性误差在内的情况下，其误差均不大于2%。而按照BET吸附方程及式(6)通过参考氦气吸附参数的测量值[6-7]，经过计算分析，式中的Ab/{V0[ps+(b-1)pa]+Ab}部分是个极小量，其数值远小于1，采用正压检漏时负载的吸附对检漏结果基本没有影响。

通过图6及表8所示的海绵负载的测量数据回归曲线发现，其斜率不但比空载没有减小，反而有所增大。原因分析如下：按照外形尺寸计算，海绵体积为6.8×10-3m3，而容器容积为5.03×10-2m3，减小为原来容积的0.865。用式(6)及式(7)进行分析，对应的斜率应比空载时增加15.6%；按照海绵压缩尺寸计算，由表7可知其对应的斜率应比空载时增加1.4%。但实际测试结果只比空载下增加了9%。这说明不能按海绵的外形尺寸或压缩尺寸计算负载体积，因为海绵为多孔结构，其体积对检漏结果的影响应该介于外形尺寸和压缩尺寸的影响之间。造成这一现象的原因是氦气向海绵中扩散的速度较慢，在试验的测试时间内，没有完全在海绵中扩散均匀。

综合了系统误差、随机误差在内的吸附影响量为正值，说明海绵负载材料体积影响超过了吸附的影响，需要对VL的取值进行修正，使其更接近实际情况。

实际上，正压检漏中的负载与积累容器的体积比要比试验中的情况小得多，使得VL/(V0-VL)的值小于0.1%。在这种情况下，以上所有的负载体积对检漏结果的影响都很小，可忽略不计。同时，吸附材料的吸附中心数与容器体积的比值也降低很多，材料吸附对检漏结果的影响则更小。由此看来，对检漏结果影响更大的主要是试验的系统误差和随机误差。

4 结束语

本文通过理论及试验分析表明，在卫星的正压检漏试验中，纱布、海绵、多层等材料的氦吸附作用对检漏试验的影响很小。在采用容积较大的积累容器时，更大的影响来源于系统误差和随机误差，例如积累容器有效容积的测量误差、氦质谱仪的长期稳定性等因素。所以在使用大容积积累容器检漏试验时，应该对系统的其他影响因素进行分析。

（References）

[1]Hammock W R, Cota P E, Rosenbaum B J, et al.Investigative techniques used to locate the liquid hydrogen leakage on the Space Shuttle Main Propulsion System, AIAA 91-1936[R], 1991

[2]肖祥正.质谱检漏技术在我国航天工业领域中的应用(一)[J].真空与低温, 2001, 7(4): 194-199 Xiao Xiangzheng.Application of mass spectrometer leak detecting technology in china Space industry[J].Vacuum and Cryogenics, 2001, 7(4): 194-199

[3]Tomohiro Yokozek, Takahira Aoki, Takashi Ishikawa.Experimental cryogenic gas leakage through damaged composite laminates for propellant tank application[J].Journal of Spacecraft and Rockets, 2005, 42(2): 363-366

[4]肖祥正.质谱检漏技术在我国航天工业领域中的应用(二)[J].真空与低温, 2002, 8(1): 8-11 Xiao Xiangzheng.Application of mass spectrometer leak detecting technology in china space industry[J].Vacuum and Cryogenics, 2002, 8(1): 8-11

[5]师立侠, 闫荣鑫.氦质谱大气累积检漏法误差分析[C]//第十四届全国质谱分析和检漏会议、第九届全国真空计量测试会论文汇编, 2007

[6]达道安.真空设计手册[M].3版.北京: 国防工业出版社, 2006

[7]王宝霞, 张世伟.真空工程理论基础[M].沈阳: 东北大学出版社, 1997