复杂二端网络电阻的求解方法研究

张洪宝

德州职业技术学院电子与新能源技术工程系 山东德州 253034

复杂二端网络电阻的求解方法研究

张洪宝

德州职业技术学院电子与新能源技术工程系 山东德州 253034

介绍特殊无源线性二端网络等效电阻的求解方法。一个正方体的每个棱都是一个电阻R，如何求出这个正方体的对角顶点间的电阻？这个问题用解决串并联的方法行不通。主要利用欧姆定律和电阻的星（Υ）—三角（△）变换等几种不同的方法解决这一问题，为电路的分析计算提供有效帮助。

二端网络；电阻；欧姆定律；Υ-△变换

1 前言

电路计算中，常常需要对二端网络电阻进行计算。对于一般的混联电路，可以用解决串并联的方法进行逐步化简，然后求出等效电阻。但是，对于既不是串联也不是并联的特殊电阻电路，求等效电阻就不是那么容易了。为此，笔者找出简单、方便的方法。

2 特殊二端网络电阻求解方法

如图1所示，正方体的每条棱都是一个电阻R，试问这个正方体的对角顶点A、c间的电阻是多少？这一问题如果用通常的求解电阻串并联的方法是无法解决的，必须寻找其他的方法。本文提出新的方法解决这一问题。

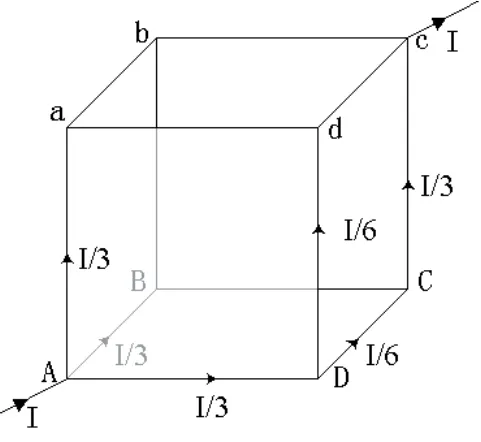
图1

2.1 利用欧姆定律求解

1）假设在顶点A输入电流I，在c端流出电流I。根据电路的对称性，在Aa、AB和AD三个棱上的电流将是I/3。同理，在DC和Dd两个棱上的电流将是I/6，而在Cc棱上的电流是I/3，由c端流出的电流仍将是I。

2）求出Ac两端的电压。根据电压的有关知识可知，Ac两端的电压等于AD、DC和Cc三棱上电压的和，即

2.2 利用电阻的Υ-△变换求解

将da、dc、dD和BA、Bb、BC进行Υ-△变换，得到图2。

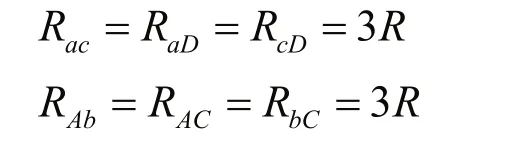
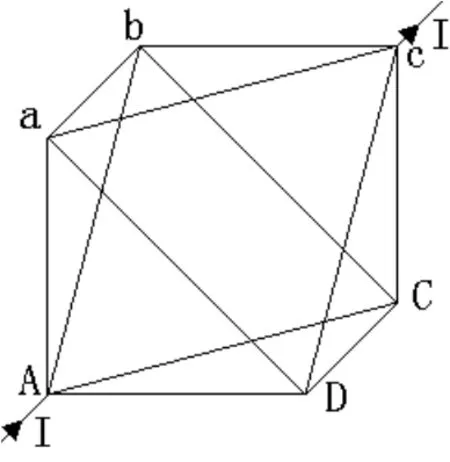
图2

在该图中，观察电路的结构会发现，电路的A、a、b、c侧和A、D、C、c侧是对称的，a点与D点对称，b点与C点对称。如果在A和c两端加上电压的话，那么，a点与D点、b点与C点是等电位点，在支路aD和bC中的电流将为零。因此，根据电路理论，可以将支路aD和bC去掉，将图2简化为图3。

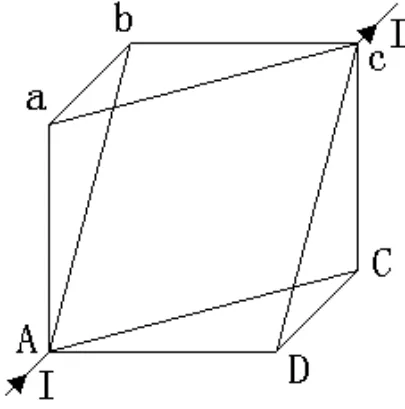
图3

将图3变形，即为图4。从图4可以看出，该电路是由对称的两部分电路并联而成。现在将bA、ba、bc和CA、Cc、CD分别进行△—Υ变换，便得到图5。

根据△-Υ变换公式，可以求出o1a、o1b和o1c的电阻。

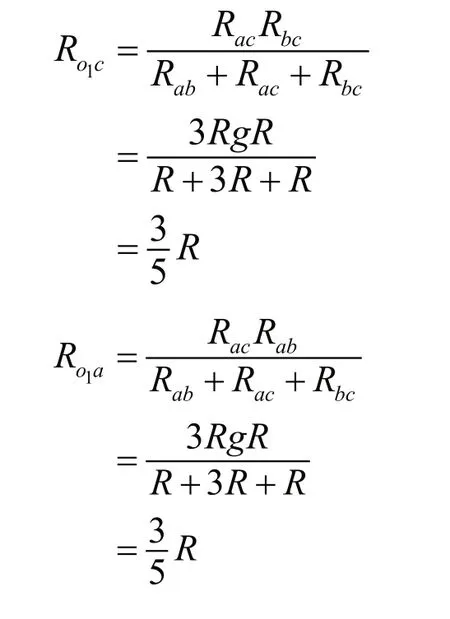
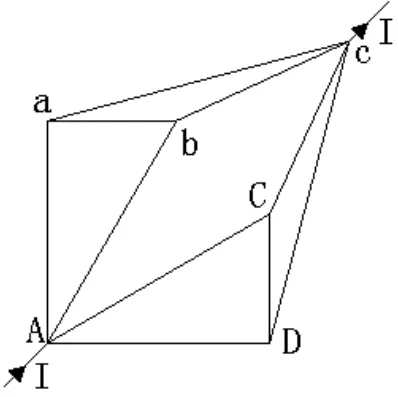
图4

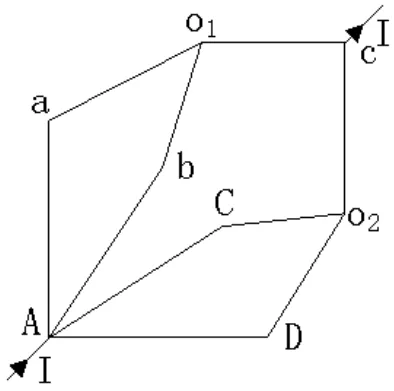
图5

2.3 实验法求解

对于一个复杂的无源线性二端网络，可以利用实验的方法求出其电阻。即利用伏安法求电阻或者利用直流电桥测出二端网络的电阻。本文不再赘述。

3 结语

本文主要利用欧姆定律和电阻的星（Υ）—三角（△）变换等不同的方法，求出一个正方体的每个棱都是一个电阻R时，这个正方体的对角顶点间的等效电阻，相互验证了方法的正确性，为特殊电路的分析计算找到新的方法。

参考资料

[1]谭永霞.电路分析[M].成都∶西南交通大学出版社,2004

[2]王慧玲.电路基础[M].北京∶高等教育出版社,2004

Calculating Resistance Method of Complex Network of Two-terminal

Zhang Hongbao

Special passive linear two-terminal network equivalent resistance calculating method. A cube each edge is a resistor R, how to find the resistance between the vertex angle on the cube? To solve this problem with the method of series-parallel will not work. In this paper, using the several different methods, Ohm’s law and resistance star(Υ)-Triangle(△) transformation , solved this problem , for circuit analysis and calculation to provide effective help.

two-terminal network; resistor; Ohm’s law;Υ-△transformation

Author’s address Dezhou Vocational and Technical College, Dezhou, Shandong,China 253034

TM13

B

1671-489X(2011)03-0077-02

10.3969/j.issn.1671-489X.2011.03.077

作者：张洪宝，副教授，学士，山东大学访问学者，主要从事电路分析、电机及应用等教学与研究工作。