基于葡萄糖代谢的大脑功能网络的小世界特性研究

【作 者】张方，张剑戈，左传涛，郭万华，王成＊

1 上海交通大学医学院生物医学工程教研室，上海，200025

2 复旦大学附属华山医院PET中心，上海，200235

3 南京大学附属鼓楼医院核医学科，南京，210008

大脑完成高级神经活动，例如认知、随意运动等，需要多个功能区域的协同工作。这一观点通过神经科学的实验已得到了证实。近年来，研究人员利用fMRI、EEG等设备进一步研究大脑的活动，特别是在静息状态下大脑的自发活动，通过分析不同脑区之间的相关性，建立了大脑的功能网络模型[1]。

大脑的功能网络特性的分析是当前神经影像学的研究热点。研究人员从图论出发，对大脑功能网络的路径长度、节点数等网络特性进行了分析，以图建立大脑工作的模型，揭示人脑思维的奥秘。Watts和 Strogatz[2]等人的研究认为，某些生物学网络和社会学网络的拓扑连接，既非完全规则，也非完全随机，并提出了小世界（small-world）模型。该模型具有类似规则网络的高度集群性，又像随机网络那样具有短的特征路径长度。Stephan[3]等人将小世界模型用于大脑功能网络的研究，他们通过对短尾猿的大脑皮层研究，证明了大脑皮层的功能连接含有小世界网络特性。He[4]等人测量了MRI图像中人脑皮层厚度，建立了不同个体间皮层厚度的连接网络，并证实了从大脑结构角度出发，其网络也具有小世界特性。Salvador[5]等人测量了静息状态下的BOLD信号值，并用图论对获得的fMRI数据进行了分析，包括提取了90个大脑皮层和子皮层区域，报告了整个大脑网络具有小世界特性的结果。

Latora和Marchiori提出用“效率”来衡量网络的高速信息转换，他们认为小世界网络同时兼有高的全局效率和局部效率，并在猕猴以及猫的大脑皮层神经网络中得到了证实。Sophie Achard[6]等人应用fMRI数据建立大脑功能网络，提出该网络具有经济的小世界特性，表现为网络的高效率和低成本。他们将实际大脑功能网络同相应的随机网络和规则网络进行比较，随机网络具有较规则网络更高的全局效率，而规则网络的局部效率则高于随机网络。具有小世界特性的网络满足条件：(1) 全局效率高于规则网络，低于随机网络；(2) 局部效率高于随机网络，低于规则网络。

能量的消耗是大脑功能活动的基础，研究表明大脑的能量消耗占人体全部消耗的20%[7]。18F-FDG PET成像信号与葡萄糖代谢有关，为分析大脑能量消耗提供了直接的证据。为了研究利用葡萄糖代谢指标所构成的功能网络，是否同样具有经济的小世界特性，本研究采用PET成像技术，通过分析和计算148个健康人的大脑皮层各个脑区的功能链接，建立大脑葡萄糖代谢功能网络，对大脑功能网络的成本和效率等特性进行分析。

1 研究对象及方法

1.1 研究对象

筛选2006年2月至2006年12月间在华山医院PET中心进行健康检查的正常人，共148人，年龄在30～59(47.1±7.7)岁之间，其中男性112人，女性36人。所有的入选者符合以下的条件: (1)既往无糖尿病病史；(2)既往无心肌梗死、心绞痛、高血压、心律失常、风湿性心脏病或其他心脏病史；(3)既往无脑卒中、短暂性脑缺血发作、癫痫、头痛、脑外伤、精神异常、痴呆等神经精神系统疾病史；(4)无长期乙醇(酒精) 或药物滥用史；(5)右利手；(6)学历初中文凭以上；(7)体格检查(包括视野、听力和语言功能等) 正常；(8)智能评分采用简易智能状态评分量表(MMSE)，总分在正常范围；(9)心率低于100次/min，血压收缩压＜ 140 mmHg，舒张压＜ 90 mmHg，空腹血糖＜ 6.0 mmol/L；(10)CT或MRI脑扫描未见明显异常。

1.2 PET显像

所有受试者的图像均采集自德国西门子公司的Biograph Sensation 16 PET/CT。显像剂采用18氟脱氧葡萄糖(18F-FDG，由华山医院PET中心合成和提供)，放射性化学纯度＞95%。静脉注射18F-FDG 10～15 mci，安静、避光情况下休息，于注射后30～45分钟进行PET/CT脑显像。

1.3 图像预处理

图像预处理采用SPM5对PET图像进行空间归一化。不同受试者的PET图像存在个体差异。应用SPM塑性形变的原理，将PET图像与Montreal Neruological Institute(MNI) PET标准模板进行匹配，实现空间归一化。图像经过重新采样，分辨率为2 mm×2 mm×2 mm。

1.4 脑区自动提取

应用Tzourio-Mazoyer[8]报道和验证的AAL大脑解剖标记模板，采用本研究小组开发的程序，对空间归一化后的PET图像进行脑区的提取。每一幅PET图像分别提取了90个解剖脑区(左右半脑各45个)。计算每一个脑区像素的灰度平均值作为该脑区的PET值，并使用全脑平均值进行归一化处理，以减少随机误差和个体差异。

1.5 建立脑区相关矩阵

在研究大脑网络的结构和特性之前，需先建立相关连接矩阵。根据Friston[9]对大脑功能性连接的定义，两个系统(脑区)之间的功能性连接可以定义为系统之间的相关性或者是协方差。本研究计算了148名观察者90个脑区PET值之间的Pearson相关系数，作为建立连接矩阵和研究功能连接性的基础。

通过计算两两脑区之间的相关系数，建立相关性矩阵(图1)。

图1 90个脑区间葡萄糖代谢的相关性Fig.1 The correlation of glucose metabolism of 90 brain regions

矩阵大小为90×90，即计算了90×89/2=4005对脑区的相关系数。图1中横坐标和纵坐标值分别是90个解剖脑区的编号[10,11]。图1中各区域由暗到亮代表了脑区间的相关性由弱到强，对应相关系数由小到大为0～1。区域越亮代表相关性越强；区域越暗代表脑区间的相关性越弱。

1.6 分析网络特性

1) 网络成本

大脑功能网络连接图G中，“节点”代表不同的脑区，“连接”代表脑区间的联系，网络节点数记为N，连接边数记为K[12]。为了分析大脑功能网络的特性，相关矩阵必须通过设定阈值来产生新的连接矩阵A={aij}。

若矩阵元素aij的值在阈值范围内则置1，表示节点i和j之间存在连接的边，超出阈值则置0。因此，每一个连接矩阵代表一个无权重的网络G，由N个节点和K条无方向的边组成，连接相应的非零元素。K与整个网络的最大可能存在的节点间的连接数量之比为网络成本(Cost)[6]：

2) 网络的全局效率、局部效率

在网络连接图G中，定义最短路径长度(shortest path lengths) dij是连通节点i与j的所有路径中，连接边数总和的最小值。

定义节点i与j之间连接的效率为eij，可以得到eij与节点i和j之间的最短路径长度dij成反比[12]，即

当节点i与j间无连接时，dij=+∞，相应的eij=0。当网络无权重时，dij为两节点间的最短物理距离Lij。

定义全局效率（global ef fi ciency）为[12]：

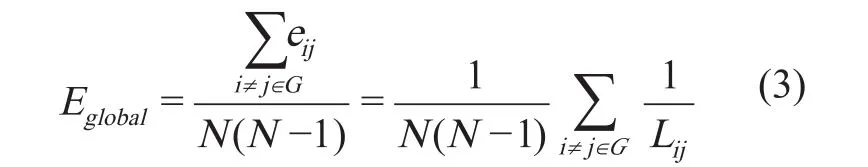
定义局部效率(local ef fi ciency)为[12]：

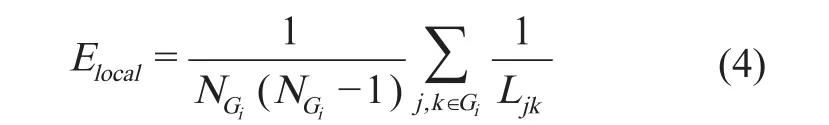
Gi定义为G的子网络，包含节点i及其连接点。式(4)中NGi是子网络Gi的节点数，局部平均效率是对子网络中每个节点的效率的平均。

3) 网络的成本效率

按照实际网络的节点数N和连接数K建立随机网络和规则网络，用于比较大脑功能网络G的全局效率和局部效率。

以网络的成本作为阈值，选取不同的网络成本(Cost)，网络的拓扑结构会产生较大的改变，将直接影响网络的执行效率。Sophie Achard[6]等人选取[0.01，0.5]的网络成本区间研究经济的大脑网络的效率。本文选取网络成本区间Cost～[0，1]，计算全局效率和局部效率随网络成本的变化情况，得到网络“全局效率—成本”曲线和“局部效率—成本”曲线。

当大脑功能网络的全局效率大于规则网络的全局效率，且小于随机网络的全局效率时，对应的网络成本区间范围定义为小世界区间(small world regime)[6]。

定义网络的成本效率(cost efficiency)为网络的全局效率与网络的成本之差[6]：

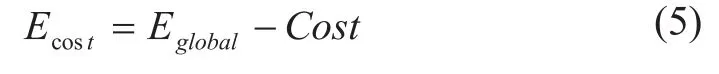
网络的成本效率（Ecost）随网络成本（Cost）的改变而改变，这一变化趋势可以由“成本效率”曲线来描述，本文同时分析了该曲线的特性。

1.7 计算不同年龄组的大脑网络特性

按照1 0岁为一个年龄段，将受试者分为三组：30～39(36.3±2.2)岁共48人，为A组；40～49(44.7±2.9)岁共50人，为B组；50～59(54.0±2.6)岁共50人，为C组。同样计算其网络的全局效率、局部效率，得到分组网络的“全局效率—成本”曲线和“局部效率—成本”曲线，分析不同年龄段的大脑功能网络是否体现小世界网络特性。

2 结果

2.1 大脑功能网络的小世界特性

通过对比大脑葡萄糖代谢网络和随机网络以及规则网络的全局效率和局部效率，得到148例样本整体的 “全局效率—成本”曲线(图2a)和“局部效率—成本”曲线(图2b)。其中横坐标为网络的成本(Cost)，纵坐标分别为网络的全局效率和局部效率。

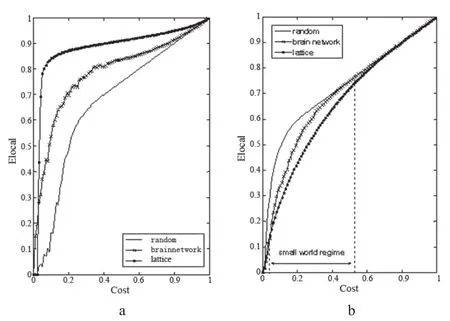
图2a 全局效率—成本曲线 图 2b 局部效率—成本曲线Fig.2a The global ef fi ciency-cost curves, Fig.2b The local ef fi ciency-cost curves

图2a中点线为规则网络的全局效率随网络成本变化的曲线，黑色实线为随机网络的全局效率曲线，叉线为分析葡萄代谢而得到的大脑功能网络的全局效率曲线。与图2a相似，图2b中点线为规则网络的局部效率曲线，黑色实线为随机网络的局部效率曲线，叉线为大脑功能网络的局部效率曲线。随机网络和规则网络都具有同实际大脑功能网络相同的节点数和连接数。由此可见，大脑功能网络的网络效率，包括全局效率Eglobal(图2a中叉线)和局部效率Elocal(图2b中叉线)，随网络成本(Cost)的增长而增长。大脑功能网络的小世界区间为Cost～[0.0512，0.5406]（图2a中虚线区间），在此区间内，大脑葡萄糖代谢网络的效率曲线介于随机网络和规则网络之间：大脑网络的全局效率比规则网络高，但低于随机网络；局部效率比随机网络高，低于规则网络。即平均有5%到54%对连接存在时(最大可能连接数为4005对)，大脑功能网络体现小世界特性。

图3 成本-效率曲线Fig.3 The cost-ef fi ciency curve

根据公式(5)得到148例样本整体的大脑功能网络 “成本效率”曲线(图3)，其中横坐标为网络的成本，纵坐标表示网络的效率。结果显示，大脑功能网络的全局效率Eglobal(图3中叉线)和局部效率Elocal(图3中点线)要高于大脑网络的成本(Cost)(图3中虚线)，符合高效率、低成本的小世界网络特性。在成本Cost=0.23时，网络的成本效率（Ecost）达到峰值，如图3中黑色实线所示，即用最小的成本达到最高的效率，此时经济的小世界网络特性体现最为显著。

2.2 不同年龄段大脑功能网络的小世界特性

进一步计算各个年龄段的全局效率和局部效率，并同相应的随机网络和规则网络进行比较，得到不同年龄段的“全局效率—成本”曲线（图4a）和“局部效率—成本”曲线（图4b）。

图4a 不同年龄段全局效率—成本曲线，图4b 不同年龄段局部效率—成本曲线Fig.4 a The global ef fi ciency-cost curves of different age groups,Fig.4 b The local ef fi ciency-cost curves of different age groups

图4a中，细虚线、点线、叉线分别为A组、B组、C组实际大脑功能网络的全局效率曲线；A组、B组、C组大脑功能网络的局部效率曲线分别对应图4b中细虚线、点线和叉线。结果显示，各年龄组“全局效率—成本”曲线和“局部效率—成本”曲线同样本整体样本的结果曲线相似，均介于随机网络和规则网络之间，体现出经济的小世界网络特性。具有小世界特性的成本区间分别为，A组[0.0612～0.4307]，B组[0.0412～0.4407]，C组[0.0312～0.4107]。因此，不同年龄的大脑葡萄糖代谢功能网络都具有经济的小世界特性。

3 讨论

本研究以18F-FDG PET图像为基础，建立了基于葡萄糖代谢的大脑功能网络，对网络效率和成本等特性进行了分析。结果显示，在网络中低成本区间内，大脑功能网络的全局效率和局部效率处于相应的随机网络和规则网络之间，从网络效率的角度证明18FFDG PET大脑功能网络具有小世界特性。这一特性，在样本的整体以及不同年龄的样本组中都得到了验证。Sophie Achard[6]等人的研究报道的基于fMRI的大脑功能网络小世界区间为[0.05～0.34]，本研究得到小世界成本区间为[0.0512，0.5406]。与之相比，基于葡萄糖代谢的大脑功能网络的小世界区间更大，网络的小世界特性更为显著。

因此，基于葡萄糖代谢的大脑功能网络具有高效、低成本的小世界特性。但年龄、性别等对大脑功能网络小世界特性的影响作用还需要进一步的研究。利用18F -FDG PET图像得到的静息状态的大脑葡萄糖代谢连接网络，可以有效地应用于大脑功能的研究。

[1] Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems[J]. Nature Review Neuroscience, 2009, 10 (3):186-198.

[2] Watts DJ, Strogatz SH. Collective dynamics of 'small-world'networks[J]. Nature, 1998, 393 (6684):440-442 .

[3] Stephan KE, Higetagcc, Burns GA, et al. Computational analysis of functional connectivity between areas of primate cerebral cortex[J].Philosophical Transactions of the Royal Society of London Series B-Biological Sciences, 2000, 355 (1393):111-126.

[4] He Y, Chen ZJ, Evans A C. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI[J]. Cerebral Cortex, 2007, 17 (10):2407-2419 .

[5] Salvador R, Suckling J, coleman MR, et al. Neurophysiological architecture of functional magnetic resonance images of human brain[J]. Cerebral Cortex, 2005, 15 (9):1332-1342 .

[6] Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. Plos Computational Biology[J], 2007, 3(2):174-183.

[7] Fox M D, Raichle M.E. Spontaneous fl uctuations in brain activity observed with functional magnetic resonance imaging[J]. Nat Rev Neurosci, 2007, 8 (9):700-711.

[8] Tzourio-Mazoyer N, Landean B, Papathanssion D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J].Neuroimage, 2002, 15 (1):273-289.

[9] Friston KJ, Frith CD, Fletcher P, et al. Functional topography:multidimensional scaling and functional connectivity in the brain[J]. Cereb Cortex, 1996, 6 (2):156-164.

[10]张剑戈, 张方, 黄喆慜, 等. 海马区脑功能连接网络随年龄变化的研究[J]. 中华核医学, 2009, 29 (6):391-394.

[11]Zhang Jiange, Zhang Fang, Da Xiao, et al. The method based on functional connectivity for the analysis of age effects on hippocampus[C]. The 3rd International Conference on Bioinformatics and Biomedical Engineering(ICBBE’09)Jun,2009

[12]Latora V, Marchiori M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 8719 (19): 198701.