虚时间步长法的狄拉克海难

李芳琼，蔡立

（贵州民族学院，贵州贵阳550025）

虚时间步长法(ITS)[1]是用于寻找最快的能量减少方向,沿着这个方向迭代直到找到能量曲面的极小点,这种方法是在坐标空间中解决非相对论问题的一种有效方法,而且在常规的平均场理论中得到了成功的应用[2]。正如文献[1]所指出的一样,由于经过几次指数变换,只能得到最低的本征态,这个方法被应用于求解能谱从底部开始束缚的单粒子哈密顿量。

从物理的角度来讲,科学家们在奇特原子核中[3]发现了许多新奇的核结构现象以及完全预想不到的核结构特征。奇特核中极端丰中子的特征和与低物质密度分布相关的物理现象不仅引起了核物理学、天体物理学界的关注,而且还对在坐标空间中求解复杂的多体问题提出了新的挑战。

在过去的几十年中,作为描述奇特原子核最好的理论方法之一即相对论平均场(RMF)方法[4]在描述许多原子核的现象时取得了很大的成功[5]。其后,RCHB理 论[6]提供了一种处理包括连续谱在内的对关联的完全自洽的方法,因此对远离β稳定线的原子核提供了可靠的描述,而且较好的再现实验上观测到的11Li晕现象。RCHB理论的推广是对变形的奇特原子核的探索以及确定变形晕的存在。在这方面已经有了很多的研究。由于在坐标空间中求解形变体系的耦合道微分方程存在很大的困难[7],Woods-Saxon基展开的方法被提出[8],但是它在重原子核系统中的应用却非常耗时。

对ITS方法,从球形到形变系统的扩展是很直接的,然而由于Dirac海的存在,ITS方法是否可以直接应用于相对论系统,仍然是一个有趣的问题。虽然通过将上分量满足的有效哈密顿量应用于现有的Skyrme-Hartree-Fock方法中的ITS程序,人们已经得到了Fermi海中的单粒子能级[9]。但是为了证明这个方法的可行性、可靠性,以及明确的理解它对Dirac海的影响,还有很多的工作需要去做。

在本论文中,ITS方法将用在坐标空间中求解Dirac方程。文中将分析并详细讨论将ITS方法直接应用在Dirac方程时所遭遇的Dirac海难,并且通过比较Dirac方程和等效的Schrdinger-like方程,提出了避免Dirac海难的确实可行的办法。

1 理论框架

ITS方法的主要思想和详细的公式体系参见文献[1]。单粒子波函数的ITS演化可表示为

其中,这里指数级数变换的展开只保留到一阶,与文献[2]类似。为单粒子的哈密顿量,是在时刻的一组相互正交的单粒子波函数。正交化由(1)得到的产生一组新的正交波函数,用于下一次的ITS演化。随着时间的演化,系统的总能量下降,直到找到能量曲面的极小点。相应的波函数将同时收敛到单粒子哈密顿量的本征态。

ITS方法在常规的平均场理论中已经得到了很成功的应用。对于相对论平均场的情况,主要的问题就是求解Dirac方程,

这里和是标量势和矢量势。为了更清楚而简单的说明,这里的取为球形的Woods-Saxon势的形式,与文献[8]类似。那么Dirac旋量可以写成如下形式:

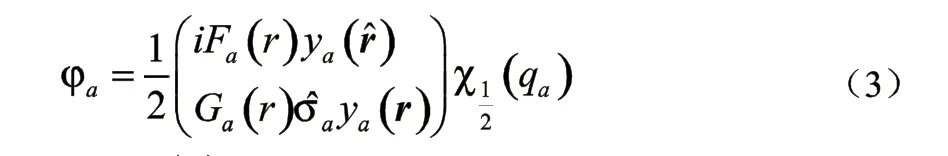
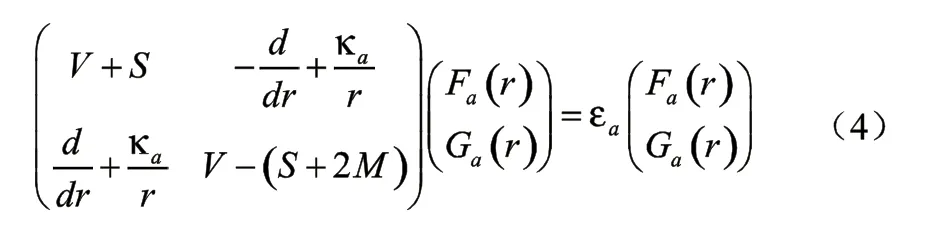
由于ITS方法搜寻的是从正无穷延伸到负无穷的Dirac方程全部能谱中能量的最低状态,如果把(4)式左边的2×2矩阵的单粒子的哈密顿算符直接用于ITS演化(1)式,那么,所有的单粒子能级将掉进Dirac海中,从而在Fermi海中得不到物理解。因此,将ITS方法直接演化Dirac方程会遇到巨大的灾难,因此有物理意义的解完全被负能态所淹没,或者叫Dirac海难。

为了避免Dirac海难一种可能的解决办法就是用ITS方法去演化Schrdinger-like方程,而不是Dirac方程。直观的来看,这种可能性也是值得怀疑的,因为Schrdinger-like方程是从Dirac方程中导出,并且由于所有的Dirac方程的解都满足相应的Schrdingerlike方程,这两种方程实际上是完全等价的。

在下面的讨论中,可以看出这两种方程在ITS演化过程中其实是不等价的。

由方程(4)可以得到波函数的上分量和下分量的关系：

Dirac方程和等效的Schrdinger-like方程的区别由此显现出来。对Dirac方程来说,单粒子能谱从正无穷延伸到负无穷。但对Schrdinger-like来说,尽管(6)式中包含着单粒子能量的有效哈密顿量非常复杂,但它可以被约化为如果尝试的单粒子能量被设置在Fermi海中,那么恒正的有效质量会保证,因此Fermi海中的单粒子能谱就可以与Dirac海中单粒子能谱分离开来,那么ITS的演化就可以应用于Schrdinger-like方程,从而获得在Fermi海上的解。另外为了获得Dirac海里的解,我们应用类似的方法去演化电荷共轭变换后的Schrdinger-like方程[10]。因此正是这种从Dirac方程到Schrdinger-like方程的变换,容许了分别在Fermi海或Dirac海中的单粒子能谱的ITS演化,从而提供了避免Dirac海难的方法。

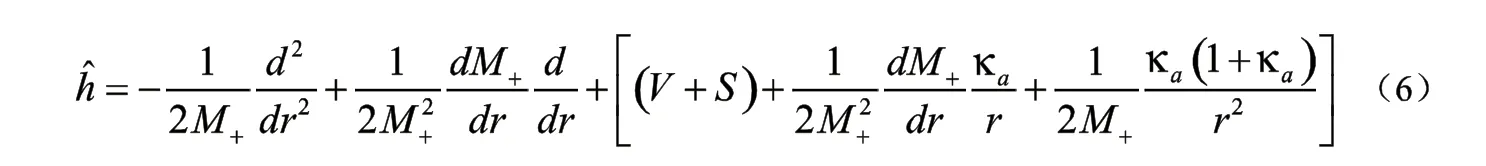
利用(6)式有效的哈密顿量,波函数的上分量由Schrdinger-like方程的ITS演化获得。而对应的下分量可以通过(5)式获得。然后包括上、下分量的Dirac旋量经过正交化后进行下一次的迭代。

2 结果与讨论

通过对12C、16O、132Sn、208Pb单粒子能级的ITS演化,都得到了相同的结论。以下以12C为例。

图1给出的是用ITS演化Schrdinger-like而获得的12C在Dirac海中的质子的2f(第一行)和2g(第二行)自旋伙伴态的径向波函数和相应的单粒子能量,与shooting方法得到的精确解完全相同。演化的盒子边界R=20fm,格点间距dr=0.1fm,时间步长dt=10-27s。

图2给出的是用ITS演化Schrdinger-like方程而获得的在Fermi海和Dirac海中的12C单质子能级。ITS演化的球形盒子边界为R=20fm,格点间距dr=0.1 fm,时间步长为Δt=1×10-27s.所获得的单质子能级与用相同盒子大小的shooting方法所得到的“精确解”是一样的。自旋伙伴态成对出现,其中左侧(右侧)κ>0(κ<0)。值得注意的是所有的单粒子态全部用上分量的量子数来标记,与文献[10]相似。因此这很清楚的表明,通过ITS方法演化等效的Schrdingerlike方程可以避免Dirac海难。

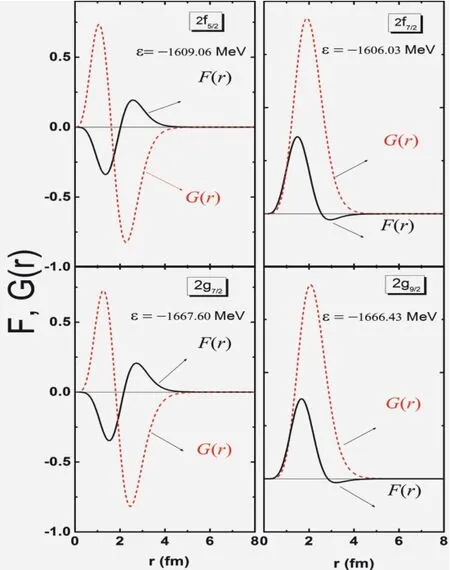
图1 用ITS演化Schrdinger-like获得12C在Dirac海中质子的2f第一行)和2g(第二行)自旋伙伴态的径向波函数和单粒子能量

图2 应用ITS演化Schrdinger-like方程,避免了Dirac海难,得到12C在Fermi海以及Dirac海 中质子的分离的单粒子能谱

综上所述,通过用虚时间步长方法(ITS)演化Schrdinger-like方程得到了Fermi海和Dirac海中分离的单粒子能谱,避免了出现Dirac海难。

3 结论

ITS方法在常规的平均场理论中得到了广泛的应用,但是当它直接应用于Dirac方程时,不可避免的要遇到一个严峻的挑战。所有的单粒子能级将会演化到Dirac海中,Dirac方程的物理解被Dirac海所淹没。然而从Dirac方程导出的Schrdinger-like方程提供了避免Dirac海难的方法。在比较长的时间里,Schrdinger-like方程被认为与Dirac方程是完全等价的。然而,通过将Dirac方程转化为等效的Schrdingerlike方程,从正无穷延伸到负无穷的单粒子能谱可以分别在Fermi海或Dirac海中通过ITS演化而获得。ITS方法演化Schrdinger-like方程或电荷共轭的Schrdinger-like方程,将得到在Fermi海或Dirac海中的解,它和用shooting方法得到精确解完全一致。用ITS方法在相对论平均场中对12C进行自洽的计算所获得的结果和用shooting方法完全一致。本文中对ITS方法的成功应用,充分证明了该方法用于描述相对论系统的可行性、实用性、可靠性。

[1] DaviesKTR,FlocardH,KriegerS,etal.Application of the imaginarytimestepme thodt otheso lutionofthe static Hartree-Fockproblem[J].NuclPhysA,1980,(342):111-123.

[2] BoncheP,FlocardH,HeenenPH.SolutionoftheSkyrme HF+BCSequationona3Dmesh[J].ComPhysCom,2005,(171):49-62.

[3]JensenAS,RiisagerK,FedorovDV,etal.Structure and reactionsofquantumhalos[J].RevModPhys,2004,(76):215-261.

[4] SerotBD,WaleckaJD.Therelativisticnuclearmany-body problem[J].AdvNuclPhys,1986,(16):1-327.

[5] MengJ,TokiH,ZhouSG,etal.Relativisitccon tinuum HartreeBogoliu bovtheory forground-statepr opertiesof exoticnuclei[J].ProgPartNuclPhys,2006,(57):470-563.

[6] MengJ,RingP.RelativisticHartree-Bogoliubov Description oftheNeutronHaloin11Li[J].PhysRevLett,1996,(77):3963-3966.

[7] PriceCE,WalkerGE.Self-consistent Hartree description of deformednucleiina relativistic quantumfieldt heory[J].Phys RevC,1987,(36):354-364.

[8] ZhouSG,MengJ,RingP.Sphericalr elativist icHartree theoryina Woods-Saxonbasis[J].PhysRevC,2003,(68):034323.

[9] GgeleinP,MtherH.Nuclear Matterin the Crust of Neu-tron Stars[J].Phys.Rev.C2007,(76):024312.

[10] LiFQ,ZhangY,MengJ.Convergence for ImaginaryTime Step Evolutionin the Fermiand Diracseas[J].SciChinaSer G,2010,(53):327-330.