基于MATLAB的某火炮制退机反面分析计算

高 颖，杨 臻，王瑞龙，吴其军

（1.中北大学 机电工程学院，太原 030051；2.中国兵器工业208研究所，北京 100081）

0 引言

制退机又称驻退机。它在发射过程中，产生一定规律的阻力用于消耗后坐能量，将后坐运动限制在规定的长度内，并控制后坐和复进运动的规律。制退机的工作原理是利用液体经过小孔流动时产生的阻尼，使得制退机的活塞两端产生压力差。这种压力差作用到活塞上即形成制止后坐运动的阻力，通常成为液压阻力，液体通过的小孔称为流液孔。流液孔的面积可决定液压阻力的大小。因此，知道制退机流液孔的变化规律，即可调节制退机的液压阻力，进而实现要求的后坐阻力规律。

图1 制退机结构简图

制退机的几个主要尺寸包括：制退机的工作长度L，制退机的内径Dr，制退杆外径dr，制退杆内腔直径d1，节制环直径dp和节制杆外形尺寸等。

在反后坐装置设计计算中，有正面问题计算和反面问题计算两类问题。正面问题是指在正常设计条件下对确定后坐阻力规律确定制退机的结构尺寸及流液孔的变化规律；在反面问题计算时，由于火炮的结构尺寸和制退机的结构已经确定已知制退机结构尺寸下求解实际运动诸元及制退机液压阻力的变化规律。在制退机正面计算后，进行反面问题的计算，可以检验设计的合理性，随着计算机技术的发展，反面问题计算已经成为火炮射击时的受力和运动规律的一种预测手段。

火炮反后坐过程中涉及到火药气体燃烧，液流阻力等复杂过程，某些参量只能是时间或后坐行程的离散函数，故不能采用解析解法，只能采用数值积分的方法。在相当长的一段时间内，火炮反后坐装置反面计算采用的方法比较随意性，有二次近似法，梯形近似积分方法，也有一些借助计算机的四阶RUNGE-KUTTA法，这些方法普遍精度低，效率不高，缺乏对求解精度的讨论和控制。

MATLAB是当前数值计算中比较流行的软件，提供了许多比较先进的数值计算方法。它包括大量计算算法的集合，可以方便地实现用户所需的各种计算功能。函数中所使用的算法都是科研和工程计算中的最新研究成果，利用MATLAB中的先进、高效地微分方程求解器，编制反面计算的设计程序，大大提高了计算精度和计算效率。本文将MATLAB用于某型火炮反后坐设计反面问题的计算，结果证明了这种做法的可行性与有效性。

1 火炮反后坐装置设计反面计算的基本方程

制退后坐运动方程为

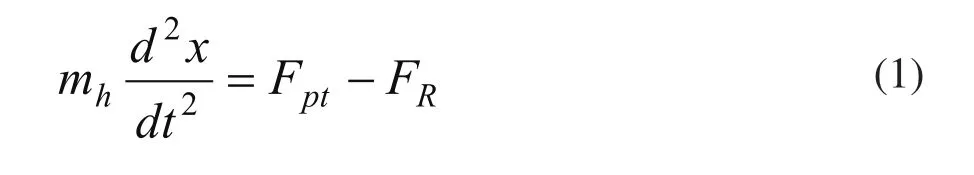
可写为微分方程的标准形式

即有

或

其中，y1=x，y2=v。

求解常微分数值方法可用Runge-Kutta方法。四阶Runge-Kutta公式为

其中

2 MATLAB编制反面计算程序

Runge-kutta方法是最通用的常微分方程求解方法。就求解微分方程而言，MATLAB提供了多种高效的求解器，包括求解非刚性连续方程的ode45（显式四级五阶Runge-kutta法）、ode23(显式二级三阶Runge-kutta法)、ode113(变阶Admas-Bashforth-Moultou法)和求解刚性连续方程ode15s、ode23s、ode23t等，这些基本都是变步长求解法，有着很高的精度。

在微分方程的求解问题上，任何一种求解器都不是万能的，用MATLAB编制程序可以选择不同的方法和不同的参数求解微分方程，用户可以根据详细的帮助文档选择合适的求解器以及确定求解器的参数，在精度、稳定性和效率等方面做到最佳的平衡，以保证火炮制退机的反面分析计算可以得到较精确的结果。

用MATLAB编制反面问题的计算程序，在火炮的结构尺寸和制退机的结构已经确定的条件下，求解后坐运动诸元、后坐阻力及制退机的液压阻力等随时间变化的规律。后坐反面问题程序框图如图2所示。

图2 后坐反面问题程序框图

3 反面计算求解

依据后坐反面计算的基本方程及其他参量函数的计算方程编制计算程序，采用主函数调用子函数缺省求解，得到后坐运动诸元、制退机液压阻力随后坐时间及后坐行程的变化规律。

图3 正面计算中后坐速度-行程曲线图

图4 反面计算中后坐速度-行程曲线图

图5 正面计算中后坐阻力-时间曲线图

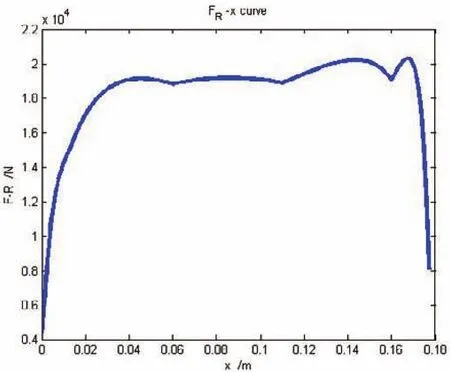
图6 反面计算中后坐阻力-时间曲线图

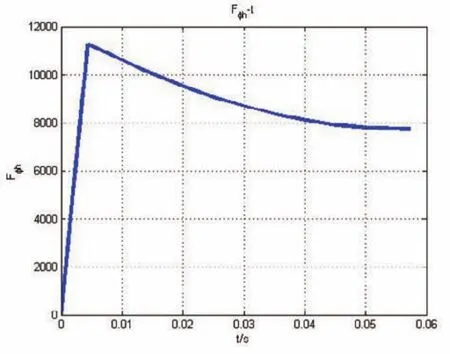
图7 正面计算中制退机液压阻力-时间图

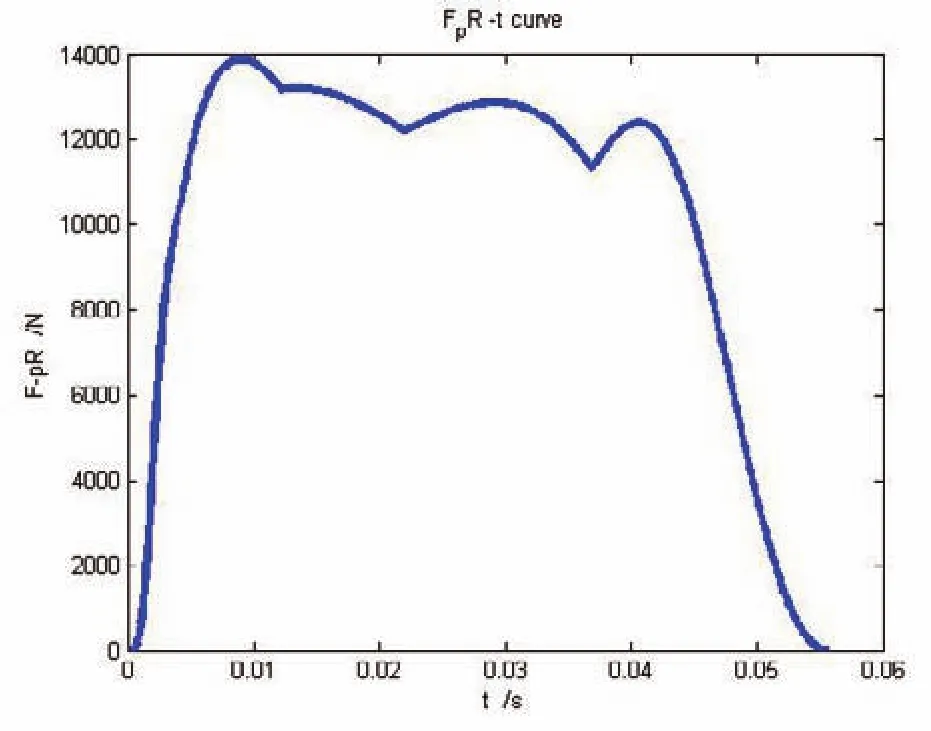
图8 反面计算中制退机液压阻力-时间图

由上图可知，反面计算的结果曲线图和面设计计算的结果曲线图大体上走向是一致的，曲线图大体上比较吻合。但是由于实际中各种复杂因素的影响，导致了其规律变化性较大，不一致的地方也正好说明了正面设计中存在的一些问题还需要改进，如某些液压阻力参数的选取不合适，节制杆调整后直径不合理等，后坐阻力和后坐诸元并不是像正面计算中很有规律的变化，经与实际的制退机工作情况比较，反面计算和实际情况比较吻合。在火炮制退机的设计过程中，可以在反面分析计算的结论下可以改进一些结构尺寸进而重新计算，直到达到比较理想的结果，由此可见反面计算精确性的重要性。

4 结论

MATLAB作为目前世界上最有影响力的数值计算软件，将其应用于传统的火炮行业，进行了反后坐装置的反面计算，大大地提高了计算精度和计算效率，将其计算得出的结果与正面计算的结果比较，有效地检验了设计的合理性，这种方法可以在设计的过程中及早地发现正面设计中存在的一些问题，进而预先改进，大大地减少了研发时间和降低了研发费用。本文的工作是这方面的一个尝试。

[1]张月林,等.火炮反后坐装置设计[M].北京:国防工业出版社,1984.

[2]谈乐斌,等.火炮概论[M].北京:北京理工大学出版社,2005.

[3]高树滋,陈云生,张月林,郑建国.火炮反后坐装置设计[M].北京:兵器工业出版社,1995.

[4]王正林,等.精通MATLAB科学计算[M].北京:电子工业出版社,2009.

[5]刘维,等.精通MATLAB与C/C++混合程序设计[M].北京:北京航空航天大学出版社,2008.